Appropriate for Advanced Non-Experts
[This is the seventh post in a series that begins here.]
In the last post in this series, I pointed out that there’s a lot about quantum field theory [the general case] that we don’t understand. In particular there are many specific quantum field theories whose behavior we cannot calculate, and others whose existence we’re only partly sure of, since we can’t even write down equations for them. And I concluded with the remark that part of the reason we know about this last case is due to “supersymmetry”.
What’s the role of supersymmetry here? Most of the time you read about supersymmetry in the press, and on this website, it’s about the possible role of supersymmetry in addressing the naturalness problem of the Standard Model [which overlaps with and is almost identical to the hierarchy problem.] But actually (and I speak from personal experience here) one of the most powerful uses of supersymmetry has nothing to do with the naturalness problem at all.
The point is that quantum field theories that have supersymmetry are mathematically simpler than those that don’t. For certain physical questions — not all questions, by any means, but for some of the most interesting ones — it is sometimes possible to solve their equations exactly. And this makes it possible to learn far more about these quantum field theories than about their non-supersymmetric cousins.
Who cares? you might ask. Since supersymmetry isn’t part of the real world in our experiments, it seems of no use to study supersymmetric quantum field theories.
But that view would be deeply naive. It’s naive for three reasons.
1. Supersymmetric quantum field theories might be directly important in the real world. We don’t know that the world isn’t supersymmetric at shorter distances and higher energies than we can currently measure. We need to be able to calculate properties of supersymmetric quantum field theories so that we could recognize them for what they are, should experiments someday give us evidence for them.
2. Supersymmetric quantum field theories can give us analogies for aspects of the real world that we know about but don’t understand very well. The imaginary worlds that are described by certain supersymmetric quantum field theories sometimes bear a certain resemblance to the real world. Consequently it is sometimes possible to gain insights into the real world by studying these imaginary worlds… remembering that our understanding of the Standard Model is imperfect, because of the difficulty of working with its equations.
3. Supersymmetry enables us to discover entirely new features of quantum field theory that we did not know about, and that might be true of some non-supersymmetric theories too — and these too could be part of the real world. Remember the structure and features of the Standard Model, a rather complicated theory with many loose ends, still poses many puzzles for particle physicists. We don’t understand the number or strengths of the forces; we don’t understand why the particles come in the number they do and why their masses have the pattern that we observe; and there is the naturalness problem, among others. The imaginary worlds that are described by supersymmetric quantum field theories have a variety of interesting general features. Although supersymmetry was useful in making it possible for us to discover those features, some of those features are probably also true of non-supersymmetric quantum field theories for which we can’t calculate anything. So any one of these features might be an as-yet unknown aspect of the real world, even if the real world does not have supersymmetry at all.
So let me tell you a little about supersymmetry.
Supersymmetry: Some Basics
In a world with three spatial dimensions like ours, supersymmetric quantum field theory comes in three varieties
- maximal supersymmetry
- half-maximal supersymmetry
- minimal supersymmetry
Technically these are called N=4, N=2 and N=1 supersymmetry. [There’s no N=3 because consistency requirements turn it back into N=4. Supergravity can go up to N=8, but that’s another story. With more or fewer spatial dimensions, the details are different.] These were discovered in the 1970s.
The more supersymmetry a quantum field theory has, the simpler the required mathematics becomes, and the more things about the quantum field theory that can be calculated. The calculations in question aren’t done using methods that I’ve described so far (successive approximation and computer simulation); they’re done using fancier mathematics that takes full advantage of the simpler equations. [For non-supersymmetric theories, no known fancy math can be used; we may well need even fancier mathematics that hasn’t yet been invented, but at this point we’re almost powerless.]
However, the more supersymmetry a quantum field theory has, the more remote it becomes from the real world. As I mentioned, the real world might have minimal supersymmetry, hidden from us but actually present, though so far that hasn’t been discovered to be the case. It is unlikely (but not impossible) that some form of half-maximal or maximal supersymmetry has a partial, complicated and subtle role to play in the real world, but that’s a much more complex issue than I want to cover here. Let’s just say that maximal supersymmetry has no simple and direct possible role in the real world, whereas minimal supersymmetry may perhaps have such a role.
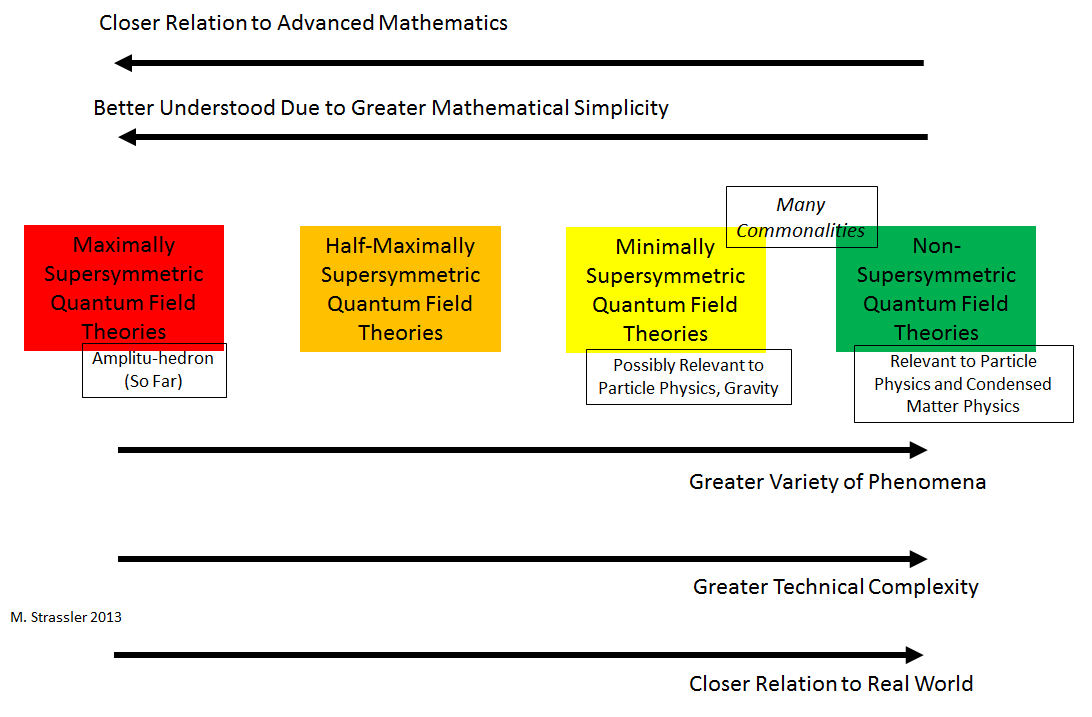
Yet maximal and half-maximal supersymmetric quantum field theories have proven very useful in learning about the real world. And they’ve proven extremely useful in learning about minimal supersymmetric quantum field theories, which in turn (a) might be directly relevant in the real world, and (b) have been somewhat useful in learning about non-supersymmetric quantum field theories, which are definitely relevant in the real world.
So what kind of things can we gain from supersymmetry?
Learning Lessons From Supersymmetry
1) Supersymmetry has made it easier to make particle physics predictions in non-supersymmetric theories.
In supersymmetric theories, the method of successive approximation (or “perturbation theory”, in jargonese) is simpler. It turns out that one of the best ways to do successive approximation in the Standard Model — a somewhat complicated non-supersymmetric quantum field theory (QFT) — is
a) do a similar calculation in a maximally supersymmetric QFT
b) do a similar calculation in a minimally supersymmetric QFT
c) do a similar calculation in a simple non-supersymmetric QFT
d) add them up, with appropriate care
More generally, the structure of calculations in non-supersymmetric theories can be broken up into parts that already appear in supersymmetric theories (and these are relatively easy to calculate) and parts that are special to the non-supersymmetric case (which can be studied in the simplest possible contexts.) In short, supersymmetry gives us a useful way of organizing our real-world calculations, so that the simple parts are separated out and done first, and then the small number of hard parts can be focused on.
This is also the logic and strategy behind the now-(in)famous “amplitu-hedron” method that received a very enthusiastic press article recently. The article was certainly over the top — and the title, “A Jewel at the Heart of Physics”, was a bit misleading. It should have been entitled “A Jewel at the Heart of Maximally Supersymmetric Physics”, since — so far — the details have been most clear for maximal supersymmetric quantum field theories, which have very special features and are far from the real world. But, as I said above, understanding the maximally supersymmetric case can be step one, with minimally supersymmetric theories to come next, and non-supersymmetric ones to come last but not least. So it’s early days for the amplitu-hedron, and too early to declare joy and rapture as loudly as did the press article about it all, but there is good reason for cautious optimism that these breakthroughs in maximally supersymmetric contexts will affect calculations in the real world within the next decade.
2) Supersymmetry has taught us that the effective field theory that describes the low-energy and long-distance behavior of a quantum field theory can have features which we’ve not encountered — yet — in the real world.
In a previous post I emphasized that in the strong nuclear force, the effective field theory for the low-mass hadrons (pions and kaons) is a useful tool, but that its form had to be guessed — we can’t, even today, determine the equations for the effective quantum field theory from the quantum field theory of the strong nuclear force. The only way to figure out the right theory is to guess it starting from data. Well, in supersymmetric quantum field theories, using methods developed in the 90s (which in turn were founded on earlier work from the 80s), we often can determine the right effective quantum field theory to a greater or lesser degree, starting with the equations of the original theory! There’s still often some guesswork involved, but the math often provides the clues we need.
For instance, take the imaginary world that we use for calculation of the strong nuclear force, with three low-mass quarks and eight gluons, carrying three types of color) The supersymmetric version of this world (see Figure 2) has a superpartner particles for the quarks and for the gluons. And at long-distance and low-energy, it has pion-like and proton-like hadrons, for which an effective quantum field theory can be written down. The power of supersymmetry opens up the door to an understanding of many features of these theories, not just the ones I’ve mentioned here.
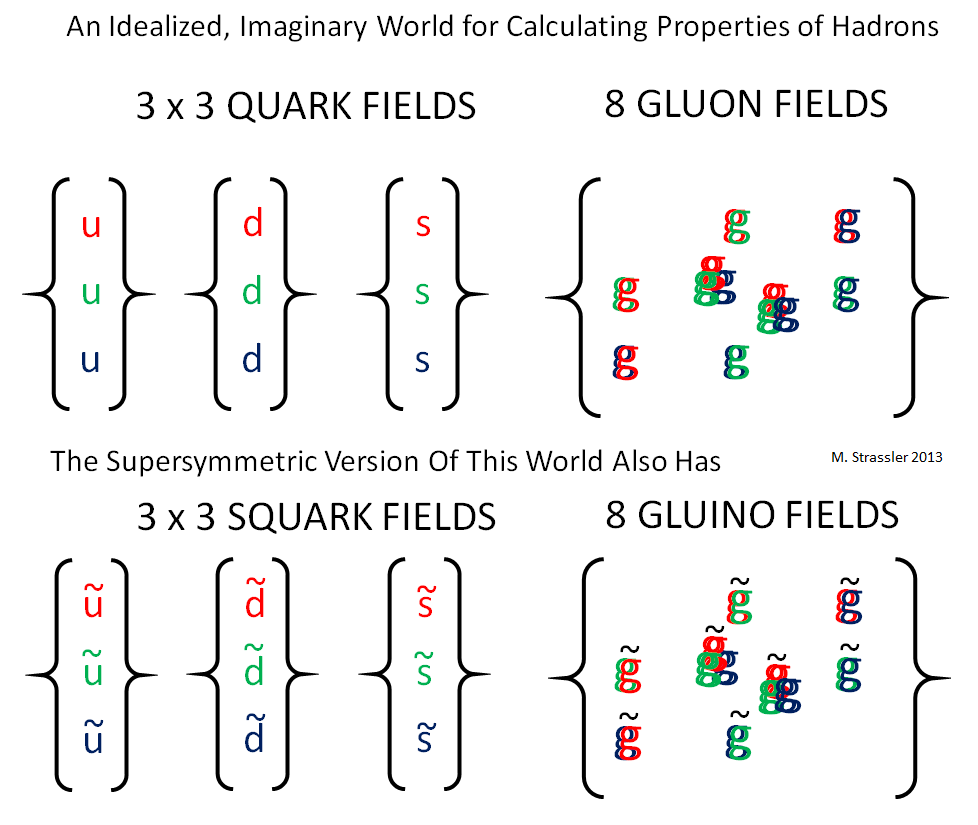
And in the process of learning how to do this, we also learned that quantum field theory can do many things that we didn’t previously know it could do. The initial wave of major discoveries about this were launched by the work in 1994 of Seiberg and Witten for half-maximal and maximal supersymmetric QFTs, and of Seiberg in minimal supersymmetric QFTs. I can tell you from having been there when it all was happening — these were heady days, where major insights into what quantum field theory was capable of were appearing every few weeks. [And then string theory got into the act, but that’s another story.]
For instance, we learned that the low-energy physics of a quantum field theory can involve gluon-like and quark-like particles that are neither some of the quarks and gluons of the original theory, nor made in a simple sense out of the quarks and gluons of the original theory. (This is in contrast to protons of the real world, which we understand as being made directly out of quarks and gluons.) They are, so to speak, “emergent”, arising in a complex and subtle way that even today we don’t entirely understand. See point (4) below.
By the way, curiously, computer simulations, such as are used for understanding the strong nuclear force, are not useful here! Supersymmetry is a complete disaster for computer simulations; the methods we have for simulating quantum field theories using computers do not work at all in the presence of supersymmetry. This is a very frustrating situation, but no one, despite years of work (and some very, very clever ideas) has yet crossed this barrier.
3) Study of supersymmetric quantum field theories has taught us that scale-invariant quantum field theories are far more common than we previously thought.
Thanks to the work of Seiberg, considerable evidence was obtained in the mid-90s that even for minimal supersymmetry, scale-invariant quantum field theories are very common. (A few such theories were known in the 70s, and more in the 80s, but they weren’t considered typical.) For instance, I emphasized that we have no idea how a quantum field theory like the real-world strong nuclear force, but with, say, 8 types of low-mass quarks, behaves when the forces become truly strong. Well, the supersymmetric version of this theory — with gluons and their superpartner particles (gluinos), along with 8 massless types of quarks and their superpartner particles (squarks) — turns out to be a scale-invariant theory at long distance. The supersymmetric version of the theory with a half-sextet and 7 half-quarks, is also scale-invariant, as we learned from Seiberg’s student Pouliot. Many properties of these theories can be calculated.
Today, thanks to these insights, it is widely believed that even non-supersymmetric scale-invariant quantum field theories are very common. This belief has motivated people to study the question using computers, and though the jury is still out, some evidence has already been obtained.
4) Often, two quantum field theories with entirely different fields are actually the same — sometimes exactly the same, and other times having the same long-distance low-energy behavior.
This phenomenon, known often as “duality” (but be careful, because the word “duality” is heavily over-used, and means different things in different contexts, even within physics), is one that deserves its own article. But suffice it to say that two (and sometimes more) quantum field theories, with entirely different sets of fields and entirely different equations, can sometimes have identical physical phenomena — depending on context, this may mean “exactly identical” or “identical only for low-energy and long-distance behavior”. Famous names associated with these developments, which go back to the 70s but became clear and widespread in the 90s, are Olive, Montonen, Sen, Seiberg, Witten; less famous names include yours truly and many others.
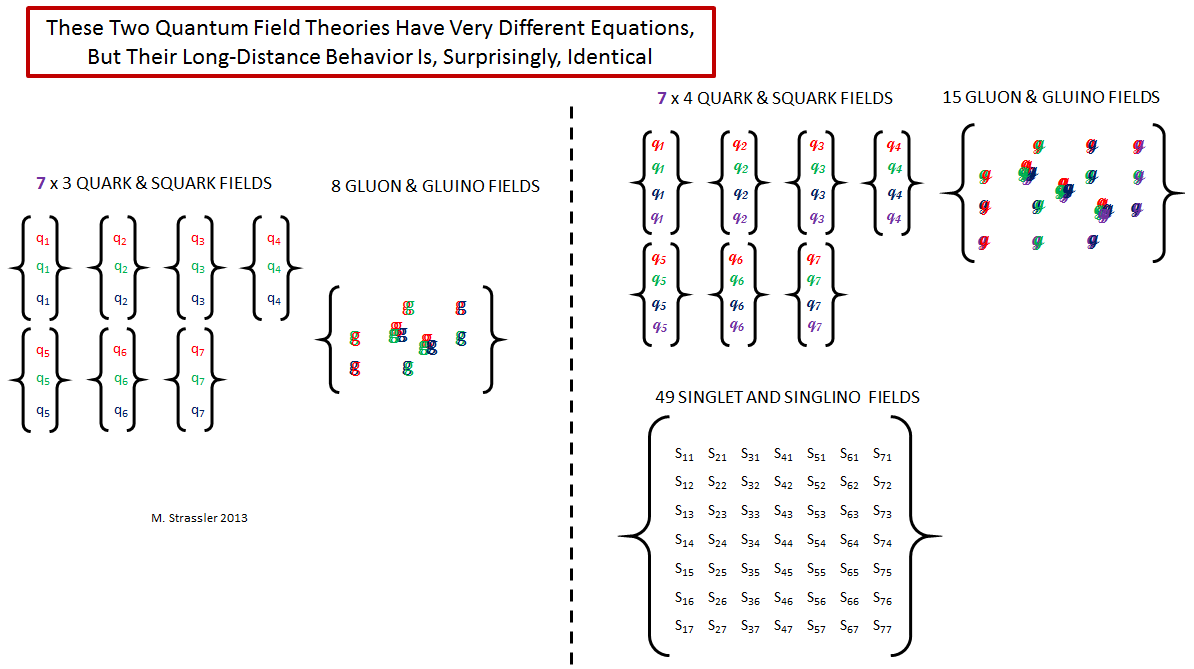
In fact, this is a grand generalization of the notion of effective field theories. An effective field theory is a quantum field theory whose equations may be used to describe the low-energy and long-distance phenomena of another quantum field theory. As occurs in the case of the strong nuclear force, the original theory and the effective field theory may have completely different fields and equations. For the strong nuclear force, the “original” theory is the theory of quark and gluon fields; the effective theory is a theory of pion and kaon fields, which describe the hadrons made from quarks and gluons. But the more general notion of duality is somewhat mind-blowing. Rather than the second set of fields being made out of the first set in the way a house is made from bricks, as for hadrons and quarks, it may happen that neither set of fields is made from the other in any simple-to-describe way.
5) Supersymmetry has allowed us to learn that there are quantum field theories for which no normal-looking equations can be written.
While using fancy mathematics to explore the various quantum field theories with half-maximal and minimal supersymmetry, some of my colleagues (initially Philip Argyres and Michael Douglas, but many more followed) came across theories whose properties simply aren’t consistent with any type of equations that we know how to write down.
Some clever trickery is required to find these things. In supersymmetric contexts, sometimes it is easier to figure out the answers to certain physical questions not by directly solving the equations that we use in quantum field theory but by an indirect route, using fancy math. The answers one obtains in this way suggest that certain quantum field theories that we didn’t know about not only exist but have properties that are clearly inconsistent with the types of quantum field theory equations that we normally write down. (For example, we learned of quantum field theories whose symmetries could never arise from ordinary quantum field theory equations.) In particular, such theories cannot be even partially specified by what fields they have. This tells us that we’ve somehow been too narrow-minded, and there must be ways of defining quantum field theories using methods with which we’re currently unfamiliar.
What we know about this subject may be just the tip of a large proverbial iceberg. We know there are many of these theories, but we may not have identified the majority of them, or understood anything about what makes them special. Although the ones we know about are supersymmetric, there is absolutely no reason to think there aren’t non-supersymmetric ones too.
A Moral
From this story, I hope you can get some insight into why particle physicists spend a lot of time thinking about imaginary worlds. First, certain imaginary worlds might actually turn out to be real; second, what happens in an imaginary world may be analogous to, but easier to study than, what happens in the real world; and third, imaginary worlds may reveal phenomena that we never previously thought of and might be relevant for solving real-world puzzles.
The developments of the past 20 years have given us great insight into how quantum field theory works, thanks in large part to what we’ve been able to learn about supersymmetric theories, which are simpler to understand. It may turn out that supersymmetry has nothing to do with particle physics at the LHC, and the solution to the naturalness problem of the Standard Model. But for understanding how quantum field theory works overall, this is beside the point: supersymmetry as a tool for studying quantum field theory is here to stay. As a teacher of quantum field theory, I will say this: anyone wanting to understand quantum field theory fully must study supersymmetry. It’s not optional.



95 Responses
Greetings! Very useful advice inn this particular article!
It’s the little changes that make the most important
changes. Thanks a lot for sharing!
I don’t wish to put dampeners on this article, which is very informative and beautifully done, but to say that it created a seed of a doubt in me if supersymmetry is the right theory. On macro scale, we humans are greatly affected by a need for organization and apply strict rules to achieve good results. I see the same mindedness applied to a world of quantum particles, which doesn’t obey these rules. When I try to imagine what goes on inside a proton, I don’t think of pairs of particles perfectly balancing their act to obey some unwritten law of physics, though this must be so. I think of it as a compressed form of energy that can not be subdivided into smaller components. What we call particles are just various properties of that state of energy that when put together a lot is happening. there is a lot of attracting/repelling action going on in there. A bit like EM energy with its polarity, hadronic energy is a mix of a few interacting aspects of energy that result in a workable mechanism with a staggering consistency. I think of this mechanism as being less perfect than the quantum theory suggests. I see energy
not as one thing throughout the universe, dependent on matter, but a one flavor or combination of energy. the only combination that can create matter. Energy precedes matter, which is a confined state of energy submerged in a particular medium we call vacuum of space or quantum field.
If you had understood the article, Krystal, you would see it explicitly says that there is lots and lots of doubt among scientists as to whether supersymmetry is the “right theory” (or more accurately, *a property of* the right theory of nature.) That’s why one of the things we’re doing with the LHC is trying to look for signs of it… the way you resolve doubt in science is you do experiments.
The whole point of the article is that supersymmetry is useful even if it isn’t true in nature.
“Often, two quantum field theories with entirely different fields are actually the same” … this sounds a lot like isomorphism of vectorspaces, does the math to prove this look at least somewhat similar or im i way off? should i forget my vectorspaces math class to try to wrap my head around this one?
Frankly, I don’t understand this article. If the phlogiston (aether, epicycles, whatever..) model was disproved experimentally, then it cannot give us clues anywhere in real world, as this clue will be as misleading at the best case, as the concept itself. The note on alleged simplicity of supersymmetric quantum gravity theories doesn’t impress me very much, because as Einstein has said:”Things should be as simple as possible, but not simpler”. Well, what if the SUSY is just this “too much simple” case?
IMO this article just fulfills the Feynman’s remark: String theorists do not make predictions, they make excuses” in full extent. He said. “I don’t like that for anything that disagrees with an experiment, they cook up an explanation—a fix-up to say, ‘Well, it still might be true.'”
And this is exactly what I’m reading here.
+1000!
Ah, yes, birds of a feather — you’ve chosen an interesting person to agree with.
You’re not reading carefully, and I’ve seen several times that you have an axe to grind that prevents you from doing so. (A) I’m not a string theorist, I’m a field theorist, and I’ve never made any such excuses. (B) I’m not making excuses in this post. I’m stating facts. You don’t have to like the facts, that’s up to you, and you don’t have to like the approach, that’s also up to you. (C) your Feynman quote is completely off-the-mark in this article — I made the statement not that “Well, it still might be true” but rather “I’ve found it very useful for real-world problems even if it isn’t true.” It’s your loss if you’re unable to make the distinction.
Best of all, the SUSY as a concept wasn’t actually disproved with experiments. It just wasn’t understood. In AWT the well known SUSY particles are neutrinos – a superpartners of photons, which are all around us. The water surface analogy of SUSY is the duality of Falaco and Russel’s solitons. It means, the SUSY is thriving alive and well – just at different place, when everyone is expecting.
[You see what we’re dealing with here…]
BTW Wasn’t the SUSY predicting five Higgs bosons?
http://news.softpedia.com/news/There-May-Be-Five-Higgs-Bosons-or-None-at-All-331151.shtml
[Edited by host; link removed]
The smarter you try to make yourself appear, the more ignorant you reveal yourself to be.
Supersymmetry predicts 5 Higgs bosons, but does not predict that they will all be easy to find. The same is true of many other theories that predict more than one Higgs boson. This is unfortunate, but true; the other Higgs bosons make take several more years to uncover, and people are hard at work.
I strongly advise you to READ THIS: http://profmattstrassler.com/articles-and-posts/the-higgs-particle/taking-stock-of-the-higgs-jan-2013/4-more-than-one-higgs/
This is not a complete post I linked. I submitted the link to this picture, too. [Edited by host; link removed]
Please avoid the editing of my posts next time. The scientists should act honestly.
I do not advertise my personal ideas about physics on this website; this website’s purpose is to describe mainstream research to the public. This is not an advertising site. You have no automatic right to advertise your own personal ideas about physics on my website; that’s what your own site is for. I regularly remove people’s links to their personal pet ideas. If you don’t like it, go elsewhere.
I should, however, have marked your comment as “edited”; I was careless, apologies.
This doesn’t pass the smell test: “If the phlogiston (aether, epicycles, whatever..) model was disproved experimentally, then it cannot give us clues anywhere in real world, as this clue will be as misleading at the best case, as the concept itself. ”
Change for Newton gravity: ‘If the Newton gravity (aether, epicycles, whatever..) model was disproved experimentally, then it cannot give us clues anywhere in real world, as this clue will be as misleading at the best case, as the concept itself.”
Newton gravity is disproved (and general relativity is the more generic substitute), yet it is what rocket scientists use for directing crafts within the solar system.
Newton gravity wasn’t disproved experimentally – on the contrary: even the general relativity is using it in derivation of field equations. The Newtonian gravity is the local version of general relativity, but Einstein derivation of stress energy tensor is using the distance dependence of energy of gravitational field exactly by inverse square law. After all, this is just the way, in which gravitational constant G got into field equations.
It’s true there is a distinction. Newton’s gravity is incomplete and has to be extended, but it’s inside Einstein’s equations for gravity. But supersymmetry simply is not present in real-world particle physics, so far at least. And that is a logically different situation.
Indeed, your claim as stated is directly erroneous: “Phlogiston theory permitted chemists to bring clarification of apparently different phenomena into a coherent structure: combustion, metabolism, and configuration of rust. The recognition of the relation between combustion and metabolism was a forerunner of the recognition that the metabolism of living organisms and combustion can be understood in terms of fundamentally related chemical processes.” [ http://en.wikipedia.org/wiki/Phlogiston_theory ]
A few seconds contemplation gives me that empirical processes are recognized by that they learn from mistakes as much as from successes. Therefore there is no experimentally supported principle that states that experimentally disproved models aren’t informative on the real world.
Thanks for this comment, far wiser than my reply.
OK, if the SUSY will remain as useful and relevant for physics, as the phlogiston for chemistry, I think, I will have no problem with your stance.
You would be best off not to have a black-and-white, cut-and-dry view of intellectual history. Ideas that were once central disappear and are forgotten; others disappear for a generation and then return. And the positive impact of a wrong idea can be enormous; witness Sakurai’s 1960 theory of the strong nuclear force, which was as wrong as supersymmetry might turn out to be, but which nevertheless correctly predicted the rho mesons (which were discovered in 1961), and motivated Brout and Englert to do the work which won Englert the Nobel prize this year.
Bare particles are essential in all cases of QFT. As long as they are the true (but modest) bricks of everything, you are not dealing with physics, but with patched constructions far from true physics, in my opinion. http://vladimirkalitvianski.wordpress.com/2013/11/23/the-true-but-modest-heroes-of-microworld/
Is there any way of keeping the useful parts of supersymmetry while throwing out the parts that don’t fit with experiments?
It will be easier to sell others on the idea of supersymmetry if you can remove the prediction of particles that haven’t been found.
Are there symmetries that relate Fermions and Boson but that don’t predict new particles?
For example, it seems coincidentally that the current number of Fermions is 12 and the number of Bosons is 12 (or 14 if you count both the graviton & the Higgs Boson.) It also seems coincidental that the sum of the masses of all of the Fermions is on the order of the sum of the masses of the Bosons. (~180 GeV for Fermions and ~252 GeV for the Bosons, excluding the Higgs Boson…which is coincidentally half of the sum of the masses of the weak force carriers.)
These numbers don’t match exactly, but to summarize, it seems to me as though there might be symmetries between the Fermions and Bosons that don’t require the prediction of new particles. Could other symmetries help to simplify the calculations without requiring the prediction of “sparticles”?
Unfortunately, there seems to be no way. You can prove (http://en.wikipedia.org/wiki/Haag%E2%80%93Lopuszanski%E2%80%93Sohnius_theorem) that there are no symmetries between the known fermions and bosons that wouldn’t eliminate all particle scattering… That proof comes with some assumptions, but no one has found a way around it.
The one weird attempt I know of that had a shot of working also didn’t work, see the final segment of http://profmattstrassler.com/2013/08/21/search-day-1/ .
Matt,
Thanks for the follow up to the question. I read the wiki site, and I’m glad to see that people have already attempted the simple search for symmetries between fermions and bosons before landing on supersymmetry.
I was guessing that that a simple relationship between the number of known fermions and bosons was a stretch…because I wasn’t counting anti-particles and not counting color. I was just trying to seem if there was a way to save the useful parts of supersymmetry from the prediction of sparticles. One of the main drivers behind supersymmetry appears to be disappearing now that the evidence points to a dark matter particle of ~10keV rest mass.
(See Table II and Figure 2 of the following paper.)
http://arxiv.org/abs/1311.0282
Is there supersymmetry theory that is consistent with dark matter particles with a rest mass of ~2-20 keV? But with most other rest masses well above what we can measure?
S. Dino,
My counting was:
Bosons: 8 gluons, 3 Weakbosons, 1 photon
Fermions: 3 up-like quarks, 3 down-like quarks, 3 electron-like leptons, and 3 neutrinos
12 is an interesting number because it’s the number of permutations in S(4). If the number of bosons is really 13 or 14, then the chance that there’s an underlying symmetry is much less likely.
The particle counting above is ad hoc. It’s just that when I look at the particles in the Standard Model, I see a lot of order and structure that doesn’t seem to be predicted by the Standard Model, such as the -1, -2/3, -1/3, 0, 1/3, 2/3, 1 values for charge. The relationship between the Higgs Boson mass and the weakboson masses. The occurrence of precisely three families of quarks and leptons. The equal number of leptons and quarks, etc…
This is an exciting time to be studying particle physics. It is very likely that there is an underlying structure to what we are seeing. It’s just not the type of structure that has been guessed so far…such as GUT, supersymmetry, string theory, preons, etc…
I wouldn’t get too excited about 10 keV dark matter either; that’s just one paper and one line of argument. Four years ago lots of people were all excited about 10 GeV dark matter particles. These things often come and go as new information comes in and people explore new and old ideas. Only when we finally discover clear evidence will we know for sure. Dark matter could still be particles of 100 GeV, 1000 GeV, 1 GeV etc., … or not elementary particles at all.
It is very easy to make supersymmetric models with 10 keV particles, as long as those particles are not superpartners of any known particle. In other words, as long as the dark matter particle and its superpartner are BOTH unknown to us today, they can have almost any masses. That would mean they are not WIMPs (Massive Particles Interacting via the Weak nuclear force) but so what?
Hi Ed,
I hear you, and agree completely with your view that it is likely that there is an underlying structure to what we are seeing, but we just haven’t guessed at it yet. All the preon or subquark models that I am aware of have major problems to overcome. To me it seems like the elegant ones lack explanatory power – for example , Harari’s rishon model regards the muon and tau as merely excited states of the electron, and is helpless to explain why μ –>e + γ does not occur. Other models introduce additional preons that carry ‘generation number’ but these seem completely ad-hoc. And they all suffer the fact that there is not the slightest bit of experimental evidence for any of them.
What I would like to see is the discovery of a particle that is not predicted by the Standard Model but is predicted by one of these many theories (including, as I noted, my own).
Hi Ed,
Was just wondering: How do you get 12 (or 14) bosons? Are you counting each gluon separately, just based on color charge differences? If so, then shouldn’t you count each quark flavor three times also based on different color charges?
I actually have a theory (not yet published) that is naturally supersymmetric (but only in a certain sense). However, even this theory predicts extra particles one of which is an additional short-lived spin ½, charged lepton (beyond e, μ, and τ) with a rest energy of 360 to 370 GeV – which I assume would stick out like a sore thumb at the LHC…so it doesn’t look good.
A short-lived lepton in the 300-400 GeV range would not be produced with a high rate at the LHC, and I doubt it is ruled out yet. If, however, it gets its mass exclusively from the Higgs field, then it is indirectly constrained, but my recollection is that it isn’t quite excluded yet (it will affect the rate for Higgs to decay to two photons, which occurs via a quantum effect, see http://profmattstrassler.com/articles-and-posts/the-higgs-particle/the-standard-model-higgs/decays-of-the-standard-model-higgs/ )
Recent observations by gamma ray space telescopes has revealed gamma ray photons of 95 billion eV! My question is: is there any mechanism in QED that can generate a photon of such energies?
95 billion eV is not that big a deal: the photons in the decay of a Higgs boson are about 60 billion eV = 60 GeV.
As for QED processes, http://en.wikipedia.org/wiki/Fermi_acceleration . You can make photons far, far above these energies, by emitting them off the very highest energy cosmic rays. You can also make them when those cosmic rays collide with the cosmic microwave background photons; for a similar process that makes ultra-high energy neutrinos, see http://profmattstrassler.com/2013/05/16/possible-important-discovery-at-icecube/ . These photons are rare, though, so the chance of observing one on earth is very small. But they certainly must exist, because we observe both the cosmic rays and the microwave background photons.
Thanks for the references and also the enlightening reply.Much appreciated.
Thank you prof. Strassler for this synthetic and pedagogical defence of supersymmetry as a heuristic tool to improve : i) our understanding of the quantum field theories forged IN THE PAST and ii) build plethora of models for TOMORROW. But don’t you think that TODAY, at a time with only one Higgs boson and no superparticle detected by LHC so far (in agreement with null results of dark matter chasing experiments), it is time to focus instead on the possible conceptual reasons for the success of the only validated effective quantum field theory namely the Standard Model ? Now that (astro)physicists can reach so high energies and explore so huge amount of the unknown (but mostly empty!) universe don’t you think that priority should be put on mathematical and phenomenological consistency check of quantum theories ? Does supersymmetry ever help to deal with this topic ? My view is probably very naive but it seems to me that supersymmetry is not only a beautiful tool to enlarge the plato cave that fits with our prejudices (built on former empirical and mathematical experiences) but to say it crudely, it is also the most powerful tool physicists invented to sweep the dust under the carpet!
“it is time to focus instead on the possible conceptual reasons for the success of the only validated effective quantum field theory namely the Standard Model”
Yes, I agree with this statement, personally. This is what I’m doing. But it’s not easy… people have considered this for over 30 years and I don’t think there is a convincing story.
However, as I emphasized, studying supersymmetry has been extremely helpful in learning to understand quantum field theory in general. Several of my best ideas for dealing with non-supersymmetric field theories came from studying supersymmetric ones. I have just been reading up on the most powerful new tools for studying non-supersymmetric theories in two spatial dimensions, many of which relied upon results and/or insights that emerged in supersymmetric contexts. So I think your statement “it is also the most powerful tool physicists invented to sweep the dust under the carpet!” really is too crude, not only in its tone but in its content. It’s much more elaborate and subtle than that.
Thank you for the fast feedback. I don’t aim at being rude to SUSY, as you understand perfectly, the more so as it could show up “in our face” at any time from future experiments or from data currently processed by tenacious physicists.
On the theoretical side, nevertheless I have the feeling that supersymmetry has been oversold by the media and science outreach in general. I can understand that other mathematical tools, inspired by quantum physics, like quantum groups, Hopf algebra and non commutative geometry for instance are very hard to popularize but they seem to be less studied by theoretical physicists as well while they have proved to be useful : i) to envision a mathematically coherent picture of renormalization, ii) to calculate the quantum numbers of the discovered Higgs boson and iii) to build possibly phenomenologicaly coherent SO(10) grand unified theory-like models (sorry for loosing non experts, I don’t intend to be pedantic, just specific).
Of course this is just a feeling from a “periphysicist” so to speak. I am not involved in research, just a curious educated hiker on the cybersphere looking for a piece of physics information to better enjoy the beauties of the world.
Once again Bravo ! for your work in this blog 😉
It is a fair point that supersymmetry has been somewhat over-studied (just because people like to play with it) compared to other promising ideas. This is partly because so much progress was made using it in the 1990s — that drew people in, of course. When there’s a breakthrough, people tend to go where the action is, but then they tend to stay longer than perhaps they should. It would definitely be good for people to spread out more.
Excellent article and a nice addition to this truly great series. However, I believe there is one minor mistake. Shouldn’t Figure 3 be 8 x *5* quark and squark fields and *24* gluon and guino fields, i.e. SU(5), not SU(4)? Perhaps I am missing something?
I apologize if this sounds nitpicky–I think this is an excellent series about QFT and I simply thought you would want to know if there was a mistake.
Thanks! — obviously I was working after midnight, and forgot midstream what I was trying to do. See if the current version is now correct (SU(3) with *7* flavors dual to SU(4) with 7 flavors + singlets.) — no more mistakes I hope!
Yes, I completely understand your mistake! It was a very simple mistake to make when creating such nice diagrams 🙂
Honestly, it’s your papers on this subject in particular that drove me to the site. As a graduate student learning the subject, I find them similar to the your pedagogical and intuitive explanations on this site, except for advanced audiences. I am particularly fond of hep-th/9708091 and hep-th/0309140 as they highlight some of the importance of this area of work in a broader context. This is really useful since it is no longer the mid-90s and I don’t get to hear experts come and speak on these ideas (I feel this kind of broader implications is often emphasized a lot more in talks then in journal articles). Anyway, I guess what I am saying is thanks!
Nice post. But can you stop using the initial label laying out the appropriate readership? It is quite condescending.
Well, OK, thanks for the feedback. I’m trying to figure out the best way to help readers figure out which posts are for them. Do you have an alternative suggestion? The problem is that many readers find themselves facing an advanced post, and leave the site unaware that there are also many posts and articles that are suitable for a person with no background in particle physics.
I disagree with Ray. I find the labels helpful. Even though I consider myself an advanced non-expert, I still like to know before hand the level of what I am about to read. If it is marked “advanced” I may put it off until I am less likely to be interrupted.
I can also imagine that some readers with less background knowledge who like the site in general would want to stay away from the advanced articles.
I would say that if your goal is to make people aware that there are articles suitable for people with no background in particle physics, then the “Appropriate for Advanced Non-Experts” label doesn’t quite do it. That label implies there may be other types of articles, but does not provide information on how one would find them. Putting the label next to a link to an “article difficulty ratings explained” page would be helpful for someone who stumbled upon a difficult article and was looking for a more appropriate one on the site.
Excellent post. I have read many articles and books for the advanced non-expert, but have never seen the usefulness of supersymmetry explained in this way.
By the way, there is a typo in the next-to-last sentence before Figure 1.
You write “that’s a much more complex issue that I want to cover here”, but mean “that’s a much more complex issue than I want to cover here”. Just one letter difference, but opposite meanings.
Thanks!
Matt said,
Frenkel is not a particle physicist and has not worked directly on this subject, so I’m curious to see how much he really understands of what we’ve learned in this field.
Matt, I did not mean to make it sound like Ed Frenkel was representing in his book that he was an expert in the field or particle physics, but simply that he was able to show how the use of mathematics and duality can help particle phycists do their jobs. He does clearly advocate for mathematicians and physicists to work together to the mutual benefit of both disciplines. From my perspective he does seem to have a fundamental understanding of this subject.
And apologies, I didn’t mean to sound snide about it — I am just curious to see what he really knows.
Is SUSY splitting the magnetic field into two symmetric magnetic particles ( North and South)?
No, there’s no connection between these things. North and south magnetic poles are related by other, simpler things, such as reversing the direction of all electric currents.
This sounds like magnetic monopoles … ???
Complex variable math is a little more subtle than that. In fact, Complex numbers allow to use an elegant and simple set of concepts and equations to represent problems of the real world.
For instance, De Moivre’s formula offers a simple and alternative way to represent waves with cartesian pairs of numbers.
It is much simpler to solve complex sets of PDEs with transforms like Laplace or Z, and we need to use complex variable for that.
In fields like electrical engineering, or instrumentation and control systems engineering, the use of complex variable formulas is common place, and both domains deal with real-world stuff.
Kind regards, GEN
For supersymmetry, the truth lies somewhere between; it is not quite as ubiquitously useful as imaginary numbers are. Still, there are times where making a problem look supersymmetric at an intermediate stage makes it easier to solve the problem, much as making a problem of real numbers into a problem of complex numbers can make it easier to solve. Mostly, however, it has been useful more by what it teaches by analogy than by direct application. Maybe that won’t always remain the case.
A great introduction to the essence of super symmetry to any one interested in HEP.
It appears to us who are standing outside and peering into the world of super symmetry through your articles, that it is very similar to the development of imaginary number apropos to the real number. The square root of minus one does not exist in the real world but provides a powerful mathematcal tool to tackle the real world problem.
Thanks again for your wonderful article and the effort that was taken to make it clear for us lay folks.
Complex numbers do exist in the real world. They are simply obtained by imposing the following rules for multiplication and addition on R2.
(a,b)x(c,d)=(ac-bd,ad+bc)
(a,b)+(c,d)=(a+c,b+d)
and then call i=(0,1) and you will see ixi=(-1,0) which is then abbreviated as i^2=-1.
Sorry Matt. , but I am confused :
Is the situation now : we cannot solve for real Hadrons unless we introduce. SUSY , or even with Susy we cannot solve for the real Hadrons?
Execuse my stupidity!
Sorry for the confusion.
Some things about hadrons we can learn directly from computer simulation: http://profmattstrassler.com/2013/10/07/quantum-field-theory-string-theory-and-predictions-part-4/ .
But other things about hadrons we don’t know or understand very well, either because computer simulations of those things aren’t possible, or because the results of the computer simulations are not very explanatory.
Some supersymmetric theories also have hadron-like objects, and we can study those using fancy mathematics.
This gives us a second route to learn things about real-world hadrons, by analogy; it’s not as direct as computer simulation, but it provides insight into issues where computer simulation isn’t useful or possible.
In point 2), you mentioned the following: “The only way to figure out the right theory is to guess it starting from data.”
Do you mean Ansatz is used to find a more general solution (validated afterwards by comparing the predictions with data) by starting from a set of assumptions (educated guesses)?
Kind regards, GEN
It is indeed a method of an Ansatz which you check against data. But the Ansatz that is used emerged gradually as people understood various aspects of the data — for example, by comparing processes that seemed to have the same probabilities of occuring, they noticed interesting relationships among different physical processes that were then incorporated into the Ansatz.
I do not understand why one would add up a,b,c, since presumably b (with symmetry breaking!) may contain a and c. Is this right?
Sorry. I meant: I do not understand why one would add up a,b,c, since presumably a (with symmetry breaking!) may contain b and c. Is this right?
It’s just a clever trick to get an answer to an otherwise complex question. The trick is to recognize that a is a simple formula, b is a more complex formula, c is the most complex, and that the final answer is the sum of the three. You don’t want to go around breaking any symmetries, because by breaking the symmetry you’ll make “a” and “b” a lot more complicated. You want to keep all the symmetries, because that’s what makes “a” simple and what keeps “b” only moderately complicated.
Great article!
In point 1) from the section “Learning Lessons From Supersymmetry”, you mention that steps a) through d) are used to do a successive approximation calculation for the Standard Model.
Step d) clearly states “add them up, with appropriate care”. I have some simple questions regarding this method:
It looks very much like when you solve a system of partial differential equations (which the might actually be!), and you can get a general solution by applying a linear combination to a set of particular solutions to the system of equations:
is that right? is this what is being done?
When you say “with appropriate care”, are you talking about renormalization?
after all, you are using some sort of pertubation theory here, so, it is likely that infinite integrals may pop up, and you have also mentioned “low-energy, large distance”, so, there might be a need to handle the relationships, specially the differences between the parameters for short distance scales and the parameters for the long distance scales.
Kind regards, GEN
Renormalization, and proper removal of the fake infinities, is only a small part of this story. I don’t think I have time to describe it right now. It’s more like figuring out how to write
Answer you want = A + B + C
where A is simple, B is more complicated, C is very complicated. By breaking the calculation up this way, you focus your attention on C, because A and B are now pretty easy (and these come from supersymmetric theories). C is intrinsically hard, and you have to work at it, but you can calculate it in a relatively simple non-supersymmetric theory.
So the “appropriate care” is really about figuring how to break the calculation up in the first place into A, B and C.
Ha-ha! Fake infinities! Fake results, you mean. If the theory gives “a” and you need “b” (you know it in advance), do the following: write a=b+(a-b) and then subtract the bracket. This is your “appropriately taking care”.
I’m sorry, but the joke is on you.
https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PAPERS/STDM-2011-06/figaux_23.png
I could send you 10 other plots. It works just the way I say it does, and all of your complaints are in contradiction with data.
It was not a joke, it is what you do with loop corrections. And do not tell me about “bare parameters” who “absorb” infinities. It is we who subtracts them. You just do not consider it a fake, but it is.
This is irrelevant; the discussion of today’s post has essentially nothing to do with the infinities anyway. It has to do with various types of (finite) functions of increasing complexity that do or don’t appear in calculations within theories with less or more supersymmetry.
But there are no exp. yet w.r.t.SUSY
1) There are many experiments that have looked for signs of supersymmetry in nature; that’s how we know that supersymmetry does not describe the phenomena we have so-far observed.
2) We know from theory that minimal supersymmetry might show up in future experiments, so whether supersymmetry might be relevant to the real world remains an open question.
3) We know from theoretical study that some supersymmetric theories exhibit phenomena which are similar to ones that show up in non-supersymmetric theories that do describe the real world; one example of such a phenomenon is hadrons, http://profmattstrassler.com/articles-and-posts/largehadroncolliderfaq/whats-a-hadron-as-in-large-hadron-collider/ . We can use supersymmetry to study these imaginary hadrons and why they are present, in hopes of learning lessons that are relevant for the hadrons of the real world. So: no experiments on supersymmetry here, but theoretical calculation are being used to obtain insights that potentially relevant for the real world. Not directly relevant, mind you! No predictions are made for a real experiment about known real hadrons; they’re just made for the imaginary ones. But still, possibly a conceptual stepping stone toward understanding. And (see (1) above) just possibly relevant for future experiments.
1) There are many experiments that have looked for signs of supersymmetry in nature; that’s how we know that supersymmetry does not describe the phenomena we have so-far observed.
2) We know from theory that minimal supersymmetry might show up in future experiments, so whether supersymmetry might be relevant to the real world remains an open question.
3) We know from theoretical study that some supersymmetric theories exhibit phenomena which are similar to ones that show up in non-supersymmetric theories that do describe the real world; one example of such a phenomenon is hadrons, http://profmattstrassler.com/articles-and-posts/largehadroncolliderfaq/whats-a-hadron-as-in-large-hadron-collider/ . We can use supersymmetry to study these imaginary hadrons and why they are present, in hopes of learning lessons that are relevant for the hadrons of the real world. So: no experiments on supersymmetry here, but theoretical calculation are being used to obtain insights that potentially relevant for the real world. Not directly relevant, mind you! No predictions are made for a real experiment about known real hadrons; they’re just made for the imaginary ones. But still, possibly a conceptual stepping stone toward understanding. And (see (1) above) just possibly relevant for future experiments.
Another excellent post, Matt.
As a grad student in physical chemistry who loves studying physics on the side, it seems to me that QFT has a fundamentally different mathematical structure then just about any other physical theory I’ve seen. All other physical theories can be understood using PDEs and linear operators/algebra (with GR requiring algebraic geometry beyond that). From my perspective, QFT stands out from the rest. Is this reasonable intuition? Do you thing about this the same way or know a reason why this might be?
The only place I’ve seen anything resembling QFT is in statistical theories that can be renormalized, such as the spin Ising model. But these theories seem to only be similar on the surface and don’t seem to have the deeper surprises of QFT, such as the ones you mention in this post.
A simplistic non-expert take on that: When you treat a physical system with N (classical) coordinates in (non-relativistic) quantum mechanics, the behavior is governed by the Schrödinger equation which is a PDE for the wave function in N+1 variables.
By analogy, when you treat a field theory with its infinite number of degrees of freedom you would get a “PDE in an infinite number of variables” for the “wave functional”. While this is of course not a mathematically correct or technically useful way to put it, it may give an idea of the complexity involved in QFT – considering how hard it is already to solve PDEs in just a handful of variables.
The problem I have with this reasoning is that it doesn’t explain why classical field theory and GR can be described by finite numbers of PDEs even though they have infinite degrees of freedom, yet there does not seem to be any such formulation of QFT that I am aware of.
Classical particle: 3 degrees of freedom, whose motion is described by a 3 differential equations in time
Quantum particle: 3 degrees of freedom characterized by a wave function (a function of 3 degrees of freedom) described by a partial differential equation in three dimensions of space and in time.
N classical particles: 3N degrees of freedom, whose motion is described by 3N differential equations in time
Quantum particle: 3N degrees of freedom characterized by a wave function (a function of 3N degrees of freedom) described by a partial differential equation in 3N dimensions of space and in time.
Classical field in d spatial dimensions: infinite degrees of freedom arranged in d-dimensional space, whose motion is described by a differential equation in d-dimensional space and time
Quantum field in d spatial dimensions: infinite degrees of freedom arranged in d-dimensional space, characterized by a wave function (a function of an infinite number of degrees of freedom) described by a partial differential equation in an infinite number of dimensions and in time.
You see the quantum field situation is by far the worst. It’s so bad that we don’t use wave-functions to do calculations. We use other methods that can better handle the infinite numbers of degrees of freedom and make use of the fact that those degrees of freedom are arranged in d-dimensional space.
When you get to quantum gravity, even the space and time start moving on you.
“Classical particle: 3 degrees of freedom, whose motion is described by a 3 differential equations in time…”
Equivalently we can use a _field_ description with S(x,t) in the Hamilton-Jacoby equation.
The QFT problems are rooted in the self-action idea, not in the infinite-dimension description. We handle SM difficulties with removing self-action contributions, which are simple by chance in this theory.
In GR and other non-renormalizable QFT the self-action spoils equations so badly that simple subtractions are not sufficient and nobody has an idea what else should be modified (removed and added) to get a reasonable result. That’s my impression.
It is true, and a good point, that you can use the Hamilton-Jacobi formalism instead of Newton’s, and this will make classical mechanics look a lot more like the quantum case. Indeed, no one ever writes Hamilton-Jacobi equations for classical fields, because they are functions of an infinite number of degrees of freedom, and quite challenging to use.
Very importantly, I do not think you should call the Hamilton-Jacobi function S(x,t) a field. A field is always a function of 3 dimensions (more precisely, of d dimensions, if you live in d-dimensional space.) But if you are describing two particles movinh in 3 dimensional space, the Hamilton-Jacobi function S(x1,x2,t) is a function of six spatial variables, showing it is more like a wave function, not like a field. One of the biggest and most common mistakes students make in my field theory classes is confusing wave functions and fields; fields are always functions of 3 spatial dimensions, while wave functions are functions of all the configurations of the system they describe, and are functions of potentially huge numbers of dimensions (except when they describe one and only one particle.)
Regarding the self-action vs. infinite-dimensional description; I am not sure you understood the question that the commenter was asking. This is not a relevant point; even in maximally supersymmetric field theories, where all self-action contributions cancel and no removal is necessary, you still have infinite numbers of degrees of freedom described by a wave function that satisfies an infinite-dimensional partial differential equation.
“you still have infinite numbers of degrees of freedom”
As far as we (you) handle them, it is not a problem, so let us not hide re
So, I may be biased given that this is the current focus of my research, but I think it’s an overstatement to dismiss all supersymmetric lattice gauge theory calculations as “a complete disaster”. They are certainly trickier than lattice QCD (or straightforward generalizations thereof), and it has taken a long time for the necessary clever ideas to accumulate, but for several years now at least some special cases (such as N=1 SYM and N=4 SYM) have been tractable. I don’t believe the situation is nearly as dire as (for example) that of chiral lattice gauge theories we discussed in the comments on the previous post in this series.
Hi David,
This is a question I have been wanting to know more about, but don’t have much of an idea where in the lattice literature to look for introductory references. I’m a graduate student working on some aspects of confinement in supersymmetric theories. I have wondered what the lattice has been able to say; in particular, I am curious about what happens if you softly break SYM with a gaugino mass term and then increase that mass term. Do the number of vacuum states change? If so, what kind of phase transitions do you see? etc.
Do you have any references that might point me to clues from the lattice community about these questions? Also, are there any good, pedagogical reviews that give a picture about what the lattice has learned in relationship to SYM and YM? I don’t intend to do lattice calculations, but I would like an understanding about what insights it has made.
Also, do you know if there is a way to simulate magnetic monopoles on a lattice or what progress has been made towards this end. In particular, the basis of lattice calculations is around a Wilson loop. I am curious as to the study of ‘t Hooft loops (magnetic source charges) and how they might be implemented on a lattice.
Thanks,
Brian
p.s. I believe you were a graduate student when I was an undergrad at BU. Go terriers!
Excellent questions — but perhaps best discussed in a different venue than the comments on Matt’s blog. I’ll follow up directly.
Matt. Nice article.I am interested in understanding little better your remark:”Supersymmetry is a complete disaster for computer simulations; the methods we have for simulating quantum field theories using computers do not work at all in the presence of supersymmetry.” Is this because SUSY does something to space-time grid which you need for computer simulations?
Sort of the reverse: the space-time grid ruins supersymmetry completely, so all the nice features of supersymmetry are lost and you would have to struggle greatly to get them back.
On top of this, supersymmetry with any interesting sorts of forces requires massless spin-1/2 particles (superpartners of the force particles), and massless spin-1/2 particles are extremely difficult and time-consuming to try to simulate.
Nice article Professor, thank you. Massless spin 1/2 particle is an imaginary ?
We don’t have any known spin-1/2 massless particles in nature right now. They certainly are allowed to exist in our universe, we just don’t happen to know of any.
Amazing, so gauge bosons (virtual particles or evolutionary idea) is a certainty – replacing uncertain perturbation theory with supersymmetry.
A conservation law states that some quantity X in the mathematical description of a system’s evolution remains constant throughout its motion — it is an invariant. Mathematically, the rate of change of X (its derivative with respect to time) vanishes, dX/dt = 0. Such quantities are said to be conserved.
Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called gauge invariance). When such a theory is quantized, the quanta of the gauge fields are called gauge bosons.
The redundant degrees of freedom is ensured in supersymmetry as a physical reality ?
Spin 1/2 massless particles and massive spin 0 particles cannot coexist in same energy.
Isomorphism may relate them – in context with space-time grid. ?
I have poor knowledge about special unitary group (SU(n)) mathematics.
Sorry, if any fundamental thinking mistakes !
With respect to duality, Edward Frenkel, in his new book, Love and Math: The Search for Hidden Reality, has an excellent explanation of duality and its application to particle physics.
Frenkel is not a particle physicist and has not worked directly on this subject, so I’m curious to see how much he really understands of what we’ve learned in this field.
Take a look at Frenkel’s book (esp., Chapters 16 & 17, and the endnotes to those chapters). It’s funny how similar what you are saying about supersymmetry in this post is to what Frenkel is saying about it in his book. Not entirely surprising, given that Frenkel has collaborated with physicists such as Ed Witten.
will do.
In all this huge web of equations , what is the measure that define to us that we are dealing with reality not imaginary reality ?
experiment.
Excellent writing and analyses. I will read your work more deeply