What is supersymmetry?
Supersymmetry is a conjectured symmetry of space and time — and a unique one. It has been a very popular idea among theoretical physicists, for a number of reasons, for several decades — it was a hit back when I was a student, before physics was cool, and even well before.
An automatic consequence of having this symmetry in nature is that every type of particle has one or more superpartners — other types of particles that share many of the same properties, but differ in a crucial way. If a particle is a fermion, its super-partner is a boson. If a particle is a boson, its super-partner is a fermion.
What are fermions and bosons? Click here to find out!
Our world has many fermions — all the matter particles — and many bosons — all the force carriers. But none of them have the right properties to be super-partners of one other. So therefore, if supersymmetry were a symmetry of nature, every type of elementary particle that we know of in nature would have to have partners we have not discovered yet. Since there are over two dozen particles known, that would mean we have a lot of work left to do!
What is this symmetry, really? [You can safely skip this part if it makes you queasy.] It is a symmetry that relates space and time themselves to superpartner directions of space and time — in other words, space-time itself has extra dimensions quite unlike the ones we know. In a bosonic dimension — the ones we are used to — you can move as far as you want, taking step after step to the left, say. Moving in a fermionic dimension, it is as though you can only take one step. Take a second step in the same direction, and you’re nowhere. The only thing you can do is go back. Ok, that sounds really weird, and it is; in the end, you have to define that kind of dimension using math, not words or analogies.
Einstein’s theory of relativity does a beautiful job of describing and predicting many aspects of our world. His theory consists of a set of equations that obey a certain set of symmetries. (An example is translation symmetry, or symmetry under moving the experiment from one place to another in time or space: the same experiment done today in London will give the same result when done a few months from now in Tokyo.) It was proven mathematically in the 1960s that supersymmetry is the only symmetry that can be added to the symmetries of Einstein’s theory without making the resulting equations inconsistent with the world we live in. So supersymmetry is, in this sense, very special.
Where are those superpartner particles?
Were supersymmetry an exact symmetry of nature, we would already have found many superpartners.
Before going further, you might want to remind yourself about the known elementary particles, which are reviewed in this article [if you click on the link it will open in a new tab, so you can have it handy for reference] Figures 1 and 2 of that article are particular useful to glance over and compare with the figures that are coming below.
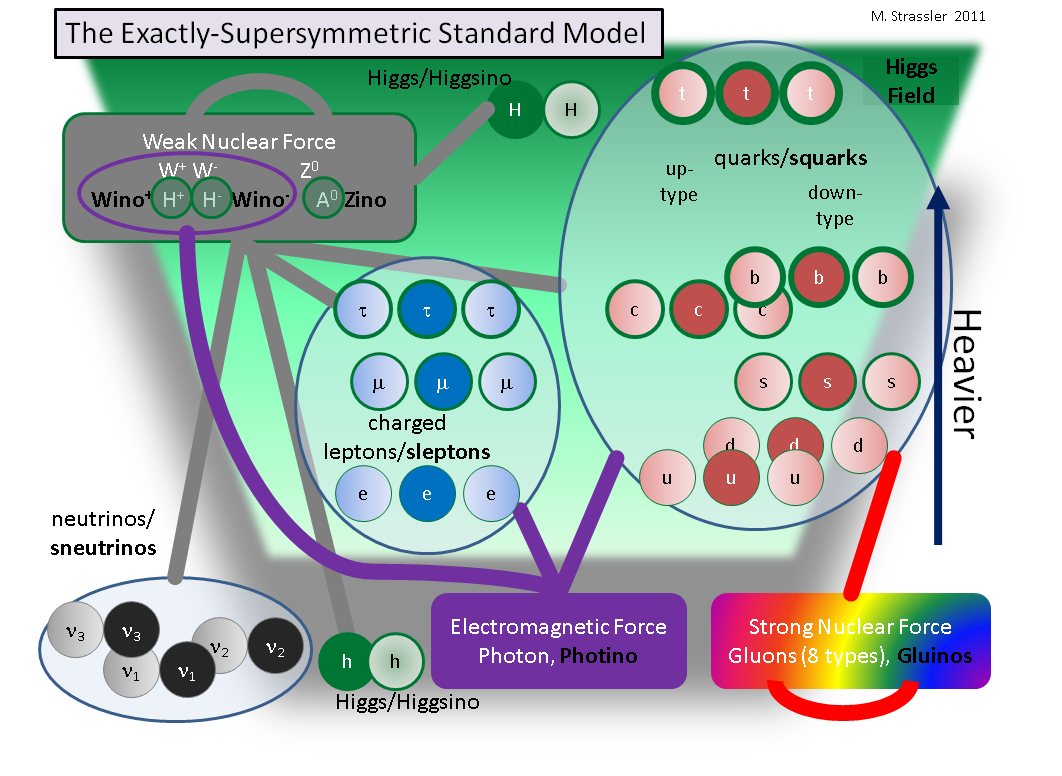
In Fig. 1, I have shown what the particles of the world would be if the Standard Model was combined with exact supersymmetry.
- For each matter fermion, such as the electron or the strange quark, you see that there are two new particles… both bosons. (They have rather ugly names, I am afraid, such as selectron and strange squark, the s prefix standing for supersymmetry.) You might wonder why there are two (and why there is only one for each neutrino.) Take a look at Fig. 3 of this article, and with a little thought, you’ll see why.
- For the force carrier bosons, they instead have a partner fermion. The photon has a photino, the gluons have gluinos, etc. The massive W bosons are a little more confusing. They have a partner wino (ugh, these names) and also a partner Higgs, called the H+. (Caution! This particle is NOT to be confused — despite it having the same name, which is often a problem in particle physics — so many particles, so few letters — with the H+ that appears in many Figures of this article on what would happen in the [ordinary not supersymmetric] Standard Model if the Higgs field were zero.) All of these particles have exactly the same mass, in this imaginary exactly-supersymmetric world.
- There are two Higgs particles h0 and H0 in this model, and each has a partner Higgsino. One is massless and the other has a mass. Why two? Turns out that in a supersymmetric world you need two to allow both the up-type quarks and the down-type quarks to get their masses in the usual way. Another argument is that you need two higgsinos to avoid mathematical inconsistency.
But this exactly supersymmetric world is obviously not our world. As indicated in the figure, in such a world particles and their superpartners
- share exactly the same interactions with other particles and their superpartners
- have exactly the same mass
Now we would have known a century ago, or more, if there were particles in the world that had the same electric charge as the electron, and had the same mass as the electron, but weren’t electrons. For one thing, we would have atoms with electrons in them, and atoms with selectrons in them, and atoms with both. The number of types of atoms would be much larger than we observe, and because bosons in atoms would behave utterly differently from fermions in atoms, the chemistry of the new atoms would be unrecognizable. Data and daily life completely exclude this possibility. There are no selectrons with the mass of the electron, period. So exact supersymmetry is not a correct theory of nature, and we knew that before supersymmetry was first thought of.
End of supersymmetry…? Not so fast.
Despite this seeming disaster, the original theoretical proposal of supersymmetry allows a very simple and even plausible way out. It is a common notion in physics that symmetries may be hidden from view (physicists often say spontaneously broken, but really this is not a good image to have intuitively — the symmetry is still there, it has just been made difficult to recognize.)

One example involves rotational symmetry on the earth. The laws of nature are the same no matter how you rotate your experiment (see Fig. 2). This is true, but hard to recognize on earth, where it does matter whether your experiment is right-side-up, up-side-down, or tilted sideways. But far out in space, far away from all the planets, moons and stars, the laws of nature are rotationally symmetric. Your experiment will give the same answer no matter how you orient it. (Incidentally, measurements of light emitted from very distant atoms do indeed confirm this.) What the earth does is confuse us. It makes us think that down is a very different direction from up or from left. But that apparent difference is not intrinsic to the laws of nature. The difference arises because the earth is nearby, hiding rotational symmetry from our view.
The question is, then, what if some aspect of our world [not something crude like the earth, but something subtle similar to a Higgs field, suffusing the universe and changing its properties] hides supersymmetry from view, everywhere throughout the universe? What would happen then? It turns out that it is quite easy to get a world that looks just like ours, in which the superpartners of the known particles exist but have become heavy… too heavy for us yet to have produced them in experiments.
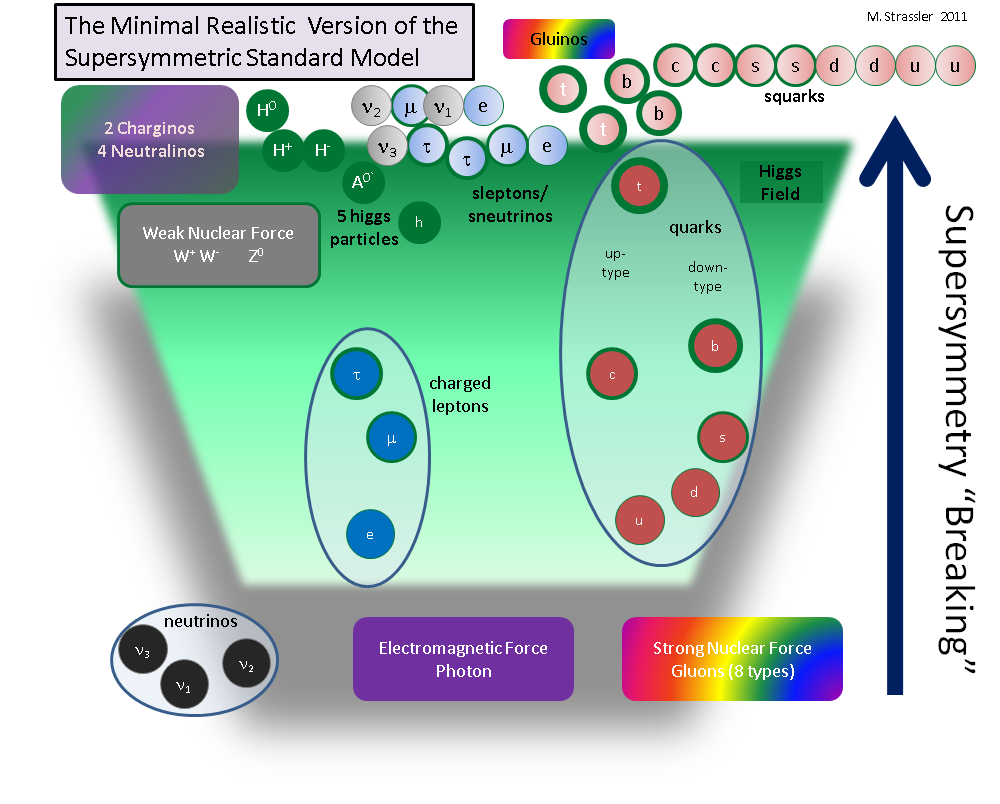
A realistic possible world of this type — and perhaps it is similar to our own — is illustrated in Fig. 3. You see that supersymmetry breaking (the hiding of the symmetry from easy view), whose details are not specified, has pushed all the superpartners up to a mass scale around or above the top quark mass. This is not as arbitrary or silly as it sounds — the mathematics readily accomodates this effect. There are many precise examples of how this could happen… but far too many for us to guess which of them is most likely.
In this possible world I’ve illustrated for you, I’ve made some arbitrary choices, but ones that are quite common in detailed examples of supersymmetry breaking that have been studied by theorists like myself:
- the squarks and gluinos have all gotten large masses
- the sleptons and sneutrinos have all gotten large masses, but perhaps slightly smaller than those of the squarks and gluinos
- the winos, zino, photino and higgsinos have all gotten mixed together into a set of electrically charged particles called charginos and electrically neutral particles called neutralinos, some of them possibly only a bit heavier than the W and Z particles.
- the five higgs particles now have a wide variety of masses, though at least one of them is quite lightweight
This is by no means the unique pattern that could occur through supersymmetry breaking! There are many, many other possibilities, which I will refer to as different variants of supersymmetry. But the kind of pattern I have drawn here is by far the most popular among theoretical physicists and experimental physicists, especially in Europe, somewhat less in the United States (and I’m not sure about elsewhere). There are some good reasons for this popularity; it turns out there are a number of independent ways to get a pattern similar to this. However, popularity always introduces bias, and we should keep our minds open, not simply assuming these good reasons are correct.
But if the superpartners are made heavy, isn’t it likely that they are so heavy that we won’t be able to make any of them for decades or even centuries? in which case, aren’t we on the verge of counting angels on the head of a pin? From what I have told you so far, yes, that would most definitely be a risk. However, there’s another more subtle argument in favor of supersymmetry that makes many physicists hopeful that all of those extra superpartners might lie within reach of the Large Hadron Collider. This arises from the fact that supersymmetry would solve the hierarchy problem, one of the great puzzles about our world.
What is the hierarchy problem? How does supersymmetry solve it? And what does the Large Hadron Collider data have to say, so far, about supersymmetry? Stay tuned.


28 Responses
Are they all heavier by the same amount or is it more complicated
What is the particular relation between the partner masses and vacuum energies
Hi, Joe Layman here. It seems like the end result of supersymmetry is that half of this universe is superluminal and we don’t have the ability to conceptualize it, which is why we have zeros and infinities in our math. Perhaps we need to consider an algebraic math as fundamental, and digital math is the real entropy; thus explaining the need for zeros and infinities in our work.
Well Bernie, that was a bit harsh..
Fuck you!
Hello, I doubt this thread is still active, but come across it and am curious as to a section. It states that we would have known if there was a particle with the same mass as an electron ages ago, but we do. In 1929 the Positron was theorized and later proven to exist. Is this not what was being alluded to? How does this change the state of the argument?
Thanks.
No. First of all, a positron has the *opposite* charge of an electron, not the *same* charge like a selectron. Second, a positron is a fermion, whereas a selectron is a boson (that’s the whole idea of supersymmetry).
The positron is just the antiparticle of the electron. That means it’s mathematically kind of like having “one less electron than none at all”. That doesn’t have anything to do with supersymmetry.
I will comment that i like reading books.
I think the admin of this website is actually working hard in support of his web site,
because here every data is quality based stuff.
Dear Dr.Strassler,
I have a problem about h0 and H0.
In our world so far we know, when a right-chirality fermion (excluding neutrinos) meat a Higgs boson, then the right-chirality fermion would turn into left-chirality fermion. This mechanism only need one Higgs boson for all fermion, except neutrino, including up-type quarks u c t and down-type quarks d s b, if my concepts were right.
Why in the SUSY world, however, need two Higgs h0 and H0? You said, under Fig.3, that we need 2 Higgs to allow both the up-type quarks and down-type quarks to get their masses. Why in the original world, we just need one Higgs to allow the up-type quarks and down-type quarks to get their masses, but in SUSY world we however need two Higgs to allow the up-type quarks and down-type quarks to get their masses?
Hi,
What about anti-matter? i.e., why couldn’t the electron’s superpartner be the positron?
imdavidfindley@gmail.com
veyr eager to know, thanks!
sleptons/sqarks have s=0 sorry for the typo.
Hi Prof.
In Fig1. and on the page about the Higgs mechanism/SM you assume the Standard model + Higgs field, has 4 Higgs particles (H0,A0,H+,H-). I guess you assumed therefore that the Higgs sector is extended, and that there are 2 Higgs fields with (2 complex SU(2) douplets). What is the main motivation to assume this extension? And is it this extension of the Higgs sector that can give rise to CP breaking in the SM?
In Fig 1. you have drawn the photino and gluinos as forces (spin 1 bosons). But since they are the photon and gluon superpartner, wouldn’t they be spin 1/2 fermions? And do you know if there is any significant effect of the superpartners of leptons and quarks (s=1/2), the sleptons and squarks (s=1) have, being a scalar, on the energy density of the vacuum? (I suppose since the Higgs vev is already in violation with the observed vev, the sfermions make things even worse).
Many thanks.
楽天golf dior 表参道 http://biantaicp.celinebyimmediatelyjp.org/
バッグ レザー はんこ 手作り http://wanchuanjc.leeahuepajp.org/
You touch briefly on the nature of the symmetry itself and claim that it has to be defined “using math, not words or analogies”… but I wonder: is there really no other way to explain what its true content is (except for the existence of new particles)? Would be greatly appreciated!
I’m sorry, but the math behind supersymmetry is both very complicated and very surprising. I would never have guessed how it works, had I been told such a symmetry existed and not been shown the mathematics behind it. I can tell you that it is a way of adding fermionic dimensions to the bosonic ones we are used to, and that there’s torsion which is crucial to make it all work out, but what good is that going to do you?
On the question of why there are two superpartners to each fermion, except the neutrinos: I can make the obvious guess that this has its origins in the left- and right- versions of particles as described in your article on “what if the Higgs field were zero”. But it’s not quite clear to me why the Higgs mechanism, as described in that article, only unites the left- and right- versions of the “ordinary” particles (e.g. the top-left and top-right particles get united into the top quark) but doesn’t do the same for the left- and right- superpartners (so we might end up with two superpartners to the top quark, of different masses). Is it just because the superpartners are bosons, and the Higgs mechanism deals with bosons differently? In which case, is there anything simple that can be said about how those superpartners get to have non-zero mass, or is it another complicated story that would need an article to itself?
Also, your Fig. 3 here suggests that the superpartners to the 4 lightest quarks all have the same mass, whereas those of the b and t quarks, and of the charged leptons, have different masses. Is that what (a version of) the theory predicts, or just an artefact of the diagram?
In fig 2, are you sure that the scalar partner to the Z0 is A0 and not h0? I guess that the CP-odd neutral higgs seems more adequate for the massive Z supermultiplet, but looking at the tree level masses of the MSSM, the only way I see to restore mass equality of W+ and H+ is to set the mass of A0 to zero, and then the masses of h0 and H0 go one to zero too, other to mZ. So it seems as if the higgsino partners were a CP odd and a CP even neutral higgs, and the Z0 gets the other CP even. Strange.
🙂 No, I’m not; in fact I got confused about this just last night as I was replying to your earlier comment, because indeed there are two contradictory intuitions, one that A0 should go to Z0, the other that h0 and A0 should form a multiplet. I hadn’t had time to check yet, so you may well be right. After today’s chaos passes, and assuming I find the same answer, I will correct the figure when time permits. Thanks! [Good ways to check; study U(1) and U(1)xU(1) before SU(2)xU(1).]
Thanks very much! Indeed it seems that some interesting exersices can be generated from here… I am also oscilating between both intuitions. On one side it is intriguing that one can built the mass degeneration mentioned here, on other hand it seems that MSSM does not allow to break electroweak symmetry without using SUSY-breaking terms. Which is puzzling by itself.
Hi Professor
I just saw that my original comment was published so you can delete this one. Thanks very much for the answer.
Depends on whether you want it to or not. Cold dark matter could have many sources.
One source would be a superpartner such as a neutralino, and in this case it would need to have a mass in the range that would be accessible to the LHC — and then if you assume all of the superpartners have masses in the same range, you’d come to this conclusion. And then you’d answer your question, “yes”.
But if you want to argue that there is no such support, you can do that too. You can point out that there are many other ways to get cold dark matter, and so to assume that a superpartner is responsible, and then argue that cold dark matter supports low-mass superpartners, involves circular reasoning… and thus the answer to your question is “no”.
I don’t think this debate is particularl useful. The only way to learn what dark matter is, and whether there is supersymmetry accessible at the LHC, is to run experiments.
Is there a recent review of the leading theories that explain cold dark matter without SUSY?
No review that I know of, but that’s because it is so easy. Any theory that has a new stable neutral particle can do the job.
Does the existence of cold dark matter also give some support to the super-partners having a mass measurable by the LHC?
Hello
A question: When you say that it solves the hierarchy problem you mean that SUSY (or SUSY breaking) explains why the EW breaks (via the Higgs) at such low scale? I.e. SUSY breaking drives EW breaking?
Hi — let me translate your comment for other readers:
your question is whether the solution to the hierarchy problem (see the new post, currently under “articles and posts/particle physics basics”, on this topic) that I refer to here has to do with whether supersymmetry causes the Higgs field to develop its non-zero value — whether there is a direct link between supersymmetry breaking, in particular, and the Higgs field having a non-zero value.
I am agnostic on this point (especially as far as what I said in the post) and I certainly haven’t explained this point enough for readers to follow. If supersymmetry turns up in the LHC data, it will probably be worth going into this level of detail in a public forum. But right now I view this as a pretty esoteric issue and would rather not get into it.
My main point here is that the hierarchy problem — the tendency for quantum mechanics to make the Higgs field be zero or enormous, rather than the comfortably tiny non-zero value that it has in nature — is mitigated by the presence of superpartners. Precisely how the Higgs field’s value is linked to superpartners and supersymmetry breaking is a longer discussion, and moot if supersymmetry turns out not to be a part of nature.