Today I continue with my series of posts on fields, strings and predictions.
During the 1980s, as I discussed in the previous post in this series, string theorists learned that of all the possible string theories that one could imagine, there were only five that were mathematically consistent.
What they learned in the first half of the 1990s, culminating in early 1995, is that all five string theories are actually little corners of a single, more encompassing, and still somewhat mysterious theory. In other words, after 30 years of studying various types of theories with strings in them, they ended up with just one!
On the one hand, that sort of sounds like a flop — all that work, by all those people, over two decades, and all we got for our efforts was one new theory?
On the other hand, it’s very tempting to think that the reason that everyone ended up converging on the same theory is that maybe it’s the only consistent theory of quantum gravity! At this point there’s no way to know for sure, but so far there’s no evidence against that possibility. Certainly its a popular idea among string theorists.
This unique theory is called “M theory” today; we don’t know a better name, because we don’t really know what it is. We don’t know what it describes in general. We don’t know a principle by which to define it. Sometimes it is called “string/M theory” to remind us that it is string theory in certain corners.
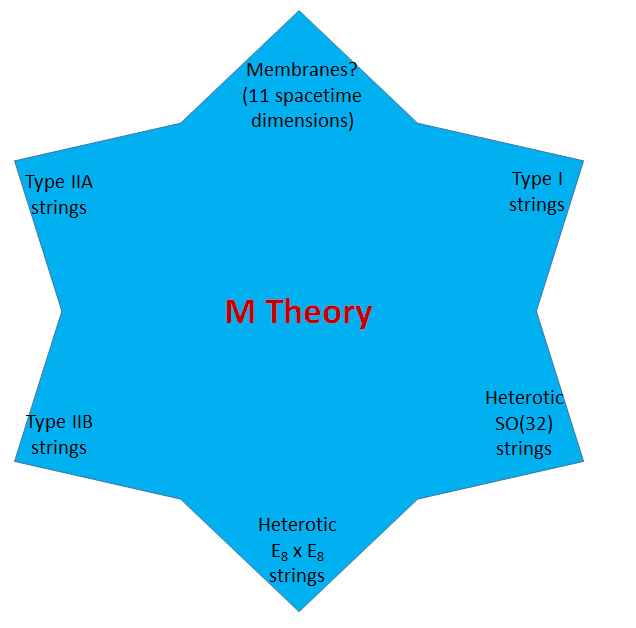
Note that M theory is very different in one key respect from quantum field theory. As I described in the second post in this series, “quantum field theory” is the term that describes the general case; “a quantum field theory” is a specific example within the infinite number of “quantum field theories”. But there’s no analogue of this distinction for M theory. M theory is (as far as anyone can discern) a unique theory; it is both the general and the specific case. There is no category of “M theories”. However, this uniqueness, while remarkable, is not quite as profound as it might sound… for a reason I’ll return to in a future post.
Incidentally, the relationship between the five apparently very different string theories that appear in M theory is similar to the surprising relationships among various field theories that I described in this post. It’s not at all obvious that each string theory is related to the other four… which is why it took some time, and a very roundabout route involving the study of black holes and their generalizations to black strings and black branes, for this relationship to become clear.
But as it did become clear, it was realized that “M theory” (or “string/M theory”, as it is sometimes called) is not merely, or even mainly, a theory of strings; it’s much richer than that. In one corner it is actually a theory with 10 spatial (11 space-time) dimensions; this is a theory with membranes rather than strings, one which we understand poorly. And in all of its corners, the theory has more than just strings; it has generalizations of membranes, called “branes” in general. [Yes, the joke’s been made already; the experts in this subject had indeed been brane-less for years.] Particles are zero-dimensional points; strings are one-dimensional wiggly lines; membranes are two-dimensional surfaces. In the ordinary three spatial dimensions we can observe, that’s all we’ve got. But in superstring theory, with nine spatial dimensions, one doesn’t stop there. There are three-dimensional branes, called three-branes for short; there are four-branes, five-branes, and on up to eight-branes. [There are even nine-branes too, which are really just a way of changing all of space. The story is rich and fascinating both physically and mathematically.] The pattern of the various types of branes — specifically, which ones are found in which corners of M theory, and the phenomena that occur when they intersect one another — is a fantastically elegant story that was worked out in the early-to-mid 1990s.
A brane on which a fundamental string can end is called a “D-brane”. Joe Polchinski is famous for having not only co-discovered these objects in the 1980s but for having recognized, in mid-1995, the wide-ranging role they play in the way the five different string theories are related to each other. I still remember vividly the profound effect that his 1995 paper had on the field. A postdoctoral researcher at the time, I was attending bi-weekly lectures by Ed Witten on the new developments of that year. I recall that at the lecture following Polchinski’s paper, Witten said something to the effect that everything he’d said in his presentations so far needed to be rethought. And over the next few months, it was.
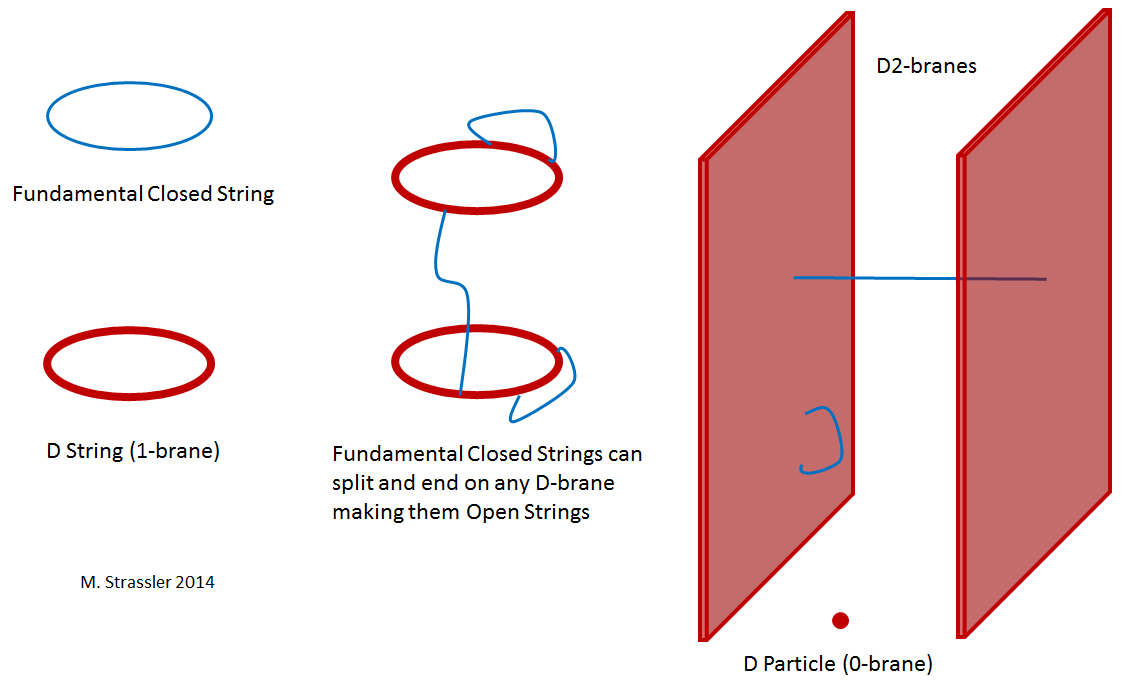
The fact that string/M theory is more than just a theory of strings is strikingly similar to something known about quantum field theory for decades. Although quantum field theory was invented to understand particles in the context of Einstein’s special relativity, it turns out that it often describes more than particles. Field theory in three spatial dimensions can have string-like objects (often called “flux tubes”) and membrane-like objects (often called “domain walls”) and particle-like blobs (“magnetic monopoles”, “baryons”, and other structures). The simplest quantum field theories — those for which successive approximation works — are mainly theories of particles. But flux tubes and domain walls and magnetic monopoles, which can’t be described in terms of particles, can show up even in those theories. So the complexities of M theory are perhaps not surprising. Yet it took physicists almost two decades to recognize that “branes” of various sorts are ubiquitous and essential in string/M theory. (We humans are pretty slow.)
Notably, there are contexts in which M theory exhibits no string-like objects at all. It’s the same with particles and fields; simple field theories have particles, but most field theories aren’t simple, and many complicated field theories don’t have particles. It can happen that the particles that would be observed in experiments may have nothing to do with the fields that appear in the equations of the theory; this was something I alluded to in this article. I also earlier described scale-invariant quantum field theories, which don’t have particles. Quantum field theories on curved space-time don’t have simple, straightforward notions of particles either. Quantum field theory is complex and rich and subtle, and we don’t fully understand it; I wrote seven posts about it in this series, and did little more than scratch the surface. String/M theory is even more complicated, so it will surely be quite a while before we understand it. But specifically, what this means is that what I told you in my last article about “simple superstring theories” is simply not always true. And that means that the first “vague prediction of string theory” that I described might not be reliable… no more than overall predictions of simple field theory, all of which are true in the context of simple field theories, but some of which are often false in more complex ones.
By the way, those of you who’ve read about string theory may wonder: where is supersymmetry in my discussion? Historically, in all these developments, the mathematics and physics of supersymmetry played an important role in making it easier to study and confirm the existence of these branes within string/M theory. However, the branes are present in the theory even when supersymmetry isn’t exact. One must not confuse the technically useful role of supersymmetry in clarifying how string/M theory works for a requirement that supersymmetry has to be an exact (or nearly-exact) symmetry for string/M theory to make sense at all. It’s just a lot harder to study string/M theory in the absence supersymmetry… something which is also true, though to a somewhat lesser extent, of quantum field theory.
To be continued… next, how are quantum field theory and M theory similar and different?



46 Responses
I like to mention Paco de Lucia’s guitar strings, together with Al Di Meola and John McLaughlin:
The Guitar Trio
Friday night in San Francisco
Passion, Grace and Fire.
“maybe it’s the only consistent theory of quantum gravity! ” I do not get this. Shouldn’t a self consistent quantum theory give at least an explanation of at least one of the cosmological enigmas such Dark Matter, Dark Energy or the fine tuning problem?
Once we understand it, it definitely could help. But first, we can’t calculate most things of interest in this theory yet. [We have a hard enough time calculating in quantum field theory, as I’ve emphasized in parts 4-7 of this series!] Moreover, we don’t know, right now, which of these enigmas that you’ve mentioned is actually due to quantum gravity! None of them, or all of them, may require the theory of quantum gravity; the explanations could all be due to unknown particles and fields, which might not be *uniquely* predicted by M theory.
I’ll address the fact that M theory, though it might be unique, doesn’t easily give unique predictions, especially for particles physics, in the next post in this series.
Can…..”the full string amplitude can be determined from the singular behavior on the boundary of the moduli space of the amplitude.” – http://xxx.lanl.gov/abs/1002.5029
http://2.bp.blogspot.com/-6v9ji1asUCw/UwOgN3LOaKI/AAAAAAAAI3U/5lmFyt52UQI/s1600/symmetry.jpg
looking back in time…….
and in case of the firewall, there can be no entanglement with regard to symmetry?
Just a quick clarification: you write ” the branes are present in the theory even when supersymmetry isn’t exact” but can they be present even in the absence of susy? Is there only a cutoff lenght or is the m-theory really independent from any sort of susy (experimental evidence…)
Well, this is tricky to say precisely.
The complete absence of supersymmetry in any part of the theory may well make the theory ill-defined. We just don’t know what happens in that case.
But supersymmetry that is invisible to our current and even far-future experiments, but which hides in extremely short distances and very high energies that are not currently accessible, can make the theory sensible. In that case, the branes clearly can still be there.
What is the clumping of space at planck scale in string theory ?
We know in both Newton’s and Einstein’s gravity predict that enough mass in a small enough space can produce a black hole. At quantum level the Gravity is negligble (where special relativity + quantum mechanics works well as relativistic QED) – but at planck scale level, the gravity is again prominent ?
Why the general relativity and special relativity in cosmic and quantum level cannot survive without rest mass ? – I mean, at planck scale it fails because of the rest mass ?
Is there any space time at planck scale ?
We assume that space-time at the Planck scale is discrete, quantised in Planck units and “qubitsed” (each pixel of Planck area encodes one qubit), that is, quantum space-time can be viewed as a quantum computer. Within this model, one finds that quantum space-time itself is entangled, and can quantum-evaluate Boolean functions which are the laws of Physics in their discrete and fundamental form. ?
I started reading this without my glasses on and read the first line as: “Today I continue with my series of poems on fields, strings and predictions” and thought – Oh God no! 🙂
Great article though!
😀
Maybe off-topic but just wondering your opinion of Max Tegmark’s ideas and if M-theory lays weight to the notion that physical reality is in essence just a mathematical object.
Umm… no comment. I haven’t read his book yet. M theory has nothing to do with it though, I think.
First, thanks a lot for your blog!
I saw David Gross in a recent talk saying that Quantum Field Theory is the same as String Theory. Well, if that’s true I guess it should be easy to prove, it’s mathematics, after all. What does he mean with that? is he saying they give the same predictions with different formulas or are they using the same formulas?
1) Yes, he’s correct. I’ll probably get to that in part 11 or 12; it’s far, far too subtle to explain in a comment, so please be patient. The fact that it’s true is why Juan Maldacena is famous, and it is also the basis of all of my work with Polchinski.
2) Who said mathematics is easy to prove? It took 350 years to prove that a^n + b^n = c^n, for a, b, c positive integers and n an integer greater than 2. It will certainly not be “easy” to prove string theory = quantum field theory. We haven’t even proven many of the facts stated here about field theory itself: http://profmattstrassler.com/2013/11/20/quantum-field-theory-string-theory-and-predictions-part-7/ But there is in fact an enormous amount of circumstantial evidence in a wide range of cases. For example, there are some field theories in which certain quantities can be calculated exactly; and those quantities can be compared with certain string theory calculations, and they agree. So much as I would like to prove it, or see someone else do so, I am not worried that it might turn out to be false.
Thanks for all the effort you put into these posts. I hope you will someday collect them into book form.
As a quantum/GR physics neophyte one thing I find confusing: you have, in this and previous posts, often said words to the effect, “we don’t fully understand theory ‘X’.”
I think I know what is meant when somebody says they don’t “understand” a phenomenon or a formula; I certainly know I don’t understand QFT or M theory, but when you say “we don’t understand” you imply no one, not even it’s creator(s), understands it.
In what sense can something be a theory that no one understands? I thought the purpose of a theory was to generate testable hypotheses on the basis of which parts of the theory were confirmed or not. If not, the theory would be modified to try and accommodate new results. My question is, how does one generate hypotheses from a theory one doesn’t understand?
Sometimes, a theory is “created” by someone in a clear form, with clear formulas that tell you how to do calculations. Those calculations can be very difficult, but if they’re in principle doable then the theory would still fit your intuitions. The five types of string theory are theories of this sort. In principle, they contain the necessary instructions to do calculations, even if in practice many such calculations remain out of reach.
However, in some theories the “creators” are making a conjecture based on how other theories interact. In the case of M theory, it was observed that the five types of string theory were related, as different limits of certain parameters. This is smoothing over some details, but basically when a force is strong in one string theory, the calculations give the same results as when the force is weak in another string theory. M theory asks the question: “What if the force is not weak or strong, but somewhere in between?” There should be a mathematical answer to that question, but you can’t just use the old rules for calculation from the string theories to figure it out. That’s the sense in which we don’t really understand M theory.
Matt can correct this account if he thinks I’m presenting parts of this incorrectly, this is just the best way I’ve found to explain it.
By the way, there are field theories that are similarly “not understood” in that we don’t know the starting point for the calculations, but we have reason to think the formulas should exist in some form. The (2,0) Theory (http://4gravitonsandagradstudent.wordpress.com/the-2-0-theory-where-does-it-come-from/) is another example.
Thanks very much. I didn’t appreciate that “theory” can describe a model which is formed of mathematical conjectures and is “tested” (sort of) by assessing how it interacts with other such theories.
Thanks also for the link to your page. I’m not at a level to understand it yet, but have bookmarked it for future reference.
This is a great question.
Often one gets hints that a theory must exist by doing a calculation that’s somehow partial and that suggests there’s a story to be told.
In the case of M theory, one thing that people discovered is that there were calculations they could do in Type IIA string theory which give exactly the same answer as calculations that they could do in 11 dimensional supergravity. Now, it was clear all along that these two theories are different; for one thing, one of them has strings running around, and the other has membranes, not strings. Yet for certain questions and in certain circumstances, they behave the same way. What’s the lesson of this and many other similar examples? That there’s a larger and mysterious mathematical structure which contains both Type IIA string theory and 11 dimensional supergravity.
A poor analogy (still looking for a better one): suppose you were dropped into Santa Monica, California and drove east; at some point you’d see the towers of a city. Now suppose you were dropped in Pasadena, California and drove south; again you’d see the towers of a city. Looking carefully, you’d realize they’re the same towers you’d seen east of Santa Monica. Now from this you might conclude that Santa Monica, Pasadena, and the city core that hosts the towers must be of a larger region that you had not previously realized existed. But only with more exploration, and perhaps the ability to fly over the area or climb a nearby mountain with a view, would you discover the greater Los Angeles area.
Why should we believe in string theory? NO SuSy, yet…NO KK-particles (resonances) yet, no Z’ yet, no extra Gauge bosons (yet), and after the LHC8 run…We have a stumbling absence of low energy SUSY, so naturalness seems to be “violated” in the sense SUSY is broken and low energy SUSY does seem to be responsible for the “light” 125 GeV Higgs-like (can we call it Higgs boson already) particle we have observed. So, in summary, beyond a relation between bosons and fermions, what are the motivations for Superstring theory from theory after the first LHC hit? I think it is important a constructive criticism some times is not seen for the most biggest defenders of the theory.
Well, let’s not mix apples and oranges. In general I agree with you, though in detail there are some errors in your comments. String theory does not predict anything so specific that you can just look at the LHC data and make statements about it; it’s more subtle than that. And your linkage of string theory with supersymmetry and extra dimensions is way, way too naive. In particular, your statement “So, in summary, beyond a relation between bosons and fermions, what are the motivations for Superstring theory from theory after the first LHC hit?” completely misses the point.
The motivation for superstring theory is simple; it’s the best candidate around for a theory that combines quantum field theory (which works for particle physics, including some parts of astronomy) with Einstein’s gravity (which works for astronomy, GPS systems, etc.) That’s been the best reason for almost 30 years, and still is.
Should you “believe” in it? I thought the whole point of modern science was that we didn’t go around “believing” things that we hadn’t checked experimentally. It’s a candidate to be taken seriously; it’s not a religion that you should have faith in.
Thank you, Matt. I have evolved from my “young ages” support of the (super)string (now M-theory, even when we have not managed a concrete definition-well, I lie, there are some “proposals”, but it is not the point I wanted to do) towards (perhaps) a more “solid” skepticism. Well, I did NOT say (directly at least) that string theory does predict the particles I quoted at the LHC scale. In fact, as a physicist myself, I am well aware (and some people soon “forget”) that, in principle, everything is calculable in string theory. Ironicanilly, the most mathematical and physical goodness of the theory has become its weakest link to reality. String theory itself is a theory that contains a finite (working) effective theory of quantum gravity (scattering of gravitons are finite in string theory) but the price to pay is how to fix the scale of the theory when we break supersymmetry. I have studied myself and in my master, and now, with a better knowledge of what the theory does, I have beome “feynman-ian” in the sense we have no way (at least not without problems) a clear way to break SUSY without generating a big vacuum energy AND flavor changing neutral currents that are now highly constrained by LHC data. That are the good/bad news. From the mathematical aside, string theory is “nice” (I have no doubt of that, since I am diverted myself with the odd theory of p-adic strings) but without supersymmetry found, the “super” version of string theory is experimentally put into trouble. I did not want to enter into a “belief” discussions…After all, when I tried myself to give some “constructive” reasons against superstrings in physics.stackexchange, I got I bunch of negative votes!!!! That is “religion”, the stringy version. I am aware of the merits of the theory (I would prefer the word model, just in the same way we should CALL Stantard Theory to the Standard model, but that is purely terminology, I know what I am talking about). The 100 TeV proposal (launched long ago in a famous talk by Nima-Arkami Hamed) is interesting, but the problem is the money at current time. The true pity is that muon collider technology is yet a few decade/s away from us :(, so, I currently think that the best bet to find new physics phenomena comes from the neutrino sector. We have good opportunities there, but big neutrinos detectors are complex too. Just a final curiosity, what do you think about the 7keV alledged DM signal? I think it could be as biased as the Fermi line, but we need more data.
With respect to string theory…Kaluza-Klein resonances, or good dark matter candidates (specially for WIMPs or similar), are OK with both SUSY and superstrings (dilaton, extra gauge-like fields,…), but again, my point is that directly, in the current formulation of string theory, we have no a concrete prediction, we can only explore “parameter spaces” (indeed as large as we want!!!). I suppose you will agree the landscape problem is also a big issue… 🙂
There’s nothing here that I strongly agree or disagree with… maybe too many things for me to grapple with at once. I don’t know what the universe is telling us right now, and the little hints of this and that are not very persuasive. So I think we have to keep helping our experimental colleagues, both by giving guidance and support with the measurements they are currently making, and by proposing new types of measurements that they might attempt.
wow how… diplomatic..
You always write clearly! But having read a little about string theory and having followed your posts on QFT, I feel a bit overwhelmed. And I wonder if your non-technical readers, for whom these posts are also aimed, have the same reaction?
These posts *are* among my most advanced, no question. We’re at the forefront of the field, here, and the air is a bit thin. I’m not exactly sure what I can do about it, but thank you for the feedback.
What are dimensions, (space)?
Fields interact with each over a distance, a space, does this mean if there were no fields there would be no space? Or does space create the fields, i.e. if the space between two fields tends to zero then two fields would either become 1 or cancel to 0.
One (1) of zero (0), there is a thought, could it be so simple? The ultimate quantization of reality, that infinitesimal instant in “time” when fields superimpose on each other, occupy the same space.
So what is time? Is time a measure of distance (space) where the fields turn from 0 to 1?
If 0-branes have a physical representation of particles what is the physical representation, if any, of strings and 2-branes?
What do you mean: “if 0-branes have a physical representation of particles”? That statement makes no sense in English and I can’t understand what you’re asking.
Are the particles mentioned in “Particles are zero-dimensional points; strings are one-dimensional wiggly lines; membranes are two-dimensional surfaces. In the ordinary three spatial dimensions we can observe, that’s all we’ve got.” distinct from physical particles?
We’re not talking about the real world here. We’re talking about what a theory (which may *not* be the real world) would predict for the possibly-imaginary world that it describes. I think when you say “physical particles” you might mean the particles observed in the real world. In the possibly-imaginary world that string/M theory describes, D0 branes are (generally very, very, very heavy) particles. However, the particles that are more similar to the ones out of which we ourselves are made may just be fundamental strings. Or they could even be D-branes of another sort, wrapped up on extra dimensions so that they appear like particles to us, the way a rubber band wrapped around a garden hose might look, from a distance, like a point on a line.
The range of possibilities for what real-world particles might be, if string/M theory actually describes the real world, is very great. I’m not going to be able to cover that issue properly.
“M theory is (as far as anyone can discern) a unique theory”
I think you should make clear that this is just a conjectural hypothesis, one that needs to be seen in the context of your accurate description of M-theory: “we don’t really know what it is. We don’t know what it describes in general. We don’t know a principle by which to define it.” The fact that 20 years of intense effort haven’t led to finding this “unique theory” should make one wonder whether something more complicated might be going on than a unique underlying theory with a moduli space of solutions. And, despite your “as far as anyone can discern”, not everyone is on board with the “unique theory” hypothesis. A good example is Tom Banks, see for example hep-th/0011255 which starts off with “I argue that isolated vacua of M-theory, cannot in any conventional way be said to live in the same theory as other disconnected parts of the moduli space. “
This is far too subtle an issue for a comment. As I wrote: “However, this uniqueness, while remarkable, is not quite as profound as it might sound… for a reason I’ll return to in a future post.”
In fact, there’s MUCH better evidence for caution with this uniqueness than the Banks paper that you mention.
I should have have said “fields existing in nature (whatever it means!) not just some mathematical fields you write down on a piece of paper!”
The best examples of such fields *in nature* arise in the description of physical materials right at the point of a “second-order” (i.e. rather smooth) phase transition. There, fluctuations in the fields occur at all scales, and the system is (roughly) fractal.
Is the difficulty of M-Theory just mathematical (i.e., the equations are too difficult so we have trouble using them to predict stuff) or is it more like the theory is incomplete and we don’t even know what parts are missing.
M theory is mathematically very challenging, so it is *possible* that it is incompletely known and there are missing parts. So the answer is: the first, and therefore possibly the second.
But stay tuned, I will explain more.
Very interesting article Matt. Question: If there are fields which do not show any particles, no matter what you do (whack them as you say!) won’t that break wave-particle duality of quantum mechanics?
Nope. For one thing, you’re mixing issues that don’t belong together; for another, particles are simply quantized ripples in fields (see my series http://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/ ) and the whole point is that you don’t have those types of simple ripples in such a field theory that has no particles.
So spinning fermions are not particles at all?
Sure they are.
Professor : where is the borderline between imagination and reality , or put it in another form ; why all that flying in imagination is not directed by OUR known reality ?
You must imagine many theories and their universes before you find the right one. I encourage you to read Alan Lightman’s “Einstein’s Dreams” as a literary expression of this notion.
Einstein did not dream , Einstein plagiarized his whole structure.