This post is a continuation of three previous posts: #1, #2 and #3.
When the Strong Nuclear Force is Truly Strong
Although I’ve already told you a lot about how we make predictions using the Standard Model of particle physics, there’s more to the story. The tricky quantum field theory that we run into in real-world particle physics is the one that describes the strong nuclear force, and the gluons and quarks (and anti-quarks) that participate in that force. In particular, for processes that involve
- distances comparable to or larger than the proton‘s size, 100,000 times smaller than an atom, and/or
- low-energy processes, with energies at or below the mass-energy (i.e. E=mc² energy) of a proton, about 1 GeV,
the force between quarks, gluons and anti-quarks becomes so “strong” (in a technical sense: strong enough that it makes these particles rush around at nearly the speed of light) that the methods I described previously do not work at all.
That’s bad, because how can one be sure our equations for the quarks and gluons — the quantum field theory equations of the strong nuclear force — are the correct ones, if we can’t check that these equations correctly predict the existence and the masses of the proton and neutron and other hadrons ( a general term referring to any particles made from quarks, anti-quarks and gluons)?
Fortunately, there is a way to check our equations, by brute force. We simulate the behavior of the quark and gluon fields on a computer. Sounds simple enough, but you should not get the idea that this is easy. Even figuring out how to do this requires a lot of cleverness, and making the calculations fast and practical requires even more cleverness. Only expert theoretical physicists can carry out these calculations, and make predictions that are relevant directly for the real world. Don’t try this at home.
The first step is to simplify the problem, and consider an imaginary world, an idealized world that is simpler than the real world. Since the strong nuclear force is extremely strong inside a proton, the electromagnetic and weak nuclear forces are small effects by comparison. So it makes sense to do the calculation in an imaginary world where the strong nuclear force is present but all other forces are turned off. If you put those unimportant forces in, you’d have a much more complicated computer problem and yet the answers would barely change. So including the other forces would be a big waste of time and effort.
Here we use an imaginary world as an idealization — a bit like treating the earth as a perfect sphere. Obviously the earth is not a sphere — it has mountains and valleys and tides and a slight bulge at the equator — but if you’re computing some simple properties of the earth’s effect on the moon, including these details will waste a lot of your time without affecting your calculation very much. The art of being a scientist requires knowing what you need to include in your calculations, and knowing what not to include because it makes no difference. In fact we do this all the time in particle physics; gravity’s effect on measurements at the Large Hadron Collider [LHC] is tiny, so we do our calculations in an imaginary world without gravity, a harmless simplification.
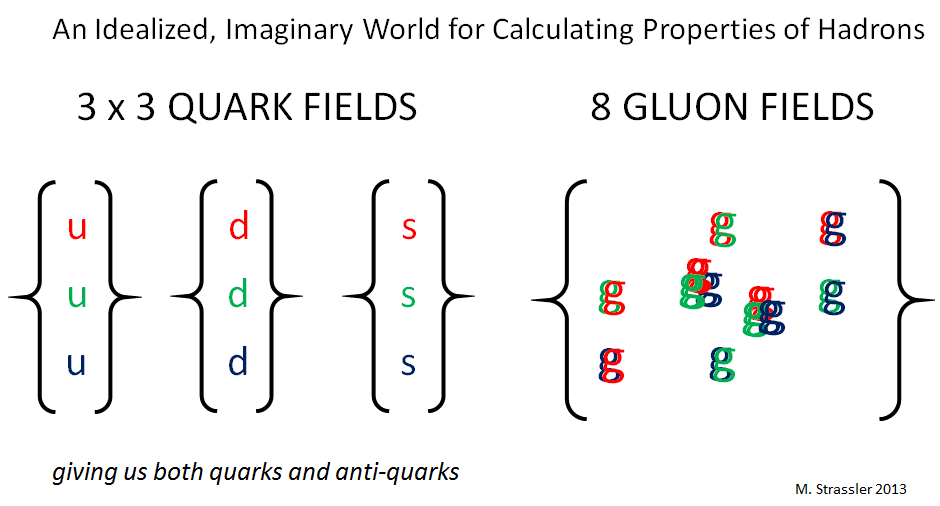
Here’s another idealization: although there are six types (often called “flavors”) of quarks — up, down, strange, charm, bottom and top — the last three are heavier than a proton and consequently don’t play much of a role in the proton, or in the other low-mass hadrons that I’ll focus on here. So the imaginary, idealized, simplified world in which the calculations are carried out has (see Figure 1)
- Three “flavors” of quark fields: up, down and strange, each with its own mass, and each with a charge (analogous to electric charge in the case of the electric force) which is whimsically called “color”. Color can take three values, whimsically called “red”, “green” or “blue”. These fields give rise to both the quark particles and their antiparticles, called anti-quarks, which carry anti-color (anti-red, anti-blue, anti-green);
- Eight gluon fields (each carrying a “color” and an “anti-color”.) [You might have guessed there’d be nine; but when color and anti-color are the same there are some little subtleties which aren’t relevant today, so I ask you to just accept this for now.]
So now we have a quantum field theory of three flavors of quarks with three possible colors, along with corresponding anti-quarks, and eight gluons which generate the strong nuclear force among the quarks, antiquarks and gluons. This isn’t the real world, but it is close enough to give us very accurate answers about the real world. And this is the one the experts actually put on a computer, to see if our equations do indeed predict that quarks, antiquarks and gluons form protons and other hadrons.
Does it work? Yes! In Figure 2 is a plot showing the experimentally measured and computer-calculated values of the masses of various hadrons found in nature. Each hadron’s measured mass is the vertical location of a horizontal black line; the hadron’s symbol appears below that line at the bottom of the plot. I’ve written the names of a few of the most famous hadrons on the plot:
- the spin-zero pions,
- the spin-1 rho mesons and omega meson,
- the spin-1/2 “nucleons”, meaning the proton and the neutron, and
- the spin-3/2 Delta particles.
The colored dots represent different computer calculations of the masses of these hadrons; the vertical colored bars show how uncertain each calculation is. You can see that, within the uncertainties of the calculations, the measurements and calculations agree. And thus we learn that indeed the quantum field theory of this idealized world
- predicts that hadrons such as protons do exist
- predicts the ones we observe, without a lot of extra ones or missing ones
- predicts correctly the masses of these hadrons
from which we conclude that
- the quantum field theory with the fields shown in Figure 1 has something to do with the real world
- we were wise to choose the imaginary world of Figure 1 for our study, because clearly the idealizations we made didn’t affect our final results to an extent that they caused disagreements with the real world
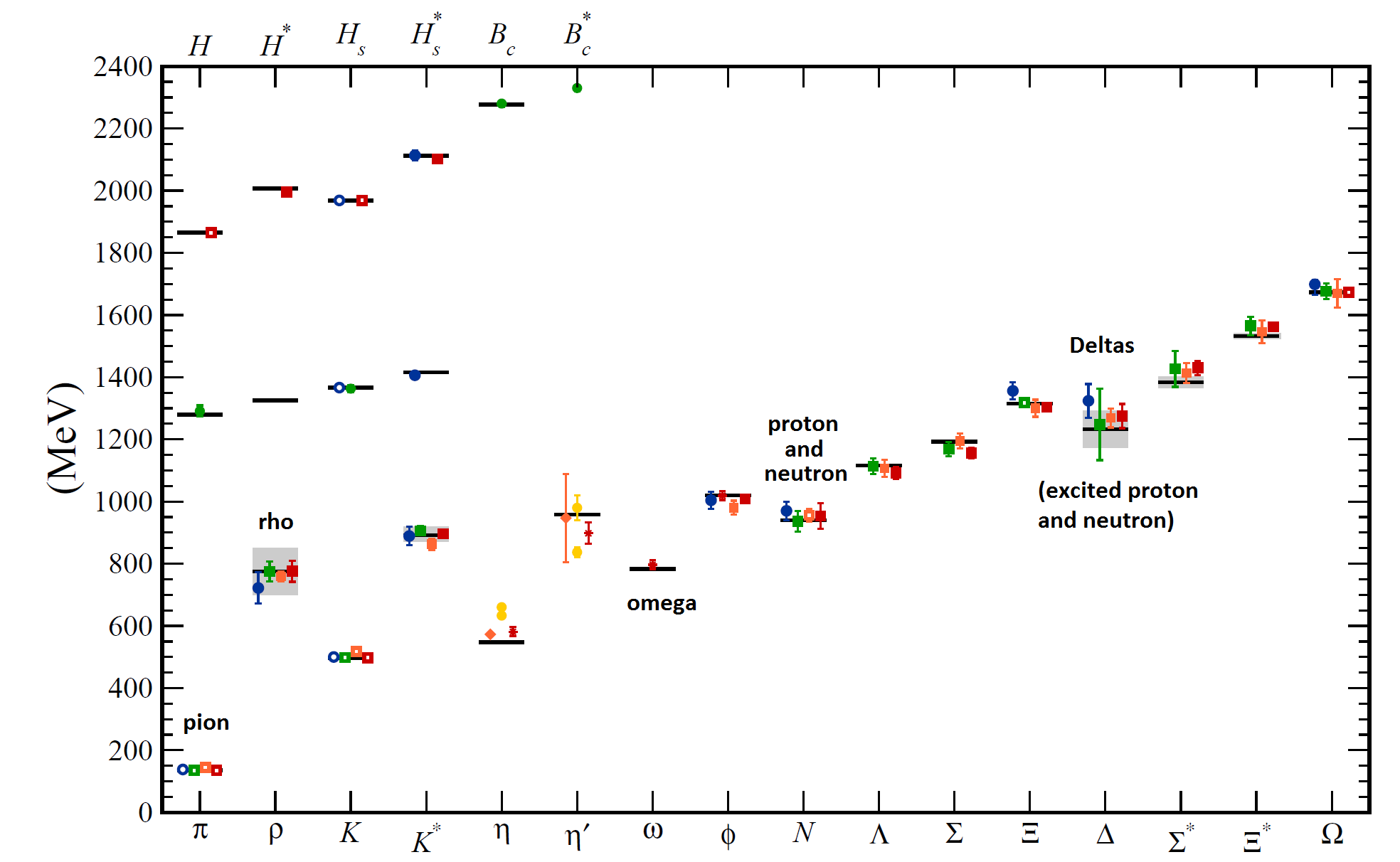
Fig. 2: The masses of various hadrons, whose names appear at bottom and whose measured masses appear as grey horizontal lines, as calculated by computer: each colored dot is a particular calculation, whose uncertainty is shown by a vertical bar. I have written the names of some famous hadrons.
All looks great! And it is. However, I’ve lied to you. I haven’t actually told you how hard it is to obtain these answers. So let me give you a little more insight into what you have to do to obtain these calculations. You have to go off into even more imaginary worlds.
How the Calculation is Really Done: Off In Imaginary Worlds
The imaginary world I’ve described so far is still not simple enough for the calculation to be possible. The actual calculations require that we make predictions in worlds very different from our own. Two simplifications have to do with something you’d think would be essential: space itself. In order to do the calculation, we have to imagine
- that the world, rather than being enormous, is made of just a tiny little box — a box only large enough to hold a single proton or other hadron;
- that space itself, rather than being continuous, forms a discrete grid, or lattice, in which the distances between points on the grid are somewhat but not enormously smaller than the distance across a proton.
This is schematically illustrated in Figure 3, though the grids used today are denser and the boxes a bit larger. The size of a proton, relative to the finite grid of points, is indicated by the round circle.
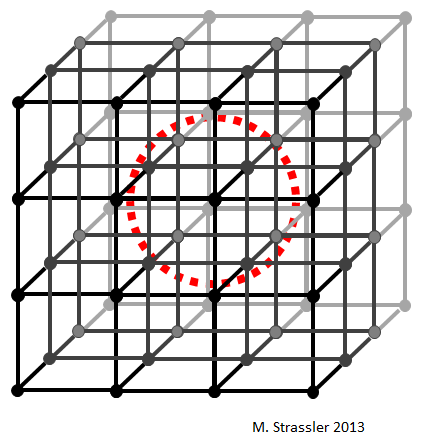
Advances in computer technology are certainly helping avoid this problem… the better and faster are your computers, the denser you can take your grid and the larger you can take your box. But simulating a large chunk of the world, with space that is essentially continuous, is way out of reach right now. So this is something we have to accept, and deal with. Unlike the idealizations that led us to study the quantum field theory in Figure 1, choosing to study the world on a finite grid does change the calculations substantially, and experts have to correct their answers after they’ve calculated them.
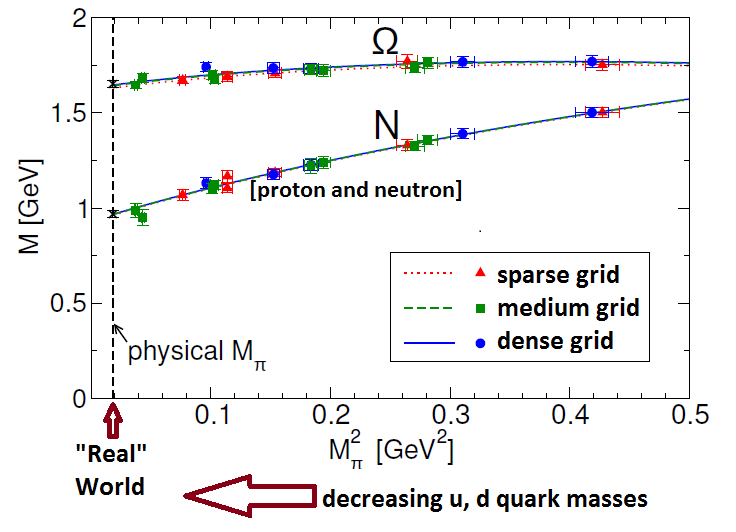
And there’s one more simplification necessary. The smaller are the up and down and strange quark masses, the harder the calculation becomes. If these masses were zero, the calculation just would be impossible. Even with the real world’s quark masses (the up quark mass is about 1/300 of a proton’s mass, the down quark 1/150, and the strange quark about 1/12) calculations still aren’t really possible — and they weren’t even close to possible until rather recently. So calculations have to be done in an imaginary world with much larger quark masses, especially for the up and down quark, than are present in the real world.

So since we can’t calculate in the real world, but have to calculate in a world with a small spatial grid and heavier quarks, how can we hope to get reasonable answers for the hadron masses? Well, this is another place where the experts earn our respect. The trick is to learn how to extrapolate. For example:
- Do the calculation for fields in a small box.
- Then do the calculation again in a medium-sized box (which takes a lot longer.)
- Then do the calculation in a larger box (still small, but big enough that it uses about as much computer time as you can spare.)
Now, if you know how going from a small to medium to larger box should change your answer, then you can infer, from the answers you obtain, what the answer would be in a huge box where the walls are so far away they don’t matter.
The experts do this, and they do the same thing for the space grid, computing with denser grids and extrapolating to a world where space is continuous. And they do the same thing for the quark masses: they start with moderately large quark masses, and they shrink them in several steps. And knowing from theoretical arguments what should happen to the hadron masses as the quark masses change, they can extrapolate from the ones they calculate to the ones that would be predicted if the quark masses were the real-world ones. You can see this in Figure 4. As the up and down quark masses are reduced, the pion mass gets smaller, and the “nucleon” (i.e. proton and neutron) masses becomes smaller too. (Also shown is the Omega hadron; this has three unpaired strange quarks, and you can see its mass doesn’t depend much on the up and down quark masses.) The experts take the actual calculations (colored dots), and draw a properly-shaped curve through all the dots. Then they go to the point on the horizontal axis where the quark masses equal their real-world values and the pion mass comes out agreeing with experiment, and they draw a vertical black line upward. The intersection of the black vertical and blue curved line (the black X mark) is then the prediction for what the proton and neutron mass should be in the real world. Well, you can see that the black X is pretty close, within about 0.030 GeV/c², to what we find in experiments: 0.938 and 0.939 GeV/c² for the proton and neutron mass. And this is how all of the results shown in Figure 2 are obtained: extrapolating to the real world by calculating in a few imaginary ones.
The Importance of Such Calculations
This is a tremendous success story. The equations of the strong nuclear force were first written down correctly in 1973. Calculations like this were just becoming possible in the mid-1980s. Only in the 1990s did the agreement start to become impressive. And now, with modern computer power, it’s become almost routine to see results like this.
More than that, these methods have become essential tools. There are many important predictions made for experiments which are partly made with the methods I described in my previous post and partly using these computer calculations. For example, they are extremely important for precise predictions of the decays of hadrons with one heavy quark, such as B and D mesons, which I have written about here and here. If we didn’t have such precise predictions, we couldn’t use measurements of these decays to check for unknown phenomena that are absent from the Standard Model.
But There’s So Still Much That We Can’t Compute
Despite all this success, the limitations of the method are profound. Although computers are fine for learning the masses of hadrons, and some of their other properties, and quite a few other interesting things, they are terrible for understanding everything that can happen when two protons (or other hadrons) bump into each other. Basically, computer techniques can’t handle things that change rapidly over time.
For example, the data in Figure 6 show two of the simplest things you’d like to know:
- how does the probability that two protons will collide change, if you increase the energy of the collision?
- what is the probability, if they collide, that they will remain intact, rather than breaking apart into a spray of other hadrons?
We can measure the answer (the black points are data, the black curve is an attempt to fit a smooth curve to the data.) But no one can predict this curve by starting with the quantum field theory of the strong nuclear force — not using successive approximation, fancy math, brute force computer simulation, string theory, or any other method currently available. [Experts: there are plenty of attempts to model these curves (look up “pomeron”.) But the models involve independent equations that can’t actually be derived from or clearly related to the quantum field theory equations for quarks and gluons.]
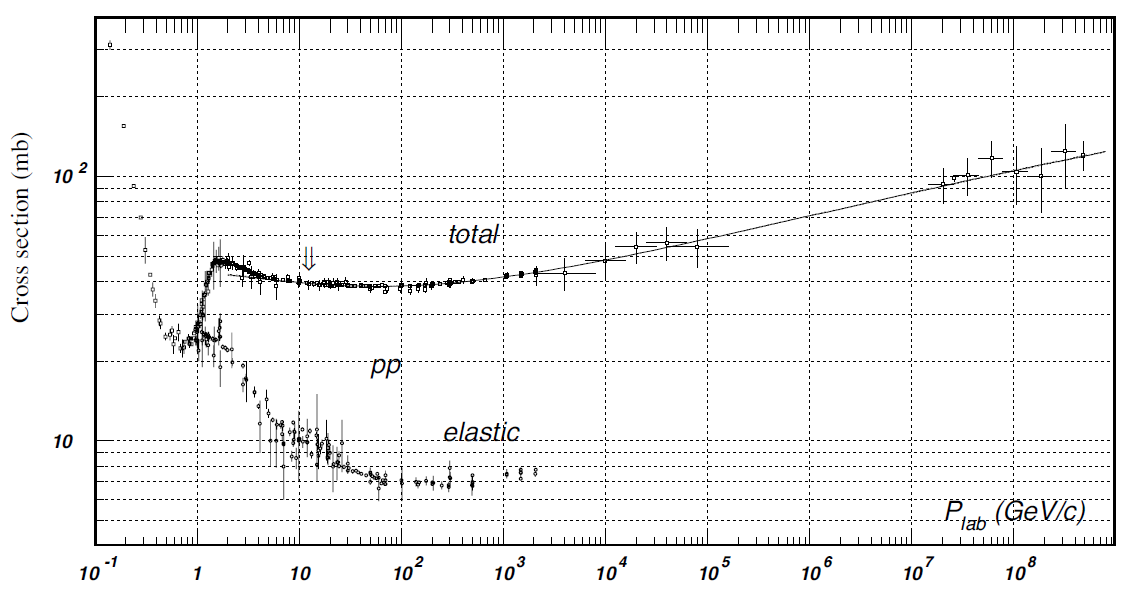
At the LHC, when a quark from one proton hits a quark from another proton, we can predict, using the successive approximation (“perturbative”) methods described in my previous post, what happens to the quarks. But what happens to the other parts of the two protons when the two quarks strike each other? We can’t even begin to predict that, either with successive approximation or with computers.
My point? The quantum field theory of the strong nuclear force allows us to make many predictions. But still, many very basic natural phenomena for which the strong nuclear force is responsible cannot currently be predicted using any known method.
Stay Tuned. It’s going to get worse.
Continued here…



73 Responses
Allow me to get this comment straight: when you say “This is always true for gluons”, it is my understanding that it is because gluons are the mediators of the strong nuclear force, which happens to be a strong interaction, is that right?
Yep, I know that.
We only know that the “neutral color” constraints apply, but there are still some degrees of freedom available for the actual number to be undetermined!
Let me be even more precise; the only quantity which is actually physically meaningful is the number of quarks minus the number of antiquarks. Quark number, antiquark number, and gluon number are not physical operators in the Hilbert space of the quantum mechanical theory; you simply cannot define them. This is always true for gluons, and true also for quarks and antiquarks once the forces involved aren’t weak. [It’s even true for electrons and positrons and photons if you imagine making electromagnetism into a strong force.] Even if you try, you will never find a physical system in which the number is specified.
Thanks a lot for the heads up!
So, it is the energy contents that is related to the mass of hadrons and we can’t actually predict the number of quarks, antiquarks and gluons inside a hadron, but it is my understanding that, no matter what the number is, the actual number of particles must follow the “neutral color” rules, right?
But the neutral color rule is very open — it requires only that n_quarks – n_antiquarks = 3.
I have a question regarding the “swarm” of quarks that compose the hadrons (proton and neutron) … It is my understanding that all those quarks moving within the proton or the neutron play a part in the determination of the mass of the proton and the neutron. My doubt is: the proton and the neutron have a very precise mass, so, how is it that that we can’t determine with some precision how many quarks are inside them?
Or is it that the mass of the proton or the neutron is undirectly related to the number of quarks inside them?
The numbers of quarks, anti-quarks and gluons in a proton are not quantum mechanically specified in a proton — in somewhat the same way that the position of an electron in an atom cannot be specified in the ground state of a hydrogen atom.
And indeed, the mass of a proton is related to the *energy* of the objects inside it — divided by c^2 — which is not determined by the number of objects inside it, or their masses.
The proton is complicated, and it isn’t just a bag of massive objects sitting in place. Everything inside it is whizzing around, colliding, appearing and disappearing… highly relativistic, and completely counter to your standard, non-relativistic, atomic intuition.
Does the proton model being used to obtain Fig 6 probabilities assume the type I believe you have described at an earlier time, where the proton has “hundreds” of various types of up and down quarks buzzing around within and simply has the slight over-abundance of having 2 up quarks and 1 down quark that thus leads to distinguishing this object from the neutron which has the alternate over-abundance feature??
I’m a little confused. Figure 6 contains data (the dots) and a model (the curve). If you are talking about how the curve was obtained, then the answer is “sort of, but the model is of a rather different sort…” The precise details of the quarks and antiquarks inside the proton aren’t believed to be relevant, because it is believed that the physics that dominates the total cross-section has to do entirely with the many gluons in the proton. (There is strong evidence from several sources.) In fact proton-antiproton cross-sections are almost identical, and it is expected (though we can’t actually do the experiment) that proton-neutron and neutron-neutron and neutron-antineutron etc. scattering cross-sections would also be essentially identical.
What makes the nuclear force so strong? What kind of charges are QCD [Quantum Chromo (chroma = color) Dynamics] charges? Are they anything like positive and negative charge of electromagnetic force? Meaning, do they attract, repel? Do they have parity that can swap according to what’s near it? I’m under impression that color charge operates on a principle of; I can be anything you want. Am I right? is this covered elsewhere?
Thanks for a really great series of articles. They’ve reminded me of a question I’ve wanted to ask for a while: What led to the acceptance of the Murray Gell-Mann quark model over Han-Nambu? I find non-integer charges somewhat unsettling when pitched against my chemistry background and so would love to know where they come from.
Regarding Fig.2, I couldn’t help but notice in the rho column a horizontal bar of ‘measured’ particles at a vertical level of 1325 MeV, but no computer predictions. And also a Green dot, some unspecified computer run, presuming ‘medium’ box, in the nu’ column, at the top of the vertical scale at a level of 2325 MeV. What can you tell me about these data points?
If the road from quarks to protons is so much in need of huge approximations , would you please clarify how the road from proton to quarks was crossed in the first place ?
Fascinating read. Thanks!
Two small typos I noticed:
1. Figure 4 should be Figure 5 here: “You can see this in Figure 4. As the up and down quark masses are reduced, the pion mass gets smaller …”
2. “So” and “Still” should be swapped in the header “But There’s So Still Much That We Can’t Compute”
As I understand it , an ontological QCD theory Must tell us why the dquark cannot decay to uquark in the proton , and what would happen if the proton was a uuu particle .
Einstein confused us with equivalence principle. Mass is intrinsic property like charge and we are explaining by Higgs mechanism through Higgs Boson based on standard model calculation …. The Higgs Boson ..CERN found is not STANDARD MODEL ..Higgs Boson. Let us see further in the days to come. So mass is intrinsic where as weight ,etc etc are phenomena . We should not be over joyed on HIGGS BOSON discovery. Even rest mass is a phenomena.
I’ll be honest and say that I do not understand your proposals. Primarily because you offer no justification. Although is my own opinion that the Higgs results are too flimsy to draw any conclusion.
Peter Higgs and Francois Englert.
“for the theoretical discovery of a mechanism that contributes to our understanding of the origin of mass of subatomic particles, and which recently was confirmed through the discovery of the predicted fundamental particle, by the ATLAS and CMS experiments at CERN’s Large Hadron Collider”.
But “rest mass” is phenomenological. It is like your are travelling in a car with confidence of not falling over – as if you are travelling on a Ferris wheel – which actually is (physical reality) !
What would happen if the grid is built with nodes separated by Planck,s length ? Are we entering here the regime of loop QG ?
How can I trust a math. Structure where it’s basic foundation is the expertise and smartness of he who handling it ? Isn’t this introducing the subjective in the fabric of the abstract ?
Are micro physics in a circular reasoning paradox ?
As for matching observations , how can I be sure that what you say IS the correct description while —-as you said —- many Math. Formulations can match observations ?
I am NOT attacking any one/thing I just want to understand.
But isn’t this a story of knowing proton size and mass then converging equations to meet what we know ?
For a real prediction I would imagine the theory to give from quarks properties the size and mass of the hadrons !?
Are we confident with ten sigma level that what we describe as the micro world is reality ? ,,,,,, now I doubt .
The Higgs (h) got its experimental identification because it is trapped inside the realm of electromagnetic field (QED), where “REST MASS” exists.
It is the angular momentum (scalar field) less than the speed of light. Unlike photons it is neither completely free from hadronization nor partially free like goldstone bosons (in weak force) ?
Why in QCD the experimental identification of scalar “Dilaton” is not possible because, of the “RELATIVE MASS” – due to the near speed of light of quarks and *gluons* ?
Computations work only where rest mass exists. Where relative mass (of gluons) exists, unlike the “constant” coupling constant α in EM field, a “dynamic variable” like “Dilaton” is needed – which need computation like weather forecast.
It will become more difficult if gravitational force grows stronger with further short distance – and computation become as hoax as evolutionary biology ?
Yes, my calculations also disagrees with such a nuclear strong force applicable for such a small distance and I have tried to get rid of it by a revised atomic model. I think we should work to see it further and may be those with higher mathematical skill can manage to explain further. Read my theories published in year 2002.
Good post! Thank you Matt.
Actually I got an inspiration from it. If (and when as usually) I manage to address mathematically my inspiration those presented calculation methods are replaced with much easier and accurate ones. How about that! 🙂
I found your organization of the information you conveyed on this complex topic wonderfully helpful. And I did not realize that there are processes that “we can’t even begin to predict either with successive approximation or with computers.”
Thanks!
In my experience it is an entirely different set of professional computer engineers that take physical equations like these and place them on to large-scale machines. If particle theorists are mapping their equations to hardware at LHC, I’m a little surprised that they have time for anything else.
Can you, or do you have pointers to, actual code and machine architecture documentation (or a machine model number if vendor provided)? It would be very informative for us (many of whom, I suspect, are more familiar with computation than mathematics) to see the actual computations, the code and the machine mapping, and the mathematics side by side.
What I note is that the models and equations suggested in this article are all mass/energy predictions and they say nothing concerning the trajectories of the particles. Since they are presumed to be independent of any consideration of gravitational mass, I assume they are thought to travel in straight lines.
This is why I asked earlier about gravitational compensation in the placement of LHC detectors (or words to that effect). Such fine compensation would potentially allow the measurement of the gravitational mass component – and the contribution to the particle mass could then be determined (easier said than done, no doubt).
So allow me to continue my questions from the point of view of naive GR
http://profmattstrassler.com/2013/10/01/quantum-field-theory-string-theory-and-predictions-part-3/#comment-89530
If the equivalence principle holds at the particle level and there is, indeed, the immediate binding of intrinsic particle mass/energy and gravitational mass (that together we should consider “inertial mass” – clarifying my earlier usage), suggested by the equivalence principle and my earlier remarks on the interpretation of GR, then it would be evident in these trajectories would it not? Just as, for example, the large mass of a train is steered by the relatively low mass of the rail (this is only a pedagogical example), or the earth is guided in its orbit around the sun (and presumably all the particles of which it is composed).
One might place an LHC detector in a distant stationary orbit, for example, to see if you get the same results.
I might add that speaking from the point of view of scientific structuralism (also called “structural realism”), it seems entirely plausible that gravitation (more precisely, the light field distortion mentioned earlier) is, in fact, the sole source of mass/energy in all of its forms and forces. And what we speak of as particles is simply structure.
Again, I like this view because of its epistemic simplification, naturally implied by Einstein’s advocacy of general covariance.
I am obviously taking enough rope to hang myself by, speaking as one attempting to build the bridge between pure mathematics and the physical sciences, so I hope that you will open the trap door soon if there is one … :-). If structure were the common subject of pure mathematics and physical science, as I suspect it is, it would help us all a great deal.
Prof. Strassler, I wonder why you did not mention another sense in which the world of the lattice QCD calculation is imaginary – in a double sense: A mathematical trick (Wick rotation) is used to do the calculation in a world where space and time coordinates look the same, as if there were just four space coordinates (and no time), which can be expressed as letting the original time coordinate take imaginary (now used in the sense of complex numbers) values.
Or is the Wick rotation a completely rigorous mathematical equivalence that does not need any heuristic physical assumptions, so it does not count as a simplification in that sense?
The Wick rotation is not specfic to lattice QCD-perturbative calculations in the continuum theory are also done using it. For the action of QCD and lattice QCD, involved in the calculations here, in fact, the Wick rotation leads to a mathematically well-defined framework.
On the other hand, for calculations that involve “real-time” dependent phenomena, it cannot be used and the calculations are correspondingly more complicated.
Yes, I also initially thought “imaginary world” referred to working in Euclidian space instead of Minkowski space..
This is a very interesting article, thank you. I had no idea how complicated the numerical calculations can be.
Just a question: are these things related to the “second and third layer” of discussion about nucleons, which you were planning to write about in April? Or this is a different issue?
The related article: http://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-structure-of-matter/protons-and-neutrons/
Matt. You just gave me the impression that QFT is a retrodiction not really prediction theory !?
The sympathetic explanation for non experts from Professor,
I understand…. the garvitational, EM, weak forces were left outside the small box of proton size becaz, the strong force is much stronger in small distance. The fine structure constant is measurable to bridge the continuous electromagnetic field in QED. But zooming the space in much shorter distance of strong force, the “vacua” need much more bridging (lattice) like planck mass or “Dilaton” – becaz uncertanity increases ?
Along with the shortening distance, rest mass is cease to exist up to the realm of electromagnetic force (photons), relative mass cease to exist up to the realm of strong force. But gravity and angular momentum of gluons grows stronger as distance shortens. No more hadronization and mathematics (numerical fields) irrelevant here ? – compared to the detachment of photon field from proton and electron.
Gravity is negligible only at proton size, at much shorter and much longer distance it influence ?
The solution of brutal computation to bridge the anthropic landscape is like bridging the missing link with “evolutionary biology” ?
Matt: has anybody tried to do anything like this to calculate electron mass?
The electron isn’t (so far as we know) a composite particle; so, there’s nothing to calculated it from.
*calculate
To calculate the electron’s mass you would need to perform the corresponding calculation in the electroweak sector. This sector is a consistent quantum theory only when you include, along with the electron and its neutrino, the up and down quarks–they too have electromagnetic and weak interactions. In fact just how to set up the calculation to do using numerical simulations is much harder than studying the effects that are described here.
OK noted guys.
Can anybody give me the name of a guy or group actively working on lattice QCD?
This is a good starting point: http://www.latticeguy.net/lattice.html
Thanks Stam.
How can it be harmless simplification? The entire dark energy effect also ignored. We do not have right physics and mathematics with powerful computer to go beyond standard model but we are acknowledging our limitations and understanding the defects in the vision of Einstein or even with the models of present Atomic theory . Durgadas Datta predicted a model without strong force because the calculations showed that a strong force of such dimension is impossible to exist on the vicinity approach. Kindly read the theories published in year 2002…
Dark energy is utterly irrelevant at the scale of particle interactions. For that matter, it’s irrelevant at the scale of the whole collider, or the planet, the solar system, or even the entire galaxy. It’s only on intergalactic scales that the aggregate effect of dark energy becomes measurable.
Imagine if Newton had been hit upon the head by an innocent small apple, had the glimmer of his great ideas and then sat back down, shaking his head, saying “Nah …”
Very interesting articles on a very complex subject, thank you Prof.
Interesting curve, (Fig. 6). If you continue the linear part of the curve (slope of about 15-20 degrees) to the intersecting point, (24 mb & 1 GeV/c), it is basically a 1st order disturbance, (only one overshoot) which means a very highly damped system. Does it mean then if you tilt the axis of the chart and workout of energy (x-axis) and cross section (y-axis) to coincide with the curve one deduce the equation(s) for mb vs Gev/c? Like breaking through a sphere with a very high viscous shell.
Could the overshoot part of the curve be an indication of the strength of the nuclear force(s)?
Dear Matt, is it known why (in the SM) the down quark is stable inside the proton?
I keep finding on the Internet: because the proton is the lightest particle with 3 quarks but that is circular reasoning. Anyone?
The short answer is that the down quark transforms into an up quark by weak interactions, which are neglected here.
In fact, whereas the strange quark is lighter than the charmed quark and the bottom is lighter than the top, the down quark is *heavier* than the up quark-and this leads to the fact that the neutron is slightly heavier than the proton and, thus can decay (through weak interactions). Were the down quark, also, lighter than the up quark, the neutron would be stable and the proton would decay-and a lot of things would be very different…
Of course, if you don’t take into account weak interactions the down quark can’t decay! My question is more general. If you take the full SM (electroweak and strong) into account, is it clear why the proton is stable? The fact that the down quark is heavier means that in principle it can decay to an up quark but for some reason 3 up quarks don’t form a composite particle. Even if three up quarks can’t respect Fermi statistics you still have to assume composite particles are white which (correct me if I’m wrong) is still not clear from first principles. Since proton decay is an issue in many BSM models it should at least be known what can be expected in the SM.
In the Standard Model the proton is stable because of conservation of baryon number. It appears that if you look at all interactions that involve hadrons made of three quarks (or antiquarks)–these are called baryons–the number of baryons is always conserved. Since the proton is the lightest baryon, it can’t decay.
Three up quarks respect Fermi-Dirac statistics, thanks to the fact that they carry color charge–in fact that was why it was introduced, before QCD was invented. And these particles have been observed: they are the so-called Delta resonances.
“It appears … the number of baryons is always conserved.” As baryons are composite particles this should follow directly from quarks and QCD (and maybe electroweak theory) Thanks for referring to the Delta resonance, I was looking for that name. I then saw it is heavier than the proton, so the proton can’t decay to it and that will have something to do with it. Then the strong interaction forbids the decay via the weak interaction and it must be an interplay between QCD and the electroweak force. Not an easy thing to show directly from within the SM it seems
Marcel,
“The short answer is that the down quark transforms into an up quark by weak interactions, which are neglected here.” Was that a satisfactory answer Marcel? Is telling you that d-quarks are unstable (even inside the proton) explain why the proton is the lightest baryon?
While it’s true that under certain conditions (even inside the proton) a d-quark can transform to a u-quark and a W-. The W- in turn transforms a nearby u-quark into a d-quark. This of course does not change the overall ‘chemical’ composition of the proton as uud anymore than gluon exchange which may change a blue quark to a red one, so long as a nearby quark is changed from red to blue has any overall effect on the fact that the baryon remains color-neutral or white. Thus your question remains a valid one.
Notice, as Matt points out, that even though the rest energy of the d-quark is ~2 x that of the u-quark, the u and d-quark have only a small fraction of the total rest energy of the proton (~4 MeV compared to over 900 MeV). This being the case there is no guarantee that the quark combination uuu will be less energetic than the combination uud – and in fact it is not. In reality and by qcd lattice calculation uud (the proton) is the least energetic baryon (3 quark combination). With ddu (the neutron) coming in a close second.
If you ask the further question as to why the proton is stable? Why can’t it decay into a positron and a couple of photons for example? They (meaning the vast majority of physicists) will tell you that given enough time (10^34 years) that that is exactly what happens; the proton decays. Proton decay has never been observed, and I myself prefer an old ‘explanation’ called Conservation of Baryon Number. But that’s another story…
Baryon number conservation can be seen to follow from the structure of the Standard Model, in terms of quarks and the gauge fields of the strong and electroweak interactions.
This is a subject that can, in principle, be addressed by lattice calculations, but which is very hard, in practice. Not only due to computational aspects but due to the fact that we don’t yet know how to set up the calculation in an efficient way.
Dear S.Dino and Stam,
Thanks to both of you for responding to my question. The overall picture is clear. The uuu combination is more energetic than the uud combination even though the uuu quarks rest masses (actually the Higgs masses) are lower. The d quark “knows” this QCD end result and cannot decay weakly to a u. Interesting isn’t it!
The statement relating the instability of the d-quark with the fact that the proton is the lightest baryon relates two distinct things, which I didn’t do.
What I said was that the d-quark can transform into a u-quark by weak interactions, which is the way the neutron decays. Since in Matt’s article weak interactions are neglected any such processes can’t occur.
Now the neutron can decay into a proton (and electron and electron-anti-neutrino) first, because the neutron is heavier than the proton, next because all, other, known conservation laws permit it. In particular the conservation of baryon number: both neutron and proton are baryons. Therefore that the neutron is more massive than the proton is a necessary condition for it to be able to decay into a proton-it’s not sufficient.
It’s an experimental fact that the proton is the lightest baryon. Therefore, as long as baryon number is conserved it can’t decay. This isn’t an empty statement, because there do exist other baryons than the proton and neutron and in their interactions baryon number is observed to be conserved, as well.
The fact that it’s slightly lighter than the neutron can be understood by the fact that the down quark is slightly *heavier* than the up quark (the proton has two u’s and an anti-d and the neutron two d’s and a u). Lattice calculations that could provide insight into this issue ar extremely hard to do the lighter the quarks.
Correction: the transformation of the d-quark into an up quark by *weak* interactions describes the *decay* of the neutron into the proton. Weak interactions are responsible for the decay.
Have any simulations been done on the scale of quarks or gluons? Maybe pong a gluon at a quark in 64x64x64?
Dear Professor, I was struck by “we do our calculations in an imaginary world without gravity, a harmless simplification.” I believe this is necessary and safe as you describe. In the same way, engineers usually do their calculations in an imaginary world without relativity.
The interesting times are when we discover that we were simplifying when we shouldn’t have been. Can’t avoid that trap, though, can we?
Fig. 2 calculation is certainly impressive with all the computer limitations. Questions :
(1) How many parameters and which ones , other than the three quark masses, you need?. Also if these quark masses (inputs) are used for predictions of other cross sections then they would be extra successes.
(2) Is Pomeron consistent with ST?
Thanks.
Hypothetically, if you got a super magical computer infinitely more potent than what we have now, would this solve the problems you outlined? With this hypothetical supercomputer, would you be able to perform the simulations in a continuous space, without the lattice?
@Ostrololo: having more powerful computers is one part of the solution to this problem, but these kinds of problems are not entirely solvable with just more computing power available.
Over and over again scientists discover by chance new “tricks” on numerical methods that are much more important and useful than having more powerful computers.
For instance, the modern version of Monte Carlo Method was deviced by Ulam in the 1940s as a way to solve math problems with the kinds of limited computing power available at that time.
It was later realized that the Monte Carlo Method was able to calculate an approximate value of a math problem with a smaller accumulation of errors of approximations than other numerical methods, like say, to calculate an integral of a function in a hypervolume (a function with more than 3 dimensions).
Why can’t these calculations be performed on the paper? The process must be simple, only; without other elements (EM force, dark energy) one would not get a realistic picture of anything. What I would propose is; form groups of mathematicians. Give each group a specific calculation task. Finally, have a group of physicists and a few top mathematicians as a separate team and consider the results and how these fit with the theory. If they match, the theory predictions are very close to how things work, if not then perhaps theory needs teasing out a bit. Allow for an element of surprise. Above all, be patient and happy with you own contribution to science. The privilege of rounding off the M-theory may fall into the lap of the next generation of physicists, who will have much better technology (nano-computers) with which to solve these puzzles.
No. Continuous spacetime has an uncountable number of degrees of freedom. If you want, or need, to calculate some quantity using any computer, you need, at least, to be able to count. The limit of a continuum spacetime is just that-an extrapolation. However it’s not just a question of faster processors or faster and larger storage. For treating time-dependent phenomena, for instance, more efficient numerical techniques are needed-and this is, one, open issue.
Monte Carlo Method, maybe?
Indeed. The calculations involve integrals over so many variables that the only way to calculate them is by trying to generate independent samples (configurations) of gluon fields and quark fields, that contribute the most to these integrals. So it is a Monte Carlo method. The bottleneck of the calculation is taking into account the quantum effects of the quarks.
The grid for the calculations that is mentioned: is it somehow related to a finite element method grid? or is it some other kind of numerical method involved?
Kind regards, GEN
It seems that lattice gauge QCD computations are about where numerical weather forecasting was in the early-1980’s*. Is the problem in doing things like proton-proton interactions merely because of a lack of CPU cycles (i.e., it could be done, but it might take decades or longer to get a meaningful answer), or are there more fundamental issues that have to be addressed in numerically simulating interactions?
*Dealing with quark masses reminds me a little of how NMF addressed mountain drag, which is dominated by stuff going on well below the lattice grid scale.
I am not an expert (so I should probably just shut up) but I would suspect it’s a combination of both theoretical and numerical difficulties.
From a numerical standpoint, I would assume that the time needed for a calculation scales by at least the 4th power of the grid size; If your grid spacing halves, so you go from a 4x4x4 grid to an 8x8x8 grid, you have 8 times as many cells to compute, but it’s also likely that your delta-t (clock tick between simulation rounds) will also have to halve, leading to twice as many iterations, so a total of 16 times the computations. It could be worse, though, because the potential number of pairwise interactions between the grid cells rises as the square of the grid cells, so halving the mesh size could raise the number of cells by a factor of 8, and the number of interactions by a factor of 64, and if the delta-t also halves, the total processing by a factor of 128 (or 7th power). Since the strong force does not rapidly go to 0 with increased distance, it’s likely that this 7th-power case is involved.
From the description, it also sounds like the mass of the the up/down quarks enter into the situation in the denominator somewhere, so that zero mass would yield a divide-by-zero. I can think of two ways where a small mass could cause a problem: (a) it could be involved in the calculation of delta-t, so that a smaller mass yields a smaller delta-t, and thus more calculation time, or (b) it could cause numerical instabilities because of the limited precision of the calculations. Or both, which could be really bad. Increasing the precision of the calculations can help some, but is tricksy and takes more processing power (80-bit floating point precision is baked into most hardware and is relatively fast; doing more in software is slower, and not as well tested). But numerical instability is worsened when you do repeated calculations, so if smaller masses increased numerical instability AND increased the necessary number of iterations, then even with increased precision (and the increased time that implies) could yield a worse result. Recovering from that might require a smaller lattice (see previous paragraph) or even slower numerical calculations.
When you use any kind of numerical method, there is a host of mistakes you have to make sure that your algorithms avoid to commit.
For instance, want to avoid to calculate with very small decimal numbers (that leads to many kinds of root causes for errors in your calculations), so, you do not want to have differences (substractions) of very close numbers (the end result of such a substraction is a very small decimal number), or divisions that will lead to very small decimal numbers.
So, you try all sorts of tricks, like say, changing the numerical scale for your calculations by dividing your equations by some selected constants, constants that are “natural” to the problem at hand.