MATT STRASSLER
Of Particular Significance

The Strengths of the Known Forces

Matt Strassler [May 31, 2013]

In this article I want to discuss basic properties of the forces that we know about — four that we’ve actually observed, and a fifth — a new one — whose existence we infer from the discovery of the Higgs particle.

Specifically, I want to discuss what particle physicists mean in describing forces as being weak or strong.  It’s terminology that you’ll often see, but unless it’s been explained to you, there’s no way to guess what’s actually meant.  So here’s an explanation… a long one, but I hope it will give you many insights into how nature works, as well as raising more questions I’ll have to answer later…

“Weak” versus “Strong”

What do these terms mean?  While in ordinary life you and I would think of a strong force as one that can pull us off our feet and a weak force is one that we can counter by stiffening our muscles a little, that’s not what particle physicists mean at all.

By “strong” and “weak”, particle physicists are not talking about whether a force is absolutely strong, or absolutely weak. It’s not about whether the force could break a window, or hold up a bar of gold. “Strong” and “weak” in this context are semi-absolute terms, in a sense that we never use in daily life, or even in undergraduate physics classes. It’s a way of talking that only emerged from a deep understanding of quantum field theory, the modern mathematical language used to describe the known elementary particles and forces. But it’s fundamental to the way particle physicists think about these issues today. So I’m going to start by explaining the rationale behind this way of talking.

Take two objects of some type, perhaps elementary particles, and place them a distance r apart.  Suppose each exerts a force F on the other.  Then we will say this force is weak if

  • F is much less than (h c / 2π r² )

where h is Planck’s quantum mechanics constant and c is the speed of light.  Often it is convenient in physics to use not h but

  • ℏ = h / (2π)

In short, for particle physicists,

  • a weak force has F r² much less than ℏ c  
  • a strong force has F r² about as big as ℏ c  

[We don’t generally encounter forces, even in our theoretical studies, that are much stronger than (ℏ c / r² ); typically such strength makes them so complicated that we end up thinking about them in a different way.  Long story.]   This is a measure not of whether the force is weak in an absolute sense, but whether it is weak or strong compared to typical forces that are to be found at a distance r.  The question isn’t about the force; it’s about the force times the distance-squared, and whether that is smaller than or comparable to ℏ c.

To explain why this notion of strength is useful, I’ll illustrate the concept in the case of electromagnetic forces acting on simple charged particles, such as electrons, anti-electrons [“positrons“]  and protons.  Electrons have electric charge -e; protons and positrons have charge +e.

First, imagine two stationary protons, each with mass m and electric charge +e, a distance r apart. The electric force between them pushes them apart and has a strength given by the following formula

  • F = ke2 / r2

[What is k? see below…] The same formula would apply for two electrons, which both have electric charge -e. For an electron and a positron [an anti-electron, with charge +e], the force would have the same size, but would pull them together instead of pushing them apart.

Now — what is k? It’s called Coulomb’s constant, and what its value is depends on how we define e, the basic unit of charge. But it won’t matter, because in discussing electric forces involving elementary particles, we’ll always see ke2 appearing as a group, together. So we don’t need to know how big k is; we only need to know, how big is ke2?

It turns out that if r is larger than a millionth of a millionth of a meter, then ke2 is approximately 0.007 times (h c/2π), where h is Planck’s quantum mechanics constant and c is the speed of light. So we may write the electric force, times r² as (approximately)

  • F r² = 0.007 ℏ c

Since 0.007 is much less than 1, electromagnetism is a weak force, and remains so at all distances, down as far as we have measured.

It’s very mportant not to get confused here!  Just because electromagnetism is a weak force in this sense doesn’t mean that the force between two protons is weak in an absolute sense.  In fact, the electric force trying to push the two protons in a helium nucleus apart is comparable to the weight of a truck!  All that force acting on two tiny tiny particles!!!  But still, this is, for such a small distance, a rather weak force, and indeed a somewhat stronger force (the “residual strong nuclear force”) counteracts that electromagnetic repulsion, and holds the protons and neutrons of the helium nucleus together.

By the way, there’s a historical name for this number 0.007; it’s called the “fine structure constant” (because it sets the size of little differences in the energies of various configurations of atoms) and it’s normally called “α”:

  • α = ke2/ ℏ c = 0.007 297 352 57

It’s one of the most precisely measured quantities in nature. Often people write it as approximately 1/137 (and many decades ago various people thought maybe there was something special about the number 137), but if you’re going to do that really it should be written as 1/137.0359990…

Ok — so why is the fact that α is much less than 1 an indication that this force should be thought of as weak rather than as strong?

Why α«1 means the electromagnetic force is weak

This is best illustrated in the case where the force is attractive, as it is for the electron and positron, or the electron and proton.  The electron and positron are a little easier to start with, because they have equal mass m; they form an atom-like state called positronium, analogous to a hydrogen atom formed by an electron and proton, but more symmetric, with the two particles orbiting each other, rather than in hydrogen, where the electron orbits the nearly stationary proton. In fact, the formulas for hydrogen, for those who know them, apply to positronium too, with some minor changes (factors of 2) in a few places.  (Yes, the electron and positron in positronium eventually annihilate and turn into two or three photons, but only after the particles have orbited each other many billions of times — which admittedly only takes a tiny fraction of a second.)  For positronium, in its lowest-energy state,

  • the typical speed of either particle is α/2 × c
  • the typical motion-energy (i.e. “kinetic” energy) of either particle is  mc² × α²/8 .
  • the interaction-energy (or “potential” energy) of the two particles is –mc² × α²/2.
  • the binding-energy B of the positronium state (the sum of the motion-energy and the interaction-energy) is mc² × α²/4.
  • the mass-energy of the positronium state 2 mc² – B; and since the latter is much smaller than the former, the mass of the atom is just a tiny bit smaller than the sum of the mass of the electron and of the positron.

In short, because α is much less than 1, there are three essential and related facts

  1. The electron and positron move at speeds slow compared to the speed of light c.
  2. Kinetic, potential and binding energy B are all small compared to the electron’s and positron’s mass-energy, E = mc2.
  3. The mass of positronium is very close to the sum of the masses of the electron and positron.

All of these statements would be true no matter how large or small were the electron’s mass; they depend only on α being small.

Together these facts mean that in describing this atom-like state, Einstein’s theory of special relativity is not important; Newton’s laws of motion are good enough to make predictions, up to details that are no larger than α, i.e. to about the 1% level or better. And as we’ll see in the next section, this means the system is relatively simple.  It can be described using quantum mechanics, which has rather simple mathematics, without need for quantum field theory, which would be necessary if Einstein’s relativity were important.  The math for the hydrogen atom is the same as for positronium, and it is so simple that physicists learn about it as undergraduates, early in their first quantum mechanics class.

There’s another useful, though a bit less familiar, way to think about this.  We should remember that electrons, like all elementary “particles”, are really “quanta”, tiny ripples in quantum fields. They are more like waves than they are like little balls. Consequently they vibrate, as all waves do: they have a “frequency” of vibration. And the time it takes between one vibration and the next — which I like, poetically, to call a particle’s “heartbeat” — is equal to h/mc2. If α is small, then the time it takes light to cross the atom-like state is much larger, by 1/α, than the heartbeat of the particles that it contains. In this sense, positronium is relatively big.  And since the particles themselves travel much slower than light, it takes even longer for the particles themselves to cross the atom-like state, something like 1/α² heartbeats.

Other things that could have been complicated are rather simple too, when α is small. For instance, the force exerted by the positron on the electron can cause the electron to become, sometimes and briefly, a virtual electron and a virtual photon. (Virtual “particles” aren’t particles; a real particle is a well-behaved ripple in quantum fields, but a virtual particle is a more generalized disturbance of those fields.) But that’s rare, if α is small. Even rarer, the virtual photon will itself be disturbed into becoming a virtual electron and a positron.   Since there isn’t nearly enough energy around to make another real electron and positron, which would require energy of 2mc2 to come from somewhere (recall the motion and interaction energy are much less than this), it is very rare to make a virtual electron and positron. The fact that virtual particles are rare is why we can say so simply that “a positronium atom consists of an electron and a positron” — that’s indeed what it is, most of the time. Only in high-precision calculations do we need to be more careful, and remember that’s not always quite true. The same is true of a hydrogen atom: it is (almost all of the time) just one electron and one proton, held together by a simple electric force.

You can read about atoms here, where my descriptions are relatively simple.  In this article I partially explained how the hydrogen atom’s size can be inferred from quantum mechanics principles, and you can use that result to see why the speed comes out to be αc, and why the motion-energy and interaction-energy come out to be ½ mc² α².

What would happen if α were closer to 1?

But now imagine making α gradually larger and larger, increasing toward 1. What happens to positronium? [I must warn you what I’m about to describe isn’t a rigorous discussion! Those of you who are planning to be experts someday need to be more careful than I’m about to be.]

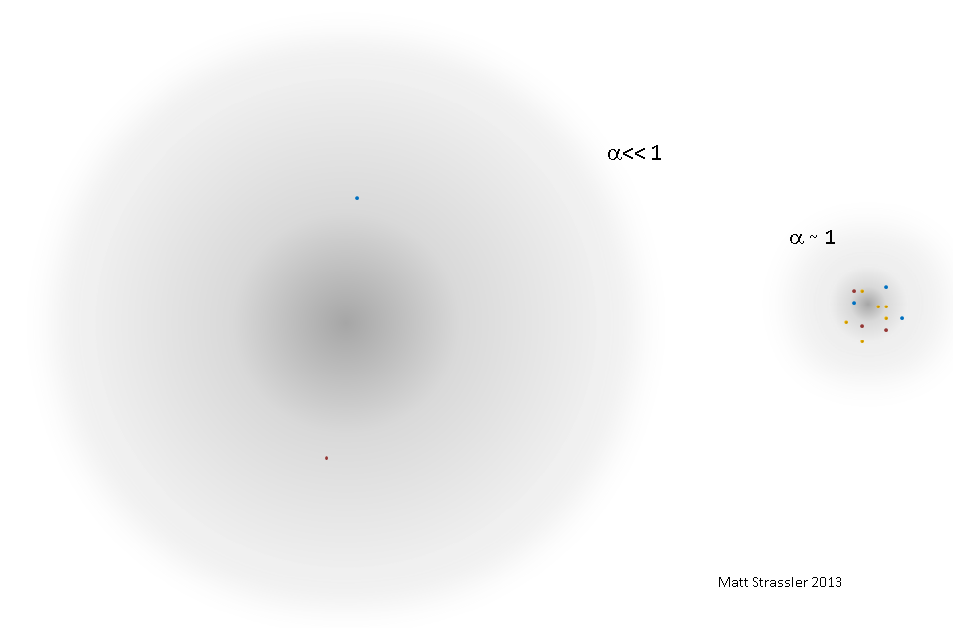
LargeSmallAlpha
Fig. 1: The simplicity of positronium (which closely resembles the simplicity of a hydrogen atom) would become considerable complexity were α close to 1. Electrons are drawn in blue, positrons in red, and photons in orange.  Were electric forces much stronger, positronium would be much smaller (not drawn to scale; it would shrink by a factor of 100 in radius), and its mass quite different from 2m.  The particles inside it would be faster, more energetic, more numerous, changing in number, and less easily identifiable as “real particles” (as opposed to the more general disturbances in fields called “virtual `particles’ “.)

As α increases, the force (at any given distance) between the electron and positron becomes stronger, and since the force pulls harder, it pulls the particles in the atom-like state tighter together. The particles move faster, approaching the speed of light. The motion-energy of each particle becomes larger; and the magnitude of the interaction-energy becomes larger, so the binding-energy becomes larger — becoming comparable to 2m itself. Conequently, the mass of the atom-like state is no longer approximately equal to 2 m. The size of the atom-like state becomes smaller, so that the time it takes light to cross the state, the time it takes the particles to move from one side of the state to the other, and the time between heartbeats of the particles all become about the same.

The stronger force between the electron and positron makes it more common for virtual photons to be present; and the larger amount of energy flying around the atom makes it easier for the virtual photon to itself become a virtual electron and positron. And in fact, when that happens, it can become difficult to say which electron is real and which is virtual, because there are also powerful forces between the two electrons, and between the electron and either positron, and these can cause a particle that was real to become one that is virtual, and make the virtual one real, and back again. Meanwhile, the virtual electrons and positrons can also release or absorb photons, which may be virtual but may sometimes be real.

In fact the very distinction between real and virtual particles starts to become difficult to decide.  Real particles are supposed to be well-behaved ripples in a quantum field. But with the atom-like-state so small, it really only takes a single heartbeat, more or less, for an electron or positron to cross this atom, at which point powerful forces will already cause it to change direction.  How can we say that such a particle is a “well-behaved ripple”? A well-behaved ripple should, well, ripple for quite a while — for many heartbeats — before being affected by external influences.  Here, our electron, while more like a real particle than the generic virtual particle, is still highly distorted, and doesn’t fit the definition of “real particle” anymore either. And the electron may not even be around for long.  The production of a virtual electron-positron pair can be followed by the annihilation of the formerly-real electron with the newly formed positron, leaving the maybe-virtual maybe-real electron behind.

So instead of what we had at small α — a simple system of mass just below 2m, consisting of an electron and a positron moving at speeds well below the speed of light — we find, as α approaches 1, an exceedingly complex system, with multiple particles moving at or near light-speed, with a mass that is very different from 2m.  (See Figure 1)  It’s impossible to say how many particles are inside; do you count the real ones only? and if so, how do you precisely distinguish the almost real ones from the mostly virtual ones? The number of real particles can be constantly changing.

Those of you who’ve read about the proton may note some similarity.  There are important differences too, but yes, the similarities are not accidental.

Now this is what is characteristic of a truly strong force; the objects that it forms are vastly more complex than atoms. Scientists were lucky, in a sense, that the first objects that were encountered on the road to the theory of quantum field theory were atoms. These are held together by a weak force — the electromagnetic force — and were easy to understand using the simpler mathematics of quantum mechanics, in which the number of particles is held fixed. Protons, by contrast, are held together by a strong force — the “strong nuclear force.”   So it’s not that surprising that protons are much, much more complex internally than atoms. (And I haven’t even attempted here to tell you about some of the additional complications that arise there; those are covered in this article.)  Inside a proton, the number of particles is continuously changing — which requires the much more complex mathematics of quantum field theory.

By the way, the electric force between two electrons is weak because α is small. The same is true for forces between any two elementary particles, because the all of the known particles have electric charges that lie between -e and e — for instance, top quarks have charge (2/3) e.  You might, however, wonder about the force between an electron and a uranium nucleus, since the uranium nucleus has charge 92 e. Well, in that case the force does get pretty strong! But this only has part of the effect that I’ve described for strong forces, because changing the charge on only one of the objects involved (and in particular the heavy one) doesn’t increase the probability for finding virtual electron-positron pairs. That would only change if the electron itself got a much larger charge than e!  So even a uranium atom remains rather simple compared to a proton…

How Weak is the Weak Nuclear Force? It’s Tricky…

How strong are the other known forces of nature? We’ve seen that electric forces have a strength α, at least at macroscopic and even atomic and subatomic distances. And over those distances, down to a millionth of a millionth of a meter, α is a constant; it doesn’t depend on r, which is part of why it’s such a convenient quantity.  But in fact, the strength of a force can change with distance, which complicates matters.  For electromagnetism, this isn’t so important; the effect is very small.  However, for other forces, it is a big deal.

The so-called weak nuclear force is, of course, weak. Well, it is weak at macroscopic, atomic, and even nuclear distances. But in fact its strength isn’t constant. For distances large compared with ℏ c/MW ~ 3 × 10-18 meters, i.e. (about 1/300 the radius of an proton), where MW = 80 GeV/c² is the mass of the W particle, its strength αweak is (roughly)

  • Fweak r² /ℏ c = αweak(r) = 0.02 e-Mwr/ℏc

The exponential e-Mwr/ℏc makes the force remarkably weak! Even at distances the size of a proton, this factor gives a suppression of e-300, which means the force has already decreased by a number so spectacular I can’t write it out here: it is a 1 with 130 zeroes after it. (That’s bigger than a `googol’, a 1 with 100 zeros after it.) And the force becomes rapidly weaker from there. Why? The same effect that gives the W particle (a ripple in the W field) a mass makes it impossible for a particle to distort the W field over long distances, in contrast to the effect of an electron or proton on the electric field. Consequently, the force generated by the W field is completely ineffectual at long distances.

But for even shorter distances,

  • αweak(r) = 0.02

Notice this is several times stronger than the electromagnetic force! The weak force is not intrinsically weak at all.  See Figure 2.  (Minor Caution: I’m leaving out a subtlety involving the interplay of the weak and electromagnetic forces at such short distances, and a very slow change in the force that becomes noticeable at vastly shorter distances.)

What makes the weak force so weak, when we observe it in the physics of nuclei, atoms, and daily life is the large mass of the W particle. If the W particle were massless, effects of the “weak” nuclear force would be stronger than those of the electric force! [This is another context in which the Higgs field, which gives the W its mass, is really important to our lives!]

The Strong Nuclear Force

The strong nuclear force, which pulls and pushes quarks and gluons (but not electrons), does something quite different. At the distances we were just discussing for the weak force — 3 × 10-18 meters — the strong nuclear force is quite a bit stronger than both the weak nuclear force and the electromagnetic force:

  • Fstrong r² /ℏ c= αstrong = 0.11 (at r ~ 3 × 10-18 meters)

That’s really not so strong; it’s about a tenth as strong as a really strong force, and only about ten times stronger than electromagnetism. In fact, although they differ enormously at macroscopic distances, the strong nuclear, weak nuclear, and electromagnetic forces differ in strength by only about a factor of 10 at distances shorter than about 3 × 10-18 meters. This is remarkable, and perhaps not accidental. It’s a small step from here to the notion of the “Grand Unification” of these three forces — the idea that at much shorter distances, all three forces end up with the same strength, and become part of a more universal force.

But at longer distances, the strong nuclear force gradually becomes (relatively!) stronger. [Again, remember what we mean by “weak” and “strong” here; the force is actually becoming weaker in absolute terms as r increases, but relative to, say, electromagnetic forces at the same distance r, it’s becoming stronger.]

  • αstrong = 0.3 (at r ~ 10-16 meters)

That’s quite strong indeed! And by the time r reaches 10-15 meters, the radius of a proton, αstrong is bigger than 1, and becomes impossible to define uniquely.

In short, the strong nuclear force, which is only moderately strong at distances far smaller than the radius of a proton, grows (in relative terms) at larger distances, and becomes a truly strong force at a distance of 10-15 meters. (This is shown in Figure 2.) It is this truly strong force that creates the proton and the neutron, and a weaker residual effect of this strong force that combines these objects into atomic nuclei.  Other important effects of this force becoming so strong are the conversion of high-energy quarks and gluons to jets (sprays of hadrons).

Why does the strong force become gradually stronger as r increases? That’s a story for another day, but essentially it is a very subtle effect due to disturbances (“virtual particles”) in the very gluon and quark fields that are affected by the strong force. Similar effects impact the weak and electromagnetic forces, but have much less dramatic effects on those two forces, which is why I haven’t mentioned them before.  (For instance, at the distance of 3 × 10-18 meters, the electromagnetic α is closer to 1/128 than its long-distance value of about 1/137.)

Given how strong the strong nuclear force is, why don’t we encounter it on a daily basis? It has to do with important details of how the strong force binds quarks and gluons and anti-quarks so tightly into protons and neutrons that we never observe them separately. This is in sharp contrast to how the weaker electromagnetic force allows electrons to escape from atoms rather easily, making the phenomena of static electricity (including lightning) and electric currents (including those in electrical wires) possible.

The Strength of Gravity

What about gravity? Well, for the particles we know about, gravity is amazingly weak. For two (stationary) particles of mass m, the force of gravity has a strength

  • αgravity = GN m2 / ℏ c

where GN is Newton’s gravitational constant. Compare this with the case of the electric force, where α = ke2 / ℏ c; the role of k and e in electric forces is played by GN and m. (Here I am using Newton’s formula for gravity, but as long as αgravity is small compared to 1, Einstein’s formula for gravity between two objects is essentially identical.)

Now we can rewrite this in terms of what is called the Planck mass Mpl = 1019 GeV/c2, or about the mass of 10 million million million protons, or of 20 thousand million million million electrons. (This is about the mass of a paper clip. [OOPS! Proofread Failure.  This is obviously wrong.  Speaking approximately, Mpl = 1019 GeV/c2 = the mass of 1019 protons = the mass of 1019 Hydrogen atoms = 0.00002 moles of Hydrogen = 0.02 milligrams = about a tenth of the weight of a typical grain of salt.  Thanks to reader Al Schwartz for pointing it out.]

  • αgravity = (m / Mpl )2

So for two protons, each of which has a mass of about 1 GeV/c2the gravitational force between them has a relative strength of the square of (1/10 million million million), or (10-19)

  • αgravity = (10-19)2 = 10-38

which is a 1 preceded by 37 zeroes and a decimal point! Meanwhile for two electrons

  • αgravity = (10-19)2 = 3 × 10-46

which, since an electron has a mass almost 2000 times smaller than a proton, corresponds to a force four million times weaker. Even for a pair of top quarks, nearly 200 times heavier than a proton and with the largest masses of any known particles, the gravitational force has a strength of only

  • αgravity = 10-34

That’s about 100,000,000,000,000,000,000,000,000,000,000 times smaller than the electric force between two top quarks.  That’s why gravity doesn’t show up in Figure 2.

If you think about it, this incredible weakness of gravity explains why you (using electric forces that power your muscles and keep your body intact) can move so freely despite being pulled on by the gravitational pull from the entire, enormous earth. In fact it even explains why the earth can be so much larger than a single atom; gravity wants to crush the earth, but the integrity of atoms, whose electrical forces resist this crushing, prevents this. If gravitational forces were much stronger, or electric forces much weaker, gravity would crush the earth down to a much smaller size and a much greater density.

Gravity is so weak that it’s amazing that we could discover it at all. So why was it the first force we humans knew about? The reason is that it is the only force that survives to very large distances in ordinary matter.

  • The weak nuclear force becomes extremely weak at long distances.  (We’ll see in a moment that the same is true of the Higgs force.)
  • Electromagnetism survives to larger distances, but though not very strong is still strong enough to bind up most electrons and atomic nuclei into electrically-neutral combinations, whose electric forces on other objects cancel. [For instance, a hydrogen atom does not have pull on a distant electron, because the electron in the hydrogen atom pushes and the proton in the hydrogen atom pulls that electron, with forces that essentially cancel.]
  • The strong nuclear force is so strong that it binds quarks and gluons and anti-quarks together into combinations that similarly have cancelling effects.
  • But gravity cannot be arranged to cancel in this way. There are no particles that generate gravitational forces that push things apart, so you can’t combine two particles so that their gravitational forces on all distant things cancel.

The Higgs Force!?

As of 2012, we have a new force to think about: the force between two particles induced by the Higgs field! This is not to be confused with the effect by which the Higgs field gives the known elementary particles their masses; the Higgs field can do this to a single, isolated particle. That’s not a force; it doesn’t push or pull.  But the Higgs field can also induce a force between two particles; this happens in much the same way that electromagnetic forces are created.  However, as far as its effect on ordinary matter, this force is very, very hard to detect.  At short distances, for particles like electrons and the up and down quarks that dominate the proton, the Higgs force is very weak (much weaker than electromagnetism, but much much stronger than gravity).  At long distances, like the weak nuclear force, the Higgs force becomes extremely weak, because the Higgs particle, like the W particle, has a mass.

The Higgs field induces a force similar to the weak nuclear force in that it has a very short range, becoming ineffectual at distances long compared to ℏ c / Mh ~ 2 × 10-18 meters (1/500 of a proton’s radius), where Mh ≈ 125 GeV/c² is the Higgs particle’s mass. And at first glance the formula is similar to that of gravity, in that it is an attractive force proportional to the masses m of the two elementary particles being attracted.

  • αHiggs = (mc2 /4 π v)2  × e-Mhr/ℏc  (for r »  2 × 10-18 meters)
  • αHiggs = (mc2 /4 π v)2                      (for r «  2 × 10-18 meters)

where v = 246 GeV is the constant value of the Higgs field found throughout the universe. [Actually, if one is careful, there is an extra square root of 2 in there, but let’s keep the formulas simple-looking.]

Be cautious!  The resemblance to gravity is misleading. This formula is only precise for the known elementary particles — those objects that get their mass from the Higgs field. It works for electrons and muons and quarks.  It is not correct for protons, neutrons, atoms, or you! That’s because a proton’s mass (and a neutrons, and therefore an atom’s, and therefore yours) does not entirely come from the Higgs field. This is in contrast to the formula for gravity, which is correct for all slow objects! Instead, for ordinary atomic matter, we’d have to replace the formula with one that looks similar but has a different factor in front, slightly different for each atom. Qualitatively, however, the dependence on the distance would remain similar.

Also, the formula I’ve written also assumes there is only one Higgs field and one Higgs particle (which we don’t yet know to be true, but is the simplest possibility consistent with current data.) If that’s not the case the formula will become more complicated, while remaining of a similar form.

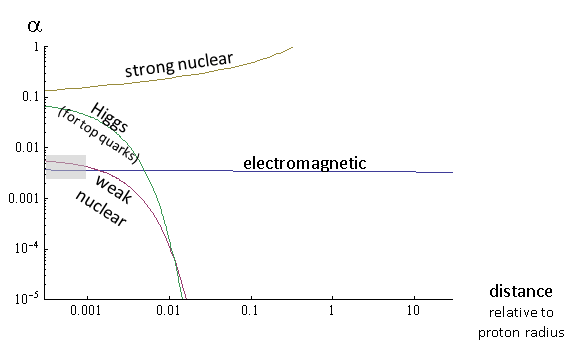
Fig. 2: The relative strengths (α) for each force, as a function of radius, between about 1/300 of a proton's radius and 30 proton radii.
Fig. 2: The relative strengths (α) for the forces acting on a top quark and top anti-quark, with mass almost 200 times larger than a proton, as a function of radius, between about 1/3000 of a proton’s radius and 30 proton radii.  The Higgs force and the weak nuclear force become extremely weak at distances even smaller than the proton radius, while the strong nuclear force becomes strong at the proton radius. Electromagnetism stays moderately weak at all distances.  There are subtleties, ignored here, involving electromagnetism and the weak nuclear force at sufficiently short distances (grey box). Gravity is incredibly weak and lies far below this graph.  For the up and down quarks in the proton and neutron, the graph would be similar, except that the Higgs force would be far too small to appear on the plot; the same would be true for two electrons, though it is unaffected by the strong nuclear force.

How strong is this force? Well, at very short distances, shorter than 2 × 10-18 meters, the Higgs force between two top quarks is comparable to the strong nuclear force at that distance (see Figure 2)! But for electrons, which have a low mass because their interaction with the Higgs field is small, the force even at  short distances would be much weaker than electric forces — more than a thousand million times weaker — though still thousands of millions of millions of times stronger than gravitational forces between electrons. Yet if you consider two electrons in an atom, which are about ten million or so times further apart than 2 × 10-18 meters, then the Higgs force between them is much, much smaller even than the tiny gravitational force between them, as it is suppressed by e-10,000,000. [Even if the Higgs field did give protons and neutrons all their masses, the Higgs forces inside a nucleus would still be vastly smaller than those of gravity, which in turn are incredibly small compared to the residual strong nuclear force that holds the nuclei together.]

It is the incredible weakness of the Higgs force in the context of ordinary matter that makes it so hard to discover. On the one hand, the Higgs force, like gravity, is always attractive and can’t be cancelled.  But on the other hand, that’s irrelevant, because, like the weak nuclear force, the Higgs force does not survive to long distance, because the Higgs particle, like the W particle, has a mass. The Higgs force at ultra-short distances is much stronger than gravity, but at nuclear and atomic distances, it is much weaker, because of the Higgs particle’s mass. And for the low-mass particles out of which we’re made, which interact weakly with the Higgs field, the Higgs force is always thousands of millions of times weaker than electric forces, even at very short distances.  So even though every atom in the Earth exerts a Higgs force on every other atom in the Earth, that force is so incredibly minuscule, even for neighboring atoms, and especially for distant ones, that it has no detectable effect.  This is why we had to go find the Higgs particle directly to confirm the Higgs field exists; we couldn’t just go looking for the force it creates, the way we can use the observation of electric and magnetic forces to confirm that the world has electric and magnetic fields.

When might we actually observe this new force? It’s effects will first be observed either in the scattering of W and Z particles off each other (which will eventually be done, indirectly, within the proton-proton collisions at the Large Hadron Collider) or in the interaction between a top quark and a top anti-quark (which can be observed at an electron-positron collider — in fact I wrote my first particle physics paper [see in particular Figure 11 of the paper] about this very phenomenon.)

113 Responses

  2. Pingback: CALCULATORS ON-LINE CENTER SUBJECT: F-P - Martindale Center
  3. Pingback: Rumus Gaya dalam Fisika Beserta Pengertian, Macam-macamnya dan 3 Contoh Soal - Science | Kabarwarga.com
  4. Pingback: CMS catches the top quark running – ParticleBites
  5. Pingback: The final TOE (Theory of Everything) | The Great Vindications
  6. Pingback: อะไร คือ แรงนิวเคลียร์อย่างเข้ม? | ครูฟิสิกส์ไทย

  7. I like this article. It triggered my imagination about Grand Unification in a right way. Thanks to the author

    Reply
  8. Pingback: Attractive higgs force and inflation | Question and Answer

  9. I found this article looking for a comparions between gravitational and electromechnical forces and found it fascinating reading. Would you have a book you could recommend that I could read more of your writings?

    Reply
  10. Pingback: Quantum Field Theory, String Theory and Predictions (Part 8) | Of Particular Significance

  11. Even though the weak and strong interactions vary greatly over very small distances, is there a fundamental source strength term analogous to the source terms for E&M and gravity that one could use for the definitions of the “alphas” for these interactions that could be separated out from their small distance varibility?

    Reply

    1. The electromagnetic fine structure constant is a very well-known fundamental value published in lots of places. Here, for instance: http://physics.nist.gov/cgi-bin/cuu/Value?alph|search_for=abbr_in!

      The strong force version is a function of radius not a simple constant, and so it’s not documented as widely. Do particle physicists have a standard handbook of these things, or is it a question of tracking down the right textbook?

      Reply

        1. Hi Matt. I think there is a type error. Shouldn’t the formula for the heartbeat time of a wavicle be h/mcsquared not hc/m?

          Reply
  13. Pingback: Quantum Field Theory, String Theory and Predictions (Part 4) | Of Particular Significance
  14. Pingback: Quantum Field Theory, String Theory and Predictions (Part 3) | Of Particular Significance
  15. Pingback: Key mission of life | The Great Vindications
  17. Pingback: Final Day of SEARCH 2013 | Of Particular Significance

  18. F r² = 0.007 ℏ c = ke^2 -> I got “approximately 0.007(297… etc.)”(=ratio of (Fr^2)/(ℏ c ), =unitless) by setting “e” as the value of elementary charge (=1.60217657… × 10-19 coulombs) but if the amount of “an elementary charge” is not used for “e”, (Fr^2)/(ℏ c ) is not 0.007(=the coupling constant). To get “a fixed value(=constant value)” of “Fr^2″=”ke^2=(*1)” or (Fr^2)/(ℏ c )=(a coupling constant), you need to have a fixed chunk(unit) of “a charge(of e, m, color charge etc.)” Is this not the case? It seems that to compare any two fundamental forces by the values given by “Fr²”, or “(Fr^2)/(ℏ c )” you need to have some kind of a “chunk(quantum)” in “charge(e, m, color etc.)” given by nature or you just have to use the “m” value and the “e” value for existing/observed (elementary) particles. So, the value of the coupling constant 0.007.. is calculated for two point-like particles with “an elementary charge” for each? but any other two (point-like, elementary) particles with greater or less “electric charge” than “an elementary charge” has a coupling constant (for electric charge) of other values? For example, two “quarks” can have either -1/3 or +2/3 electric charge, (−2/3 or +1/3 for anti-quarks), a coupling constant (for e charge) for two quarks must be different from 0.007..? And what about a charged object/system that acts like a (point-like?) particle such as a charged black hole? If two charged black holes (with different amount of multiples of elementary charge) can act like a point-like particles, they should have yet another a coupling constant (for electric charge/force)?

    btw,
    unlike Fr² or ke^2 or (Fr^2)/(ℏ c ), Coulomb’s constant(k) or Gravitational constant(G) seem to stay constant regardless of charge amount (“e” or “m”) or r(=distance) numerically(=meaning if considered only within these equations.) but because they have different units, it seems impossible to compare k and G. (does not make sense..? or? there is more to them if considered beyond these equations that take the form of F=k(“charge”^2)/(r^2)? or what?)

    1)=this value seems to stay more or less constant regardless of r if “shielding effect”(or the effect of virtual particle pair production at very close distance etc.) is ignored. I have to check/calculate how exactly “shielding effect” etc. affects the force strength or coupling constant though.. (and I am not sure how to do this precisely.)

    Reply

    1. As you notice that e is NOT the smallest (and thus elementary) charge; down type quarks have 1/3 this charge and up type quarks 2/3 of it. There’s no reason at all that some exotic physics might throw up a particle with a tenth of this charge or any amount of it at all. The electron’s charge is a useful unit but there’s nothing ‘special’ about it.

      When we calculate α the first step is to multiply k * e * e. What we are doing is setting ‘e’ as 1 in a sense so that 1 x 1 = 1 and it (charge) can be ignored. Now k has units of Nm^2/C^2 and it’s the C^2 that’s important. e appears in it in that 1 C = 6.241 × 10^18 e.

      Imagine now that we are going to use 2e as out ‘1’ If we just plug in 2 into the equation we will get an ‘α’ that is four times larger. But we didn’t set 2e as 1! our answer is in fact 4α. In order to set 2e as 1 we must also alter k since k had 1e in it hidden away. To do this the ‘C’ becomes half as large (since there is half as man 2e in 1C as there is e’s.) Since k has units of /C^2 it becomes four times smaller. 1/4 * 4 = 1 and α remains the same!

      The same is true of all our αs for various forces, their k has in it somewhere *the same unit we are setting as ‘1’* when working out α. The very fact that α must be independent of charge (It cannot even be considered ‘per charge’) means you have to pay attention not just to the units of e (or m, etc) but also those of k. k, G, etc are constant ONLY when considered as ‘per’ [PER Coulomb, PER kilo].)

      α is unitless and to make it so you must carefully cancel between the units of your charge and the units of k (Or G, etc.)

      Reply

  19. “we are simply talking of the properties of any given elementary particle. We can consider an electron or a proton as examples.” -> ok, so this means, just compare the forces btw an electron and a proton (or electron and positron or any combination of two particles) for example, and calculate the force by “e” and the force by “m” and compare the strength of the two? Is that all this article is talking about? is that simple (that is all?)? but, then, this means a coupling constant does not have a single value (assuming the r(distance) is fixed)? because a coupling constant depends on the amount of charge like “e” and “m.” I do not see where/how the each alpha=each coupling constant is coming from(calculated) except “electric charge.” in this article.

    Reply

    1. Some very good points. You have made me realize that your question is more complex than it seemed and that a lot of my previous post was in error and focused on the wrong ideas. Disregard it. (If you see this professor please delete my previous comment.) Starting afresh:

      The first thing to note is that ‘charge’ is simply a measure of how a field changes around a certain point. The electric charge of an electron causes the electromagnetic field’s value at various points from that charge to change in a predictable manner. In itself this doesn’t mean much.

      A force arises because there is an energy involved in this change of a field. When talking about strength in the ‘usual’ manner this depends both on the rate of change of the field per distance unit. That depends on both the ‘charges’ involved and the number of distance units they are separated by. For the electromagnetic force this is ke^2/r

      What is being spoken of here however is a strength independent of distance and charge. To find this we must remove both of those things. Charge can be removed by setting e (Or m, etc) in ke^2 to the same value of charge used to calculate k (Or G, etc.) This makes k and e related, changing the value of e used to calculate k changes k. ke^2 thus becomes independent of ‘charge’ for the force.

      By removing r and instead dividing by ℏc we remove the dependence on distance and instead relate the force to a fundamental limit of the universe, the speed of light. More importantly it relates the energies of the force to the energies at which a number of effects (such as the creation and particle-antiparticle pairs) become important.

      A weak force is one that it is very difficult to create a system where these effects are important while a strong force is one where such systems form easily. Under this arrangement and definition the magnitude of the ‘charges’ involved are just a variable that can be changed. Electromagnetism is weak because it is very difficult indeed to create system where things like particle-antiparticle pairs are important. (It could in theory be done with very high charges and/or short distances, but it’s not easy.) The strong force is strong because it is very easy indeed to create such a system, all protons are one.

      There is probably a better and more accurate way to word this; your question made me realize I still do not entirely understand everything laid out here. I hope this helps though.

      Reply

  20. At small enough scales you reach a point where you can no longer meaningfully measure something, be it mass or energy, time or even space. This gives us a certain limit to the smallest mass, etc. (While not ‘clean’ like the fundamental unit of electric charge there exists a certain amount of mass which, if two masses differ by less than it, we cannot measure that difference in any meaningful way.)

    But even if gravitational ‘charge’ were quantized how would we know that one gravitational charge ‘equaled’ one electromagnetic one? It is like comparing apples and oranges.

    However in this case the situation is more prosaic; we are simply talking of the properties of any given elementary particle. We can consider an electron or a proton as examples. There is some variation in say mass-to-charge ratios but not significant enough to affect our arguments here. In fact no elementary particle exists that would substantially alter the arguments given here. It is possible to imagine a system (such as two charged black holes orbiting each other.) where say the electric force begins to act differently but this is little more than a side note to the arguments presented here.

    Reply

  21. How can you compare the force strengths with “which amount of charge”? For “electric charge” the amount of elementary charge could be used for a typical(the smallest)? amount of charge that an elementary particle(like an electron/positron etc.) possess but what about gravity? and other forces(weak & strong)? “mass(=m)” in gravity in (F=Gm^2 /r^2) looks like “e” in (F = ke2 / r^2) but m is not quantized(?) nor does it have the smallest quantum(chunk)(?) Then, how can you compare the two? if “m” does not come in a “chunk(quantum)/ or the smallest unit”, it seems impossible to compare the two forces. Or all the charges (electric charge, color charge, and mass etc) are quantized and comes in the smallest indivisible chunk/unit? Electric charge seems to have the smallest amount/unit (an elementary charge or 1/3 of it for a quark?) but “mass” has the smallest unit/quantum? What is the evidence? Or, they(physicists) just assume that it comes in the smallest unit like the Planck mass, and calculate the relative strength of force created by “e” and “m”? but the Planck mass is not the smallest possible mass unit/quantum/chunk? So, why on earth the Planck mass appears in this article? And, are “charges” for weak and strong force also come in the smallest chunk like “the elementary (electric) charge”?

    Reply

  22. Prof. Strassler, I apologize – you answered my question quite nicely in your “virtual particles” post. Thanks a bunch. You have cleared up a mystery that has afflicted me for many years!

    Reply

  23. Prof. Strassler, I hope I’m not too late to ask a question on this thread (I just discovered your blog and I am thrilled that you are trying hard to convey these subtle concepts to the public). My question: I’ve always had trouble making sense of the metaphor that forces result from the exchange of virtual particles. There is an asymmetry here: forces can be attractive or repulsive, but the “exchange” metaphor does not seem to accommodate this asymmetry. Other commenters have asked this question, in somewhat different words, but you punted. I’m hoping you can give us some intuitive understanding without feeling you have to write a whole article.

    Reply

  24. α = ke2/ ℏ c = 0.007 297 352 57. So, ke^2 = mass? – Here, mass of a partice also defined by charge.
    Because α is one of the most precisely measured quantities in nature, the perturbative nature of eigenstates energy level differences in atom create a parallax of apeiron and perion (quantas)- thus give mathematical authenticity? So the calculation of angular momentum was possible using pythagorean axiom.
    Because particles travel slower than light the Relativistic quantum mechanics was also consistent.

    This discreteness become not doable, when α reaching closer to 1. Eventhough mathematics of relativity can solve the problems of particles reaching the speed of light, the shrinking 1/α² heartbeats, will again make parallax between virtual particles and real particles – thus making mathematics of Algebraic geometry possible – even at the absence of apeiron and perion and axiom – duplicating consciousness ?
    The amplitude that a virtual particle exists interferes with the amplitude for its non-existence, whereas for an actual particle the cases of existence and non-existence cease to be coherent with each other and do not interfere any more. So Virtual particles are excitations of the underlying fields, but also duplicate measurable particles. Thus making numerical production of concrete geometry of space possible – like hologram or quantum 3D print ?

    Reply

  25. Hi, great article! Possible typo: shouldn’t the interaction energy of positronium be -mc² × α²/4 rather than -mc² × α²/2 ? (-2 x E.K.). On a related note, shouldn’t the binding energy be negative too?

    Reply

    1. The total kinetic energy is that of the electron AND that of the positron, so that explains the factor of 2. For hydrogen, all the kinetic energy is essentially that of just the electron.

      The sign of the binding energy (B) is a matter of convention. I choose to state it as a positive quantity, but that just means that the mass of the state is 2 m_e – B, not + B.

      Reply

    1. I’m afraid (for reasons I can’t determine from your comment) that you’ve fully misunderstood what you’ve read. You said “If the source of the energy is turned off then the wave structure disappear.” That’s entirely false. You also wrote “The wave structures in a box requires a box.” That is true, but has nothing to do with a source of energy. The box neither adds nor removes any energy. So unfortunately your statement “A continuous energy input is required to maintain the wave structures” is completely wrong; NO energy input is required.

      In the same way, no energy input is required to maintain the proton once it is created. Indeed, the world would not have any protons in it, were continuous energy input required. Protons are not like engines; they do not take energy in and send exhaust back out. Once created, they will stay as they are, unless they are hit hard by something else.

      So I encourage you to go back and figure out how you misunderstood what you read in Wikipedia. Of course it is possible that wikipedia has an error on this point, but more likely you misunderstood it.

      Reply

      1. This article, “The Strengths of the Known Forces”, I hope has resulted in achieving your objective.
        Almost every comment has a version of
        “I have a question”
        and
        “Thank You”
        Put me on that list for encouraging me to continue searching for knowledge.
        Your answer,

        “In the same way, no energy input is required to maintain the proton once it is created. Indeed, the world would not have any protons in it, were continuous energy input required. Protons are not like engines; they do not take energy in and send exhaust back out.
        Once created, they will stay as they are, unless they are hit hard by something else.”

        That is why I’m still trying to get an understanding/explanation for the proton.

        Reply
  27. Pingback: Courses, Forces, and (w)Einstein | Of Particular Significance

  29. Unanswered questions.

    1. Where does the energy come from to create the disturbance in space that result in a sphere of strong force, (proton)?

    Why does this sphere of energy appear to be permanent/stable. It does not appear to need a continuous input of energy to maintain itself. It does not appear to be “leaking any energy”.

    Does the existence of a proton violate Conservation of energy? It does appear to be a perpetual machine.

    Reply

    1. 1.) Like most of the particles that make up the universe protons were manufactured in the Big Bang, a hot, dense high-energy state. While not as simple as just pulling protons from nothing it’s a quite intuitive explanation. If you want to ask where the energy of the Big Bang came from things get more complicated. (And head towards ‘Why is there something instead of nothing?’)

      2.) The proton is stable in the same way a pile of ashes isn’t flammable. Anything and everything that exists has energy (Including mass as energy.) Roughly, things will only decay if they can break down into products that contain ‘less energy’*. (A neutron decays quickly into a proton, electron and anti-neutrino. In fact nearly all known particles decay in the blink of an eye.) The proton has energy, yes, but it cannot have or break up into anything that has LESS energy. It is the ashes of a fire that has burned out, a car without gas.

      * ‘less energy’ is not accurate but a nice way of thinking about things.

      3.) To violate the conservation of energy a machine of any kind must either destroy or make energy from nothing. ‘Perpetual motion machines’ are not impossible, an atom will have all its parts moving for an indefinite amount of time. What IS impossible is a machine that gives you more energy out then you put in. As protons are the lowest energy state they can be, as they cannot ‘leak energy’ there is no way to make them produce energy from nothing.

      Reply

  30. Professor, an excellent and informative article as always, with awesome neatness.

    If strong nuclear force is really separated (splitted) will release incredible strength – more than residual strong nuclear force ? (because in long distance it become more than 1 – fig 2).
    We can interpret this, “there is already a Grand unification at very short distance much, much lesser than 2x 10^-18 meters?” – there is already high energy there ?

    The Higgs force was the force of Grand unification, which encapsulated, the quanta or quantum of action ?
    This “quanta” breaks the continuity (apeiron) at nuclear distances – like the appearance of neutron and proton.
    Then, Phenomenologically we say, this “quanta (mathematical)” as mass ?

    The high energies created in LHC, will only break the Asymmetries and release the force ?

    Reply

    1. The amount of energy you can get out of a system is not simply related to the strength of the force that holds it together. It’s much more complex than that. So the answer to your first question is no; it turns out you can’t split protons or neutrons. Long story.

      There’s no energy in a force, per se. If I have two objects held together at very short distance, the energies involved in keeping them there will be very large. That’s partly just because the distances are short, not just because the forces are “strong” or “weak” in the physicists sense. Meanwhile, this does not mean I can obtain large amounts of energy from such a source. I may have to put *in* lots of energy, rather than drawing *out* lots of energy, in order get these objects to stay together, or to pull them apart.

      The Higgs force has nothing to do with grand unifaction; it isn’t part of the unification force, and it doesn’t have any role in Grand Unification. In old-style grand unification, there is another, Higgs-like field which plays a role, but it isn’t the Higgs field that we’re talking about at the LHC. And there may be no such field in newer versions of unification.

      Energy, at the LHC or elsewhere, cannot “release a force”. And the LHC cannot probe grand unification anyway; that would require a machine with collisions a million million times more powerful.

      Reply

      1. Thank you Professor,
        it will take lifetime to get intuitively, the meanings of mass, force and energy.

        Reply

  31. Dear Prof. Strassler,

    Many thanks for another excellent article! I have a question that may tie in with the weak vs. strong force distinction: It is about the concepts of “elementary” and “composite” particles.

    After getting a glimpse of QFT I find this distinction confusing. My understanding is: The state that we call a physical electron is a kind of resonance that involves both the (bare) electron field and the photon field (in the full SM we even need right- and left-handed electron fields, the Higgs field and others). Although it can be treated perturbatively due to the EM force being “weak”, the physical electron is not even “close” to a bare electron quantum, as renormalization tells us that we have to ascribe absurd infinite properties to the latter to end up with a realistic physical electron.

    The state that we call a proton is a kind of resonance that involves the quark and gluon fields (and others). Due to the strong force being “strong”, we cannot describe a proton using perturbation theory.

    As neither the electron nor the proton can be explained using a single field, what distinguishes one of them as elementary and the other as composite? Is there any fundamental difference that I am missing? Or is it that the quantitative difference (i.e. weak vs. strong) is just so large that it makes sense to use different terminology for the electron and the proton?

    best regards

    Edwin

    Reply

    1. This is an excellent and very deep question. It’s the kind of question that I would discuss extensively with graduate students, and I am reluctant to answer it here precisely because requires a deep, technical discussion — beyond the scope of this website.

      What is the current status of your training? Are you a beginning graduate student?

      Reply

      1. Dear Prof. Strassler,

        I wish I could say “yes”, but the status of my training is a bit complicated. Many years ago I studied physics for two years, then I switched and made my master in computer science. However, my love for physics and mathematics has never died and I’ve been wrestling with Peskin & Schroeder, etc. on and off in my spare time. Having found that I lack too many of the fundamentals, I’m now working through more humble texts like Dirac’s Principles of QM and I have taken up studying mathematics. Alas, progress is slow next to my full-time job.

        Your website is very valuable to me, as it fills in many insights and intuitive explanations that are so hard to come by in text books. There is such a gigantic stretch nowadays between the popular expositions and the “real thing”, so any intermediate level of information is precious, especially for someone like me who has no access to the “oral history” passed on at universities.

        best regards

        Edwin

        Reply

        1. Here’s the simplest way to answer, then.

          The most obvious sign that an object is composite is that you can excite it internally. Of course atoms can be excited. You can make an excited version of the proton; the lowest-mass excited proton is called the Delta. And then there is a large tower of additional, more massive states. The mass scale for these excitations is a few hundred MeV. And indeed, the size of the proton is hc/few hundred MeV, or 10^(-15) meters. The reason the size and the excitation energy are similar (which is not true for atoms) is that the force that binds the system together is a strong one. If the force is weaker, the excitation energy is smaller than the corresponding inverse size.

          There is no excited version of the electron with mass below 1 TeV. [The muon and tau are not excited electrons; if they were, they would rapidly decay as muon –> electron + photon, whereas in fact this decay never happens.] This tells us that the electron is smaller than 10^(-18) meters.

          So even though an interacting particle is a complex object, there is still a notion of size which affects whether there are excited versions of that particle. Yes, an electron has, as part of its very nature, a “cloud” of photons and electron-positron pairs around it; but that cloud has no independent existence, and you can’t excite the cloud into a higher state. That’s different from the “cloud” of electrons around a nucleus inside an atom, and its different from the “cloud” that is a proton.

          Reply

          1. Thank you for your answer. It naturally raises the question: When do we interpret two states as different states “of the same object” (which is not a directly observable relation, to my understanding)? I guess part of the answer is: If only the spacetime-related eigenvalues differ between the states. Maybe there is also a pragmatic part: When it makes obvious sense to organize the states like that. – But then this might head towards the discussion you do not want to enter here.

            Anyhow, the difference you point out between the electron’s “cloud” and the “cloud” around the nucleus is an interesting example and I think it will make a good test of my understanding if I try to state this difference in precise terms for myself (as soon as I’m up to that).

            Reply

            1. To some extent, interpreting two states of nature as different states of the same object has to do with how we think about that object’s properties. Why do we view the ground state of Hydrogen and its first excited state as the same object in two different states? Because the excited states readily decay to the ground state emitting nothing but a photon, which is a particle that we know is associated with the same force that holds Hydrogen together. A similar statement applies for the Delta, which decays back to a proton by emitting a pion. But a muon decays to a neutrino, an antineutrino and an electron, via a short-range force that we know isn’t holding the electron together.

              But I have a feeling there’s a better answer, and maybe I can come up with it, if I think harder about it.

              Reply

          2. Apologies for the following: replying at the wrong conversation level, replying to a year-old thread, digging at something that you probably can’t/don’t want to answer without equations.

            Concerning the question further down about a muon being an excited form of an electron: could a particle (specific concurrent ripples in many fields) be excited in more that one of the fields that it interacts with? Could the muon be an electron that carries an excited waveform in another field that the electron normally interacts with, instead of the electromagnetic field? Specifically, could the muon be an excitation in the weak field? Note that the other particles involved in the decay – neutrinos – interact with the weak force, and that the ‘weak field’ is related to EM field locally.

            Thank you so much for being so involved with comments and such a fountain of knowledge.

            Reply

  32. Matt: “… the (still unobserved but surely present) Higgs force.”

    This is a highly speculative issue. Yet, it can be discussed conceptually, with two stories as below.

    Story one:
    Mother: Hi, baby, it is the time to hit the sack.

    Baby: I am still working on my homework, the neutron decay. How can a three string particle (u, d, d) become 5 strings (u, u, d, e, anti-e-neutrino), especially a “d” had a sex-change for becoming a “u”?

    Mother: This is the most famous fairy tale. Here comes an angel who gave the “d” a kick on its butt, and it comes the “u”.

    Baby: Who is the angel?

    Mother: Who? Who? The “W”.

    Baby: Then, where are this e and the neutrino coming from?

    Mother: Oh. The “W” angel flies away as the e and the neutrino.

    Baby: Where was the “W” angel coming from?

    Mother: There is a Higgs “field” which is omnipresent, and it has Higgs egg everywhere. The “W” angel was hiding in the Higgs egg all this time.

    Baby: Thanks Mon. This is a great fairy tale. I now can sleep in peace.

    Story two:
    Brother: Mon, your fairy tale is very interesting. But, I learned a different story about the neutron decay.

    Mother: There cannot be any different story. This fairy tale is the “Standard Model”. But, go ahead tell me your story.

    Brother: The (u, d1, d2) picks up a virtue d-pair (d3, -d3), the vacuum disturbance. And it forms a 5-quark blob. Then,
    Step 1: (d1, -d3) got together

    Step 2: (d1, -d3) turns into (u1, -u3), this is a vacuum state transforms into another vacuum state.

    Step 3: (-d3, -u3) got together. Then, this blob has a genetic exchange and flies away as the e and the neutrino.

    So, (u, d1, d2) decay into as (u, u1, d2, e, neutrino).

    Mon, you have mistaken this vacuum transformation blob as the Higgs egg.

    Mother: Your story follows all physics laws, and it makes sense. But it is wrong because that it is not the Standard Model. Only authority can be right. Higgs force has ensured that you are wrong.

    Reply

    1. Note: there was a typo, (-d3, -u3) should be (d3, -u3).

      This Higgs force speculation can go one step deeper, again, with a conversation.

      Baby: I don’t like your “vacuum blob” story. It is too rational and too cold. I like the fairy tale, not because of its being the Standard Model but because that it is “Magical”. A Higgs chicken (field) is omnipresent and can lay Higgs egg any time at any place at its choosing. Then, out it pops a “W”-angel when neutron got out of from bondage. Furthermore, no gadget thus far (including the LHC) in this world is able to distinguish your “vacuum blob” from the Higgs egg. That is, that fairy egg can be as real as the “vacuum blob” reality, and there is no gadget data can prove it otherwise.

      Brother: Hi, baby, for the gadget testing concern, you might be right for the next decade or two. But, in sports, any tie can be easily broken by “overtime”, the tie-break-litmus test.

      The Standard Model is absolutely correct in terms of that entire gadget testing data. But, as soon as it goes out of its baby crib, SM fails from left to right, from top to bottom. It (SM) cannot derive most of the “parameters” it used in the model (such as, the Cabibbo and Weinberg angles, the Alpha, etc.). Furthermore, it fails on all the following known physics facts;

      i. Planck data — dark energy (accelerating expansion of this universe), dark matter, Neff = 3 (minimum), etc. .

      ii. Neutrino oscillations

      iii. Proton’s stability

      iv. Guidelines for SUSY (with s-particle)

      v. About gravity

      vi. Unification between quantum and determinism.

      That is, the Standard Model is only the hodgepodge of the gadget data. And, simply it has “no” theoretical “base” for deriving those parameters and for connecting to those other physics facts.

      Thus, those other facts above become the overtime litmus tests. Anyone who can solve any one of those other facts or derive those free parameters is the winner of this contest.

      Baby: Yet, most of those issues are controversial and cannot be decided with the current gadget testing.

      Brother: Indeed. But, the Cabibbo – Weinberg angles and the Alpha are only three “numbers”. The only gadgets needed for testing them are “paper and pencil” which are in the hands of every first grader. There will be absolutely no controversy about whether an equation for calculating one of them is correct or not. Thus, we can simply choose Alpha as this overtime Litmus test, to be the “first” criterion for the correct final physics.

      Baby: That is great. But, verifying the “prediction” of a theory was the only criterion for physics theory thus far. How can you convince physicists to accept your overtime idea?

      Brother: Most of theory is the “extension” of known physics. Thus, it must “predict” something new in order to be credible. But, when a “system” is constructed from a “base” which contains no “known” physics of any kind, it is credible only if it can “reproduce” all known physics, not just any puny “prediction”. That is, system has “outcomes (or consequences)” while theory has “prediction”. And, there is a super strong requirement for “base”. It must not contain any “known physics”, that is, no known physics is “put-in” into the base. Thus, “reproduce all known physics from a base (without containing any known physics)” is the second “Overtime test”, the second criterion.

      Baby: Must a base be verified by gadget testing?

      Brother: No, no, and no! The “base” needs no verification. If a “wrong” base produces a system which can reproduce all known physics, it is a “good” base.

      Baby: Just heard in the news that a “W”-einstein had discovered the final physics theory. Do you know anything about it?

      Brother: No, never heard about it. If he can pass two tests,
      a. Litmus test — deriving the Alpha with a physics equation
      b. A base is able to reproduce, at least, the known 48 elementary particles
      then, he could be on the path to the final physics. Otherwise, even the “Z”-einstein won’t do any good.

      Baby: Obviously, the Higgs story failed the first overtime litmus test. Are you saying that the Higgs game is over? Is there Higgs force?

      Brother: Higgs force is “not” needed in the “vacuum blob” story which did pass the first litmus test, and its calculation is available at another blog (http://blog.vixra.org/2013/05/16/why-i-still-like-string-theory/ ).

      Reply

  33. This is great! It’s terrific to have articles that are one step in detail above the usual popular ones, without being actually mathematical.

    I think there might be a typo: “If α is large, then the time it takes light to cross the atom-like state is much larger, by 1/α, than the heartbeat of the particles that it contains.” Should be “If α is small”?

    Reply

  34. For gravity as a FORCE with graviton as force carrier , does this represent exclusive alternative to gravity as geometry ?

    Reply

    1. At present they are both two equal interpretations, like the various ways of looking at quantum mechanics. Neither one can currently claim to be ‘correct’ and the tension between relativity and quantum mechanics is interesting indeed. Quantum gravity often tries to reconcile the two.

      Reply

    2. No, these are complementary — two ways of viewing the same thing. The fact that gravitational fields can be viewed as geometry (even before we worry about gravitons or gravitational forces) is the meat of Einstein’s theory — but it doesn’t change the relation between fields, forces and particles when those forces are relatively weak. You have to be more careful when you start dealing with complicated gravitational objects like black holes or the universe as a whole.

      Reply

  35. I am still quite unsatisfied with the curve of the strong force , any curve representing a function cannot just stop nowhere , either it go to infinity in value /distance or it diminish to zero , would you please clarify this point.

    Reply

    1. Curves can and do stop, especially when what they are measuring breaks down. A classic example of this is in the phase diagram of water where at the ‘critical point’ the difference between liquid and gaseous water ‘vanishes’ http://serc.carleton.edu/images/research_education/equilibria/h2o_phase_diagram_-_color.v2.jpg In the case of the strong force, when the value starts to exceed 1 its definition breaks down. You can’t say a curve goes to infinity if you can’t measure or define it.

      It is a simple diagram, it even lacks gravity. Some detail has been sacrificed for clarity.

      Reply

    2. The reason I wrote this article now is that I have to go back to the protons and neutrons article, http://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-structure-of-matter/protons-and-neutrons/, and start to explain this question. It does not have a short answer. The relevant buzzword is “quark confinement”, though that’s not very meaningful by itself. What it means is that you can’t ever pull quarks or gluons far enough apart to give meaning to alpha_strong, but this is not because the force is infinitely strong. There are hints of how this works in this article: http://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-known-apparently-elementary-particles/jets-the-manifestation-of-quarks-and-gluons/

      Reply

  36. Matt, I’m looking for the fundamental difference between the electric and magnetic force:

    Would you agree that the acceleration on a moving charge in an electric field is independent of the direction of its velocity, but not for a magnetic field?

    Reply

    1. There is no “fundamental” difference; the right statement is that there is an electromagnetic force, of which electric and magnetic forces are different parts… and in particular, what one observer sees as a pure electric force will be viewed by another observer, moving relative to the first one, as both electric and magnetic.

      The force law that describes a particle moving in an electric and a magnetic field, from the point of view of any (inertial) observer, is

      F = q (E + v x B)

      F is the force (a vector), E is the electric field (a vector), v is the velocity (a vector), B is the magnetic field (a vector), and “x” is a “cross-product”.

      Notice that velocity does not appear at all in the term involving the electric field.

      So the acceleration of a charge, whether moving or not, FROM THE POINT OF VIEW OF AN OBSERVER WHO VIEWS THE SITUATION AS CONTAINING ONLY AN ELECTRIC FIELD AND NO MAGNETIC FIELD, is entirely independent of its velocity, both direction and speed. A different observer, moving relative to the first one, will see both electric and magnetic fields, and draw a different conclusion.

      Reply

      1. I don’t think this is correct:

        “So the acceleration of a charge, whether moving or not, FROM THE POINT OF VIEW OF AN OBSERVER WHO VIEWS THE SITUATION AS CONTAINING ONLY AN ELECTRIC FIELD AND NO MAGNETIC FIELD, is entirely independent of its velocity, both direction and speed”.

        Yes, on the RHS there is no velocity term associated with the electric field, but the acceleration term on the LHS for the force does involve velocity:

        F = d/dt (m_0 \gamma vec_u) = (m_0 \gamma^3/c^2 vec_u_dot_vec_a) + m_0 \gamma vec_a

        Although the magnitude of acceleration vec_a is velocity dependent, it’s direction is the same as that of the term on the RHS which is independent of velocity for the electric field term.

        Reply

        1. You are correct; I answered a question about the *force*, but as you point out, your question was about the *acceleration*. However, the issue you point out has nothing to do with electricity or magnetism; it has to do with space and time, and is present both for electric and for magnetic forces, as well as any other forces that might be present, such as the weak nuclear force or Higgs force. Newton’s law was F = m a; in this context both the F-side of the equation (which has to do with electricty and magnetism) and the “ma”-side of the equation (which has to do with space and time) are modified.

          I don’t think, therefore, I understood the nature of your question; what is it that you are trying to understand?

          Reply

    1. The Higgs force, like gravity has no charge. Anything that interacts with the Higgs field feels the Higgs force. This includes the stuff we’re made of (Electrons and quarks.) as well as many other particles like Tau leptons.

      Reply

      2. I don’t think I would say it this way. Energy and momentum are gravitational charges; the energy-momentum tensor is the corresponding conserved current.

        The Higgs force you can think of, if you want, as being due to “Higgs charge” (these are just the Yukawa couplings). But the main point is that, unlike the charges in the electromagnetic, strong nuclear, and [to a limited extent] weak nuclear forces, those charges are not conserved.

        Reply

        1. Interesting. Is there a reason why the weak and Higgs forces’ charges are not conserved? Would it be possible to have a force with two charges like electromagnetism not have conserved charges with a physics similar to that of our universe?

          Reply

          1. This only has a technical answer; sorry for non-experts.

            1) Higgs forces are from a spin-zero field; there’s no associated conserved current. Spin-one fields always come with a conserved current, for their very consistency; this is true of all the other non-gravitational forces. The weak force, however, is complicated by the fact that the W and Z are massive; this means that charge is still conserved but in a non-obvious way, because charge can disappear into the vacuum. It’s the same with electric charge in a superconductor; charge is still conserved but it doesn’t look that way because the vacuum is full of Cooper pairs, and the photon acts as a massive particle.

            2) I’m confused by this question; not sure what you mean. “Two charges”?

            Reply

        2. Thankyou for your reply. The answer to my first question makes sense and answers my second question as well.

          Reply

    2. What is charge? This is a language issue.

      I was charged 10 dollars for the movie and 100 dollars for the dinner. “Money” is a universal charge. Yet, in general, different action demands different charge. As “no money, no fun”, it is the same that “no charge, no action”. If a force without a charge, it can produce no action.

      Yet, what is charge? Charge is the “measurement” for the action it has done. That is, “charge” is in fact a “measuring ruler”.

      What is e (electric charge)? Well, what is “e” measuring? “e”-charge measures the “size” of the “causal universe”. The part of this universe beyond this causal universe is called beyond the “event horizon”.

      What is m (mass-charge) measuring? “m”-charge measures the “size” of the internal “envelope”, such as the quark-envelope or the proton-envelope. If there are envelopes beyond the event horizon, m-charge will measure them too. That is, the m-charge has the power going over the event horizon. If there is an invisible envelope, m-charge will measure it too.

      Reply

      1. You wrote : ““e”-charge measures the “size” of the “causal universe”.”

        No it doesn’t. Electric charge of a particle simply tells you how powerfully a particle will distort the electric field in its vicinity. Just as mass (actually, energy and momentum, in Einstein’s theory of gravity), tells you how powerfully a particle will distort space-time (said another way, distort the gravitational field) in its vicinity.

        Reply

        1. Indeed, the “e” itself does only what you said. But the “causal universe” is precisely defined by its squire (the photon). Thus, the boss got the credit. This is the same as a king whose legs do not go out of the palace takes the credit for everything happened in his dominion.

          Reply

    3. Umm… it’s the `Higgs charge’, but we generally don’t call it that for historical reasons. And the Higgs force acts on all particles that interact with the Higgs field… which also happens to be all of the known elementary particles that have mass.

      Reply

  38. OK, I think I understand why strong forces are hard to deal with a lot better now. However, this raises a bunch of questions I’m not really sure how to formulate. This gives rise to 3-body or n-body problems, right? How then do the dualities linking the strong regime of some theory to a weak one of another work? Linking something complicated to something simple doesn’t generally sound like it could work. Presumably this says something deep about one of the more surprising (to me) dualities, gravity / Navier-Stokes. The ABC conjecture also comes to mind as a weird thing linking the simple to the complicated.

    This is probably pretty unclear post, but I really have too vague a sense of what puzzles me to ask a sensible question.

    Reply

    1. “Dualities” which allow you to write a very strong force’s behavior in terms of a very weak one are remarkable, complex, quantum mechanical, hard to explain, and in most cases are not well-enough understood even to state clearly.

      I have not covered this issue on this website for a reason!

      I’ll cover this someday, but not now. However, here’s a hint. Protons and neutrons are incredibly complicated, with all sorts of internal structure. Yet the interactions between protons and neutrons, at least if you keep all the motion- and interaction-energies (i.e. kinetic and potential energies) below 1 GeV or so, are pretty simple — which is why the residual nuclear force isn’t that complicated and one can do a reasonable job with a semi-quantitative description of nuclear structure. Now how did that happen? Shouldn’t it be the case that if something is really complicated, everything you make out of it should be really complicated too?

      Apparently not.

      Well, this isn’t enough of a real answer, but a proper answer would take much, much longer, with many pictures.

      Reply

      1. Well, structures that make some quantity add up to zero is an obvious example where you lose complexity. Or more accurately, hide some complexity. Having an n-body problem on one side of a duality become “something simple” on the other side wouldn’t hide anything but show that the complexity of the whole thing is a mirage. (Side note; checking Wikipedia for n-body problem, it seems a solution is known to be impossible only for some specific method. I thought it was more general)

        Looking forward to the explanation with many pictures. Linking to a N A-H paper with a hundred weird diagrams is cheating 😉

        Reply

      2. One loophole that occurred to me is that since the situation is quantum, the extra stuff probably has a smooth distribution of probabilities that could add up to something simple although the classical case would be messy.

        Reply

  39. Matt: “… Clearly there is a language difference here… as is often the case with words in English and words in Physics-ese.
    … to understand that this way of talking about the strengths of forces is the best one to use.”

    There is no issue about the accuracy of this article. Yet, indeed, the “language” can make a big difference for the same story. In my view, the four known forces can be described with a set completely different language. That is, we can view these forces in their functionalities instead of their strengths. Then, these four forces can be classified into two types.

    a. Envelope constructing type:
    i. Strong force (SF) — constructing the envelopes for proton or neutron. Then, the residual of SF constructs the envelopes of nuclei.

    ii. Electromagnetism force (EF) — constructing the envelopes of atoms and molecules. Then, it also constructs the envelopes of the “causal universe”.

    iii. Gravitational force (GF) — constructing the envelopes of large mass bodies. Then, it also constructs the envelope of a non-causal universe.

    b. Envelope penetrating type: It goes into an envelope or breaks out from one, the Weak force (WF).

    The above description can also be viewed in terms of an automobile, as the universe is evolving “forward”. The constructing type is the “forward” gears while the penetrating type is the “reverse” gear.

    Then, we can go one more step; viewing these forces are building an amphitheater (without ceiling and walls) with chairs and stages, similar to the universe with quarks, nuclei, …, galaxies, etc.. The constructing force are “making” chairs, sections, …, stages. The penetrating force “brings” audiences and actors from one chair to another or from one section to a different one. That is, the WF is the usher of the theater.

    In the case of unifying these forces, knowing their functionalities are much more important than knowing their strengths. Even if their coupling strengths are exactly the same, they can still be completely different forces. Yet, knowing their strengths converge at some certain situations is still a great knowledge about them.

    With this amphitheater model, the forces classification (degeneration) is the results of that theater’s framework and functionalities. That is, there is a “fundamental/emergent” relationship, or the force-genealogy as follow:

    Force (degenerated) = K (degenerated) F(unified), K is the coupling constant.

    F (unified) = ħ / (delta T * delta S) ; T, time; S, space.

    This unified force equation shows the “sources” of all degenerated forces. The degenerated K (couplings) is caused by different “charges” (job-types).

    With different language, a story can be told differently. In this story, the alpha (α) is not only the coupling constant for electromagnetism but is the “manager” for all other charges, as it is a “lock” which locks the three most fundamental nature constants (ħ, C and e).

    Reply

  40. Great article, many thanks Professor.
    Just a couple of questions, I always had problems trying to understand what a force really is. I mean, what is the underlying mechanism that makes two particles affect each other. Is the same mechanism for all forces? what’s the internal difference between a repulsive and an attractive force? If gravity is “just” a distortion of space-time, what is a graviton?
    Thanks again

    Reply

  41. “the time it takes between one vibration and the next — which I like, poetically, to call a particle’s “heartbeat” — is equal to hc/m”

    but the dimensions of that expression are L^3.T^-2

    Isn’t it t=h/mc^2? (from E=h/t=mc^2)

    Reply

  42. In fig.2 , what do you physically mean by the abrupt stop of the strong force curve ? i guess it somehow must drop to meet the x-axis somewhere …..

    Reply

    1. In that figure the strong force curve does not ‘stop’ or go to 0; quite the opposite. It becomes so large that our way of describing it (In this article) breaks down. This is because when a force passes the ‘1 mark’ on that graph things become quite complicated.

      Reply

  43. Hi Matt,

    Although I learned a great deal from your article, as I always do, I didn’t actually learn the thing I was most hoping to! Basically, I’ve long wanted to understand why QFT uses the concept of ‘force’ at all. In what sense is it helpful to think of an electron and a positron pulling on each other, for example?

    In Quantum Mechanics, one can formally recover Newtonian concepts because it uses a Hamiltonian formulation (albeit with operators rather than numbers), but QFT uses something totally different (and something I’m not very familiar with). As a specific example, in QFT an electron and positron are supposed to attract each other by means of an exchange of photons. Yet such an exchange, if taken literally, would lead to repulsion rather than attraction, so Newtonian thinking seems totally misplaced here.

    I’ve always preferred the term ‘fundamental interactions’ rather than ‘fundamental forces’, because I just can’t see where their force-likeness comes from. This is especially so in the case of the Weak Interaction, which seems to always manifest itself transformatively rather than kinematically.

    I guess another article explaining what attraction and repulsion (and hence ‘force’) mean, and how they happen, in the context of QFT would really hit the nail on the head for me. If you have already written such an article, I’d really appreciate you pointing it out!

    Thanks again for all of your great work here.

    Reply

    1. You are right that “interaction” is a much better term than “force” — and when speaking to professionals, that’s what I use. But I haven’t yet written the article that explains why professionals do this! I think the term “force” remains necessary for communicating with non-expert audiences, because “force” has some intutive reach and some connection with freshman physics and many books, while “interaction” is too broad and vague a term to touch any intuitive concept.

      With regard to this issue, I do indeed plan to write the article that you’ve just suggested.

      Meanwhile, don’t forget the weak nuclear force (umm, interaction) does have a Z boson, and that does give an honest-to-goodness force too, just the same as gluons and photons! If we ever discovered a heavy weakly-interacting stable particle, and could make a bound state out of it and its anti-particle, the Z-boson-induced force would be measurable.

      Reply

      1. Given that a popular model of dark matter is WIMPs, would the z-boson mediated force have any consequences? Would it be strong enough to cause disparate dark matter particles to collapse under certain astronomical circumstances?

        Reply

        1. 1) the Z-boson mediated force could have been the one that made WIMPs bounce off an atomic nucleus. But in this case WIMPs would probably have been observed already. It appears something weaker, like the Higgs force, may have to do the job – if anything.

          2) No, a short-range force can’t affect dark matter particles that are macroscopic distances apart. In fact it could barely affect them if they were packed together. Think about how ineffectual electromagnetism would be if its range were 10^{-18} meters.

          Reply

  44. Excellent article.

    Question: If one particle emits or absorbs a virtual force carrier particle, shouldn’t that also affect its spin due to conservation laws? Or, in case of W boson exchange, always result in both interacting particles being “changed” (as W is charged)?

    Reply

    1. To really do this justice requires another article, which I do plan to write.

      To your first question: No. The problem is that virtual particles aren’t particles http://profmattstrassler.com/articles-and-posts/particle-physics-basics/virtual-particles-what-are-they/ — they operate under more general rules — and it isn’t really particles that carry forces, it’s disturbances in the corresponding fields. In fact you already know this from freshman year study of electric fields, which are, after all, spin-1 fields.

      It is really the Z that you would say generates the weak force, and the W, which really does change things, typically leads to decays.

      In the case of W boson exchange, yes, both interacting particles are changed, and typically that means that you can’t think of multiple exchanges as a push-or-pull force.

      In the case of gluons, both interacting particles are changed too, but in a way that is unobservable, does not lead to decays, and just maintains the push-or-pull force effect.

      Reply

      1. “electric fields are spin-1 fields” -> what do you mean by this? Do you mean, “electric fields” are made of spin-1 photons? with coherent quanta (=real photons) or without coherent quanta(=virtual photons, or disturbances?))? and why do you have to call “fields” spin-1, 0, 2 etc.? Intrinsic “spin (0, 1/2, 1, 2 etc.)” is associated with “a particle” but you can measure “spin of fields” without a real particle? or can you calculate? talk about? “the spin of fields(?)” without any real particle in the field? why this is so?(if “electric fields are spin-1 fields” is the bottom property/current understanding of the field, then give a few specific “simple(simplest)” examples that demonstrate why spin-1 field (but not spin 1/2, 0, or 2) is required for (and also is consistent with) explaining these examples(=physical phenomena in electric fields))? Massless virtual photons also have spin-1? Do massive? photons in superconductor? also still have spin-1? (“..It’s the same with electric charge in a superconductor; charge is still conserved but it doesn’t look that way because the vacuum is full of Cooper pairs, and the photon acts as a massive particle.”)

        Reply

  45. As far as i remember you previously told that the Higgs particle is not a force carrier , then what is the fifth force- force carrier ?

    Reply

    1. The Higgs particle would be called the force carrier of the Higgs force, as the photon is called the force carrier of the electromagnetic force. I don’t really like the term “force carrier”; that article has yet to be written though.

      Reply

  46. Excellent article. I have two questions.(1) Your fig. 2 shows the strengths leveling and not coming together as required in grand unified theory. Is it that they will come together on left of y-axis eventually?
    (2) Where do you put dark energy repulsion (lambda force)? It is hard to believe that something affects only at the galactic scale and there is no trace of it at the microscopic scale. Thanks.

    Reply

    1. (1) on the one hand, yes, grand unification is far to the left of the plot. BUT also there are subtleties hidden in that grey box. And the slow drift of the strengths of the forces is essential to the idea. The Higgs force does not get unified with the others in Grand Unification, nor is gravity. Any further unification would occur at even shorter distances…

      2) dark energy repulsion has no trace at the microscopic scale. It’s not a repulsion between objects. It is causing space itself to slowly expand, and this is very hard to detect on terrestrial scales.

      Reply

      1. Thanks. But something like lambda, may be having much larger value than the current small value of lambda (inflaton or whatever you call it) generated exponential inflation in the beginning. Would that not have microscopic implications in terms of forces?

        Reply

        1. No. [I assume by “lambda” you mean the cosmological energy density or cosmological “constant” (which isn’t always constant but ok…). It’s Lambda, usually.]

          If what you’re asking is whether the physics was that generated the cosmological constant (or assured it was large enough in early times to generate inflation and is now very small) might be associated with microscopic forces, then the answer is yes, it might, but there’s no guarantee. The cosmological constant itself is not associated with any microscopic effects; it is a large-scale effect, not a small-scale one.

          Reply

          1. Thanks . I see what you are saying. But I still find it incredible that some very large field gave rise to tremendous inflation, then turned off and no remnants left for 13.8 B years!

            Reply

            1. The equations say that this can happen.

              But first, you should not say there was no remnant of any sort. The energy density from that period of inflation heats up the universe, when inflation ends, and gets the hot-dense period of the Big Bang going! So it’s not as though there was no effect!! There’s just no microscopic force from that effect.

              However, if that energy density came from a standard inflaton field, all that is required to end up with no microscopic remnant is that the fields involved have particles that are very heavy and unstable. That means there aren’t any of those particles left, because they all decayed away; we aren’t able to produce those particles at our accelerators, because it would require too much energy per collision; AND the forces they generate have too short a range to have any effect on any current microscopic measurement we can make.

              Reply

  47. Really great , thanks Matt.
    You explained the Higgs force properties , but i could not find whereabout of its function since all the micro-world was already described by QFT and QCD….. so what ADDITIONAL function this force perform ?

    Reply

    1. It doesn’t really play much of a role in daily life or in the structure of the universe as we know it so far. That said, it might end up being how we discover dark matter. Of course it may have some functions we don’t know about. But under normal circumstances, everything that it could do is dwarfed by effects of other forces.

      Reply

  48. One nagging question that remains for me: what is it about the weak force that causes it to mediate a lot of particle decays? Is that just because of neutrinos and lepton number conservation or is there something deeper?

    Reply

    1. It’s deeper, and a long article is needed. It’s related to the Higgs field, the fact that the W and Z have masses, the fact that up and down quarks have masses (not only that, different masses), and a lot of other things. The buzzword is “symmetry breaking”, but since there was no real symmetry and it really isn’t broken, it’s not a good buzzword to hang one’s hat on… Stay tuned.

      Reply

  49. What would be the Higgs force acting between the virtual particles in empty space – the sea of quarks and anti-quarks. Since Higgs force is always attractive and does not cancel, out, the interactions between the constituents of QCD vacuum may have some effect. Can we then think of it as the “surface tension” of vacuum space. If the vacuum energy (zero point energy) is not constant between different parts of space time, what would be the impact of this Higgs force between the virtual particles. Even though Higgs force does not act at long distance, since the distance between virtual particles is rather small, wouldn’t this have a cascading effect again similar to surface tension for the vacuum space. We may not be able to perceive this because we cant feel the space because of relativity but its effects may influence expansion of space itself in cosmology

    Reply

  50. An excellent and informative article as always. It answered a question i didn’t even know I had. Two questions remain for me however:

    1.) Is the weak force always attractive like gravity, or does it have opposing charges like EM and the strong force? I’m assuming the former.

    2.) I assume that while charged particles are not affected by atoms at a distance, as they approach closer and closer to an atom or other electrically bound system that becomes less so. If so, how would an electron within a hydrogen atom, closer than the bound electron behave?

    Reply

    1. Matt can probably explain these better than I can, but I thought I’d give it a shot:
      1. The weak force also has opposing charges. They’re more like the charges of the strong force than the charges of EM, in that just like the three independent “colors” of the strong force there are two independent sorts of charge in the weak force.
      2. Approach close enough to an atom and the electron and the proton indeed have an effect. It’s a bit like holding a bar magnet at a distance from the north pole of another magnet, in that as you get closer the two ends want to go different directions.

      Reply

    2. The weak force is like the strong nuclear and electromagnetic forces in that it can pull and push, but it has other things that it can do — in particular, it can cause decays. Requires a separate article.

      The bound electron pushes on the second electron, while the proton pulls on it. Which pushes/pulls harder depends on where precisely the second electron is. When the second electron is far away from both particles, the forces nearly cancel; when it is close in, then the forces don’t cancel at all. This is the usual story — even from freshman year — about electric dipoles.

      Reply

    3. A complete answer to your question 2 would be the entire academic subject of physical chemistry.

      The interaction of non-atomic electrons with an atom is exactly how chemistry happens.

      Reply
  51. Pingback: What is the “Strength” of a Force? | Of Particular Significance

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Search

Recent Posts

Buy The Book

Reading My Book?

Got a question? Ask it here.

Media Inquiries

For media inquiries, click here.

Order Waves In An Impossible Sea

Harvard Book Store
Amazon
Audiobook: Audible
Barnes & Noble
Powell's Books
Elliot Bay Book Company
Vroman's Bookstore