Matt Strassler [March 25, 2012]
The annihilation of particles and anti-particles gets a lot of press — it sounds mysterious and scary and exciting and makes its way into lots of science fiction — but this bread-and-butter process at the heart of particle physics creates a lot of confusion. In this article I want to start demystifying it a bit, by describing a few of the basic rules that determine whether a particle and anti-particle of one type, if they come close together, can turn into a particle and anti-particle of another type. This isn’t the full story of particle/anti-particle annihilation, but it will get you started.
What are anti-particles? I wrote an introductory article about anti-particles here. For our purposes today, this is what you need to know. In a world like ours (with quantum mechanics and Einsteinian relativity) it is a mathematical theorem that every type of particle has a corresponding anti-particle, with exactly the same mass. Actually, it’s not just a theorem: for all known particles the anti-particle has been observed experimentally, so we don’t need to have a debate about it.
(Note: When I use the term `mass’ on this site I always mean the quantity that long ago was sometimes called a particle’s `invariant mass’; in accordance with modern particle physics practise, I never use the concept of `relativistic mass’ on this site. All electrons have the same mass; all photons are massless; this is true no matter how much energy they have and how they are moving.)
However, for some particles the anti-particle and particle are the same: the antiparticle of a photon (a particle of light) is a photon. The same is true for the Z particle and the Higgs particle (assuming the latter exists.) On the other hand, the electron, which has negative electric charge (by definition), has an anti-particle called the “anti-electron” or “positron,” which has positive electric charge. [Do not confuse the positron with the much heavier and more complex proton!] This is true for most of the known particles: the muon has an anti-particle called an anti-muon; the up quark has the up anti-quark; the anti-particle of the positively charged W particle is a negatively charged W particle.
Now, a fact: if I put a particle and an anti-particle together, almost all their properties cancel. For instance, the electric charge of a muon (a heavy cousin of the electron) plus the electric charge of an anti-muon equals zero; the former is negative, the latter positive, but they are equal in size and so they cancel perfectly. The only things that don’t cancel are their masses and energies. Actually, that statement’s a bit tricky. Mass isn’t “conserved”; we’ll see in a minute that mass can appear or disappear, which is really good for particle physics. The only thing that is definitely going to stick around is energy. Energy is conserved: however much you start with, you will end with the same amount. If these things sound obscure, stay tuned; we’re going to watch them play out.
1. Muon and anti-muon turn into two photons
Suppose I have a shoebox that has nothing in it except a muon and an anti-muon that are just about stationary. Then the energy inside the box is just about equal to the mass-energy of the muon plus the mass-energy of the anti-muon. [I’m saying “just about” because I’m oversimplifying by ignoring the electric field between the muon and anti-muon; but trust me that this is a tiny effect of one part in 10,000 that we can ignore for current purposes.] Let’s call the mass of the muon “M”; then the mass-energy of the muon is M c2, and the same is true for the anti-muon; and both have zero momentum since they aren’t moving. So the total energy E and momentum p in the box is initially just about
- Einitial = 2 M c2
- pinitial =0
Meanwhile everything else in the box is zero: the total electric charge is zero; the total angular momentum is zero; there aren’t any other things that are non-zero. Just the energy. And the mass, but they’re related.
Because almost everything cancels, it is often possible for a particle and its antiparticle to transform, through the action of one of the four known forces, into another particle and its antiparticle. For instance, the muon and the anti-muon could transform into a photon and a second photon (remember, the photon is its own anti-particle.) The photons will both have some energy; how much exactly? Well, the two photons are similar so they will have the same energy, and since energy is conserved the total final energy will be the same as the total initial energy, so
- Ephoton = 1/2 Efinal = 1/2 Einitial = M c2 = Emuon
Wow. Notice what amazingly cool thing has just happened: we started with massive particles, each motionless and so having no motion-energy, and having mass-energy M c2. But we ended up with two massless particles, with no mass-energy, but with motion-energy equal to the muon’s mass-energy: M c2. See Figure 1.
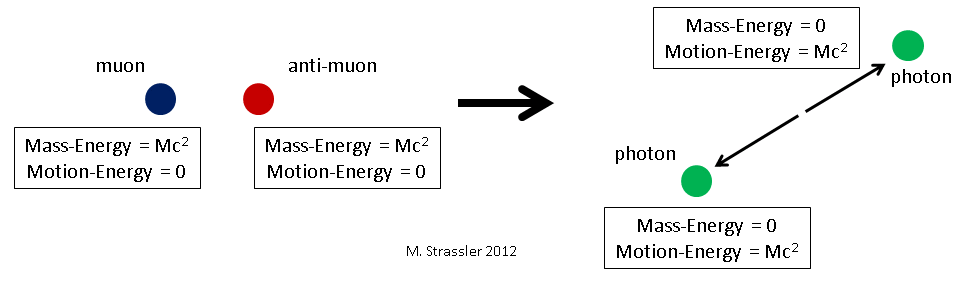
The photons will also each have momentum. But the momentum of the two photons will be opposite each other, and the total final momentum will add up to zero.
- pfinal = pinitial = 0
Notice that energy is conserved, momentum is conserved, but mass is not: the final mass is zero, even though the initial mass is 2 times M.
2. Muon and anti-muon turn into an electron and anti-electron
The basic reaction
- particle 1 + anti-particle 1 → particle 2 + anti-particle 2
isn’t the only possible process that can happen when a particle and anti-particle annihilate, but it is a very common one. Let’s look at another option for particle 2.
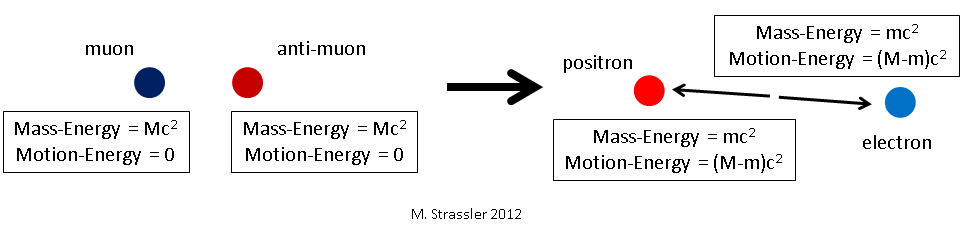
Instead of becoming two photons, the muon and the anti-muon may instead transform into an electron and a positron (an anti-electron), as in Figure 2; both the electron and positron have the same mass, which we can call m. (The electron mass m is about 200 times smaller than the muon mass M.) It is random chance (but with probabilities determined by quantum mechanics’ equations) that determine whether a given muon and anti-muon will turn into photons or into an electron/positron pair.
Exactly the same logic we used above leads to the same conclusion; by symmetry, the electron and the positron, which have equal mass, will emerge with equal energy, and by conservation that energy must be the same as the initial energy of the muon
- Eelectron = Epositron = 1/2 Efinal = 1/2 Einitial = M c2 = Emuon
So this is a little different; we started with massive particles, each motionless and so having no motion-energy, and having mass-energy M c2. But we ended up with two massive particles, each with a bit of mass-energy m c2 and a lot of motion-energy, with the electron’s total energy equaling the muon’s mass-energy M c2. And again, for the same reason as above, the momentum of the electron cancels the momentum of the positron:
- pfinal = 0
And of course their electric charges cancel too; there was no electric charge in the box before the transformation, and there is none after. Again, energy is conserved, momentum is conserved, charge is conserved, but mass is not; the initial mass was 2M, the final mass is 2m.
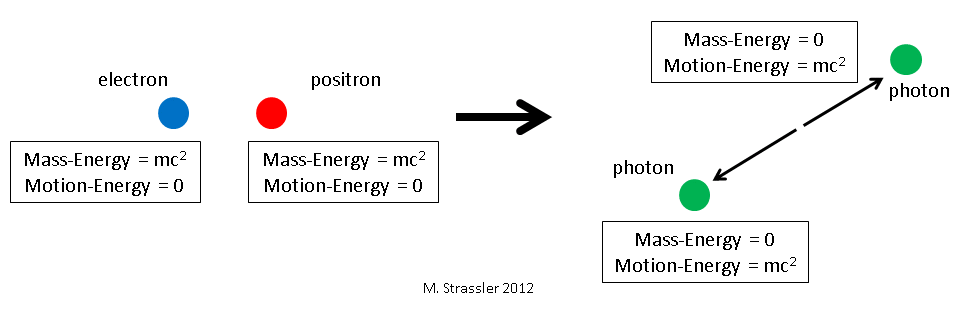
3. Electron and anti-electron turn into two photons
An electron at rest and a positron at rest can turn into two photons, just as a muon and anti-muon can. In fact we can do the whole calculation just by going back to the muon case, and in all the discussion and the equations replacing M by m. There’s really no difference (compare Figure 1 and Figure 3.)
4. Can an electron and anti-electron turn into a muon and anti-muon?
No. And Yes. What I will explain in a moment is that the answer depends on how you ask the question:
- No, if the electron and positron are initially at rest. There isn’t enough energy to make a muon and an anti-muon, so the process cannot occur.
- Yes, if the electron and positron have large amounts of motion-energy and hit each other head on. As long as there is enough energy to make a muon and anti-muon, then this process can occur.
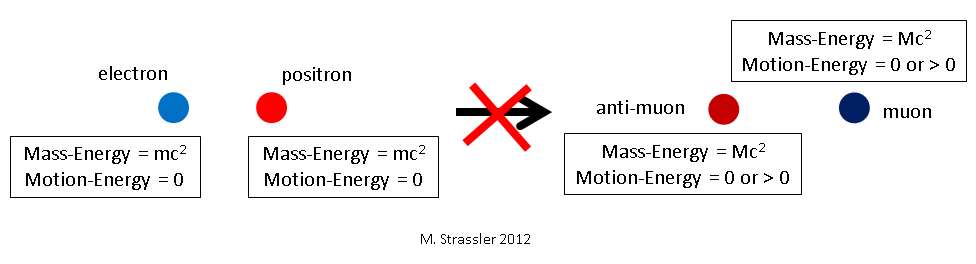
Ok. First, let’s convince ourselves that if the electron and positron aren’t initially moving — if they have no motion-energy to start with — there is no way they can turn into a muon and anti-muon. The logic is terribly simple; all we have to do is go back to the previous case where we considered a muon and anti-muon turning into an electron and a positron, and everywhere exchange muon for electron, anti-muon for positron, and M for m. This gives us
- Emuon = Eanti-muon = 1/2 Efinal = 1/2 Einitial = m c2 = Eelectron
But this equation is impossible! A muon has mass-energy M c2 plus its motion energy, which is positive. And M is bigger than m. This gives us a contradiction:
- Emuon = M c2 + motion-energy ≥ M c2 > m c2
In short the muon’s energy cannot equal m c2, as the conservation of energy (the second-to-last equation) would demand, because M is larger than m. Faced with this contradiction, we must conclude: this process cannot occur (Figure 4.)
However, the very way that this effort fails reveals how it may be acheived. For we need not consider electrons and positrons that are initially at rest. Let’s accelerate them — speed them up to near the speed of light, so that their motion energies are very large and their total energies (mass-energy plus motion-energy) are much larger than m c2. To keep things simple, let’s imagine we’ve made their initial energies exactly equal to M c2 ; then the total initial energy in the box is 2 M c2, and so for the process to occur the conservation of energy demands
- Emuon = Eanti-muon = 1/2 Efinal = 1/2 Einitial = M c2 = Eelectron
which is no longer in contradiction with the requirements of the previous equation, Emuon = M c2 + motion-energy ≥ M c2 > m c2. In fact, the electron and positron’s energies are in this case just barely large enough to a make a muon and an anti-muon at rest (Figure 5.)
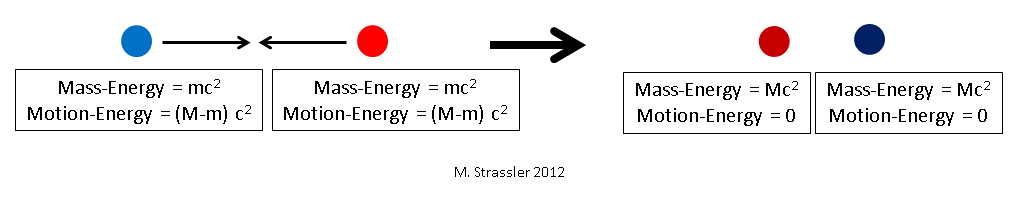
If we make the electron and positron’s energies even bigger, then they can still make a muon and an anti-muon. The excess energy will go into motion-energy of the muon and anti-muon; see Figure 6.
And notice again that mass is not conserved, even though energy is. In this case, the mass has gone up, from 2m to 2M. This is really important for particle physics!!! This is one of the main techniques that we use for discovering new particles; we smash a particle and its anti-particle together with very high motion-energy, in hopes that they will turn into a heavy particle that we’ve never before observed, along with its anti-particle.
Summary
- A particle and its anti-particle that are stationary can annihilate to make a particle and its antiparticle as long as the initial particle is heavier than the final particle.
- A particle and its anti-particle that are stationary cannot annihilate to make a particle and its antiparticle if the final particle is heavier than the initial particle.
- A particle and its anti-particle that are moving relative to each other can annihilate to make a heavier particle and its antiparticle if they have sufficient motion-energy.
- If the mass-energy plus the motion-energy of the particle equals the mass-energy of the heavier particle, then the heavy particle and anti-particle pair will be produced stationary.
- If the mass-energy plus the motion-energy of the particle is greater the mass-energy of the heavier particle, then the excess energy will go into motion-energy of the heavy particle and anti-particle pair.
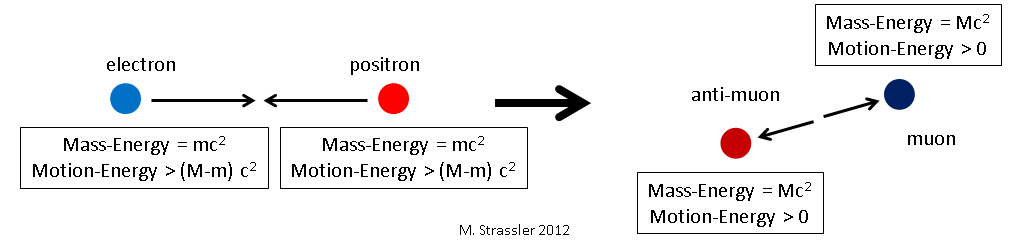
Fig. 6: As in Figure 5, but with even more initial energy in the electron/positron pair; the excess energy not needed to make the mass-energy of the muon/anti-muon pair goes into their motion-energy.


160 Responses
I am uncomfortable with your assertion that mass is not conserved (eg. in section 1) because “the final mass is zero”. While it is true that each photon, individually, is massless, a system comprising multiple photons moving in different directions has non-zero mass. The invariant mass of a composite system is not the sum of the rest masses of the parts, unless all the parts are at rest and are unbound by mutual forces.
The system you show comprises two photons moving apart with equal and opposite momentum. Taken together as a system, whose boundary is defined by your “shoebox”, the two-photon system has an invariant mass of 2Mc^2. I don’t have an authoritative reference to give for that, but the wikipedia page on “Invariant Mass” covers it in a way I believe to be correct. It is this which can be compared with the initial state (two muons in a shoebox) which had an invariant mass of 2Mc^2, and sure enough, the mass of the system is conserved. What you have done in the last sentence of section 1 is to neglect the shoebox defining the system, treat the photons as free individuals, and so end up comparing unlike things which are not alternative states of the same isolated system.
As you state on other pages of your site, the mass of a system is not the sum of the masses of the components. So why do you add up that sum in this case (two photons of zero mass) and declare that “the final mass is zero”? It’s calculations like that which have caused endless confusion over the years and led many to explain the difference by the voodoo process of “converting” mass into energy. Rest masses are not additive; get over it, and stop doing these kind of sums. Any time you are looking at a body comprising more than one elementary particle, you have a system, and you need to define consistent boundaries for it and stick to them. When you do so, the only mass that is physically meaningful is the invariant mass of that system. If that system is isolated, you will then find that mass is conserved, whatever reactions go on inside it.
He says in the article that when he means mass, he means what invariant mass meant long ago, not what it means now.
Hello Sir, I am so much interested on the topic above, but I have one doubt, is there any experimental evidences for existence of pair annihilation? Please Reply…..
Thank you !
I find it interesting that although it is obvious that all matter particles, energy photons and even fields are composed of the same thing that is called energy, which is always conserved and can generate various different observable output results in interactions between such entities, such as the 3 dimensionally stable static mass effect of matter particles, the dynamic mass effect of energy photons that operates at ninety degrees to its direction of travel that varies in amplitude in direct relation to the frequency of the photon that generates the photoelectric effect by freeing electrons from their atoms if the photon’s frequency (energy content) is high enough, the ability of matter particles to stand still in relation to other matter particles, the constant motion of energy photons at the speed of light, etc. Since one entity (energy) creates the structure of each of these entities, it is apparent that this energy must be structured differently in matter particles than it is in energy photons, such that it generates properties in matter particles that are greatly different than those of energy photons, etc. I see very little explanation of what the basic energy structuring substance is composed of or how that substance is structured or built up in each of these entities in such a way as to generate its observed output results in interactions. It seems that people are satisfied to just note the output effects of photons and matter particles, etc. and the probabilities of occurrence of generation of each effect during interactions, etc., and the ways that each entity can be transformed into each of the others, etc., but care very little about the ways that the particles are constructed internally to generate those output results and how the transformation from one entity into another entity works internally within the entity. It appears to me that such an understanding and a workable model of how the mechanisms can work is not exceptionally difficult to accomplish. This has been done on the molecular and atomic entity scales, so why hasn’t it been done on the basic particle scale?
neither a Lon the particles and ANTIPATICLES generate particles or antitiparticles symmetrical that exist in ours lifetime,the spacetime could ttonbevreduced into the level of theirs energies,asked existence of others universe or dimensions
So people hear about how matter is never destroyed but just becomes a different form of matter. But you say that they produce energy which has no mass which means it is not matter. So are you saying that when they collide they are annihilated completely and take no new form but there is just two atoms in the universe that no longer exist?
So a particle and its anti particle annihilate on contact unless they are a quark and an antiquark, in which case they form particles of various types. So what then is an anti particle? I thought they were defined by this mutual annihilation? Why different for quarks?
Is particle/antiparticle annihilation a possible route to future ‘cold energy’ production?
i might not be a scientist but why cant we use this to generate electricity because when the electron and positron annihilate each other it generates one photon which could be used as a energy source right?
Takes more energy to create and confine antimater then you get out
Non of this shit makes sense to me
But there is complete symmetry in the onyeractions between and positron?prof strassler.bu is not stramge that amtimayter had ,issed on the universe and just remain amtiparticles.the transformation of mass and emergy near the speed of light would be conserbed,necause the space and time are asymmetrics? Why the uniberse is not only one energy?
Please stop people have real questions and comments for Matt and you keep clutering up the site with your insane musings
Dear Professor Matt Stressler,
According to Fig. 3: The annihilation of an electron/positron pair to two photons – is there any real experiment which was done by using free electron and free positron in an isolate system? Thanks.
Nimit.
Do not exist antimatter in the nature.the antiparticles are subprodutos of transforma tios of mass into energy and viceversa due to the transformstion is not complete conserved because of the se transformstion o curso neurastenia of speed of light.then the antiparticles are generated by the asymmetry of matter and spacetime, than lead us tô the contra ti onof of spacetime and time dilatation, it due the pt symmetry breaking generating the speed of light as constant and violation of cp. The antiparticles the are negative energies of spacetime are energy locally bundleled
ed in “Ho
es” in the spacetime.
Bad english and silly ideas is all you seem to be promoting in your comments
“However, it happens that we are made from particles which DO have distinct anti-particles. And that means that anti-matter is distinct from matter. At that point we can notice that our universe seems to have very little anti-matter in it — hence the puzzle — how is it that in the early universe a tiny asymmetry of matter over anti-matter was created, leading today to our universe with a tiny bit of matter and almost no anti-matter? This is the puzzle that theories of baryogenesis attempt to solve.”
Some years ago I read an explanation of this “asymmetry of matter over anti-matter” in the early universe based on simple logic. At or around the Big Bang trillions of particles and anti-particles were created simultaneously (presumably because Time didn’t exist yet!) in equal numbers but randomly distributed. Randomness is clumpy: given a ‘heads-or-tails’ option, long sequences of heads (or tails) are not uncommon. So there had to be areas of early space where both matter and antimatter particles clustered, shielded a few of their kin, and prevented/delayed (has Time started now?) the total mutual annihilation of opposite pairs. By sheer chance there were more, or larger, clumps of what we call ‘matter’, and somehow these established a material environment that forever-after favoured the prolonged existence of at least some matter particles, alongside the continuing process of particle-antiparticle annihilation which you explain so well in this thread. Perhaps the conditions favouring a universe of sustainable matter only happened once, at the very start; but chaos theory would secure its continuance – sensitive dependence on initial conditions. Apologies if this angle has already been covered in another area of your blog. What do you think?
Have there ever been test results where both matter and antimatter were viewed AT THE SAME TIME. I mean both partners at the same instant. I think that maybe only one particle is involved. Do to collisions, it goes out of phase 180 degrees and becomes antimatter. I know there are exceptions and complications. RON
How does the total entropy change before and after the (particle-anti particle) annihilation process?
My notion of space-time in the “quantum scale” is such that it’s bubbling with virtual particle-anti particle couples that come alive for the shortest blink of time in order to annihilate and disappear all but as soon as they appeared.
And, as far as I know, the black hole radiation is considered to come about as the “orphaned” half of a virtual particle-anti particle couple stays alive (as the other half falls in to the black hole).
Furthermore, the universe seems to be expanding in an accelerating speed, thus (maybe) reaching speeds where the structure of the space-time will “rip out”.
OK — what happens to the virtual particle-anti particle couples when the expansion of the space-time gets so fast that the couples get considerably far from each other in that tiny fraction of time that they exist??? Will they survive and become real?
What if the inflation stage of a universe is actually a result of the hyper-fast expansion of a previous universe as the speed is so great that virtual particles start becoming real and somehow “freeze” the hyper-fast expansion into something we now consider “young” (post inflation) universe?
I have a question that I didn’t see anyone bring up in the comments, so I’ll ask it. BTW, I know just enough to be dangerous… Anyway, if a positron and electron annihilation produces a pair of photons, has the reverse been observed? Do high-energy photon collisions produce electrons and positrons occasionally?
Sppot on with this write-up, I absolutely feel this site needs far morte attention. I’ll probably be back again to read more, thanks for the info!
Hi, I think your website could be having browser compatibility issues.
Whenever I take a look at your blog in Safari, it looks fine however,
when opening in IE, it’s got some overlapping issues. I merely wanted to provide
you with a quick heads up! Other than that, great site!
Bead blasting is very common for removal of paint or corrosion from metals, and iss a long-time favorite of classic vehicle restorers.
In reactive cutting, the high-energy beam ought to be used like associate element
torch to chop shapes out of steel plates. The Australian Dental Association recommends that
alll patients who want to whiten their teeth have a thorough dental check-up beforehand.
Most of the health problems we’ve discussed here arre euther radically improved or eliminated by eating a diet that meets the needs of a carnivore — one
which closely resembles the nutritional balance provided by a mouse.
Very descriptive blog, I liked that bit. Will there
be a part 2?
Great post. I was checking continuously this blog and I’m impressed!
Extremely helpful information specifically the last part
🙂 I care for such info a lot. I was seeking this particular info for a long time.
Thank you and good luck.
I’m new to a lot of these concepts and don’t have any background with math or physics. I greatly appreciate the work you’ve put into this website.
I’m guessing my confusion is arising because you had to simplify this for people like me but at the beginning of the moun and anti-moun scenario you said they were “just about stationary” and in the summary it says just stationary. Does this imply that the particles need some very small amount of motion energy for the annihilation to occur?
But wait my ignorance does not stop there, the thought that photons must have some miniscule amount of mass keeps working its way into my layman mind. Which leads to more dumb questions. I guess I’m also asking why is it so unlikely for photons to have some mass, wouldn’t they have to in order to be effected by gravity(blackholes)? Will appreciate even just a link, sorry I know I’m just missing something.
Ha, Matt, answered my own question about “where does mass go” by reading your prior articles (should have started at the beginning). We novices “know” the principle that “mass is conserved,” but haven’t understood that it’s the mass of a SYSTEM, not the individual components. (I understand your bold-faced emphases now….) This old English major got into this trying to figure out what energy is and having done that (sort of) wondering what the = in Einstein’s equation actually MEANS. Physics is fun and wonderfully mind-stretching. Thank you.
there is asymmetry between particles and antiparticles,for that reason part of energy is transformed in the osccilations of particles into antiparticles and viceversa that are given by breaks of rotational invariance( CP and PT ) and permit the existence of others spacetime continuos.the trasformations of energy into mass and vice versa not totally uniform or better conserved nearest of relativistics speeds( speed of light),the that is seen by the asymmetry of space and time
( generating the conjugation of space and time to spacetime continuos to 4-dimension manifolds with spin tensor- torsion ) that does appear the antiparticles as symmetry of the spacetime.
then the extradimensions permit neutrinos with superluminal speeds and strong violations of symmetry CP (PT)
this is not correct.
Novice here. Matt, are you saying mass is not conserved in some particle/anti-particle collisions? So what goes with the mass? Converted to energy?(!)
is much possible that the annihilation of particles and antiparticles must not conserve totally mass and energy,because there are others variables as spins that quantify spacetime-it is transformation energy into mass and viceversa-with alterations of mass with velocity.it is the time dilation and space contraction with violation of CP
Theoretically speaking of course
Can we be able to control the collisions that every time we get consistent results e.g electron with positron form photons with motion energy=mc^2 and how much mass will this energy be able to move(work done)(say we have a quadrilion of these electrons and positrons), In terms of rotating a turbine heating a substance, displacing a piston cylinder in a controled volume……i hope u get the question
If an electron and positron annihilate, how do you know how tiny the probability is for producing more than 137 photons? Won’t the final-state bosonic permutation factor begin to dominate over increasing powers of alpha so that producing another photon is highly likely, once you are over 137?
i think that the antiparticles are product of the four-dimension .This is the TIME.I t is of the 4-di,mensional spacetime continuum.then the occur the pt symmetry breaking,and the conseravation of charge is global. just is violated apparently.the antiparticles appear due the relativistic velocities,diffrences oribated in frames in relative motions.
THE STR WORKS WITH CONTINUITY OF SPACETIME,AND QM WITH DISCRETENESS.IS CORRECT?
It’s lile you haven’t even read Matt’s blog posts
Re your March 17, 2013 post (“What Feynman said…”): He also said (as you know) that the reason why there are antiparticles is roughly as “J” says in the March 26, 2012 post above. Do you think that this is genuinely an explanation of the existence of antiparticles? If so, what sort of explanation is this? For instance, physics sometimes explains one law of nature by deriving it from one or more other (more fundamental) laws, as when Newton explained why Kepler’s laws are (approximately) true. Newton’s explanation works by describing (not completely) the causes of planetary motion. But the “explanation” of the existence of antiparticles by appealing to special relativity and quantum mechanics does not seem to work that way. How would you characterize how it works, if it does indeed explain why there are antiparticles. (Recall that “The reason for antiparticles” was the title of Feynman’s 1986 Dirac Lecture.)
i accord in terms.i understood thyat the antiparticles doesn’t exist if the particles itself are asymetrics,and the antiparticles are substrxtum of that property of matter.
then cpt is not conserved,but the lorentz1s invariance is ,that is given by it lagrangean.
Over six years ago, from this forum discussion, a thought came to me that there is no such thing as ‘vacuum’ in the universe, and the universe is in a process of phase transition. The ordered phase is transforming into galaxies. All galaxies are in a macroscopic single state, much like super fluid He3 with no temperature. Outside galaxies, it is the disordered phase with a bone cracking cold temperature of 2.7 K, and light travels slower outside galaxies than inside galaxies.
With this thought, that there is a perfect plan wave running in the background of every galaxies, some deep puzzles in physics can be explained. Like the entanglement experiment of two particles, where the oscillatory state of each particle in no way can be determined, but when the relative phase of their oscillatory states is checked (entangled), and afterwards they have been separated thousands of miles apart, at that time, if the oscillatory state of one particle is checked, the state of the other particle can be determined with absolute certainty. These events of absolute uncertainty and certainty can’t be the act of individual particles but the act of a plan wave motion that may exist in the galaxy.
Recently, I went ocean fishing, where I saw speed boats running on ocean surface wave in a harbor. At certain speed, the up and down motion of speed boat became harmonic with the ocean wave and it started skipping the wave with a rhythm of its own. A particle as big as a speed boat can behave like a wave just by riding one, and it can do so at any speed, but for a particle to behave like a plan wave, it has to move at a speed that is an integer times the speed of the plan wave that it is riding on. It occurred to me that I had seen electrons doing just like that.
More than twenty years ago, I used to use Low Energy Electron Diffraction (LEED) routinely in my surface physics study. LEED is a simple device for checking surface crystal structure of a material. It has an electron gun mounted at the center of a half spherical screen and a voltage control for changing electron speed. The electron gun shoots electrons perpendicularly at a sample mounted in front of the gun, and the back scattered electrons form a diffract pattern on the screen. I was puzzled then by the fact that a sharp diffraction pattern is not observed with a continuous voltage change, but only at a set of 4-5 discrete voltages within a range of 0-200 volts. The voltage of the first diffraction pattern observed is around 10 Volt. At this voltage, from eV = 1/2mv2 , the electron speed out of the electron gun is 1.9 x 106 m/s. For electrons to act like a plane wave again at a higher speed, they have to double, triple or quadruple this minimum speed. As the voltage is proportional to the square of velocity, the set of voltages that diffraction pattern can be observed is, 10, 40, 90, 160 in the 0-200V range.
I remember that the voltage settings I used to use were around this set of values, but the settings varied from time to time. When I search online, there are also different set of voltages used. Actually, the variation of this set voltages from one LEED experiment to another is a better evidence that the electrons are riding on the galaxy wave. The 1.9 x 10 6 m/s minimum speed is not the speed of electrons in the galaxy frame but their speed relative to earth. Three factors may affect the speed of electrons in the galaxy frame. Earth surface velocity, which has a maximum value at equator, is only 460 m/s, that can be ignored. Earth orbital velocity around sun is 3 x 10 4 m/s, a factor about 1%, that may not be easy observable can also be ignored. Sun orbital velocity on the Milky Way plane is 0.2 x 10 6 m/s, that is a factor of 10% on electron speed in the galaxy frame. A 10% variation in velocity corresponds to a variation of 20% in voltage. This variation should be observable from one experiment lab to another, as the orientation of the electron gun is likely different from one lab to another. Even in the same lab, as earth rotates, the orientation of the electron gun with respect to the sun orbital direction changes during a day. If one takes a set of measurements of voltages that diffraction patterns are observed in the morning, and takes another set of measurements in the afternoon, and if a variation on the two sets of measurements is observed, one can be sure that one is seeing the galaxy wave in motion.
what the origin of antiparticles? never was seen antimatter until today?
antimmater curve the spacetime or would be curved by the spacetime? what is the type of curvatures generated by antimatter-if it really exist?- no believe that antimatter exist in the nature,think that its can to exist to compensate the conservation of energy and due the symmetry of spacetime-this to explain the time dilatation and contraction of space,or save PT still
Anti-particles are not theoretical speculation, they are established fact. They were discovered in the 1930s and are observed every day; in fact they are used in modern medicine: look up “Positron Emission Tomography”. And of course we use them in particle physics all the time; for instance, the Tevatron accelerator, which operated for several decades, generated collisions of protons with anti-protons.
Anti-matter particles do not have anti-energy, or negative energy; they have positive energy, just like particles do. (This is well-verified in particle physics experiments.) And so they should generate the same gravitational effects as particles. An earth made from anti-matter atoms would generate the same gravitational effects as our the earth does.
The point is that nature does not create antimatter. Not in our galaxy at least. To think that matter somehow ends up in one place and antimatter ends up somewhere else violates the second law of thermodynamics. All these particle and antiparticle experiments are proof that photon can’t create matter as there will be no net matter end up in our hands. These experiments are just another solid proof that mass can convert to energy and vise versa but mass is not matter. There is no real distinction between “relativistic” mass and “intrinsic” mass. A spinning top and an oscillating string when their motions are extremely fast may appear like solid objects and are much heavier than they are at rest. Mass is a notion of motion not a notion of matter. If photons can’t create matter, the Big Bang theory is false from start.
If we were microbes living on a dust ball embedded in an iceberg floating in Arctic Ocean, we would observe “cosmic” black body radiation coming all around us from the ocean water but not in the iceberg. We would also observe a red-shift of light coming from other icebergs even if all the floating icebergs were in some equilibrium distances relative to each other. This is simply an optical effect as light travels slower in water than in ice.
There may not be such a thing as vacuum but only a limitation of our ability to detect what is in the space. Particle and antiparticle pair production by photon scattering in space is a manmade “Brownian motion”. If we dismiss the possibility that matter is created this way by nature, the only conclusion left is that matter is there all along in the space we call vacuum. In the photon scattering process, the photon energizes the matter into different modes of motions of the same fundamental particle. Electrons and quarks are from the same particles that are motionless when they are in bound state in space. Mass, charge and spin are not intrinsic properties of elemental particles but different modes of motions of a more fundamental form of matter. We all expect to find a more fundamental form of matter but why do we expect to see that fundamental form of matter behaves the same as the forms of matter we know?
Ya I also have a bunch of baseless hypotheses perhaps I’ll follow your lead and write them here
On the subject of Feynman and past directed time travel; I believe that in the 1940s he and Wheeler did much to popularise the concept of advanced and retarded fields, in which radiation propagated in both directions through time, creating a web of cause and effect in both directions.
Is that idea still current in scientific circles?
No, it is not.
From where we observe our world everything “moves” from the past to the future.
Is it legitimate to think of particles “moving forward” into the future and antiparticles “moving backward” into the future? As for particles that are both particle and antiparticle such as the photon it’s seems that they are always massless and therefore necessarily move at the speed of light (c)
Now looking from the point of view of a massless particle/antiparticle “moving” at c, distance and time would collapse to 0 (I am assuming this only by my intuitive understanding Einsteins theories). If this is the case for a particle/antiparticle it is meaniless to think of it moving backwards or forwards into the future, but from where we observe the particle/ antiparticle will “move” into the future.
I am not sure if this way of thinking is compatible with the second law of thermodynamics but I has a nice symmetry to it.
— John
Many members of an entire class of particles, the mesons, are massive and their own antiparticle, being composed of a quark and antiquark. On a more fundamental level the Z boson is its own antiparticle.
Let’s see. First let me correct a misconception. The Z particle has a mass and is its own anti-particle; the same is true of the Higgs particle, and of a number of hadrons. It may be true of dark matter. So that idea’s got to be fixed.
Now, what does it mean to “move forward” or “move backward” in time? If you think this through very carefully you’ll find it doesn’t actually mean anything.
What Feynman said (and he is the source for this common notion) is that the math describing anti-particles moving forward in time is the same as the math describing particles moving backward in time. This is a statement about the math. Anything you actually measure involves measuring how a starting point evolves in time to an ending point. There’s no meaning, experimental or conceptual, to saying that anti-particles are particles moving backward in time. It is not as though experiments involving anti-particles would go backwards, with a result known in advance that is forgotten by the time the experiment is over.
Furthermore, and very important, there is no unique definition as to which is particle and which is anti-particle. We call the electron “particle” and the positron “anti-particle”, but that is a choice! We could equally well have called the positron “particle” and the electron “anti-particle”. There’s no way to say “this one moves forward in time” and “that one moves backward in time.” The correct statement is “the electron is the anti-particle of the positron and the positron is the anti-particle of the electron”. The same is true of the W+ and W- particles; each is the anti-particle of the other, and there’s no point in saying “this one is the particle and the other is the anti-particle”. This is where the true symmetry lies.
antimatter will do the spacetime to be curved?the negative curvature should imply the interne space of the universe,curved to into? the lifetime of antiparticles might be shorter than the proper time of particles.then the violation of T-reversal together with the violation of invariance of rotation(P),violation of PT or better the breakdown of pt or cpt.the invariance of lorentz imply the asymmetry of space and time as generate of spacetime,that is refered b y the differents observers.then the the time to the space curved is to T reversal or to progator forward and backward in time have differents metrics to the spacetime.the asymmetry of space and time is generated by the symmetry of connection of space and time into spacetime continuos that is into of 4-dimensional manifold
Antimatter curves space exactly the same way matter does. This is obvious from the fact that some particles are their own anti-particles; it would be impossible for photons to curve space at all if particles and anti-particles curved space differently.
A photon is its own anti-particle.
Does this mean that any photon/photon collision can be regarded as a particle/anti-particle collision, or is there some way in which photons and “anti-photons” are distinguished?
Do photon/photon collisions produce massive particles by change of motion energy into mass?
“Anti-photons” has no meaning. A photon is a photon. You can view photon/photon collisions as particle/particle or particle/antiparticle; since a photon is its own antiparticle, there’s no difference.
Yes, in photon-photon collisions, some or all of the photons’ energy can be used to make massive particles (and the rest can go into motion of those particles.) Some day there may be a photon-photon collider that can make Higgs particles in its collisions.
So does this make photon-photon collisions different from particle antiparticle collisions, or is it just a case of symmetry?
And if I have two narrow beams of light (say commercial laser pointers) at right angles to one another would their be enough collisions for me to detect their beams interacting?
“gravity electron-positron –> two gravitons (extremely rare but certainly possible)”
Where gravitons are their own are their own antiparticle, what do you get in an SMBH where they’re so closely packed that they regularly annihilate. Maybe this graviton-graviton annihilation process is why we see the skewed galactic gravitational effect we call Dark Matter? The above annihilation equation also suggests a massive graviton, how big is it?
Gluons are also their own anti-particles and also self-annihilate, for instance inside protons and in the proton-proton collisions of the LHC. It’s nothing special. It’s simply due to having sufficiently complicated equations, and it is not a big deal. And it doesn’t lead to either massive gravitons or dark matter.
The above annihilation equation only suggests gravitons have energy. Two massive particles (Electron-positron) can annihilate to two massless ones, so long as the energy balances. (The famous, E = MC^2 +pc^2)
My objection to this conjecture would be that we know spacetime can vibrate and we call these vibrations gravitational waves, (http://en.wikipedia.org/wiki/Gravitational_wave ) we have even built detectors to detect them (Which is difficult, they are very faint, I believe that with present technology only those produced by merging black holes would be detectable.)
It looks like that particles and antiparticles are annihilated because they are vibrations in opposite phase. Previously I though their relative phase is kept by the vibrations of gravity field. This may not be the case. We can’t talk about a vibration in a certain phase without a reference point. Like in a two phased electricity generator, we have to ground one end of each coils, then we can say the electrons in one coil are vibrations 90 degrees ahead relative to the ground and vise versa about the other coil. We may think all particles at their birth event are + 90 degrees ahead of the birth event, and antiparticles are -90 degrees before the event, in terms of time, particles are born at half of h/mc^2 second ahead of the birth event and antiparticles are born at the same amount of time before their birth event. The vibration phase is referenced to the time in the space-time event point. After their birth, a pair of particle and antiparticle will follow their own path in space-time, each of them will oscillate back and forth relative to the space-time event point at a frequency of mc^2/h. Yes, both of them are time travelers, both can travel to future and past, just not far. An interesting question is how do they keep their distinctive birth phase while travelling in space-time? I think the answer is simple yet amazing. It is simple because they have mass, they are bound to gravity. It is amazing because I never thought about the space-time in this way, they are not even visible, yet the binding of the particles to a space-time event point is so strong that even the particles are vibrating at billions of times per second, they never miss a step. Image that a particle was born some billions of years ago. On its path to our present time, it might have been fused together with other particle in a star, and later was blown off when the star became a supernova and exploded. After this enduring journey, it still bind to its space-time event point, and by chance, it ended up on the walls of a particle accelerator. By another chance, an antiparticle created in the accelerator happened to hit the particle on the wall, their paths merges together become one event point. Since both particles are bound to their event point so tight that they know they are vibrations on opposite phase, they annihilate each other.
“Gravity is space-time. If space-time can be curved by the presence of matters, it can also vibrate… the local vibration of all the matters (not the antimatters) are in synch with the local vibration of the gravity field…”
Again, please excuse my naivety on this subject, but the above concepts may support my prior conjecture regarding the ability of gravity/space time to vibrate at frequencies that are not in sync with matter near the point of modification by Super Massive Black Holes, which may establish a decaying space time field that only resynchronizes itself to be seen as Dark Matter at an intra-galactic distances from the point of modification and still later, further decays to express itself as Dark Energy at intergalactic distances as it reaches an even lower frequency that repulses matter in line with the wave vector.
I think there is a much simple model to explain particle and antiparticle. It is like two phase electric generator. We place two coils opposite to each other, connect one end of each coil to ground, and place a magnet on the shaft. If we crank the shaft in a full circle, one of the coils, coil A will generate a full cycle of electron oscillation. The other coil, coil B will also generate a full cycle of electron oscillation. As we have grounded one end of each coils. We can say that coil A is 90 degree relative to the ground and coil B is -90 degree relative to the ground. In this model, the frequency of electron oscillations in the coils are determined by how fast we crank the generator, but it does not need to be. One can turn the oscillation in coil A into anything one wants using some electric circuit, a square pulse for example. One can do the same thing for the oscillation in coil B, or even split oscillation into smaller oscillations in time. However, no matter what you do to the initial oscillations, their relative phase will stay the same.
We can think a high energy photon as local vibration travelling in space-time. If this photon is the one to create a pair of particle and antiparticle at a particular event, the last cycle of its vibration before its demise is used to crank the generator we have described. Just like the pulse A and pulse B generated in our model, the pair of particles generated in this way will always have a fixed phase relative to the ground, in this case, the gravity field. One can expand the simple model, there does not have to be just two coils, we may put three or four coils, and coils themselves may have complicated structures.
There need not be a pair of particles; I can create a neutron-antineutron pair, then let the antineutron decay to an antiproton and positron. Now neither the antiproton and positron have a ‘partner’; we have created an antiparticle without a particle to pair with it. The two antiparticles can then annihilate independently.
I think the ‘opposite phase’ picture covers this pretty well, but the hole-mound picture is also quite intuitive. I would even argue that antimatter as entered our culture so that many laymen have the idea that antimatter is somehow ‘opposite’ and cancels out normal matter like positive and negative numbers.
Which one of the four forces is played in anihilation? Certainly not gravity and EM, Don’t seem like ordinary strong and weak force either.
This is rather like asking which of the fundamental forces are involved in light waves interfering. Annihilation is not related to any of the four fundamental forces, it is something that waves in a field do.
if you have a wave and anti-wave in any field and they meet, they will cancel. If you have a friend and a long rope you can send an up wave and down wave from either end of the rope and watch them cancel in the middle, annihilating (their energy being converted to heat.) In a similar way a particle and anti-particle will annihilate when they meet, in the same way they can reflect and interfere. It’s a property of waves in general.
Antiparticle and particle annihilation is far from any phenomena that can be explained using some intuitive pictures. I like intuitive pictures, double slits experiment is a good example. The fact that a single photo or a single particle can produce an interference pattern has become one of our intuitive notions about nature. Two photons or multiple photons can also produce the interference pattern, but they have to be twins or born in coherence. Antiparticle and particle annihilation does look like two local vibrations cancelling each other, and it may well be the case, but how can we understand this? A pair of antiparticle and particle, say an antineutron and a neutron, is created in an accelerator. It may not be a far fetched speculation to say that these two local vibrations are opposite in phase, off by 180 degrees in time. But we are not talking about this pair of particles that may annihilate each other, annihilation occurs when the antineutron hit anywhere in the accelerator, the walls, molecules in the accelerator, anything that contains neutrons, that is everything. The antineutron will seek out a neutron from the matter, and annihilate it. The particles do not have a grudge against each other. They don’t know each other. They are two independent vibrations travelling in space-time. There is no obvious reason we would expect that they just happened to be vibrating at opposite phase.
This isn’t correct at all. This is confusing particle-antiparticle annihilation with interference, and represents a serious conceptual error. You can see the error as follows; the cancellation you just referred to will not occur for more than an instant. Instead the two waves will pass right through each other. (The equations for waves on a string are nearly linear equations, even accounting for fraction, and they nearly satisfy superposition; there is nowhere near enough interaction to cause the two waves to annihilate into friction-related heat.)
All four forces can participate in annihilation. Among the many, many possible processes, let’s pick four examples:
EM: electron-positron –> two photons
strong: quark-antiquark –> two gluons
weak: electron-positron –> W+ and W-
gravity electron-positron –> two gravitons (extremely rare but certainly possible)
The first three of these have been directly observed.
Although I’m a barely educated casual observer, I’d like to take a stab at TOE in the hope that humans are not their own anti-particle. This wild conjecture is premised upon my own simple geometric imagery that likely only flies in the bastion of my ignorance but… The transmutation of particles and energy described above suggests that all of the particles and energy itself are just different configurations of the same elementary particle, presumably gravitons. The physical particles seen in colliders are the most stable graviton configurations, (think Bucky Balls of different sizes), that garner energy and momentum from attachment of gravitons in the interstitial spaces on the surface of the particle at specific locations to generate vector. Strong, weak and electromagnetic forces may just be the manifestation of graviton interaction when physical particles are excited to specific resonant field orbits that form characteristic force carriers when disrupted in that particular orbital field state. Dark Matter and Dark Energy could be most easily explained as accelerated gravitons emanating from disassociated matter in Super Massive Black Holes that must decay before reaching a lower energy that allows attachment, (absorption cross section), to baryons and photons at some distance from their source dictated by the emission acceleration that is proportional to the size of the SMBH and the galaxy itself, (yields consistent rotational speeds in galaxies of all sizes and disassociated DM fields, (Bullet Cluster, Abel 520) could still have an unseen SMBH source). For some reason, once these accelerated gravitons decay further, (beyond the DM halo and below the photon absorption cross section), they manage to attach to baryons on the opposite side to accelerate that baryon in the direction of initial momentum and manifest as DE, (function of wavelength or gravitons could be initially clustered upon emission from the SMBH to affect absorption characteristics upon further disassociation?). I suspect that down quarks have a larger cross section to the DE gravitons given the hydrogen cloud spanning Abel 399/401, (disproportionate deuterium distribution determined via spectral analysis?) . Too simple? I could speculate about anti-particles, anihilation, BECs, dipole effect, electromagnetism, superconductivity, etc. but I suspect a few choice insights will dispel my imagery at this stage anyway.
Next time you get high try just writting a song
Is there any way that the direct result of anihilation can be a photon of visible light, especially in electron-positron anihilation? Or can such a photon be a result of immediate decays of paticles that are the result of anihilation?
If an electron and positron annihilate, the total amount of energy available (from the point of view of someone who is at rest with respect to the electron-positron pair) is about one billion electron volts. The energy in a photon of visible light is about 2-3 electron volts. So if the electron and positron annihilate to make two and only two photons, the two photons each have hundreds of millions of times too much energy for your eye to detect them. Indeed, such “gamma-ray” photons will do a little genetic damage inside your eye.
However, it is possible for the annihilation to produce 3 photons, or 4, or 10, or 520, etc. The more photons the more unlikely it becomes, but there is a reasonable probability (I haven’t calculated it, but one could) that one or more of these photons might be visible. Most of the energy will still be in invisible photons far too energetic to be visible.
The likelihood that the majority of the energy of the annihilation comes out in a few hundred million visible-light photons is incredibly tiny and has probably never happened in the history of the universe, which has had a LOT of electron-positron annihilations!!!
“but there is a reasonable probability (I haven’t calculated it, but one could) that one or more of these photons might be visible”
So, the photons don’t necessarily have equal energies? What’s special about the 2 photon situation that they have to or is it possible after all that one of them is visible and the other even more energetic gamma ray photon?
By “reasonable probability” do You mean it happened in the lifetime of the universe or that one could see flashes of light while observing some source of positrons?
Two more questions:
I understand that only one photon cannot be created in annihilation because it momentum has to be conserved yet the photon has to move. But what about other bosons that are their own antiparticles? Can a product of highly energetic positron/electron annihilation be only one Higgs boson (for example).
Is it possible that more than one pair annihilates? If we we arrange it so that 4 electrons and 4 positrons meet at the same point in time, do we treat this like one event where the total energy of resulting particles is equal to that of those 4 electrons and 4 positrons or is such a thing impossible according to our theories and in the experiments of this kind no particles were observed with energies greater than in a single annihilation of electron and positron?
The only constraints on the energies of the photons are those of energy and momentum conservation. A single photon is forbidden by those considerations. Two photons are allowed, but they must have equal energy and and opposite momenta in the rest frame of the annihilation. (You might find http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/mass-and-energy/ useful.) Once the number of photons is greater than 2, then the number of constraints is too small, and so the energies can be anything; two could be very high energy and one could be very low. The sum of the energies still has to be the total energy that the annihilation created.
If a particle has a mass M, then the energy required to make it is M c-squared. If you smash an electron and a positron (or two photons or two gluons or other appropriate pairs of particles) together such their their momenta are equal and opposite and their energies are both equal to (1/2) M c-squared, then in principle, as far as energy and momentum are concerned, it may be that the particle of mass M can be created in that annihilation. That doesn’t mean it’s likely. And it may be impossible, because conservation laws of other sorts also have to be obeyed. (The requirement that the particle be its own antiparticle is not a proper requirement; for instance, an electron and an anti-neutrino can make a W- particle in a collision, and the anti-collision, where a positron and neutrino make a W+, is also perfectly allowed.
If you have two electrons and two positrons, the annihilation process occurs pairwise with extremely high probability. First, the pairwise annihilation is intrinsically more likely; fewer electromagnetic interactions are required. Second, it is technically difficult to get four particles into the same location (think about how much harder it is to arrange a meeting with three extremely busy friends rather than just with one). The reverse process — where two photons annihilate to make two electron-positron pairs rather than one, does not suffer from the second problem, though it still suffers from the first. The probability of having a second pair can be as small as 10000 times smaller than just having one pair (though the probability grows slowly as you increase the energy of the annihilating photons.)
Another excellent article. I know that it is possible for a particle can meet and produce an identical particle\antiparticle pair, ‘scattering’ I believe it’s called. I know photons are their own antiparticles, in a sense at least. Two photons can meet and produce particle\antiparticle pair. So is it possible for photons to not interfere but to scatter off each other? Two photons meeting, and producing two photons moving in a different direction? And if so, would their energies have to be equal?
Yes, two photons can scatter — though because they do not interact directly it can only happen through an indirect quantum mechanical effect.
If they meet with equal energy (from your point of view), then — as is true for any two particles of equal mass and equal energy that collide — they will exit the collision (from your point of view) with equal energy.
Thanks for your answer. Though I am still not very clear. When two waves in opposite phase interact the amplitude of the wave becomes zero which according to wave theory means zero energy. Is it not? While according to the theory of conservation of mass and energy the net mass-energy has to remain the same what actually happens in this case?
If you create two waves that are EXACTLY in opposite phase moving in EXACTLY the same direction, you’ve created nothing at all. The amplitude of the wave was zero to start with and it remains so. There’s nothing there.
If you create two waves that for a brief moment are EXACTLY in opposite phase but are moving in opposite directions, then the amplitude of the wave will not be zero most of the time — it will be zero only for a moment, and then it will be large, and then zero again for a moment, and then large — so there is definitely something there, and lots of energy.
I have a doubt. When light waves opposite in phase meet there is destruction of waves. Is this similar to a photon and an antiphoton meeting each other? What happens to the energy when they meet?
No, this is simply interference. A photon can interfere with itself; two photons can interfere with each other. The cancellation is not (indeed cannot be, thanks to energy conservation) perfect; the energy is lost in some places but gained elsewhere. That’s why you get an “interference pattern”, with some dark areas and some very bright areas.
There is no such thing as anti-photons; an anti-photon is just a photon. (All types of particles have anti-particles, but in some cases the anti-particle is the same type of particle as the particle you started with.)
You have written previously on the remarkable complexity of a proton’s structure and this got me to wonder how two newly minted particles – proton and antiproton – with such an intricate structure could appear out of the chaotic mess of two colliding protons.
Question 1
Assuming, for the sake of argument only, the existence of a fourth spatial dimension, is it possible that colliding particles and their corresponding antiparticles unite and disappear into a higher spatial dimension rather than ‘annihilate’ in a burst of energy and cease to exist?
Question 2
In the case of proton to proton collisions above an energy level of about 6 Gev, could a possible explanation of the occasionally observed outcome:
p + p > p + p + p + p bar
be that a joined proton-antiproton pair hidden in the fourth spatial dimension was split apart in the collision and appeared in our 3D space as two separate particles? As far as I can tell, the mass energy equation would remain valid.
Question 3
Finally, could this possibly be the remarkably puny type of Dark Matter particle discovered some years ago by the DAMA group?
If energy is conserved after a collision, then the particles have not annihilated; they have changed.
What does “stationary” particle mean? Holding still? In the same place? Not spinning? Is there such a thing?
Pls explain
“If energy is conserved after a collision, then the particles have not annihilated; they have changed.”
This is semantics. The word “annihilated” was chosen to describe a change in which particles of one type are no longer present and particles of other types emerge instead. For instance: suppose an electron and positron annihilate into three photons, or four, or five. This can happen. Would you still want to call this merely a `change’? Who changed into who?
Stationary, in particle physics: holding as still as possible relative to me (which in quantum mechanics depends on how well I know where it is… remember our friend the uncertainty principle — if you know where something is, precisely, then you don’t know where it is going, and vice versa; but you can know both location and motion at the same time if you accept a certain approximate knowledge of both.) Practically, stationary tends to mean: moving much slower than I can measure. How slow that is depends on context.
Stationary does not mean “not spinning”.
When reading articles like this I can’t help but laugh out loud sometimes when I feel that exhilaration of connection and understanding. This article in particular makes good cement to connect what I’ve learned and read about particle accelerators here. Very well done!
Many thanks for your very interesting article. And a couple of questions:
1. You wrote that the transformation happens “through the action of one of the four known forces.” Could you say a bit more about what actually happens here. I guess there is a lot going on, hence your use of the shoebox. But this is one of the things I comprehend least (the other one is how exactly gluons, photons, etc. mediate forces).
2. Energy and momentum could also be conserved if muon and anti-muon are transformed into a … muon and anti-muon. Is this possible? If no, why not? If yes, does that mean that particles and anti-particles could collide and “nothing” would happen?
3. In order to annihilate, particle and anti-particle must meet. How does that work when I had, say a pen composed of anti-matter (anti-protons, anti-neutrons and positrons) on my table? Would it immediately blow a hole in the earth? Or would it just dissipate away over time?
1. Hard to answer this very well; it lies at the very heart of what interacting fields do. Collisions of ripples in one type of field can generate ripples in another type of field with which they interact. As for how gluon FIELDS and photon FIELDS mediate forces (it isn’t the particles that do this, see my article on why virtual particles shouldn’t be thought of as particles, http://profmattstrassler.com/articles-and-posts/particle-physics-basics/virtual-particles-what-are-they/ ) this is not simple either; you really have to do a calculation to see it, especially to see electromagnetic forces are attractive for opposite charges and repulsive for equal charges. I can throw analogies at you, but they’re wrong.
These are the simplest calculations in quantum field theory, but they do require understanding what quanta are and how they can behave. I’ll keep thinking about whether there is a simple way to approach this.
2. Yes, we call this muon-antimuon scattering. It’s not very different from two tennis balls bouncing off each other — the two outgoing particles move at an angle relative to the incoming ones. So it’s not that *nothing* happens, it’s just that the particle types don’t change.
3. I haven’t calculated it, so here’s a guess: a little part of the pen would meet a little part of the table, explode, and blast the rest of the pen and much of the table to tiny fragments. What happens when the remnants of the pen hit the walls of the room would be additional explosions, I suppose, and this would continue until the pen’s remnants were all microscopic. Ok, now someone needs to go off and calculate whether that’s true.
This is one of the most fundamental questions in the veiled reality concept .
You may read ( on physics and philosophy ) a very good book by a great physicist.
Thank you for your direct answer. Your claim that the probabilistic behavior seems fundamental and not due to a lack of knowledge raises a great question of epistemology: how do you distinguish between ‘no causes’ and ‘hidden causes’ when all you have is ‘no known causes’?
Doesn’t the fact that probabilities are precisely measurable an argument for the existence of determining, hidden factors for each event? How is refuted the hypothesis that the probabilities reflect the combinations of a complex system (ie, made of several hidden variables).
I never found a precise refutation of Einstein’s arguments about the incompleteness of the probabilistic interpretation (I refer to this: http://www.marxists.org/reference/archive/einstein/works/1940s/reply.htm), at least in terms I can understand.
Can you recommend me some links to deepen this question?
Of course the epistemological questions are huge; and physicists have been addressing them (along with some of the more expert philosophers) for decades. Unfortunately, I do not know of any really good and also trustworty explanation for someone who has never learned a little bit of quantum mechanics, and I am certainly not in a position to write one right now; it would be among the most difficult of tasks.
Just to give you a sense of how deep and important the issues are, and that experiments *can* address your questions (but not in ways that I can explain in a short answer), here are a couple of links:
It all starts with Bell (actually with the Einstein-Podolsky-Rosen observation, sometimes called a `paradox’) where he provides answers to your question of how one can test various assumptions about what lies behind quantum mechanics. There’s a summary of this (in a trustworthy place, but I have not myself checked its complete accuracy)
http://plato.stanford.edu/entries/bell-theorem/
Note that recent experiments are quoted as having settled one of the key outstanding issues, in favor of the interpretation that I mentioned. Bell’s original proposal was greatly strengthened by later theorists, as described in this lecture by one of the great physicists of the last fifty years, Sidney Coleman.
http://media.physics.harvard.edu/video/?id=SidneyColeman_QMIYF
However you should by no means consider these subtle issues permanently settled. Discussion and study continues.
In the case of a muon and anti-muon at rest turning into two photons, what exactly is determining the direction of the photons? (or is it some sort of impredictable contigency?)
When exactly the muons annihilate; whether they turn into photons or an electron/positron pair; which direction the photons, or the electron and positron, end up moving; these are all things that, in our quantum world, are (as far as we have ever been able to tell, after 85 years of work) are unpredictable in their details, and can be predicted only probabilistically. There appears to be fundamental randomness in the universe, so that only probabilities can be predicted. For instance I can tell you that if I have some number x of muon-antimuon pairs, where x is very large (say, a million), then I can calculate very precisely that y of them will turn into electron/positron pairs and z of them will turn into photons, and I’ll get that just about right. But given a single muon/anti-muon pair, I cannot tell you what it will actually do, only what the probabilities are for what it may do.
The fundamental probabilistic nature of predictions in quantum mechanics — the loss of determinism (for which the past determines the future precisely) — appears to be not due to a lack of knowledge about the past (i.e. incomplete information) but due to actual probabilistic behavior in the physics (i.e. a real lack of determinism in nature.) This bothered Einstein deeply (as it did many others, and still does.) But years of research trying to understand this, including some very subtle and clever experiments that can actually tell the difference between these possibilities, have only succeeded in supporting the probabilitistic interpretation of the data.
Long story — obviously!
I can understand why an electron-positron annihilation cannot produce a single photon (in the center of mass system, total momentum is zero, so the resulting photon would have zero momentum, which is impossible), but is it possible to produce 3 photons in a single annihilation? What about 4? Or 2321?
Yes, photons are cheap; is possible to produce 3, or 4, or more. I am describing only the simplest (and most common) situation.
The probability to emit a third energetic photon is smaller by about a factor of a hundred. The probability to emit a fourth photon also is smaller by about a hundred. And so on. So we can definitely observe electrons and positrons annihilating to more than two photons, but not many more, because the probabilities for additional emission fall off very fast.
(A subtlety: The probability of emitting a very low-energy photon that you won’t even be able to detect is actually quite high, but since the energy and momentum of such a photon is so low, it doesn’t measurably affect the energies of the two energetic ones, and so it doesn’t affect anything I’ve told you.)
In the case of muon-antimuon annihilation, you can ask whether it is possible to produce more than an electron-positron pair. Again the answer is yes. A single photon, or two photons, or three or more photons, can be added to the final state. And you can even have two electron-positron pairs, or three. [You can’t have something like two electrons and a positron, because that would have non-zero electric charge, and electric charge is conserved.] Again, though, the more particles you add, the less likely the process becomes. So most of the time, you get just an electron and a positron; occasionally you get something more.
The rates for all of these different processes can be calculated in detail, and compared with experiment. That they work to very high accuracy and precision is a powerful test of quantum electrodynamics (the quantum field theory equations that describe the interactions of photons with electrically charged particles.)
Especially concerning “boosted” annihilation reactions (e+e- reactions in colliders, for examples), I always liked the way Bruno Touschek put it: such a reaction “deposits a high density of energy in the vacuum, and lets us see how it likes to resonate”.
I always wondered, could you say that such high concentrations of energy can “take one or more virtual particle(s) in the standard world”? (put them on mass-shell)? In the various courses I followed, I learned that it’s very controversial what degree of “reality” should be assigned to virtual particles. What’s your take on that? Many like to think of them as just terms in second-quantized equations, but when something measurably pushes metal plates together (Casimir effect) and makes LHC collision go boom in a way they couldn’t otherwise (valence-sea and sea-sea quark annihilations), I’d say they are as “real” as lots of other things in physics.
So, why would it be impossible for a relatively motionless e+/e- pair to turn into a muon/anti-muon pair? Can’t we pick a frame of reference where the e+/e- pair is moving with velocity ‘v’? Then, all that would be needed is for the generated muon/anti-muon pair to travel with velocity less than ‘v’? That way, the increased mc^2 rest energy would be balanced by the decreased motion energy? The new velocity, v’, just has to satisfy:
m_e * (c^2 + 1/2*v^2) = m_mu * (c^2 + 1/2*v’^2)
I think, for certain ratios of m_e/m_mu, that would lead to v’ greater than ‘c’, but as far as I can make out, not for all velocities?
But there must be something wrong with my logic, since what holds in the rest-frame of e+/e- should hold in other relative frames too?
Two problems with this. First, in relativity the expression for kinetic energy is m c^2 (1/\sqrt{1-(v/c)^2} – 1). And, second, in your example, momentum will not be conserved.
1) I am aware of the expression you wrote; it is in every textbook. The expression I wrote, and the expression you wrote, are equal. Try it; work out what “v” is using the expression (M-m)c^2, and then plug the result back into your expression.
2) Explain, please, why momentum will not be conserved. In every case I wrote down, the initial total momentum is zero; the final total momentum is zero. [Remember momentum is a *vector*.]
Indeed, your logic is flawed. You’ve only written the equation for conservation of *energy*. You must also conserve
*momentum*; that gives you another equation, and at that point you will find there is no v for which there is a solution.
Thanks for the explanation. I always found the momentum-conservation law rather nonintuitive (I assume many, many experiments over centuries show it to be true, but the only explanation, as opposed to a description, I could find was Noether’s theorem linking it to translational invariance).
PS: Parlyne was responding to my post, not yours.
Prof. Strassler,
What exactly is motion energy? Everything moves with respect to some frame of reference?
So, for the impossibility of electron/positron turning to muon/anti-muon pair:
Even if e-/e+ were stationary w.r.t each other, from a frame moving away, they recede, say at velocity ‘v’. Isn’t it then possible for them to change into a muon/anti-muon pair receding at a slower pace (velocity less than ‘v’), that way conserving energy? Even though the muon/anti-muon pair has higher mass-energy, they have lower motion energy.
Energy of motion is frame-dependent; yet total energy is conserved. This is surprising, tricky, but true. We will see an example of this in my upcoming energy article. Stay tuned.
I assume that the discussion of antimatter as
matter traveling backwards in time refers to
Feynman’s “demonstration” that anti-particles
must exist based on an argument involving the
Fourier integral over positive energies only.
Earlier there was Dirac’s notion of anti-electrons
as holes in a sea of electrons in negative energy
states.
Although you didn’t mentioned the electron hole
view of antimatter you discourage Feynman’s approach.
Is there a current view on trying to “understand”
the relationship between particles and their
corresponding anti-particles?
Yes, I decided to skip the electron-hole argument, just to keep my answer shorter. As you say, another [technical] way to think about a positron is as the absence of an electron. Of course it is at first confusing as to why the absence of an electron has positive energy and not negative energy. And what about the fact that an electron can be thought of as the absence of a positron? Moreover, it is also confusing that the W- particle cannot be thought of as the absence of a W+ particle, even though they are each others’ anti-particles. So…
I would say there really isn’t anything left to be understood about the relationship between particles and anti-particles. Quantum field theory tells you everything you need to know, and has done so convincingly for forty years.
Now it is clear that in the most deep layer of physical reality there are no essences , ONLY RULES , that is really amazing as RULES are extra-physical.
That’s too quick a conclusion, I would say. There are *equations* governing how fields interact with each other. From these equations, rules about particles can sometimes be derived. But the equations predict more than just rules; they give precise numerical predictions for particles’ behavior.
Do you think it’s worth noting why an electron and positron can’t annihilate to form a single photon?
Yes, it’s a good point. I need to do this by expanding this article to include the 2 -> 1 reaction: particle + anti-particle –> new particle.
That seems out of the scope of this article. Though he already mentioned it in the decay articles. Conservation of spin that is.
Is it also possible to transform electrons into muons by adding energy such as collision with x-ray photons?
Looks like a great new series, Matt! At some point you might address the role of “collisions” in the transformation of particles. I understand that in order for a pair of “light-weight” particles to turn into a pair of “heavy weight” particle, they must have sufficient initial motion-energy to supply the missing mass-energy. But why must they collide? If they are moving fast enough, why can’t the transformation take place when the particles are, say, 1 cm apart? I assume it has something to do with the properties of the force that mediates the transformation. But for those of us who follow the LHC experiments, for instance, it often seems like there is something magical about collisions–almost as if the initial particles have to be destroyed in order to make the “dust” from which the final particles are constructed. Can this be right?
You say “mass isn’t conserved”, but isn’t the mass of a thing really just the energy in its rest frame? I.e., if an electron and positron (initially at rest) annihilate to produce two photons, the energy of the photons (in the frame where they have zero total momentum) will be equivalent to the masses of the particles you started with. So maybe the system of photons has a mass, even if the individual photons don’t.
Yes; the mass of the system has not changed; but that’s just a restatement of energy being conserved, along with momentum being conserved.
As you say, the mass of a system containing multiple objects is just its total energy, as viewed from its rest frame (the frame where the total momentum is zero), divided by c^2. And because (a) energy is conserved, and (b) the rest frame of the system does not change during the annihilation process (since no momentum came in from outside), the mass of the system before the annihilation takes place is the same as the mass of the system after the annihilation.
But the mass of a system is not the sum of the masses of its constituents. We’ll get to that in future articles. And that means that the sum of the masses of the constituents is NOT conserved. That’s what I mean when I say that mass is not conserved; you cannot add up the masses of the particles that you have at the beginning and expect them to equal the masses of the particles that you have at the end. The sum can go up, or down.
By contrast, the energy of a system is the sum of the energies of all of its constituents plus all of the energies of the relations between the constituents. And that sum is the same before and after. That point is coming up in a future article.
Thanks for the reply. That makes sense. I’m looking forward to the rest of this series.
Now is it correct to put “field” after every particle name in the article ?
Are fields the realities that are transformed from category to category ? then is motion creates a field ?
No; in this article I am talking about the particles (ripples in the fields), not the fields themselves.
I cannot grasp how MOTION is transformed to MASS?
I know the relation , but this is pure math. , what physical mechanism transform motion to mass ?
You are starting a very precious website , we greatly appreciate what you are doing , thanks again.
aabed with respect
I don’t think I have a good way to answer that other than to say this is what happens in the equations. I’ll think about whether there is a good analogy.
How do you feel about my use of the notion of dissipation to explain why particles decay? http://profmattstrassler.com/articles-and-posts/particle-physics-basics/why-do-particles-decay/most-particles-decay-why/ Because in decay, we start with mass-energy before the decay and end up after the decay with lots of motion-energy. If you become comfortable with this notion in the context of decay, you will then become more comfortable with how this process can work in these particle + anti-particle reactions.
Matt. : You did not tell us a very important point , that is :
What are charges ? what is the physical meaning of charge ? – or + is our definition but what it means ?
Are electric and quark charges some UNKNOWN properties which we can never know ? how charges are materialized from no charge as in case of energetic photons materializing electron-positron pair ? this point is very fundamental to this great article.
thanks
This really has to be addressed in a different article. It may be fundamental, but for the purposes of the current article, I ask you to accept electric charge as a property that particles may have.
As you can tell, I am building a knowledge web, but the web emerges slowly. At any given moment it is incomplete.
Is it still correct/useful to view antimatter as just matter travelling backwards in time?
Oh, I am glad you asked that. I should have a short page about this.
Is it Correct: technically yes. But it’s very much a technical point that the previous generation got way too excited about. It’s really about where certain minus signs go in equations. For those particles such as electrons that are not their own antiparticles, the mathematics governing the evolution of a particle as time moves forwards is the same as the mathematics governing the evolution of an antiparticle as time moves backwards. And the reverse is true; the mathematics governing the evolution of a particle as time moves backwards is the same as the mathematics governing the evolution of an antiparticle as time moves forewards.
Is it Useful? No; I strongly encourage my students not to think this way. There are several reasons.
* If something is meaningful physically (and not just mathematically) there should be some experiment you can do to study it. But asking “which way is the particle moving in time?” is as bad as asking “is the green part of a rainbow moving toward the red part or toward the blue part?” It’s meaningless. If I hand you a particle, can you do an experiment to tell me if it is moving forward in time or if it is moving backward in time? No. There’s no physical meaning to this. All we can do is ask: how does the particle move, change, and act as time moves forwards; how does the particle move, change, and act if we imagine time running backwards.
* What do you do with particles such as photons that are their own anti-particles? Are we to say it is ambiguous whether a photon is moving forward or backward in time? What do we do with this ambiguity? Do some photons move forward and others backward?
* Do electrons move forward in time and positrons (their anti-particles) move backward in time? Or is it the other way round, with electrons moving backward in time and positrons moving forward? Nothing in the equations tells us the answer, and there’s no experiment which could answer the question either. The fact that we call electrons matter and positrons anti-matter is PURE CONVENTION. We could do it the other way round. But what we mean by forward in time is not convention; the universe is expanding, not contracting, as time moves forward.
* There are processes in nature in which a particle and an anti-particle collide to make a … well, a particle, or an anti-particle, depending on your convention. For example, suppose we choose to call electrons and neutrinos “particles”. An electron and an anti-neutrino can combine to form a negatively charged W particle. Suppose we said that electrons travel forward in time and anti-neutrinos travel backward in time. Which direction in time does a negatively charged W particle move? Its anti-particle is a positively charged W particle; it moves the other way. But you make these positively charged W particles from a neutrino and a positron, one of which (if you insist on this way of thinking) moves forward in time and the other backward. In fact, there are many conundrums like this, where two objects come together to make a third; if you try to assign forwardness in time to some and backwardness in time to others, you end up with inconsistencies.
Ugh! Don’t do things this way; it adds nothing to the physics and gets you confused about the mathematics and the concepts. A much simpler, more consistent, and experimentally grounded approach is the following:
– treat all particles the same (moving, changing, acting according to the basic equations as time universally moves forward);
– don’t divide the particles of nature into those that are particles and those that are anti-particles; you wouldn’t know what to do with the photon or the Z particle or anything else that is its own anti-particle
– instead, identify some particles as each other’s anti-particles (in other words, say that electrons and positrons are each others’ anti-particles, without deciding that an electron is a “particle” and a positron is an “anti-particle” — notice this avoids us having to decide whether photons are “particles” or “anti-particles”, since we just say that photons are their own anti-particles)
– note the little mathematical fact that in the equations a particle with normal time evolution looks just like an anti-particle with backward time evolution, but note also that this is not very important in calculations and conceptually does not add anything to our understanding of the physics.
Folks like Feynman popularized the notion of antiparticles as being particles that travel backward in time. But there really is something useful about thinking in this way in a very limited sense: It explains the necessity of including antiparticles in your relativistic quantum theory.
The idea is that particles, by the uncertainty principle, can occasionally (but spontaneously) jump outside their forward light cones (you can see this exponentially-suppressed “tunneling” phenomenon by a calculation from Peskin and Schroeder’s Ch. 2), and therefore will be seen by certain Lorentz observers as going backward in time — i.e., appear as the corresponding antiparticle going forward in time. Not all antiparticles arise in this way, of course, but once antiparticles kick their way into your theory by the light-cone-leaking argument, you have to include them as valid states in your theory. (Weinberg has a nice version of this argument in Ch. 4 of Gravitation and Cosmology — generalizing the argument also leads to the necessity of allowing for multiple indistinguishable particles, as Feynman discusses in his 1986 Dirac Memorial Lectures, and gives the spin-statistics theorem and the CPT theorem.)
One can even make these heuristic semiclassical arguments rigorous by working in the first-quantized worldline formalism for relativistic quantum mechanics — see, for example, the opening chapter of Polchinski’s String Theory, Volume I, or Polyakov’s treatment of relativistic Dirac fermions in Gauge Theories and Strings. The path integral you get contains both the particle and its antiparticle, and the antiparticle corresponds to wordline paths parameterized by proper time that go backward in coordinate time. That’s why you get the correct relativistic propagator in both first-quantized RQM (and string theory) even without explicitly putting an antiparticle (or “antistring”) into your one-particle Hilbert space — it’s secretly there the whole time.
One easy way to see this at the level of the Hilbert space is to note that the path integral gives the constraint (p^2-m^2)|state>=0, but that doesn’t kill off the “negative p^0” states. But because the sign of p^0 is Lorentz invariant for particles with non-negative mass, we can freely redefine the negative p^0 states as positive energy states of the CPT-conjugate antiparticle.
So, to summarize, thinking of all antiparticles as backwards-time particles = not useful, thinking of occasional antiparticles as backwards-time particles = very useful.
I basically agree with you. The link between relativity, quantum mechanics and anti-particles is not something I generally talk about to non-experts, but it might be worth doing. And certainly this does come up in quantum field theory class.
I love physics. The way in which I think I understand something then later realize I don’t understand it at all.
So for each pair of particles it is arbitrary how to assign particle or anti-particle ( and some like the photon don’t come in pairs ).
However, when I read about baryogenesis it seems nature has through some unknown law of physics done precisely that, and put all particles into either the particle or anti-particle bucket.
Right, that is the impression you would easily get if you don’t read very, very carefully… because unlike “particle” and “anti-particle”, the terms “matter” versus “anti-matter” DO have a preferred convention.
The statement that “there is more matter than anti-matter in the universe” is meaningful if we define matter (as we have in common usage for centuries) as the stuff that *WE* are made from: electrons and protons and neutrons.
That is not the same as saying “there are more particles than anti-particles in the universe”, which would not make any sense, because there’s no sense in which electrons must be called “particles” and positrons must be called “anti-particles.”
Of course this is up to us; we could chose to always call electrons “particles” if we wanted to. (And in some contexts it is temporarily useful to do that.) But doing so obscures the symmetry of the mathematics, and, as I described, leads to logical inconsistencies if we try to make this distinction across all the particles of nature.
If we and the earth and the sun had been made entirely from gluons, all of which are their own anti-particles, then what we would in that case have called `matter’ would have had no anti-matter counterpart. We would still have talked about anti-particles — the universe would still have electrons and positrons in it — but what we call `matter’ would have been a different thing, and there would have been no separate stuff to call `anti-matter’.
However, it happens that we are made from particles which DO have distinct anti-particles. And that means that anti-matter is distinct from matter. At that point we can notice that our universe seems to have very little anti-matter in it — hence the puzzle — how is it that in the early universe a tiny asymmetry of matter over anti-matter was created, leading today to our universe with a tiny bit of matter and almost no anti-matter? This is the puzzle that theories of baryogenesis attempt to solve.
I should add that it is not so easy to imagine a habitable universe where anti-matter is not distinct from matter, because in such a universe matter might be able to annihilate with itself, with the consequence that macroscopic chunks of matter (i.e. planets and humans) might be unstable. The universe as a whole would be fine, but we wouldn’t be here.
The differentation between matter and anti-matter is obvious from the historical point but would it not be more elegant to group positive paricles: positron, up, antidown, et al. together and a negative group with electron, antiup and down – sure it does not answer where the antimatter is, but at least it would let our world appear more symmetrical made out of equal amounts “+ stuff” and “- stuff” which are obviously intrinsically stable and therefore make other regions in the universe with somewhat different but equally symmetrical and therefore stable compositions of “stuff” more acceptable?
You could do that, but I’m not sure what it buys you. We already have the three categories of positively charged particles, negatively charged particles, and neutral particles; is your thought to take the neutral particles and divide them in two to reduce the number of categories from three to two? Where will you put photons? How about neutrons and anti-neutrons?
A top quark (charge +2/3 that of a proton) can decay to a W particle of charge +1 and a bottom quark of charge -1/3. So you still end up with particles in one category decaying to particles in both categories.
You could try to divide things by whether they are up-quark-like with respect to the weak nuclear force (which would include up-type quarks, protons and neutrinos) or down-quark-like (which would include down-type quarks, neutrons and electrons.) But then you end up with other troubles down the road, including ambiguity for photons, gluons, Z and Higgs particles, and issues with the decay of top quarks that I mentioned above.
The reason we use the term “matter” is because it does organize particles according to a different categorization than any of these. Unfortunately, as I’ll mention in a different article, the word “matter” actually stands for (at least) three different categories, used in three different contexts. This is obviously confusing for the non-expert!
Agreed it does not change anything other than the way we think of the two categories of matter (here) and anti-matter (missing) – if you change your point of view and consider the universe was created with eaqual amounts of “stuff” and “antistuff” and ideally if a “stuff” particle encounters its exact opposite “antistuff” antiparticle they annihilate (positron- electron) but fortunately for us if it encounters other “antistuff” which is not its antiparticle it creates stable compounds which are more or less durable and therefore the universe persists and has not annihilated itself moments after its creation
well, but again — where do you put neutrons (and anti-neutrons) in this categorization? electrons find protons, but the neutrons are essential too in allowing for more complex elements…
But neutrons are not elementary and in that sense are a (arguably not so stable) composite of “stuff” (up) and “antistuff” (down)
neutrinos are indeed much trickier but possibly do not fall under stuff at all: have minute if any mass, moving at or close to speed of light, have spin but only “onehanded” and sometimes called polaristion (is that misleading and different to the one of a photon?) and even on your diagram of the SM seem to lie somewhere between fermions and bosoms – for a layperson these seem to fit the role for force carrier particles between Ws and leptons (analogy to photoeffect of the atom)
If the neutron is not stuff, then is a proton stuff, or not?
Let’s take helium. The helium nucleus has equal numbers of up quarks and down quarks. Is that nucleus stuff or anti-stuff, or not either?
And you can’t disregard neutrinos; electrons can be converted to neutrinos by the weak nuclear force, and this happens all the time inside the sun’s furnace. (They are fermions, by the way; no ambiguity there. And they are not force-carriers, for reasons which aren’t obvious without more discussion.)
Sorry did not seem to properly explain what I mean: the characteristic of “Stuff” would apply only to elementary particles and therefore protons, neutrons, atoms etc would represent stable combinations of stuff with antistuff:
For example Hydrogen consists of “Stuff” = 2 up quarks and “antistuff” = 1 down and 1 electron
Helium: “Stuff” = 6 up quarks and “antistuff” = 6 down and 2 electrons
anyway was just an idea but seems to complicate things more so lets leave it
Electrons converted to neutrinos in the sun – is that reverse beta decay?
I just noticed I changed from “+ stuff” (all positive elementary particles) to “stuff” and from “- stuff” ( all negative elementary particles) to “anti-stuff” maybe thats where the misunderstanding lies
Does this mean we could look at the anihalation of particles in reverse to figure out how they could be created though?
I would like to think that way too, particles move forward to future and antiparticles move backward to past, and I still would like to keep an open mind about it. But I don’t think that is the case for an antiparticle. Future and past are referenced to the space- time, a frame regarding where the particle is. However, according to the Uncertainty Principle, we can’t be certain about where the particle is at a particular event (coordinates in space time), so we use a local wave function to represent a particle. At a specific point in space, the wave function can be reduced to a local vibration, a periodic motion in time. This is the second time variable involved in the antiparticle and particle annihilation. The first one just tells where the annihilation event occurs in space time, the second one tells how the two particles oscillate in that event. It is a safe assumption that an antiparticle and a particle oscillate in the same frequency as they have the same mass. In this case, the second time variable is reduced to the phase angles of the oscillations. It seems also a reasonable assumption that, when a pair of antiparticle and particle are created, they are created out of phase. If the particles in this pair went different paths and then later brought together in the same point in space, we would expect them to annihilate each other, as they were born that way, they always oscillate out of phase in time. But this is not what we normally see in experiments. We normally see the antiparticle created in the pair production strays away and annihilates the first particle it runs into. The antiparticle and particle in annihilation are total strangers. That is very difficult to understand. We don’t expect two independent oscillations always cancel each other.
I would like to propose a possible explanation about the annihilation with two assumptions. 1) It is not objective to think that we can assign an exact event (a set of coordinates in space time) to a body in motion. 2) The first assumption is equivalent to the Uncertainty Principle. We can justify the first assumption using the General Relativity. In General Relativity, space-time is no longer subjective but objective. Gravity is space-time. If space-time can be curved by the presence of matters, it can also vibrate. If we accept the first assumption, it is easier to agree with the second assumption. To say the motion of a particle is uncertain relative to a fix point in space-time is equivalent as to say the motion of a particle is uncertain because the reference point is uncertain. Based on the second assumption, the local vibration of all the matters (not the antimatters) are in synch with the local vibration of the gravity field, because they are the same motion just been viewed differently. When an antiparticle is created at a point in space-time, it’s vibration is always out of phase with the local vibration of the gravity field at that point no matter where that point in space-time is, and it carries this phase difference moving around in space-time. If a particle always oscillates in phase with the local oscillation of the gravity field at any point in space-time, and an antiparticle always oscillates out of phase with the local oscillation of the gravity field at any point in space-time, they will annihilate each other when they meet at any point in space-time.
I’m sorry, but this doesn’t make any sense. Particle-antiparticle annihilation and creation have nothing to do with gravity. A world without gravity but with electrons and positrons would still have particle-antiparticle annihilation.
Yun Chen Your theory is interesting, it suggests that space-time itself is intrinsically defined by the “particles”/and or/”anti-particles” (field vibrations) within it.
We usually think of fields as “labeled” by space-time, but your idea seems to suggest that fields and space-time are two complementary aspects of the same “reality” (observable Universe).
Quantum gravity is projecting mass, so antimatter must be a reflection. They annihilate. This happened in the big bang and when there is an overload of quantum gravity. Of course energy is produced, which may be fragments left of the collision. As far as a collider is concerned, no one knows what is really taken place: just the remains.
the particles and antiparticle does emerge the spacetime geometry,that already exist through the primary metrics of deformed spacetime,then the antiparticles are reflections of particles and fields,but the antimatter does not exist.for for that reason,the universe exist,and the spacetime is also measured as discretes,quantum and the deformation of spacetime,is the principle,continuum
RONALD POKATILOFF How can quantum charges and symmetries be added to the idea of “mass projection”? The answer to this, I think, could be the solution of the unification of the 4 fundamental forces in QFT.
Yun Chen The following article explores the different connections of matter and antimatter with gravity – possibly related to what you said.
I wonder how gravity waves and CPT invariance could be connected. Perhaps by using CPT as a verified experimental assumption over the geometrical description of general relativity.
“CPT symmetry and antimatter gravity in general relativity” M. Villata (Mar 2011)
“The gravitational behavior of antimatter is still unknown. While we may be confident that antimatter is self-attractive, the interaction between matter and antimatter might be either attractive or repulsive…”
https://arxiv.org/abs/1103.4937
Thanks MATT. , we needed this project very very much.