MATT STRASSLER
Of Particular Significance

Mass and Energy

Matt Strassler [March 27, 2012]

A number of puzzling features of the world — including a number that my readers have asked about in comments — have everything to do with the nature of mass and energy (and also momentum.)  We’ve all heard these words and many of us have a vague idea of what they mean. Of course the notions of “mass” and “energy” exist in English (and in other languages) with multiple definitions. Unfortunately, none of these definitions matches what physicists mean. So you have to leave those other definitions at the door and try to deal with these notions in the precise way that physicists do. Otherwise you’ll end up very confused.

Even before I start, there’s the potential for confusion. In bringing up “mass and energy”, I do not mean to call to your mind a different pairing of words: “matter and energy”, which you will often hear people refer to as though they are opposites, or partners, or mutually exclusive categories, or something meaningful in some other way as a two-some. Well, they’re not. Matter and energy don’t belong to the same categories; putting them together is like referring to apples and orangutans, or to heaven and earthworms, or to birds and beach balls.  [Here’s an article going into more detail about why matter and energy are a false dichotomy.]  Matter (no matter how you define it — and there are different definitions in different contexts) is a class of objects that you will find in the universe, while mass and energy are not objects; they are properties that every object in the universe can have. Mass and energy are in deep interplay, and they deserve to be discussed together. 

To understand mass and energy, we need to put momentum into the mix, and discuss the differences and relations among these quantities.

Energy

The word “energy” appears in English with many different meanings. When we are ill, we speak of feeling as though we have no energy, meaning strength and motivation; we speak of someone as showing lots of energy, meaning high activity; we complain about the rising price of energy, meaning fuel; we speak of spiritual energy as something unmeasurable but profound, perhaps a form of charisma.  All of the various definitions are loosely related, which is why we choose the same word in describing these concepts.   But in physics, energy is none of these things. You’d be making a big physics error if you mix and match one of the English definitions with the physics definition! Within physics, you must stick with the physics term, or you’ll get wrong answers and end up very confused.

Unfortunately, the meaning of “energy” in physics is very difficult to put into the form of a dictionary definition, with a short phrase that characterizes what it is. But do not be misled! This is a failure of language, and does not mean that physicists’ notion of energy is vague. Not at all! In any given physical system, it is very clear what the energy of the system is, both in terms of how to measure it experimentally and (if there are equations that can predict the system’s behavior) how to calculate it.

Part of what makes energy complicated to describe is that it can take many forms, not all of which are conceptually simple.  Here are the three most commonly encountered:

  • First, energy can be locked away in an object’s mass; on this website I call this mass-energy (which is the famous E=mc2 energy associated with mass, and also called “rest-energy”, since it is the energy that an object has when it is at rest, i.e. not moving.)
  • Second, energy is associated with the motion of an object.  On this website I call this motion-energy, whose technical name is “kinetic energy”; this kind of energy is rather intuitive, in that faster objects have more energy than slower ones, which is more or less what we would colloquially expect.  Also, a heavier object has more motion-energy than a light one, if the two are traveling at the same speed.
  • Third, and most confusing, energy can be stored in the relationships among objects (and is typically called “potential energy”). It can be stored in a stretched spring, or in the water behind a dam, or in the gravitational interaction of the earth with the sun, or in the relationship among atoms in a molecule. In fact there are lots and lots of ways to store energy. This sounds very vague, but again, it’s just a failure of words; in every one of these cases, there are precise formulas for what the stored energy of system is, and there are clear and well-defined ways to measure it.

There’s one more thing about this third kind of energy, interaction-energy as I will call it, that is especially confusing at first.  Unlike mass-energy and motion-energy, which are always greater than or equal to zero, interaction-energy can be either positive or negative (and often is negative in interesting situations).   I’m not going to deal just yet with this fascinating and subtle issue.  We’ll get back to it later.  [In a previous version of this article I called this `relationship-energy’, but decided against this choice more recently.]

Energy is a very special quantity, of great importance in physics.  The reason it is so essential [along with momentum, see below] is that it is “conserved” — read this as physics-language for preserved, or for maintained without change.  What precisely does this mean?

If you start with an object or collection of objects — let’s call it a “system of objects” — that has a certain amount of energy at this moment (make sure you count all of it though — all the mass-energy, all the motion-energy, the stored energy of all types, etc.), and the parts of the system interact with each other but with nothing else, then at the end of the day the amount of energy those objects will have is the same as the amount they have now.  Total energy is conserved — the total amount does not change. It can change from one form to another, but if you keep track of all the forms, you’ll find at the end just what you had at the start.

This is true even if some of the objects disappear and others take their place, as will happen if, say, one particle in the system decays to two other particles, which then join the system.

[Just to warn you, in Einstein’s theory of gravity this can get a little hairy; the statement is still basically true, but when you try to keep track of energy over long distances it can become more subtle.  Don’t worry about this now, but someday you may need to know it, so that’s why I mention it.]

Why is energy conserved? Because of a mathematical principle that relates the apparent fact that the laws of nature do not change with time  to  the existence of a conserved quantity in nature, which by definition we call `energy’.

The most famous and general statement of this principle is due to Emmy Noether, one of the great mathematical physicists of the last century and a contemporary of Einstein’s.  (Just yesterday there was a nice article about Noether in the New York Times, perhaps the first time her name had appeared in the paper since Einstein’s moving tribute to her following her untimely death.) Though highly respected among some members of the physics and mathematics communities, she suffered both gender and ethnic discrimination in her home country of Germany (where attempts by mathematics colleagues to get her a professorship at Goettingen were blocked, and from which she fled when the Nazis came to power).  Then, after less than two years in the United States, where she taught at Bryn Mawr (a famous college, near Philadelphia, that even today admits only women among its students), she died of an illness in middle age.

Noether’s famous theorem (actually they are two closely related theorems) tells us that whenever there is a symmetry of the laws of nature — in this case, that the laws of nature are the same at all times — then as a direct consequence there is a conserved quantity in nature — in this case, energy.

Even better, the theorem tells us precisely what that quantity is — what all the different forms of energy are, for a given system of objects, that have to be added up to give the total energy. (Actually methods for doing this predate Noether, but her theorem brings many concepts together in one place.)  This is why physicists always know precisely what energy is, and why it is easier to obtain it through equations than to define it through words.

Momentum

The situation with momentum is similar to that of energy. The laws of nature are the same in all places; crudely speaking, experiments [when properly defined and controlled] give the same answers whether you do them to the north or south of here, the east or west of here, or whether you do them at the top of a building or deep in a mine. Pick any direction in space; then, according to Noether, momentum along that direction is conserved. And since there are three dimensions of space, with three independent directions you could go, there are three independent conservation laws. You can pick whichever three directions you like, as long as they are different. For instance, you can choose the three conservation laws to be momentum in a north-south direction, momentum in an east-west direction, and momentum in an up-down direction. Or you can pick three others, such as toward-and-away from the sun, along-and-opposite the earth’s orbit, and up-and-down out of the plane of the solar system.  Your choice doesn’t matter; momentum along any direction is conserved.

The most common form of momentum is just that due to simple motion of objects, and it’s more or less what you might think intuitively: if an object is moving in a certain direction, then it has momentum in that direction, and the faster it moves, the more momentum it has.  And a heavy object has more momentum than a light object if the two are traveling at the same speed.

One interesting consequence of the conservation of momentum is that if you have a system of objects sitting stationary in front of you (that is, the system as a whole isn’t moving, if you average appropriately over the motions of all its constituent objects) then it will continue to remain stationary unless something from outside the system pushes on it. The reason is that if it is stationary its total momentum is zero, and since momentum is conserved, it will remain zero forever, as long as nothing from outside the system affects it. This fact is going to very important later, so keep it in mind.

Mass, and its Relation to Energy and Momentum 

Now it’s time to turn to mass.

Unfortunately, there is a lot of confusion about mass, because shortly after Einstein’s work on relativity there were two notions of mass that coexisted for a time. Only one (the one which Einstein himself settled on, and which was sometimes called “invariant mass” or “rest mass” to distinguish it from the now-archaic term “relativistic mass”) is still used in particle physics today. I’ve explained this more carefully in a separate article.

Fig. 1: For an object moving according to Einstein’s relativity, the relation between energy, momentum (times the universal speed limit c) and mass (times c squared) is analogous to the Pythagorean relationship between the hypotenuse of a right-angle triangle and its two sides. The velocity of the particle, divided by c, is the ratio of the length of the horizontal line to the length of the hypotenuse; this is also the sine of the angle marked alpha.

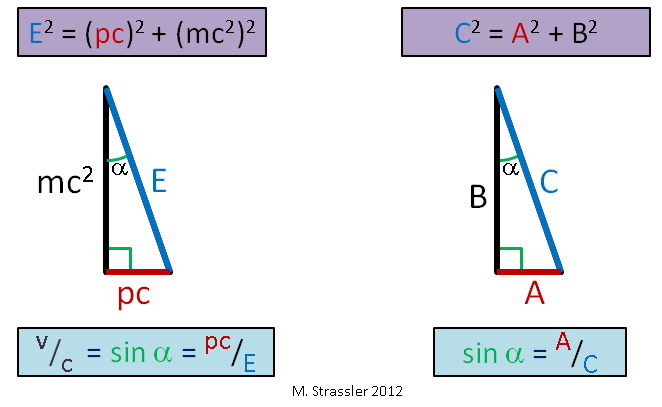
The definition of mass m that I will be using throughout this website is the one that has a particular relation between energy and momentum. For an object that is moving on its own (that is, not interacting in any significant way with other objects), Einstein proposed (and countless experiments confirm) that its energy E, momentum p and mass m satisfy a simple Pythagorean relation

  • E2 = (p c)2 + (mc2)2                   (equation #1)

[Remember Pythagoras, who said that a right-angle triangle with sides of length A and B and hypotenuse of length C has to satisfy C2 = A2 + B2? It’s the same type of relation: see Figure 1.] Here c is a constant speed that, as we will see in a moment, is the universal speed limit. We’ll also see in a minute why it is called “the speed of light.”

According to Einstein’s equations, the velocity of an object, divided by the speed limit c, is just the ratio of p c to E,

  • v/c = (p c) / E        (equation #2)

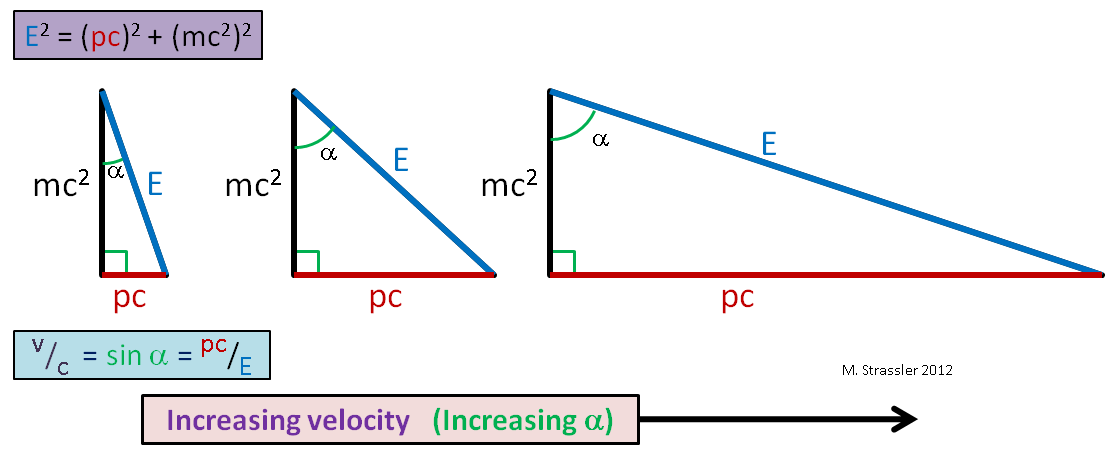
i.e. the ratio of the length of the horizontal side of our triangle to the length of its hypotenuse. (This ratio is also equal to the sine of the angle α shown in Figure 1.)  Wow!  There it is, folks.  Since the sides of a right-angle triangle are always shorter than its hypotenuse (i.e. the sine of any angle is always less than or equal to 1), no object’s velocity can be faster than c, the universal speed limit. As the velocity of the object increases (for fixed mass), both p and E become very large (Figure 2), but E is always bigger than p c, and so v is always less than c!

Fig. 2: As an object is made to move faster and faster, E and pc become larger and larger, and more and more similar in length, while m c-squared remains the same.

Next, notice that if the object is not moving, so that its momentum p is zero, then the relation in equation #1 simplifies to

  • E2 = (mc2)2 , or in other words E=mc2 ,

Einstein’s famous relation that mass is associated with a fixed amount of energy (which is what I call mass-energy on this website) is just the statement that when the triangle becomes a vertical line, as in Figure 3 (left), its hypotenuse becomes the same length as its vertical side. But let me say that again, because it is so important: this relation E=mc2 does not mean that energy is always equal to mass times c2; only for an object that is not moving (and therefore has zero momentum) is this true.

Fig. 3: Lessons from extreme triangles. (Left) A massive object that is not moving has E = m c-squared. (Right) A massless particle must have E = pc, and therefore v = c.

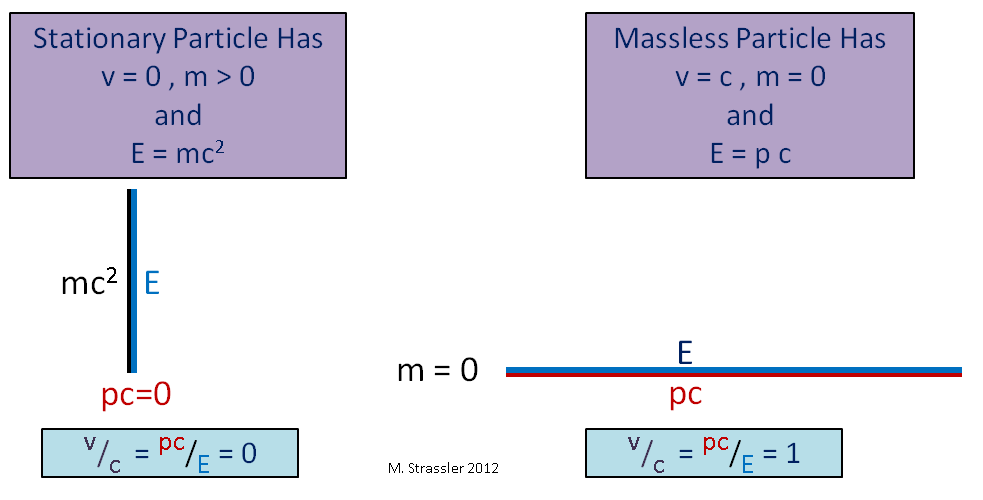
Another interesting thing to note is that for a massless particle, the vertical side of the triangle is zero and the hypotenuse and horizontal side have the same length, as in Figure 3 (right).  In such a case, E is inevitably equal to pc, which in turn means that v/c = 1, or in other words, v=c .  Thus we see that a massless particle (such as a photon [a particle of light]) inevitably travels at the speed c. And so the speed of light is the same as the universal speed limit, c.

Meanwhile, for a massive particle, as shown in Figure 4, no matter how big you make the momentum and the energy, E is always a little bit bigger than p c, and so the velocity is always less than c. Massless particles must travel at the speed limit; massive particles must travel below it.

Fig. 4: Any right-angle triangle for which the vertical side has finite length always has a hypotenuse longer than its horizontal side, no matter how long the hypotenuse becomes; similarly, a massive object’s velocity can never exceed c, no matter how large its energy E is.  (Here “>>” means “much greater than”.)

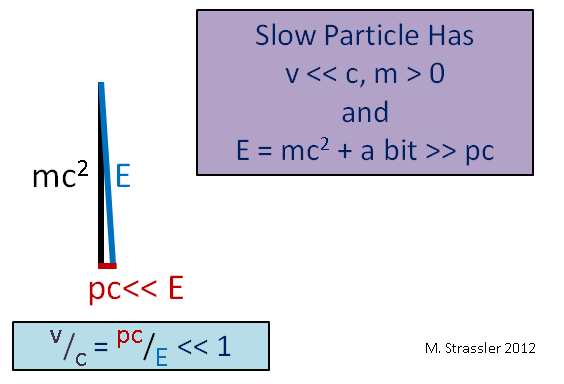
At the other extreme, consider a slow massive object,  moving very slowly compared to the speed of light, as in the case of a car.  Then since its velocity v is much less than c, its momentum p times c is much less than E, and (as you can see from Figure 5) E is just a little bit bigger than m c2.  Thus a slow object’s motion-energy E – mc2 is much smaller than its mass-energy mc2, while a fast object’s motion-energy can be made arbitrarily large, as we saw in Figure 4.

One tricky point I should mention: momentum is not just a number, it is a “vector”. That is, it has a size and a direction; it points in the direction the particle is moving. When I write “p” I’m just referring to its size. In many cases we have to keep track of the direction of the momentum too, but we don’t have to in equation #1 that relates momentum to energy and mass.

Fig. 5: An object moving much slower than the speed of light has momentum (times c) much less than its energy, and has just a little bit of motion-energy compared to its mass-energy.  (Here “>>” and “<<” mean “much greater than” and “much less than”.)

A final tricky point: I’ve used triangles and a bit of ordinary trigonometry because everyone knows them from high school.  But experts-to-be should beware: the right way to understand Einstein’s equations is using hyperbolic trigonometry, which most laypeople never encounter, but which is essential for understanding the structure of the theory, and makes important details such as how two velocities add, why lengths contract, etc., far more transparent.  Non-experts can safely ignore this, though someday I might write a page explaining it, as it involves lovely mathematics.

But Velocity is Relative…?

Now if you’ve been paying attention, you’re wondering what the heck I’m talking about. You know that the speed of a particle — or of anything that travels slower than the speed of light itself — depends on your point of view.

If you’re sitting at home reading a book, you would claim the book has zero velocity (and relative to you, it is indeed stationary) and therefore it has no momentum and no motion-energy, only mass-energy. But if I were standing on the moon, I would remind you that the earth is spinning, so you’re actually being carried along by that spin, and moving (relative to me), at hundreds of miles (or kilometers, if you prefer) per hour. So you, and your book, do have momentum, according to me.

Who is right?

Galileo’s version of relativity — the first relativity principle — argues that you and I are both right. Einstein’s version of relativity agrees with Galileo on this point — that both you and I are correct — but makes important adjustments to what followers of Galileo’s relativity would have claimed for the energy and momentum and mass of the book, by setting them into the Pythagorean relationship of equation #1.

But if everyone is right, which E and which p should I put into the energy/momentum/mass relationship, E2 = (p c)2 + (mc2)2 ,  our equation #1, for the book? Should I put the E and p that you measure as you read the book, namely E = mc2 and p=0? Or should I put the E and p that I think the book has, watching you move with the earth?

The answer is the whole point of Einstein’s equation #1. Every observer will measure a different E and a different p for the book, depending on how fast the book is moving relative to them; but for every one of these observers, the equation E2 = (p c)2 + (mc2)2 will be correct!!!

Magic! Actually no, just genius — the recognition in 1905 of how to replace the set of relations proposed by Newton and his descendants with a profound new set of relations which were still consistent with earlier experiments but do turn out to be a more accurate representation of reality. You can’t fully appreciate how much of a mind-bend this requires until you look at all of the ways that this could have gone wrong, and how many other equations you could have proposed (and some people did) for which inconsistencies internal to the mathematics, or disagreements with previous experiments, can arise. (Indeed, amateur physicists send me their attempts to “correct” Einstein’s equations all the time, but I’ve never seen any of them thoroughly check whether their own equations are fully self-consistent… a very tall order, and the downfall of most theoretical ideas.)

But then, How can Energy and Momentum Be Conserved?

Now wait! you say, with your head about to split open and brains about to spill onto the floor [and yes, I do remember how this feels] — energy and momentum are supposed to be conserved — so how can different observers disagree about what they are?

More magic — actually predating Einstein. Trust me, the universe is a very, very clever bookkeeper, and even though different observers will disagree about how much energy an object has, or a system of objects has, they will all agree that this energy does not change with time. The same is true for momentum.  I promise we’ll see examples of this later.

Mass, however, is completely different from energy and momentum. First, unlike energy and momentum, mass is simply not conserved. There are all sorts of processes in nature in which the total mass of the objects in a system change; for instance, a massive Higgs particle (if such things exist, and they probably do) can decay into two massless photons. There’s no symmetry associated with mass, and Noether provides us with no conservation law.  But second, as I mentioned before, unlike the energy and momentum of an object (or system of objects), whose values depend on the observer (in particular on his or her speed relative to what he or she is measuring), all observers, no matter what they are doing, will agree on the mass m of an object (or system of objects).   This is not obvious at all; it is true because of the devilishly clever way that Einstein’s equations work.

Where We Are So Far

So — now you know a bunch of perhaps seemingly conflicting things. You know

  • Energy and momentum of an isolated physical system are conserved (the total energy and the total momentum of an isolated system doesn’t change over time) from every observer’s point of view
  • But different observers, if they are moving relative to one another, will assign a different amount of energy and momentum to the system!
  • The sum of the masses of the objects that make up a physical system is not conserved; it may change.
  • But the mass of any object is something that all observers will agree on.

To this list of facts we will add two additional facts and two conclusions:

  • The mass of a physical system of objects is not the sum of the masses of the objects that make up that system.

Instead, the mass of a physical system, which all observers agree on, is determined by its energy and momentum, and satisfies its own version of equation #1:

  • (Esystem)2 = (psystem c)2 + (msystemc2)2                   (equation #1′) 

It follows then, without the need for an additional conservation law, that even though the sum of the masses of the objects that make up a system is not conserved, the mass of the system is conserved, because it is related by equation #1′ for a system to the energy and momentum of the system, which are conserved.

In fact,

  • the mass of a system of objects is the only thing on our list that is both conserved and agreed by all observers.  

We just have to remember that the mass of a system is not the sum of the masses of the objects that make up that system, but something given by equation #1′.

Rather than my trying to explain this any further, let’s see how it works. An illustrative example is worth a thousand words. And I’m going to use the most current and famous example of them all: let us take, as our system, a Higgs particle (which I’ll assume to have mass of 126 GeV/c2), and see how the various statements made above play out when the Higgs particle decays to two photons.

One Higgs Particle, Two Photons, and Three Observers

Fig. 6: Our three observers looking at a Higgs particle; with respect to the Higgs particle, Peter is stationary, Marie is moving down, and Chris is moving to the left.

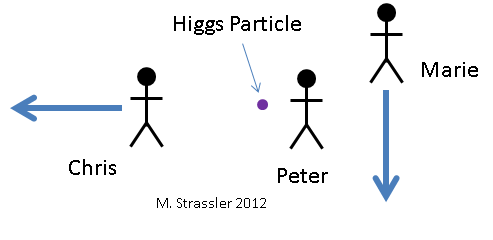
So what we’re going to do is look at a Higgs particle decaying to two photons from the point of view of three different observers.  These observers are shown in Figure 6, along with the Higgs particle that they are initially looking at.  (Not that they can actually “look” at it with their eyes; it’s around for far too short a time, and is far too small, to see.  It is their scientific instruments that will give them some opportunity to understand its properties.)  One, whom we’ll call Peter, views the Higgs particle as not moving at all. Marie is moving down, relative to Peter. And Chris is moving to the left, relative to Peter. That means Marie sees the Higgs particle as moving up, while Chris sees it as moving to the right. How these three observers see the Higgs decay is sketched in Figure 7. Peter sees the Higgs decay to two photons of equal energy, one going up and one going down. Marie will see the Higgs decay to two photons of different energy, the upward-heading one with more energy than the downward-heading one. And Chris will see the Higgs decay to two photons that are heading up to the right and down to the right. What we’ll do next is figure out (a) what energies and momenta does each of these observers assign to the Higgs and two photons? and (b) how does each of these observers come to the conclusion, separately, that energy and momentum is conserved in this process?

Fig. 7: Peter sees the Higgs stationary, then sees it decay to two photons of equal energy, moving upward and downward. Marie sees the Higgs moving upward from her point of view, and then sees it decay to two photons of unequal energy (the upward-going one having the most energy). Chris sees the Higgs going to the right and decaying to two photons that have equal energy but move diagonally up and down and to the right. In Figures 8-10 we’ll see what energies and momenta they assign to all the particles.

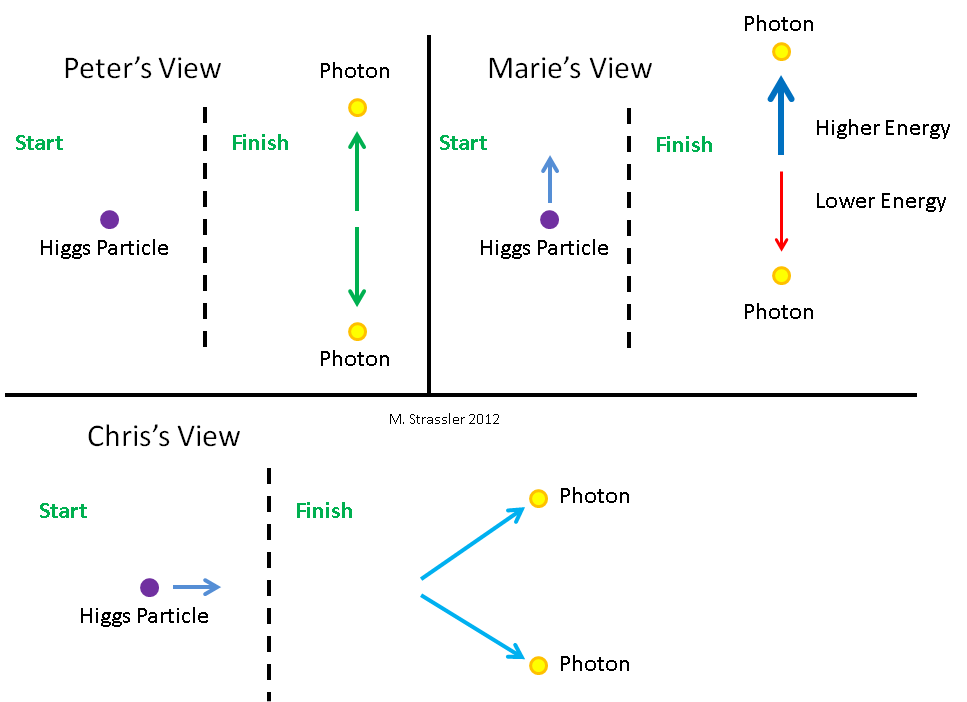
A Stationary Higgs Particle Decays

Let’s first examine the Higgs particle from Peter’s point of view. Peter stares (or rather his measuring apparatus “stares”) at the Higgs, and sees what? (I’m going to put a bar over everything that Peter observes; we’ll compare this with what Marie and Chris observe later.) The Higgs isn’t moving, so its momentum p0 is zero, and by Einstein’s equation #1 the Higgs, with its mass of m = 126 GeV/c2, has energy E0 = m c2 = 126 GeV.

Now according to the conservation of energy and momentum, the system of a Higgs particle will retain all of its energy and momentum as it decays. (This is true as long as nothing external affects the Higgs particle during this process. You might wonder whether I should worry about the earth pulling on the Higgs particle gravitationally, which would be an external effect that could change its momentum. The answer is that on the short time that it takes for a Higgs to decay, the effect of gravity is so tiny that if I told you how small it is it would make you giggle.  You can forget about it.)  So when the Higgs decays, the energies of the particles that form its debris must add up to 126 GeV, and the momenta of the particles (remembering that momentum is something with size and direction — it is a “vector”, in technical parlance) will add up to zero.

The two massless photons to which the Higgs decays could go off in any direction, but just to keep things simple, let’s imagine they go off vertically, one heading up, the other recoiling from it and heading down. (Why must they go off in opposite directions? Hang on a second…)

How much momentum must these two photons have? Well, that’s easy. First, the total momentum of the system — the sum of the two photons’ momenta — must be equal to zero, since the Higgs before the decay has zero momentum (from Peter’s point of view). Now each photon has a momentum that has a size and a direction. The only way these two momenta could add to zero is if they have equal size and opposite directions. So if one goes up, the other has to go down, and they have to have equal size.

Fig. 8: What Peter sees, more precisely; the Higgs at rest has E = m c-squared, and decays to two photons that each carry off half the Higgs particle’s energy and have momentum p = E/c pointing in opposite directions, so as to perfectly cancel.

Second, the total energy of the system is just the sum of the two photons’ energies. (That’s because there is no interaction-energy between them [except an unbelievably minuscule gravitational energy which you can forget about]. Of course, since they have no masses, all their energy is in motion-energy.) Moreover, for a massless particle like a photon, Einstein’s equation #1 implies that E = p c, where p is the size of the particle’s momentum. Because of this, the two photons, which have momenta of equal size, must also have energies of equal size too. And since the two energies must sum to the energy of the Higgs particle, each photon must have energy equal to one half of the Higgs particle’s energy:

  • E1 = E2 = 1/2 (126 GeV) = 63 GeV.

and since p = E/c for a massless particle,

  • p1 = 63 GeV/c   upward
  • p2 = 63 GeV/c   downward.

This is summarized in Figure 8.

Energy and momentum are conserved, but mass of the objects is not, since the photons are massless and the Higgs was not.  What about the mass of the system?  What is the mass of the system of two photons?  It isn’t zero.  In fact it is obvious what it is. Just as for the Higgs itself (which initially made up the entire system), the system of two photons has the same energy and momentum as the Higgs did to start with,

  • Esystem = E1 + E2 = 63 GeV + 63 GeV = 126 GeV
  • psystem = p1 (up) + p2 (down) = 63 GeV/c up + 63 GeV/c down = 0

And since psystem = 0 for Peter,

  • msystem = Esystem / c2 = 126 GeV/c2

which is the Higgs mass; the system’s mass did not change during the decay, as we expected.

An Observer Who Views the Higgs As Moving Up

Marie is moving downward relative to Peter, so from her point of view, Peter and the Higgs are moving upward relative to her. Let’s say that the Higgs has a speed of v = 0.8 c, or 4/5 the speed of light, relative to her.  Unlike Peter, she views the Higgs as having non-zero momentum, and similarly views the photons as having unequal, though still opposite, momenta, so that the sum of their momenta isn’t zero.

Fig. 9: How Marie views the Higgs decay. The Higgs is initially moving upward, so it has non-zero momentum and larger energy than from Peter’s point of view (Figure 8). The photons to which it decays have unequal momentum from Marie’s point of view.

How are we going to figure out how much momentum and energy the Higgs has, and the two photons to which it decays, from Marie’s perspective? Well, to do this we need one more set of simple equations from Einstein. Suppose from one observer’s perspective an object has momentum p and energy E. Then, from the perspective of a second person who is moving with speed v along (or opposite) the same direction that the object is moving, the object will have momentum p and energy E given by the equations

  • p = γ (p+ v E/c2)      (equation #3)
  • E = γ (E + v p)           (equation #4)

where γ satisfies yet another Pythagorean relationship

  • 1 = v2/c2 + 1/γ2     (equation #5)

according to Einstein. This allows us to convert between what Peter observes and what Marie (or any other observer moving at the speed v) observes.  What we’re about to find is illustrated in Figure 9.

To compare Marie’s views to Peter’s views, we need v and γ.  I claim

  • if v=4/5 c,
  • then γ = 5/3.

[Check:  using equation #5,  1 = (4/5)2 + (3/5)2 = 16/25 + 9/25 = 25/25 .]

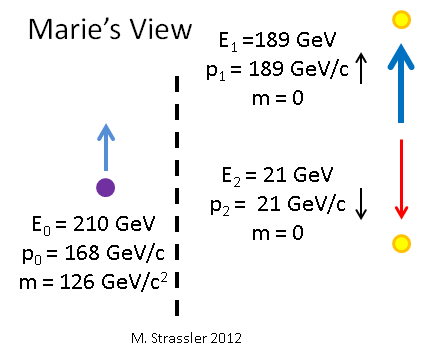
Peter says: the Higgs has p0=0, E0=126 GeV. What about Marie?  She says: the Higgs has

  • p0 = γ v E0 = (5/3) (4/5) E0 = 168 GeV/c upward, and
  • E0 = γ E0 = (5/3) E0 = 210 GeV

Meanwhile Peter says the that two photons have E1 = E2 = 63 GeV and each has E = p c. Then we can figure out using equations #3 and #4 that Marie will observe

  • E1= γ (1+v)E1 = 189 GeV ,   p1 = E1/c (moving upward)
  • E2= γ (1-v) E2= 21 GeV ,      p2 =E2/c (moving downward).

It works! Energy is conserved, according to Marie, because

  • E0 = 210 GeV
  • E1 + E2 = (189 + 21) GeV = 210 GeV

and momentum is also conserved

  • p0 = 168 GeV/c upward
  • p1 + p2 = 189 GeV/c upward + 21 GeV/c downward = (189 – 21) GeV/c upward = 168 GeV/c upward

And the mass of the system is equal to the Higgs mass both before and after the decay, because both before and after the decay,

  • Esystem = 210 GeV
  • psystem = 168 GeV/c upward

which (from equation #1′) makes the mass of the system again 126 GeV/c2, as it was for Peter, since

  • 2102 = 1682 + 1262

An Observer Who Views the Higgs As Moving To The Right

Ok, now what about Chris? Chris is moving to the left relative to Peter, also, to keep things simple, at speed v=4/5 c, so relative to Chris the Higgs (and Peter) are moving to the right at speed v = 4/5 c. Now the same calculation that we did for Marie tells us that the Higgs energy is E0 = 210 GeV and p0= 168 GeV, but unlike for Marie, for whom the Higgs is moving upward, for Chris the Higgs’ momentum is to the right. This is illustrated in Figure 10.

Fig. 10: Chris views the Higgs as moving to the right, so the photons to which it decays have momenta which are partly up and down and partly to the right. The total momentum of each photon consists of 84 GeV/c directed to the right and 63 GeV/c directed up or down; combined via the Pythagorean theorem (see the inset) this gives a momentum of size 105 GeV/c for both photons, and therefore both have energy of 105 GeV.

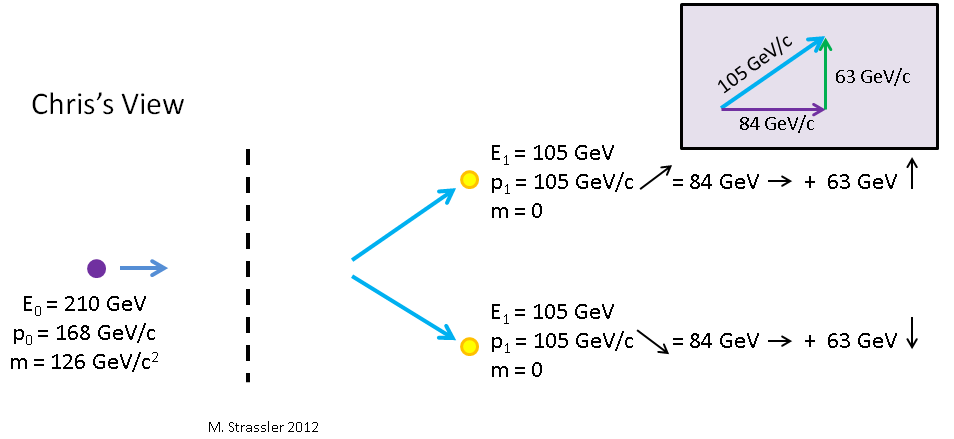
Now the Higgs decays to two photons. If from Peter’s perspective the two photons are moving upward and downward, for Chris, who sees the Higgs and Peter moving to the right, one of the photons will be moving up and to the right, while the other will be moving down and to the right, as shown in Figure 10. What will their momentum and energy be?

Well, we can’t answer this with equations #4 and #5, because those were appropriate for particles and observers moving in the same direction. Now we have an observer moving to the left and photons moving up and down. For this case, the equations are

  • up-down part of p = up-down part of p
  • right-left part of p = γ ([right-left part of p] + v E/c2)
  • E = γ (E + v [right-left part of p])

And these equations are going to be simpler than they look, because from Peter’s point of view, p has no right-left part; all the momentum is either up or down. So Chris sees the Higgs as having

  • up-down part of p0 = up-down part of p0 = 0
  • right-left part of p0 = γ v E0/c2 = (5/3) (4/5)126 GeV/c = 168 GeV/c rightward
  • E = γ E0 = (5/3) 126 GeV = 210 GeV

and sees the upward-going photon has having

  • up-down part of p0 = up-down part of p1 = 63 GeV/c upward
  • right-left part of p0 = γ v E1 = (5/3) (4/5) 63 GeV/c = 84 GeV/c rightward
  • E = γ E0 = (5/3) 63 GeV = 105 GeV

with the formulas for the second photon being the same except that its up-down part points downward. Notice that E = p c for both photons, using the Pythagorean theorem for the size p of each photon’s momentum — see the inset in Figure 10 —

  • p12  =  (upward part of p1)2 + (rightward part of p1)2
  • in other words: (105 GeV/c)2 =  (63 GeV/c)2 + (84 GeV/c)2

which you can check with a calculator is correct (or you can divide by 212 first and verify it by hand.)

So again Chris observes completely different energies and momenta than Peter and Marie. But Chris still sees energy and momentum are conserved, as you can see from the summary of the numbers given in Figure 10.  And Chris also sees that the system of two photons has a mass equal to the mass of the Higgs.  Why?  The total up-down part of the system’s momentum is zero; it cancels between the two photons.  The left-right part of the system’s momentum is 168 GeV/c; the total energy of the system is 210 GeV; and that’s just what Marie saw, with the only difference that she had the system’s momentum going up instead of to the right.  But the direction of the momentum doesn’t affect equation #1′ ; only the size of the momentum appears there.  So, like Marie, Chris also sees that the mass of the system of two photons is 126 GeV/c2, the mass of the initial Higgs particle.

Summing Up

So — we see that the three different observers

  • Disagree about how much energy and momentum the Higgs has
  • Disagree about how much energy and momentum each of the two photons has
  • Agree that energy and momentum are conserved in the decay
  • Agree therefore that the mass of the system is conserved in the decay
  • Agree also that the mass of the system is 126 GeV/c2
  • Agree moreover that the sum of the masses of the objects in the system was not conserved; it has decreased to zero from 126 GeV/c2.

This is no accident.  Einstein knew that energy and momentum were conserved according to previous experiments, so he sought (and found) equations that would preserve this feature of the world.  And he also discovered along the way that the mass of a system would have to satisfy equation #1′.

Bonus: How This is Used to Seek the Higgs Particle

And now, as a bonus, you get to learn how particle physicists try to discovery the Higgs particle. What they do is

  • look at proton-proton collisions that produce two photons
  • compute the mass of the system of two photons (the invariant mass of the pair of photons, in technical jargon)

Whenever a Higgs particle is produced and decays to two photons, no matter how fast and in what direction the Higgs particle is moving relative to the laboratory, the system of two photons to which it decays will always have mass equal to the mass of the Higgs particle that produced the two photons! So unlike random processes that make two photons, which will form a system with a random mass, the Higgs particles will always produce a system of two photons with the same mass. And so if Higgs particles are being produced in the data, and if they are decaying sometimes to two photons, we expect to see a peak from the Higgs decays over a smooth background from other, random processes. This is, in fact, what we see a hint of in current Large Hadron Collider data; and during 2012, if all goes well we will either see the peak in the data firm up and become convincing, or we will see it retreat and disappear.  And if the peak is there, the location of the peak — the mass shared by a surprising number of two-photon events — tells us the mass of the Higgs particle.  And we did!!!

197 Responses

  1. Pingback: Gravitace III - new Age new power

  2. “Mass, however, is completely different from energy and momentum. First, unlike energy and momentum, mass is simply not conserved.”
    ..sometime later
    “the mass of a system of objects is the only thing on our list that is both conserved and agreed by all observers. ”

    I realize you provided “corrections” in later posts but physics aside, statements such as these, are contradictory in logic and hopefully will be sorted out in your book. You mentioned that amateurs produce equations that are not self-consistent, but so also should be the text describing them. I have great admiration for those brave and intelligent to write a book. All of my friends are books, as in general I find humans annoying.

    Reply

    1. Thanks for pointing this out. It’s an old post, and I agree, looking back on this, that this is not nearly as clear as it should be. The point is: for a completely isolated system of objects, (a) the sum of the masses [to be more precise, rest masses] of objects within a system is not conserved, while (b) the mass [that is, rest mass] of the system (which is *not* equal to the sum of the masses of the objects within the system) is conserved. For instance: suppose I put a Higgs boson inside a mirrored box, and then the Higgs boson decays to two photons that will bounce around within the box forever. The rest mass of the Higgs boson is gone, replaced by two photons with no rest mass. The sum of the rest masses of the objects inside the box has changed. Nevertheless the rest mass of the system of objects remains equal to the Higgs boson’s rest mass: the invariant mass of the two photons, which is computed not from their rest masses but from their energy and momentum, is the same as the rest mass of the Higgs boson we started with. That has to be the case, because if the box is stationary, then (a) energy E inside the box is conserved, (b) total momentum of the box is zero, and so (c) the rest mass of the system of objects inside the box is just E/c^2, and this is conserved because E is conserved.

      Reply

  3. Thanks Matt,

    All very easy and straight forward, thanks.

    The first question, and for me (Engineer – maybe the worst kind of hobbies), the physics seems to ignore internal energy (aka heat). For me reading the words, momentum/movement seems to include the notion of vibrational energy, but it isn’t really followed through.

    For example I started my search looking for how to create matter from energy. The answer was adding two photons to make the Higgs particle, which sort of isn’t what I was looking for, because your starting with two particles.

    Anyway this brought me through a link on another one of your pages to here. Previously (probably on your other page), discussed of soft gamma particles and hard gamma particles (or similar). The soft and hard seemed to me to embody higher or lower energy levels?

    Anyway, if we go back to your example, happy to just look at Peters perspective, the Higgs particle at absolute zero (-273^C) or at 10,000^C has different Energy levels. Conservation requires this to be true after conversion to 2 protons.

    I assume this thermal energy changes, (more thermal energy shortens) the wavelength of the emitted protons?

    My mind imagines that splitting anything exactly in half is “impossible” so one proton would/could have more energy than the other. Conservation of momentum requires that of both particles travelled at the same speed =C then both are required to have the same mass. Awesome, but light/photons have a wave nature and energy is stored in the wavelength.

    This however has the same issue, if the speed and mass is the same (discrete package), then the wavelength has to be the same. In an explosion that breaks a particle in to two uneven peace’s the smaller particle simply travels faster to conserve momentum.

    One issues that arises is the vibrational momentum of internal energy. At the atomic level we see particals literally vibrating. At the instant the protons are emitted/created, was the Higgs particle in ossilation and therefore had physical momentum or was it stationary (as periodically required by ossilations)? And if it is in motion is this conveyed to the proton packages? Likely yes, and yes. But is it easy to see which proton attracted the higher wavelength? The proton emitted in the direction of the vibration, conservation of vibrational momentum or the photon emitted in the opposite direction? (Although I concede this vibrational movement is likely to resemble an electron cloud rather than polar (bi-directional) vibration and may indeed never be static. Which also raises issues with the generations of Higgs particles and our ability to know and understand their nature. Are they created and/or do they exist at a discrete internal energy level? Do they, can they vibrate?

    The second question I have (and it is probably covered else on your site), momentum is p = mv

    If mass = 0, P = 0,

    Instead m(proton) = 1.67 x 10^(-27) kg 0

    P = (gama) m v
    It looks like your using (gama) in your maths, but skirt around the issue by rearranging Einstein’s theory.

    Reply

  4. Se puede establecer una relación universal entre Ecinética, Momento y masa sin C.
    Quiero informar que se comete el error de considerar que si una partícula no tiene masa en reposo necesariamente carece de ella.
    Esto aparece cuando dicen que E/p=C es para las partículas sin masa, cuando debía decir que es válido para partículas sin masa en reposo.

    Reply

  5. First of all I want to thank you for this fantastic website, It has been very useful to clarify my ideas About mass and energy. Now here it is my confusion: I can understand that an object in motion acquires kinetic energy, but I cannot understand how an object at rest like an elementary particle can have energy. What is it that makes the object at rest have energy?

    Reply
  6. Pingback: Newtonian Gravity Vs General Relativity – subratachak
  7. Pingback: Trovoadas provocam reacções nucleares!

  8. PROPERTIES OF THE MATTER
    Matter has the following fundamental properties:
    First. It is indestructible, and exists in infinite quantity. For which the nothing has not existed, does not exist, and will never exist, and the laws of conservation are generated. The universal order comes from the immutable character of the properties of the primordial components of matter.
    Second. Matter is impenetrable at very short distances. It is and has its own space. At great distances the spaces of atoms are penetrable, being fields and overlapping, generating ordinary space, which is, as it is said, property of matter, and can not be empty, since it is itself matter.
    Third. Matter is composed of atoms. The atomic components of Matter have energy or inertia, are heterogeneous with each other, and the character of heterogeneity is energetic or inertial, so they generate movement and opposition to it, the tendency to repose, universal, and Universal diversity.
    Fourth. By virtue of their energy or inertia, the atoms of matter with energy and the atoms of matter with inertia are contradictory among them; they apply forces out of themselves and therefore become ponderable. These atoms are components of the so-called chemical elements.
    Fifth. The atoms are associated with each other by their energy. Or by their inertia, that is, they integrate with each other those of the same essence, and by their association, of those who move, those of the dynamic essence, generate universal movement, Life, the universal process of evolutionary integration and universal diversity, and those of the static essence, which oppose life, generate gravity and inertia and try to stop progress by tending to rest, without respite.
    Sixth. The existence and form of being of matter do not depend on whether any Being is observing it, that is, it exists by itself and is, and therefore has an objective character.
    Seventh. It is knowable by itself being an integrated being. And, it reiterates, it generates the knowledge of itself, by itself.
    Eighth. Its properties are immanent to it, that is, they constitute it, and were not created.
    Ninth. Life is the property of dynamic matter. This property manifests as organic life when a dynamic entity reaches a certain level of evolutionary integration, that of algae, for example, in which the phenomenon of individuation appears for the first time in the history of the process of evolutionary integration. And much later, in due time, consciousness appears in the beings who reached the last level of evolutionary integration, achieved to date.
    1/ The definition of atom that is used is: the atom as basic and indivisible block that composes the matter of the universe, that was postulated by the atomistic school in Ancient Greece, Century V A.C., being Democritus one of its exponents.
    Vázquez-Reyna, Mario (2008). Teoría general de la Materia. Borrador. Ciudad de México.

    Reply
  9. Pingback: Ciencias Ocultas. Parte III. ELECTRODINAMICA RELATIVISTA – Ing. Ramiro Galindo

  10. PROPERTIES OF THE MATTER
    Matter has the following fundamental properties:
    First. It is indestructible, and exists in infinite quantity. For which the nothing has not existed, does not exist, and will never exist, and the laws of conservation are generated. The universal order comes from the immutable character of the properties of the primordial components of matter.
    Second. Matter is impenetrable at very short distances. It is and has its own space. At great distances the spaces of atoms are penetrable, being fields and overlapping, generating ordinary space, which is, as it is said, property of matter, and can not be empty, since it is itself matter.
    Third. Matter is composed of atoms1. The atomic components of Matter have energy or inertia, are heterogeneous with each other, and the character of heterogeneity is energetic or inertial, so they generate movement and opposition to it, the tendency to repose, universal, and Universal diversity.
    Fourth. By virtue of their energy or inertia, the atoms of matter with energy and the atoms of matter with inertia are contradictory among them; they apply forces out of themselves and therefore become ponderable. These atoms are components of the so-called chemical elements.
    Fifth. The atoms are associated with each other by their energy, or by their inertia, that is, they integrate with each other those of the same essence, and by their association, of those who move, those of the dynamic essence, generate universal movement, Life, the universal process of evolutionary integration and universal diversity, and those of the static essence, which oppose life, generate gravity and inertia and try to stop progress by tending to rest, without respite.
    Sixth. The existence and form of being of matter do not depend on whether any Being is observing it, that is, it exists by itself and is, and therefore has an objective character.
    Seventh. It is knowable by itself being an integrated being. And, it reiterates, it generates the knowledge of itself, by itself.
    Eighth. Its properties are immanent to it, that is, they constitute it, and were not created.
    Ninth. Life is the property of dynamic matter. This property manifests as organic life when a dynamic entity reaches a certain level of evolutionary integration, that of algae, for example, in which the phenomenon of individuation appears for the first time in the history of the process of evolutionary integration. And much later, in due time, consciousness appears in the beings who reached the last level of evolutionary integration, achieved to date.

    1/ The definition of atom that is used is: the atom as basic and indivisible block that composes the matter of the universe, that was postulated by the atomistic school in Ancient Greece, Century V A.C., being Democritus one of its exponents.

    Vázquez-Reyna, Mario (2008). Teoría general de la Materia. Borrador. Ciudad de México.

    Reply

  11. Is it right to say that matter is energy? I mean is like the elementary particles are highly concentrated form of energy?

    Reply
  13. Pingback: Significance Of Gibbs Free Energy | Life Free Energy

  14. Matt –
    Great article, the best and most enlightening one I’ve found. One small thing still bugs me though (apologies if it has been covered and I missed it). Where does INERTIA come in all this? As an object moves faster, its (rest) mass stays the same, so does its inertia stay constant while its total energy increases?
    Many thanks,
    Doug.

    Reply

    1. Mass is usually, as I know, defined circular as that which has inertia. So if something has inertia then it has mass and if something has mass then it has inertia. So where ever mass comes from, inertia probably follows suit.

      Reply

  15. ## IMPORTANTT ##
    i think less mass contains more energy…..no not an cotton and iron contains same amount of enrgy. What about e=mc2 that is c2=e/m and i think energy and mass is directly opposite in maths…..thats why speed of light is contant because photons is the smallest particle ever discoverd and have very less mass…..i know theory says light have no mass but it have…no mass=not present….yeh i know light is a wave but in other form…..think you running in a ground with your child and you both have equal energy who runs fast surely your child because you have more mass then him!….. and by my theory if we use some energy like Newton’s law(object in motion will stay…..) in some direction we keep moving because the energy releases in higgsfield and it keep you moving because of rapid bouncig but more in one direction…. pleasee dont think that it is fake please read it again think about it and try to understand…. i’m just 14 years old child wants to be astrophysicit and i already makes some more theaories on time travel….box theory (dimensional)…and others please call me on 9454306419 (talk in hindi) if you like this comment and want to keep this theory upgrade…thanxx 😊

    Reply

  16. i think less mass contains more energy…..no not an cotton and iron contains same amount of enrgy. What about e=mc2 that is c2=e/m and i think energy and mass is directly opposite in maths…..thats why speed of light is contant because photons is the smallest particle ever discoverd and have very less mass…..i know theory says light have no mass but it have…no mass=not present….yeh i know light is a wave but in other form…..think you running in a ground with your child and you both have equal energy who runs fast surely your child because you have more mass then him!….. and by my theory if we use some energy like Newton’s law(object in motion will stay…..) in some direction we keep moving because the energy releases in higgsfield and it keep you moving because of rapid bouncig but more in one direction…. pleasee dont think that it is fake please read it again think about it and try to understand…. i’m just 14 years old child wants to be astrophysicit and i already makes some more theaories on time travel….box theory (dimensional)…and others

    Reply
  17. Pingback: Is it possible for pure energy to have mass? | Physics Forums - The Fusion of Science and Community

  18. P.S. to my comment just above:

    I found a 2011 paper that adopts a similar viewpoint: http://arxiv.org/pdf/1102.1170

    The author—an Italian engineer at Fiat, apparently—starts with Minkowski spacetime and Noether’s theorem to derive the conservation of energy and momentum. From there, and without reference to anything called “mass,” he defines rest energy, kinetic energy, force, and acceleration.

    Finally, he points out that the emergent E_0/c^2 term corresponds to what was called inertial mass in classical physics. He then DEFINES inertial mass as E_0/c^2.

    He concludes that inertial mass is worth retaining in relativity, but only for practical reasons (not conceptual ones). He reckons that the c^2 conversion factor, which is only there because we measure time and space in different units, usefully emphasizes the surprising bigness of E_0, and also that mass is easier to measure than E_0. I’m not entirely persuaded.

    Reply

  19. I know this is a triviality but I prefer to define the speed of light as 1 (just alter the units of definition).

    And, although it leaves the unit conversion factors unstated, the simple form E=M simpler to write and
    yields, in my opinion, a better intuition

    It also rids us of the very misleading yet oft repeated statement that “the reason E=MC^2 yields such
    HUGE amounts of energy is because C is so LARGE”. Huge and large are not valid terms of physics.

    – greg.

    Reply

  20. Hi Matt,

    I’ve been thinking about Frank Wilczek’s idea of “mass without mass”—i.e., that the vast majority of a system’s mass (E_0/c^2) arises not from the mass-energies of its constituent fundamental particles, but rather from motion-energy and interaction energy and other field energy (to use this site’s lingo). To drive the point home, he explains that modeling quarks as massless gives nearly correct results for the masses of protons and neutrons. “QCD Lite,” he calls this.

    With the recent detection of the Higgs, it seems to me that we now have experimental justification to take this one step further: even the mass-energy of fundamental particles can be thought of as “mass without mass,” arising as it does from “the energy [a particle] picks up when sitting in a non-zero Higgs field” (your words: http://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-known-apparently-elementary-particles/the-known-particles-if-the-higgs-field-were-zero).

    It’s as if mass isn’t truly fundamental at all. Energy is and momentum is (thanks, Noether!), but mass? At every level, from macroscopic systems down to the “system” of a single electron, it’s just rest energy (divided by c^2), isn’t it?

    Hell, when Einstein gave us m=E_0/c^2 (not E_0=mc^2, mind), he could have added a third line to that equals sign: m≡E_0/c^2.

    I’m starting to view mass as nothing more than a mathematical shorthand, on a par with β≡v/c, or γ≡1/(1-β^2)^-1/2.

    Which brings me to my real point: why not do away with the concept of mass altogether? Why not just write E_0/c^2 instead of m? Sure, some equations would become a tad more cumbersome, but not all of them:

    E^2 = (mc^2)^2 + (pc)^2

    vs.

    E^2 = E_0^2 + (pc)^2

    But even if m is on balance a useful mathematical shorthand, I’m wondering if mass adds anything useful CONCEPTUALLY. Could it actually be a hindrance to understanding?

    We all have prior associations with m before we start to learn relativity. We think of it as the “gravitational charge” and as the fixed ratio of a closed system’s momentum to its velocity. Then we get to Einstein and discover that neither of these prior associations is true beyond the classical limit. In fact, it is energy and momentum that can be thought of as “gravitational charge,” and the ratio of a system’s momentum to its velocity isn’t fixed but is rather a function of the system’s velocity and rest energy (AKA “relativistic mass,” which has already been mostly done away with because of the confusion it causes).

    So once we get to relativity, why do we cling to a concept of “mass” at all? We’re not preserving anything old, other than the word itself. That seems like a recipe for confusion. We can even avoid m when we derive the classical limit, yielding:

    a_g = GE_0/((c^2)(r^2))

    and

    p/v = E_0/c^2

    If we introduce m in relativity at all, why not emphasize that it’s merely a mathematical shorthand for E_0/c^2, similar to β and γ? Are there compelling reasons to maintain mass as a key physical concept?

    I get that m is the frame-independent magnitude of the four-momentum, and that’s important, but again, we can simply replace it with E_0/c^2 (or, in units where c=1, just E_0). So when you say that the mass of a closed system is special because it is “the only thing on our list that is both conserved and agreed by all observers,” couldn’t you equivalently say that everybody agrees on how much energy the system has at rest?

    By treating mass as its own concept rather than as a mere mathematical shorthand, don’t we risk distracting ourselves from the fundamental energy-conservation principle? Even physicists often talk loosely of “converting” mass to energy, but if we drop the very idea of mass, it becomes crystal clear that the phenomenon of interest is the conversion of rest energy to other forms of energy.

    It’s like “mass” is just there to impress upon us how very much rest energy things have. Gets the c^2 in there. But it’s a circular concept, isn’t it? I mean, multiplying mass by c^2 to get E_0 is equivalent to un-dividing E_0 by c^2, which is what we did to define the mass in the first place. It’s almost an accounting trick. But forget about mass entirely, and the situation is pretty straightforward: a system’s rest energy is calculated through simple addition of its constituent energy contributions; and if some of that energy escapes (say, through radiation), calculating the system’s remaining rest energy is simple subtraction.

    So in summary, it seems to me that energy and momentum are rightly regarded as fundamental, whereas mass is a concept defined in terms of (rest) energy that can be profitably discarded. Of course, there are plenty of useful concepts that are defined in terms of more fundamental ones, and I’m certainly not saying that we should bin them all. But mass in relativity isn’t just reducible to something more fundamental; it is, for me, confusing and distracting.

    But maybe it’s conceptually useful in ways I’m unaware of.

    Reply

  21. Woah! I’m really enjoying the template/theme of this blog.
    It’s simple, yet effective. A lot of times it’s
    very difficult to get that “perfect balance” between user friendliness and visual appearance.

    I must say that you’ve done a superb job with this.
    Also, the blog loads very fast for me on Opera. Outstanding Blog!

    Reply

  22. Hi Matt,
    I’ve been searching out an adequate response to a problem I’ve been having, and have found your article as the most well articulated on the subject (especially to a non-physicist), and was wondering if I might bother you with my query.

    Whilst we will find a vastly different stance on the relevance of this question, dependent on whether we speak from a position of physics on one hand, or philosophy on the other, I think regardless that is has some importance.

    The subject is on tautology, and regards the nature of equivalence between E on the one side, with MC2 on the other.

    The problem is as to whether the equivalence stands in such a nature as to validate the proposition that with what we know, we might not include either within the definition of E (or MC2) the definition of the other as a constituent part?

    That is to say: given what we know, can the one be inferred given the other?

    I’m sure you’ll be more than familiar with what I’m going for, but regardless I cannot find sense of it anywhere! I’ll even be very satisfied with being told how fallacious my thinking is, so long as I can understand! So please if you could respond with as little technicality as you can.

    Thanks for your time in advance!

    Reply

  23. Isn’t there a disconnect between equations 1 and 2? If I use p = m*v for momentum, then equation 1 can be rewritten E = m*c*SQRT(v^2 + c^2) and equation 2 can be rewritten as E = m*c^2. Where’s my error?

    Reply

      1. In his next example, however, where mass is considered 0, shouldn’t the value of p also equal to 0? I understand that p is small when v is very small with respect to c, so the p*c side becomes smaller, but when mass approaches 0, shouldn’t the momentum, by definition, approach 0 too? In which case the p*c side would also become smaller.

        What I believe is wrong is the fact that, like stated in the article, we are using simple trigonometric ratios to deal with these equations. I suppose this problem can be solved if using hyperbolic functions. Or am I wrong somewhere? Please enlighten me.

        Reply

        1. “…it is the conserved quantity that, in any physical system with time-independent equations, can be written down using Noether’s theorem. Give me a physical system with equations that describe it; I will write down for you what E is. ” … Prof. Strassler

          Al for particles with no mass (zero rest mass) the energy (Prof. Strassler calls it “the conserve quantity”), like photons, bosons, the energy can be formulated as E=hv. The energy is still there we just use different equations to describe it w.r.t. the parameters available in that particular state, (m & c) or (h & v). The “conserved quantity” is still there “conserved”, :-).

          PS; Prof. Strassler, if I can jump to another topic, as usual, sorry, :-). I count three (3) rotations that make up the electron, two (2) “trapped gamma photons” and their resultant, the wobble created by that fact that the symmetry is broken. My interpretation of the electron is two gamma photons locked in this little space with their momentum vectors balancing on a “point” trapped”, held together by an external field (maybe even dark energy) that will maintain this balance on this “point” in space. If all this hypothesis is anywhere close, is this “point” really a point or can it be an empty spherical space (pure vacuum, not even a single field in it or through it, empty)?

          My point being, if it is an empty spherical space in the centre of an electron then it could shed light into Einstein’s curved space concept of gravity and quantum gravity, i.e. the circumference of the empty spherical space in the heart of an electron is the smallest radius space can have and as you go radially outwards the radii, of course get larger and it is this difference is space topology that creates the various fields, including gravity, that we “see”.

          Hope you are having fun with the emulated software, :-).

          Reply

  25. First, great website and articles.

    Second, I’m confused by your use of “mass-energy”.
    As established by mass-energy equivalence and Einstein’s equation, the addition of ANY form of energy to an object increases their mass. Any kind of energy there is also comes with an increase of mass. Why make a new category that is “more mass” than the others?
    It almost feels like an admission of the point you debated in “Matter and Energy: A False Dichotomy” because it seems to imply that this energy arises directly from matter, therefore energy=matter…
    Since the other forms of energy on your list clearly add mass (kinetic or “movement” energy’s for example is famously illustrated by the ‘impassable speed of light’ limit), shouldn’t this category perhaps have some other, better name?

    Reply

  27. Forgive me if this as a duplicate comment or already answered by the article but over the decades I have become increasingly upset by what I view as an abandonment of the spirit of relativity by popular science and scientists.

    There are no properties called “speed” or “velocity” or “momentum” that belong to a particle nor “wavelength”, “frequency”, or “energy” that can be assigned to a photon.

    All of these properties can ONLY be assigned to particles/waves taken two at a time. Two particles in a pair cannot be assigned particle specific velocity: only the pair of particles which can be as assigned a speed of approach or retreat.

    Is this not true? I’m not sure but I don’t think you can assign direction (vector) values to them either as I think that would require a third particle. I know this view would probably be characterized as Machian, but I really still like him even though Eistein withdrew from him.

    If I’m right then I maintain we do our future scientists a great misduty by not teaching them “right speak” (how Orwellian) from the outset. Wrong use of words impairs imagination, just as Einstein did when he insisted that all proposed properties (at the minimum) must be defined in the terms of the experimental setup used to measure them.

    That is, “properties” have no meaning only results do.

    Reply
  28. Pingback: Quora

    1. There is no way to infer the total mass-energy of the universe is constant because it can’t even be defined without knowing the large scale structure of the universe, which is unknown. Things get very tricky when you’re trying to look at the universe as a whole…

      Reply

  30. Proffessor Strassler,
    Thank you for this clear insight in the relation between energy, mass and momentum. Especially the example with the Higgs particle explains how it works. Still, it appears as if the term ‘mass’ is used in an inconsistent way. When explaining Peter’s view, you say ‘the Higgs with its mass of m=126 Gev/c2, has energy E0 = mc2 = 126 Gev”. Later, when explaining Chris’ view, you say: “So, like Marie, Chris oalso sees that the mass of the system of two photons is 126 Gev/c2.’ . This follows from the ‘definition’ of the system mass by dividing the Energy by c2.
    In Figure 10 on the side after the breakdown of the Higgs particle in Photons, you write for both photoms ‘m=0’. While the mass of the combined photons is 126 GeV. So clearly, the term ‘mass’ can only be used for the complete system. Before the Higgs particle breaks down, the system consists of a single particle, and the mass can be derived from the energy and momentum. Since V=0, we should find ‘the mass of the Higgs particle can be derived from its energy of 126 Gev’. The other way round is confusing. (By the way, in the right part of fig. 10 the 84 GeV should be divided by c).
    From your article I finally got to understand that mass is in fact a way to balance the energy/momentum budget. Your article also shows that there are two distinct aspects that should be distinguished. On the one hand, there are ‘events’ in which a number of properties of (a set of) particles can change instantly while other properties do not change, at a certain location in spacetime (like the transformation from Higgs particle into two photons). On the other hand, it is possible to consider such an event from different reference frames, like Peter, Marie’s and Chris’ view.
    This can be described in a more general way: consider some event in spacetime, like this transformation of the Higgs particle. This takes place in reference frame S. We can define an infinite set of moving reference frames each with a velocity component in x, y and z direction with a value between –c and + c. For each frame, the value of E and p can be different. The Lorenz transformations take us from one frame to another one. In the spacetime four-vector, we can describe this as hyperboloid surfaces in an x,y, ct space, which I can mentally picture. In the x,y,z, ct frame it will be some sort of hyperboloid volume (?) Well, when going from one frame to another one (only v differs), we will stay on the same hyperboloid surface. I do not know how this spacetime vector is shown in the energy-momentum space, but is it a time derivate multiplied by the restmass, the E, p fourvector. If we consider the x,y, ct space only, this is likely to be also some hyperboloid surface. Going from one frame to another one means of the Lorenz transformations, some parameter remains constant, and that must be the ‘total system mass’. That is why E and p differ for Peter, Chris and Marie but the ‘total system mass’ is the same. So, there seem to be a set of parallel hyperboloid surfaces that distinguish themselves from each other by different values of the ‘total system mass. Is this correct?
    When you move on such a surface, E and p do not remain constant, of course not, v is different. If you consider a certain point in spacetime, which is called ‘an event’, something happens there, for instance a Higgs particle changes into two photons. The Higgs particle coincides with the two photons in the same event. Of course, we do not move on the hyperboloid surface, and both E and p are conserved. We are still in the same spcepoint, on the same surface, so also the ‘total system mass’ also remains unchanges. This is clear.
    What has changed is the mass of the particle. When a Higgs particle is changed into photons, itsl mass disappears. Are there other rules that dictate what happens with the particular masses of the particles?

    Reply

  31. Hello Dr. Strassler,
    I was wondering how mass is different than energy; specifically, what properties does mass have that energy does not?

    You do mention “unlike energy and momentum, mass is simply not conserved” but it is not clear to me that your comparison is a fair one, i.e., mass is more akin to kinetic or potential energy (not individually conserved), and as such simply a part of the total energy of a system, which is unambiguously conserved.

    I have always taken mass to be “all those internal energies who’s details we need not calculate for the situation under consideration.” If we were to analyze the energy transfers in an automobile collision it would not be necessary to know how all the nuclei acquire some of their energy (mass) through asymptotic freedom as this energy isn’t transferred in the collision and including the cars’ rest energies would be as cumbersome as it is unnecessary. It all gets lumped together and packaged in another term for energy called “mass;” a metaphorical junk drawer for energy terms. At least it has always seemed so to me, but you would know much better than I, so… am I missing something?

    Reply

  32. I’m re-asking an unanswered question that I posted months ago in a more specific area of this fine blog. The question is, imho, an overarching question about the fundamental nature of our Universe.

    Q: In today’s Physics, is the fundamental essence of the Universe still considered to be Space, Time, and Matter — or something more akin to one of the below?

    A. Space, Time, Energy
    B. Space-Time, Matter-Energy
    C. Energy Fields (un-rippled=Space, rippled=Matter, ripple frequency=Time)
    D. Sump’n else

    Reply
  33. Pingback: Are atoms made of matter? - Page 2 - Historum - History Forums

  35. I want to add that in addition to the link Dr. Strassler has provided above (Einstein’s appreciation of Emmy Noether), there is also this link to a New York Times article: http://www.nytimes.com/2012/03/27/science/emmy-noether-the-most-significant-mathematician-youve-never-heard-of.html?_r=0
    Even if Professor Noether had never done a stitch of work in mathematical physics — much less, having established herself as a giant in that field — her work in algebra alone would have qualified her as one of the most influential mathematicians of the 20th Century.

    Reply
  36. Pingback: A Short Break | Of Particular Significance
  37. Pingback: Page not found | Of Particular Significance
  38. Pingback: Mass-ive Source of Confusion | Of Particular Significance

  39. Have you ever considered about adding a little bit more than just your articles?

    I mean, what you say is fundamental and everything. Nevertheless just imagine if you added some great pictures or videos to give your
    posts more, “pop”! Your content is excellent but with images
    and videos, this site could definitely be one of the best in its niche.
    Wonderful blog!

    Reply

  40. Mr Strassler, thank you for taking the time and energy to put up these articles; as a first-year physics undergraduate reading this particular one helped me undertstand the mechanics behind special relativity. I have a question regarding the mathematics involved in your example of “An Observer Who Views the Higgs as Moving Up”. After some working I was still unable to derive the equation you used to find the energy of the two photons as viewed from Marie’s perspective, namely E1= γ (1+v)E’1 and E2 = γ (1-v)E’2, where E’1 and E’2 are the energies of the photons viewed from a stationary observer’s (Peter’s) perspective. Solving equations #3 and #4 only yielded a jumbled, messy expression for p’ and/or E’. How did you do it?

    Reply
  41. Pingback: E es igual a m por c al cuadrado | La Ciencia y sus Demonios
  42. Pingback: TIME for a Little Soul-Searching | Of Particular Significance

  43. Hi Matt
    Thanks for this post, I think it’s very important in order interested people may clearly understand the relatisvistic relationship between energy and mass, usually a complicated one for newcommers.
    I would like to stress two important topics of your explanation:
    (1) No relativistic mass is included (I mean mass depending on the observer); this is the right way to explain relativistic dynamics!
    (2) You stress very carefully the difference between “invariant” (=the same for all observers) and “conserved” (= a physical magnitud whose value remains the same “before” and “after”, but be aware, for the same observer). To talk abount invariance several observers must be involved, to talk about conservation only one observer must be involved, but the same before and after.
    Also I would like to ask you about a topic of your post which is misleading from my point of view.
    When you talk about rest energy, you write E = m c2, and afterwards you say that “this relation does not mean that energy is always equal to mass times c2; only for an object that is not moving (and therefore has zero momentum) is this true”. So that, as I understand the issue, you are using the same symbol, E, both for total energy and rest energy, and you need to clarify with words that when the object is at rest E = m c2 (because when in motion energy is E = m gamma c2).
    I think this way is misleading. Why not to use two symbols for each concept? E for total energy and E0 (sub) for rest energy: E = m gamma c2 and E0 = m c2. This is standard notation in Physics, it’s a lot clearer than using the same symbol for both magnitudes plus adding words explanations, and last but not least, it reinforces one of the greatest physical ideas of relativity: that mass is another form of energy.
    Regards from Spain, Jesús.

    Reply

  44. In your splitting up of energy into three different types, isnt the “mass energy” of a system, just the mass energy of its constituents + the kinetic and +/- the potential energy of them in the rest frame of the system.

    And the mass energy of the constituents is similarly defined all the way down to fundamental particles. Now fundamental particles arnt all maseless, so where does this mass energy come since they have no kinetic energy in their rest frame. Is it potential?

    Also does a systems potential energy due to electro/gravitational fields contribute to its mass, since it still exists in the rest frame, Im talking about the potential of the system as a whole, not the potential interactions of its constituents with each other.

    Reply

    1. 1) in quantum field theory, mass (which is the fundamental frequency of a ripple in a quantum field, i.e. of a quantum, or “particle”) is an effect that you would ascribe to potential energy. All energy in quantum field theory is either kinetic or potential, and mass certainly isn’t in the kinetic energy parts of the equations, so that leaves potential. But it’s sufficiently different from the types of potential energy that we encounter in undergraduate school that I haven’t wanted to emphasize this much; it doesn’t add a lot to your intuition to know this fact.

      2) Your question isn’t well defined. What do you mean by “potential of the system as a whole”? I can see a couple of things you might be trying to say. Give an example, maybe I can figure out what you’re confused about.

      Reply

      1. Thanks for the reply

        For the second part, Im asking would a particle or a system of particles in an electromagnetic field have more rest/invariant mass, than one not in the field due to the potential it has as this energy still exists in the rest frame of the particle/system?

        And for the first part where does the higgs field come into play?

        Reply

  45. Professor, can one say that “the great red spot” of Jupiter, the large storm trapped in Jupiter’s jet streams, is a good analogy of how the universe is constructed? The mass particles are trapped waves in voids of fields permeating across the entire universe. So one would say galaxies are large energy disturbances (storms) trapped in the gravity field that permeates the universe.

    Reply

    1. Hmm — not really. The great red spot, and all of its disturbances, are the result of complex and often turbulent dynamics of the gasses that make up Jupiter’s atmosphere. Collisions among the gas molecules are crucial. The formation of galaxies within the universe is a completely different process, the result in part of dark matter collecting in regions that have slightly higher density after the early Big Bang. Collisions among dark matter particles (or whatever makes up the dark matter, if it turns out not to be particles) are believed to be irrelevant to this process.

      Reply

      1. Sorry for my vague question, again. 🙂 … That was not what I was after. I was using the “trapped” storm, circulation, as a possible analogy as to how standing (trapped, matter) waves could possibly be created. I am not sure whether I am asking for an explanation of the scattering process or more fundamentally the mechanism that turns open waves, photons, into closed (or standing) waves, fermions.

        The great red spot seems to have been generated by vortices created by friction between the layers of gas. In a quantum event when the light radiates out in a spherical wave front could it be that the wave front itself has a sinusoidal profile, (the radiance varies across the surface of the wave front) and hence creates a variable density wave front. Hence, due to the variable density refraction between the adjacent peak or the radiating wave create vortices of photons until the become closed and create a massive standing waves?

        Simple geometry shows that two vortices will be created in each “valley” of the wave front with identical and opposite “symmetrical” rotations. Is it this symmetry the same as that discussed in SUSY? If so, when talking about breaking the symmetry does it mean that on of these closed loops becomes so stable that it is released from it’s opposite (antiparticle) and “pops out” of the vacuum (non zero VEV)?

        So was Dirac correct in his description of antiparticles? Could you please explain where the derivation standing w.r.t. standing wave generation and/or give me some references where I can find it?

        Reply

  46. An excellent article that answered questions I didn’t know I had. (Such as why one RF didn’t see a particle decaying into different particles than another RF.) I have however some lingering questions.

    Firstly, though this doesn’t relate much to mass here, is there a minimum energy a massless particle can have? I know QM has put some rather interesting limits on things such as certainty, motion at absolute zero, length and time, so is there a minimum (Or maximum?) frequency\energy or are there good QM reasons for there being no such limit?

    Alternatively, is there a point where it becomes meaningless to talk of the differences between to energy levels? When the difference becomes small enough do we become unable to meaningfully differentiate two particles with slightly different energies?

    My second question relates to mass but may fit better on an article I haven’t read yet, so forgive if it doesn’t quite fit here. Do we know how much of the mass of a system is due to gravitational potential energy? Obviously moving objects apart stores potential energy in them and since the birth of our universe all the mass in it has been moved away from nearly all the other mass and when I do some back of the envelope calculations I get… nonsense. (I’m neglecting the Higgs field ‘switching on’ and giving particles mass some time after the big bang, as well as inflation moving objects past each others’ event horizons, which I believe means they no longer interact gravitationally or indeed in any manner.)

    Do we have an answer? How would I go about working it out for myself?

    Reply

    1. “is there a minimum energy a massless particle can have?” The smallest energy a massless particle could have would be obtained by giving it a wavelength that stretches across the entire universe, and that would give it a frequency comparable to the age of the universe. Multiply by Planck’s constant and that gives you the minimum energy. That minimum will keep decreasing. You also can’t talk about energy levels closer than this.

      Gravitational potential energy: if you try to look at this from the point of view of the whole universe, you will at some point have to deal with the fact that the universe as a whole is described by Einstein’s equations and concepts, and not Newton’s. For instance, you’d better account for the speed of light and that there’s a limitation of how far away matter can affect us, given the universe’s age appears to be finite.

      But I don’t feel I’m sure what you’re trying to calculate.

      Reply

      1. I possibly should have been more precise. You say we always agree on the mass of a system, if not the momentum and speeds. Does this work with potential energy? Can I (In theory, if not in practice.) calculate the potential energy in a system by comparing the mass of its constituents with the mass of the system as a whole? (This would be easiest given atomic nuclei I guess.)

        On the gravity front, I assumed matter started out as dense as a neutron star then tried to calculate how much energy was required to reduce the density of the universe from that to something similar to molecular gas clouds. (Which I’m taking as an arbitrary estimate of the universe’s current density.) It came out as being more energy than the mass itself would contain, possibly this is due to my calculus being on the brown dwarf side of dismal. Of course if the expansion of space moving things apart doesn’t add potential energy to matter then that confuses things more.

        Basically, if we took all the mass in the universe and let it all fly together, how much gravitational potential energy would be released relative to the amount of mass there is? Would it be an insignificant amount, or does gravitational potential energy account for a large part of what we call ignorantly oft call mass?

        Reply

        1. “Can I (In theory, if not in practice.) calculate the potential energy in a system by comparing the mass of its constituents with the mass of the system as a whole?”

          No — you are forgetting the kinetic energy of the constituents. The only thing you can calculate is the kinetic energy plus the potential energy; to separate the two you need to know about the internal dynamical behavior of the system, which you can’t just get from the mass information.

          Gravity: you’ve made a mistake somewhere. The potential energy of a certain amount of matter distributed with arbitrarily low density is zero; the potential energy of the same matter, in a neutron star, should be comparable to the mass-energy of the matter, not greater. To really do the calculation right you have to account for corrections to Newton’s gravity due to Einstein’s equations… but you should not have gotten something wildly greater.

          Your final question isn’t well posed. What does it mean to let it “all fly together”? Make a black hole out of it? If so, then the gravitational potential energy released is comparable to the mass of the matter. But this does not imply that “gravitational potential energy accounts for a large part of what we call mass”. It’s irrelevant to that point. We can study the mass of an object by pushing on it and seeing how fast it accelerates, knowing nothing about either gravity or the context of the universe.

          A bigger problem with your question is that you’re trying to look at the universe as a whole but are doing so inconsistently. Back when the universe was very dense, it was also extremely hot; it wasn’t like a neutron star at all, which is (relatively speaking) cold, but more like a dense fireball. This tremendous heat affects the behavior of space and time, because gravity reacts not to mass (in Einstein’s theory) but to energy and momentum. It only reacts to mass in the non-relativistic, Newtonian limit, where velocities of particles are rather slow and energy and mass are basically proportional to each other (i.e. E = m c^2 to a good approximation).

          Reply

  47. Excellent and very insightful
    article!
    Just a quick question – is Heisenberg’s uncertainity principle tied to special relativity in any way?

    Reply

    1. Quite the contrary; they are completely independent. Uncertainty comes from quantum mechanics. You can make theories that have Einstein’s relativity and no quantum mechanics, and you can make theories that have quantum mechanics and no Einsteinian relativity; in fact these are the ones we learn first in school. The world has both of them, but didn’t have to, as far as can tell.

      Reply

  48. Matt – very helpful. Could you explain a little how the energy of a photon is related to its frequency/wavelength? Is there a theoretical (or observed) maximum or minimum energy of a photon? Does that depend on the frame of reference of the observer? Thanks,

    Reply

    1. Einstein/Planck/De Broglie: The energy of ANY particle is Planck’s constant times its frequency of oscillation.

      Einstein/De Broglie: The momentum of ANY particle is Planck’s constant divided by its wavelength

      [There are some factors of 2 pi floating around here; be careful depending on which convention you use for Planck’s constant — is it h or h-bar? But this is a detail; I can fix it if you like, and so can you by looking up De Broglie.]

      There is no theoretical maximum or minimum to the frequency or energy of a massless particle. A particle with a mass m cannot have E < m c^2, but again there is no maximum.

      The energy and momentum of a particle do depend on the frame of reference of the observer.

      Reply

  49. the simplest way to put it is ‘for every action is an equal and opposite reaction’…sir issac newton’s theory of pure simplicity standing the test of time,,,governing totality,and every singularity…eternity is a very long time in space,any inbalance beteween space time no matter how insignificantly minute has catastrophic cosequences…if for example; the mass value of the universe increased by as little as one quark for every googlemilllion lightyears,eventually the entire universe would become one block of mass…(please note) if you think im being a little flippant to exagerate,im absolutely not!!mass has an eternity to do it in…as does energy.the first most fundamental law governs from totality to infinite singularity…the higgs bozon,and the higgs field,interact with mass in the same manner as time in space,…
    Time is the equal and opposite reaction,preceeding the action of forming mass,,,just as all mass is basically congealed energy,all of space,is congealed time,both the positive,and negative…quantum at the particular level,yet in general its relative…
    “””space in time,and time in space…the singularity of every totality,in the totality of every singularity..””’

    Reply

  50. One more Q; c is the speed of the EMF ripple /photon , i wonder what is the mechanism that implemented this particular speed over ALL kinds of fields ? why c which is related to EMF forced itself on all other fields?

    Reply

    1. The quantity “c”, though often called “the speed of light”, is actually better described as the “universal speed limit” at which ALL massless particles must travel. This comes from the geometry of space and time, and has nothing to do with light at all. The only reason light travels at the speed limit is that light happens to be made from massless particles. The same is true for gravitational waves.

      Reply

  51. In my question about inertia above, I meant to say “proton” instead of “photon” in the last line.

    Reply

  52. According to Matt. ; mass is the size/ amount / quantity / volume / value of resistance by which it resists being accelerated , o.k. , if gravity goes zero , does same mass will exert same /more/less resistance ? but in space we do not see any resistance so again mass is somehow related to gravity………??? i am asking not stating.
    Sorry for all these questions but your website is really creating a sense of awe in the mind.

    Reply

  53. P.S. ;
    But same cube exerts 100 kilograms per cm^2 in another planet then its mass is 10000 kilograms with same protonic constitution , are all concepts of kilograms a huge mistake ? in wikipedia electron mass is 9.11 * 10^-31 KILOGRAMS , on that other planet would it be 9.11*10^29!!??
    sleep is lost………

    Reply

    1. Mass and weight are very different things.

      Mass measures how much stuff an object contains. It is independent of gravity.

      Weight measures how hard gravity pulls on an object. It is proportional (in the Newtonian limit) to both the mass of the object that is being pulled and the mass of the object that is pulling.

      The weight of an object (in Newtons) changes when you move it from the earth to the moon or another planet. However, the object’s mass (in kilograms) remains the same.

      Reply

  54. Matt. said that if gravity = zero then a cube 10 cm side would have its mass = E of all protons / c^2 (deduction ) , my point is ; suppose that cube is 100 kilograms , here on earth it exerts a pressure of 1 kilogram /cm^2 on 100 cm^ area in vertical direction ( towards center of earth ) , now if gravity goes zero are we going to have pressure in all directions ? then we ask how many kilograms per cm^2 is this pressure ? how much is the mass ? does it remain 100 kilograms ? if not then mass is related to gravity not E …………HERE I AM TOTALLY LOST…HELP NEEDED.

    Reply

  55. I am still in need of matt. to tell what is the physical meaning of m and E ? suppose some ” stuff ” is at relative rest , what is the meaning of its E ? mere m.c^2 ? is it a kind of potentiality , i mean if we manipulated its atoms it will ” explode” ?
    what is the physical meaning of m ? you said m= all energies / c^2 , but what is the mass not in equations but in reality , in the world ? or it is like all sub-particles realm where in principle we know ONLY the mathematical knowledge , never the reality knowledge………..i am following this site posts , till now i found no answer to my grand Q …( grand relative to me ).
    thanks

    Reply

  56. Thanks again for your excellent articles. I have a simple question about the relation of mass and E/c^2. I seem to remember that the characteristic of mass is its inertia. When you apply a force to a massive object, you feel an opposing force, work may be done, and the object may be accelerated. In your example using a Higgs boson, one may certainly (if you are fast enough) push on it and even measure its mass by measuring the resultant acceleration. However, in the next instant, it is replaced by 2 photons. They have an equivalent mass, E/c^2, to the Higgs boson, yet you can’t push on them. Thus it seems that there is a tangible difference between the two systems, even though they have the same E/c^2.
    I guess, from what I remember of your discussion of the interior of the photon, that somehow you will say that the equivalent mass will somehow have an equivalent inertia.

    Reply

    1. That is correct. If you could practically push on the two photons as a collective system, they would behave as though they had an equivalent inertia, according to special relativity. The technical difficulty of doing so does not make the in-principle experiment impossible… and any in-principle experiment should have a sensible answer consistent with all other in-principle experiments, including those that are practical to carry out and those that aren’t. (This is not a new way of thinking. To my limited knowledge, hopefully correct, even Newton considered what would happen if a ball were thrown with greater and greater velocity [ignoring air resistance, mountains, and other practicalities] — realizing that with sufficient velocity it would never land back on the earth, and would instead orbit at a fixed height above the ground. Through this in-principle experiment it became clear to him that gravity was responsible both for things falling to earth and for maintaining the moon in its orbit around the earth.)

      Reply

  57. I was highly anticipating this article and was not at all disappointed—many thanks!

    Caught a few minor typos:

    —At the very end of the paragraph beginning “At the other extreme” (next to Fig. 4), I think “Figure 5” should be “Figure 4”.

    —In the first paragraph under “An Observer Who Views the Higgs As Moving Up,” you twice write “has” where you mean to write “as”: “she views the Higgs *has* having non-zero momentum, and similarly views the photons *has* having unequal…”

    —In the list before the final paragraph, you write:

    “compute the mass of the system of two photons (*their* invariant mass, in technical jargon)”

    If I’m not mistaken, “their” should instead be “its” (or perhaps even the uglier but completely unambiguous “the system’s”). Earlier you do such a nice job of stressing the distinction between total system mass and sum-of-the-masses-of-the-system’s-parts, and so I was a bit confused when I got to this point.

    Reply

  58. Matt, I thought you were going to add a section on “force” to this article? For me personally, relativistic force was far more confusing than relativistic mass and isn’t that well explained in most physics books.

    Reply

    1. Well — force will have to be dealt with at some point. But this isn’t quite the right place for it, I think. The concept of “force” is indeed a bit complicated in relativity and it is not often needed in particle physics — energy-based arguments are often sufficient.

      Reply

      1. Yes, I see your point. But still, electric and magnetic fields are essential in accelerating particles to the required energies at the LHC, and there are many electrical engineers reading your blog that probably aren’t aware of how relativity relates these two forces 😉

        Reply

  59. This is my first time commenting in your site so I would like to start thanking you for the great educational content you are providing here. I find your explanations quite clear but I would like to ask if you could provide some insight about how we got the geometrical interpretation of the relation between E, m, and p in the first place. I understood that you are simplfying things since the correct geometry is not euclidean but I guess the question still hold.

    Reply

    1. Well — on the one hand, physicists often take an algebraic formula and making it visualizable using geometry. Its a way of building one’s intuition for how the formulas work. Generally, such tricks do not have intrinsic significance, and certainly that is the case here for my use of the Pythagorean formulas. In particular, the Pythagorean intuition would not work very well for the complete set of relativistic equations one encounters as an expert.

      The non-Euclidean geometry, however, has deeper significance. It turns out that ALL of Einstein’s relativistic equations are consistent with the symmetries of hyperbolic geometry. This wasn’t instantly of obvious importance; mathematicians pointed it out very quickly, however. In retrospect, it is the easiest way to understand why the formulas take the form that they do.

      Reply

  60. “But quarks interact with electrons rather weakly, so electrons can easily fly free of quarks — and this is why electrons in atoms are found orbiting at a relatively great distance from the protons and neutrons that make up the tiny atomic nuclei.”

    1. How do you characterize the “relatively great distance” between the electrons and the neclei?

    2. With respect to the “order of nature” would you say that the positively charged proton (stabilized momentum wise by the neutron) “created” the electron to further stabilize the system and create the “final” state, the atom?

    3. More general question would be, is the pattern in nature, particle physics, that suggests a particular order of creation (of particles) driven by one particular interaction, quantum field?

    4. Is correct to say that the fundamental definition of quantum field interactions is the dissipation of “free” energy from a space of high density to a space of lower density (and visa versa)?

    5. Given space is proportional the velocity (motion-energy) and time (change of energy from one form to another?), is correct to say that space (the three dimensional space that we see all around us, including us) had to been created by an “action” outside the system? In other words, is the singularity a stable phase (quite happy to stay in that particular state until some external action “disturbs” it and boom, the Big Bang) or is it an unstable transition phase between two manifolds, or “something else”?

    Reply

    1. Oaktree: most of your questions really aren’t relevant to this article. For the benefit of future readers, please try to put your questions as a comment to an appropriate article whenever possible.

      1) The electrons in a helium atom are on average more than 50,000 times further away from the helium nucleus than the radius of that nucleus itself. By comparison, the earth is only 93 times further away from the sun than the sun’s radius.

      2) “positively-charged proton (stabilized momentum-wise by the neutron)” — this does not make sense to me. There is no sense in which a proton is stabilized momentum-wise by a neutron — indeed I have no idea what you could mean by this. And no, protons do not create electrons; they are lucky to find them. Some parts of the cosmos contain protons and electrons wandering on their own.

      3) In the early universe all particles that we know of were created, in abundance, due to the hot temperature of the Big Bang. That’s how there came to be so many particles. We do not know why the Big Bang happened and we don’t know how it ended up being hot. A tiny asymmetry between matter and anti-matter resulted in the current cold world having mainly protons and neutrons and electrons, along with photons and some neutrinos and anti-neutrinos, and something else that makes up the dark matter of the universe, and maybe some other things we don’t know about.

      4) No. Not even close. Where did you get that idea, if I may ask?

      5) ” Given space is proportional the velocity (motion-energy) and time (change of energy from one form to another?)”

      That’s really not “given”. I think you are trying to use the fact that velocity is a distance divided by a time interval, but “space” and “distance” are different things. Space is the three-dimensional world where things happen. Distance is a length between two points in space. You don’t want to confuse them. Similarly, time is the dimension that governs how things change, but a time interval is a “length” between two points in time. So velocity is not space divided by time; it is a distance divided by a time interval, not the same thing at all.

      “is the singularity a stable phase (quite happy to stay in that particular state until some external action “disturbs” it and boom, the Big Bang) or is it an unstable transition phase between two manifolds, or “something else”?”

      Almost certainly there isn’t a true singularity. The singularity (which is a place where the curvature of space-time becomes infinite) is probably just a place where Einstein’s equations for gravity aren’t accurate anymore and something else has to replace them, just as Newton’s equations aren’t accurate when you try to understand black holes. Since we don’t know what replaces Einstein’s equations near the (probably-not-a-)singularity, we don’t know the answer to your question.

      Reply

      1. Thank you for the responses. My question on the definition of a quantum field stems from my inability to visualize the concepts of energy-space-time. [ delta-E x delta-T >/= h/(2 x pi) ] I also am aware that the time Δt in the uncertainty relation is the time during which the system exists unperturbed. This explanation of the energy-time uncertainty principle is gave me the idea of how did the fundamental field was created to answer to everything we see and measure now.

        I do not believe in the theory of nothingness and I do need to see the equations, thank you. I do believe energy is fundamental of the three and in some elegant simple mechanism created space and time. I cannot visualize what energy is but, as you so brilliantly described in numerous lectures, I know when unleashed it creates wonders throw the forces it creates down the path of lower and lower “temperature”, motions.

        I interpret the energy-time uncertainty principle as the first change to occur, from a point of maximum energy (maximum energy density) is density itself. Even before space develops there must be a splitting, an “asymmetric breaking of” a single quantity, energy density. This first change creates direction, time, and hence space. Space, in my mind, could be the necessary outcome of having a variation(s) of energy densities. So, from the very beginning a field is created (the variation of energy densities) to define two “particles”, two states of energy. Like the living cell, as it continues to split the more interactions are created until enough diversity exists to create the forces we can see the effects of today.

        Energy density, temperature, must be the first single quantity in nature. If so, where it came from and/or how it came to be is and will remain a mystery we will never deduce. Some people, including scientists, may want to label it as God, some will try am make up mathematical relationships to remove the need for this “creation” and call it the Theory of Nothingness or M-Theory. I am still searching and some one can answer this question before my days are done.

        Reply

  61. To our dear master and teacher matt. : Allow me to remind you of 2 previously mentioned points :
    1- What is mass physically ? electron is 10^-30 kilograms ……..of what ? our body include one kilogram of electrons ! what does that mean ?
    2- Neutron decay – stability question.
    THANKS OUR DEAR INSTRUCTOR.
    best wishes , we enjoy this stupendous website very much , this is my sincere feeling indeed.

    Reply

  62. To Carl : I do not agree that we get the REAL properties from our real observations , in the ex. of matt. we got three packages of properties , which one is the real ? as i said we got our illusion of 3 packages from which the real is unknown , i mean what is the independent real properties ( in this and all similar cases ) of that higgs ? as far as i know — which is very modest — no real properties can be known unless we have absolute F.O.R. so every thing we OBSERVE is not but our calculations from a certain F.O.R.which represent our knowledge not the real thing. so real properties are in principle unknowable .
    This is my logical reflection , correct me please if i messed it up.
    n.b. : in the ex. matt.gave if the observer is the one who is moving thus he have the momentum , i cant grasp how his movement is assumed at rest and it was given to the higgs which is at rest as assumed! this is relativity , i know , but again i speak about real properties not observed ones…………..am i justified if i say : unknowable are the real?
    thanks

    Reply

    1. aa.sh: Carl is correct. Movement is a relative term. This in fact stems not from Einstein but from Galileo and Newton; for both Galileo and Newton, there is no meaning to saying “this object is at rest”. There is only “this object is at rest relative to this observer.” That is the first principle of relativity; see http://profmattstrassler.com/articles-and-posts/relativity-space-astronomy-and-cosmology/the-first-principle-of-relativity/

      Aristotle believed there was meaning to saying “this object is at rest”. Part of the history of physics was realizing that Aristotle was wrong.

      Indeed, this is one of the points of this article, but I can see from your question that I should have brought it out explicitly. Marie, Chris and Peter are equally good observers. The laws of nature work for all three of them. There is no special set of observers who are at rest, relative to whom the rest of us are moving. And there is no meaning to saying “This Higgs particle is at rest” and “This one is not” without reference to a particular observer.

      You can try to object, but the proof is in the experiments; there’s no sign that there is any meaning to saying “this object is at rest”.

      That said, there is, curiously, a subtlety here. You can be at rest relative to the very distant galaxies; the universe as a whole does have a preferred set of observers. But you cannot tell this if you do an experiment in a closed room. You can only tell if you are able to look outward, and see the universe. This is consistent with a precise reading of Galileo’s relativity and Einstein’s relativity principles.

      Reply

      1. That last paragraph confuses me. I thought the galaxies were all moving relative to one another; so how can one be at rest with respect to all the very distant galaxies?

        Reply

    2. When you assume there are some REAL properties, you implicitly assume there is an absolute frame of reference. At least this is how I understand it. If I say about a movie that is bad and you say it’s good, is there an absolute reference to give us the REAL value of that movie?

      Reply

      1. / is there an absolute reference to give us the REAL value of that movie?/–
        Yes, it is called, Logos ( λόγος).

        Reply

  63. There is one point i miss , you said momentum is related to speed , direction and mass , the heavy have more momentum than the light within same speed , now how mass-less photons could have momentum while it is light to the zero degree ??

    Reply

    1. Momentum of photons is different. It’s related to direction and frequency (well, p=hbar*k, where hbar is the reduced Planck’s constant and k is the wave equation, and that k has the information about direction and frequency). It confused me too, for quite a while.

      Reply

      1. Carl ; it isn’t really different. It’s just a bit confusing at first. Look at the first few figures of this article, with the various triangles; you’ll see that for a massive particle, speed grows when momentum grows, while for a massless particle the speed is always c no matter how large the momentum is.

        Reply

    2. Thank you for this question; I should have explained this better too. Look back at the triangles in the first few figures of this article… there you can see what I said was consistent. But I should have reminded readers of this.

      Reply

  64. As someone has already pointed it out, in general relativity energy is not conserved except in very special circunstances. Although I believe it’s not your point discussing general relativity and therefore your omission is justifiable. To clarify if I may, the conservation of energy appears when things are invariant in time. But if things are different at different times, like in a universe that started in the big bang and expands, then there will be no energy conserved when you look at the complete universe. But even in general relativity energy is conserved locally and that’s the reason why it is ok to talk about energy conservation in the LHC. Only globally the subleties arise.

    Reply

    1. I agree. There is always the question of when to bring up this subtlety, and other subtleties with general relativity or with dealing with the universe as a whole. The best approach tends to be to try to forget about the universe as a whole until you understand how things work in a small portion of the universe, say within the solar system or within a terrestrial laboratory; then you’re in a position to understand why looking globally across the whole universe introduces many subtleties.

      Reply

  65. “But the mass of any object is something that all observers will agree on.”

    “Instead, the mass of a physical system, which all observers agree on, is determined by its energy and momentum, …”

    Here’s where you lost me (and it’s what prompted my previous question). The first statement appears to be talking about “rest mass” but the second statement appears to be talking about “relativistic mass” (I apologize for using the older terminology, but it seems more clear in this context). I’m sure it’s just confusion on my part, but I’m simply not following what is meant by “mass” at various points in this article.

    Reply

    1. Ah — I am sorry I have confused you. I can see how I haven’t phrased it well. What I meant was that the mass of a physical system is **known** if you know its energy and momentum, because

      (mass_system c^2)^2 = E_system^2 – (p_system c)^2

      But the whole point is that if you speed up the system, its E and its p both increase, such that mass_system does not change.

      So I am *always* talking about the mass = rest mass =invariant mass —- called “rest” because at rest E = mc^2, and invariant because no matter what E and p are, the mass is always the same. And we saw that for Marie, Peter and Chris; they all say the (invariant!) mass of the system is 126 GeV/c^2, even though they measure very different energies for the system.

      Does that answer your question clearly enough? I will change the wording in the article to make this clearer and I thank you for your question.

      Reply

      1. I’m having a problem understanding the system rest mass.The equation says the system itself has mass, even though the individual photons do not. How does this system mass manifest itself (i.e. how can we measure it)? How can the two photons together, even if they be at opposite ends of the universe, somehow exhibit mass-like properties?

        Reply

        1. Good question, and not so easy to answer.

          It is not easy to answer because you ask the right question: how can we measure the mass of the two-photon system? And the answer is that it isn’t easy to do it with any simple experiment, because the two photons are not attached to each other, making it difficult to do any experiment on them collectively. If the two photons are at opposite ends of the universe, the fact that it is true that they collectively have a mass isn’t something with important consequences; it is true, but not interesting.

          But suppose I put the two photons in a box with mirrors at the two ends: | | so that the photons bounce back and forth again and again. The system of the two photons will always have the same invariant mass as long as I maintain the symmetry between them, so that they are always going in opposite directions and always with the same energy. Now if I try to move the box I will discover that indeed that the mass of the box includes not only the mass of the box when it is empty but also the mass of the two photon system as well.

          The answer is a little bit contrived, but it is, nevertheless, correct. And similar answers are important in understanding the mass of the proton, which is partly due to massless gluons and very lightweight quarks moving around in the proton at high speed.

          Reply

      2. “Now if I try to move the box I will discover that indeed that the mass of the box includes not only the mass of the box when it is empty but also the mass of the two photon system as well.”

        Regarding the above sentence, I would like to ask: Are you saying that the two photons contribute not *twice* their individual *energies* divided by c^2 to the total mass of the box + 2 photons, but the 2 photon *system mass* as defined by Equation 1′?

        Thanks.

        Reply

  66. By “invariant mass”, I presume you are talking about the “rest mass”, i. e., the mass the object would have if it were not moving. Correct? And the “mass” you write about in the “Where we are now” section is the “invariant mass”. I might suggest that you occasionally, in this article, reconnect with the fact that your use of mass is the “rest mass”, just because the “mass increases as you approach the speed of light” idea is so ingrained into many of us who’ve read up on special relativity …

    Reply

    1. Thank you for your question. I need to be very careful about how I make these statements, because, as you say, many people have read that mass increases with speed, which was a point of view that needs to be expelled from the lexicon (otherwise it makes no sense that massless particles travel at the speed of light, or to say that photons are massless). So thank you for this suggestion; I will indeed sprinkle some reminders around, and occasional links to the little article I’m writing that explains why I use “mass”=”invariant mass”=”rest mass” and *never* us “relativistic mass”=”energy divided by c-squared”, which I (and all of my theory colleagues) simply call “energy divided by c-squared”.

      Reply

  67. This may be a silly question — relative to the expert — but i always try to understand the meaning not only the book keeping , now , the higgs are really at rest , 2 observers are really moving , well ..what you are describing is the illusions the observers calculate not the real properties of the 3 higgs which are REALLY AT REST ! my question is : how can we get the real properties from our unreal illusions ?
    Forgive my ignorance , but remember ; i am NOT a physicist .

    Reply

    1. You say that the Higgs is “really” at rest. That’s not a useful statement with regards to Einstein’s theory of Relativity. The observers are all stationary (from their own perspective), and the Higgs and other observers are all moving. If the observers are on Earth then the Higgs is moving with the Earth, and an observer in space would see it moving quite rapidly indeed. There is no fixed, universal frame of reference.*

      So we get the real properties from our real observations. There are no unreal illusions involved.

      *I should note that the Lorentz-Poincaré “ether” theory metaphysically allows for a unique, absolute rest frame, but that this frame is empirically undetectable and thus irrelevant. The discussion is simpler without it, and it can’t change anything, so we leave it out.

      Reply

  68. Is it true that in general energy is not conserved in general relativity? What is the subtlety there?

    Reply

    1. Even in general relativity, energy is conserved in small regions where gravity is not too rapidly changing — for instance, in any particle physics collision, terrestrial experiment, or satellite launch. But computing total energy in very large regions across which there is a significant amount of curved space and time can sometimes become ill-defined.

      Experts in general relativity can tell you better than I can what you can and can’t do in universes of various shapes. We obviously don’t know much about the universe as a whole — we only know something about the patch that we can see, and even for that patch there is still much to learn.

      Reply

      1. But then energy conservation is an approximation – an approximation accurate to many, many, digits of precision? In the derivation of energy conservation from Noether’s theorem, is it that time-invariance (the symmetry that leads to the conservation) is lost with GR because the system is no longer isolated and even if net rate of interaction with the “outside” is 0, its timecourse may not always be 0? I can’t say I understand even a little how energy can become ill-defined. Is it that energy of a “closed” system is undefined since, with GR, there is no closed system? Nor, for that matter, do I understand what curved time means. I guess these aren’t questions relevant specifically to this article, where only local (gravity-change minus) interactions are looked at?

        Reply

  69. Does it make sense to talk about the whole Universe as a system of objects, e.g. to try to determine if it is a closed or an open system?

    Reply

  70. Thanks for such a clear exposition.

    Some of your readers might like to read “Energy, the Subtle Concept: The discovery of Feynman’s blocks from Leibniz to Einstein” by Jennifer Coopersmith. It gives a very clear account of the idea of energy and is pitched at about the level of your article.

    Reply

  71. What role does oscillation have in the sub-atomic structure ? if there were none does our world be different? is it an epiphenomena without role….a byproduct of something ?

    Reply

  72. Thank you Prof., for an excellent review that scientists outside physics world could follow.
    You have not discussed about conservation of angular momentum. Is there a symmetry associated with it?
    Thanks for taking your valuable time.

    Reply

    1. Yes, it is the symmetry associated with the fact that an experiment done in any orientation (at least far out in space, in a region where gravity is negligible, or on earth but so quickly that gravity has no substantial effect) will yield the same result. The technical term is “invariance of the laws of nature under rotations”.

      Reply

  73. It was interesting to read your elegant presentation here with an eye toward what superluminal neutrinos would have done to the discussion …

    I posted a previous comment which unfortunately never made it out of the “awaiting moderation” stage; since it involved neutrinos and I have introduced the topic here (admittedly through my own sleight of hand), I’ll ask a shortened version here:

    When neutrinos change mass generations (what’s the correct term for this?) in flight, since each type of neutrino has a slightly different mass, they must be trading mass-energy for motion-energy (to use your terms) as they travel — so their velocity actually changes as they fly. Is this thinking correct?

    Is anything known about how *often* they change generational types as they move? Or is this really more a question of the neutrino being in some sort of superpositional state of all three types at once?

    Reply

    1. Sorry that I never got to that question; I thought I’d answered that one, but I must have answered a related one from someone else.

      “changing mass generations” is called “oscillation”; I wrote some things about it here http://profmattstrassler.com/articles-and-posts/particle-physics-basics/neutrinos/neutrino-types-and-neutrino-oscillations/

      which answers your last questions — it is superposition that is involved, and as for how often they “oscillate”, yes, we are in the process of filling in the last gaps in our knowledge now. I still haven’t had time to write about this.

      As for your first question, the answer is yes; the velocities for the different states of which the neutrino is a superposition are very, very slightly different. It is worth calculating how different they are from the speed of light, and how different they are from each other… you will find that it takes a very long time for them to become macroscopically distant from one another. To understand why oscillations can continue despite these slightly different speeds is an extremely subtle issue that I can’t answer in a comment (and people still debate the best way to handle this subtlety in a theoretical calculation, see for instance http://arxiv.org/abs/arXiv:1006.2372.) Maybe someday I’ll try to address this, but I need to make sure I have the subtleties right in my own head before I try to think about how to explain it to a non-expert…

      Reply

      1. Matt, I have a question about those oscillations. In theory, if there is another set of electrically neutral (nearly) stable particles (such as dark matter, but not necessarily), they could oscillate such like neutrinos or this is something that only neutrinos can do?

        Reply

        1. Oscillation can indeed happen in other contexts; this happens for certain hadrons, in particular neutral Kaons and Anti-Kaons mix, as do neutral B mesons and anti-mesons. More broadly, it is a very general phenomenon in quantum mechanics.

          Reply

      2. In light of neutrino oscillations, could one say quantum entanglement is synonymous to the gravitational field? I one can assume the gravitational field is the fundamental field upon which every other field is derived from, then would it not be the likely candidate to cause the neutrino oscillations. The neutrinos are the lightest of the known fermions so they would be most interactive to the very weak gravitational field.

        Maybe a better question would be is the Higgs field synonymous with the gravitational filed?

        Reply

  74. The truth i mean is that 🙁 from inside the universe we cannot in principle know ” every thing “) , for some this may be a proposal under investigation , for me it is a solid ,sound logical truth.
    We cannot just spend our whole life to its end seeking without finding , at some point after we spend lot of time seeking we reach a conclusion , or otherwise we wasted our life in vain , in total void where no meaning , no end goal , no destiny exists , science , physics and biology in particular are our main windows to look at truth but on the condition that no prejudice , no arrogance , no vanity enters our labs.
    In origins sciences –physics and biology — it is very sad fact that we find that dark trio , what i like much in the discourses of matt. is his neutrality which is very much appreciated.

    Reply

  75. “It has been known for about twenty years that for a low Higgs mass relative to the top quark mass, the quartic Higgs self-coupling runs at high energy towards lower values. At some point it would turn negative indicating that the vacuum is unstable. In other words the universe could in theory spontaneously explode at some point releasing huge amounts of energy as it fell into a more stable lower energy vacuum state. This catastrophe would spread across the universe at the speed of light in an unstoppable wave of heat that would destroy everything in its path. Happily the universe has survived a very long time without such mishaps so this can’t be part of reality, or can it?” … Philip Gibbs

    Reply

    1. Getting your physics from Mr. Gibbs is risky. What he leaves out, in this discussion, is the fact that there are several important assumptions that go into the statement that “at some point [the quartic Higgs coupling] would turn negative indicating that the vacuum is unstable”; we simply do not know this, because other particles of which we are currently unaware could change this conclusion. The other thing he leaves out is that “at some point” is likely to be trillions, or trillions of trillions, or trillions of trillions of trillions of years from now. So he’s scaring you, or at least convincing you, for nothing.

      Reply

      1. Thank you for that. That was very valuable info, the part that .. “we simply do not know this, because other particles of which we are currently unaware could change this conclusion.”

        This very fact is should be, if it is not already, raising red flags over at CERN with regards to the actual mass-energy of the Higgs boson. We see a small bump aw about 125 GeV but the sigmas are still way too low for any concrete validation, in my opinion anyway. And this because it could very be some other particle, maybe even a non-SM Higgs.

        So my question is could the SM Higgs boson resonance be hiding under the Z boson resonance peak? And what we see is the combined energy of both “particles”. I guess my basic question is fi we are getting closer and closer to the region of unstable vacuum levels what will be the features to differentiate between two or more Higgs boson, instead of assuming and fixating on one?

        This line of questioning has been with me for a long time and have been asking to any physicist who would be willing to answer me. I have some idea and what is preventing me from visualizing the potential mechanism for the quanta particle (fundamental field geometries) is Pauli exclusion principle. Why can bosons occupy the same space and fermions cannot? Is Pauli principle giving us clues as to the make up of the creation (coalescing of) the first field. (gravitational field?).

        Reply

  76. Prof please answer my question. Are bubbles rising up from God’s kettle only to burst when we reach the surface of total vacuum, VEV = some constant.

    I don’t believe we will reach maximum entropy because there will be point before that, that the vacuum will go unstable again and the universe will be succumbed by a massive wave of fire. (i.e. the Higgs field lowering to about 120 – 125 GeV). Then the bubbles burst.

    Reply

    1. You are asking questions about things that (a) are not known, and (b) will not affect the universe anytime in your lifetime or most likely the lifetime of any star you can see in the sky. Maybe some day we will know the answer; right now, we do not.

      Reply

  77. TO WHOM IT MAY CONCERN :
    RE. : Particle / anti-particle annihilation post……comments of 30 march.
    THANKS PRONOEIN , THANKS PROFESSOR STRASSLER , you just said exactly what in all my comments i wanted to clarify , <<>> so why some readers accused me of trolling ? now you know that aa.sh. is right in saying that physics per se does not tell the whole story , so tell the tales perhaps they will reflect.
    N.B.; it was my obligation to defend truth that i was obliged to write this.
    thanks for every one…….no hard feelings.
    aabed with full respect.

    Reply

    1. “Most people, including ourselves, live in a world of relative ignorance. We are even comfortable with that ignorance, because it is all we know. When we first start facing truth, the process may be frightening, and many people run back to their old lives. But if you continue to seek truth, you will eventually be able to handle it better. In fact, you want more! It’s true that many people around you now may think you are weird or even a danger to society, but you don’t care. Once you’ve tasted the truth, you won’t ever want to go back to being ignorant”

      Socrates (469 – 399 BC)

      Reply

    2. To be fair in all directions; you are not the only defender of truth. There are people who disagree with you who also believe themselves “defenders of truth”. We are at the edges of knowledge and understanding in this conversation, where the truth is not known.

      Reply

    3. “now you know that aa.sh. is right in saying that physics per se does not tell the whole story”

      You present no evidence to support your (vague, unspecific and essentially meaningless) claim, nor the clear implication that “something else tells the whole story”.

      The entire history of science – not just physics, but the results of the practice of the scientific method in every area of human knowledge – is the process of natural explanations satisfactorily replacing unsubstantiated magical explanations.

      There are no examples of the opposite occurring. None.

      There is no reason to suppose that this trend will not continue.

      “Physics” is not a static object, it is a process of exploration and a growing body of internally consistent knowledge. To say, “physics per se does not tell the whole story” is like saying “eggs are not chickens”. That does not mean that chickens must come from spoons.

      I think every human being deserves respect – but not every claim or argument made deserves automatic respect. There is no there, there, and repeating the same claim over and over without any support does not make it respectful, in my opinion. YMMV.

      Reply

  78. Hi ! Thanks for your very good articles !

    I have a simple and perhaps “stupid” question..(ok stupid questions doesn’t exist…)
    How do physicists found conservations/symmetry laws ? By experiments only ?

    Reply

    1. That’s a very complex question, in fact.

      How do physicists learn anything? Here is a cartoon: Experiments give data; the data is analyzed and an attempt is made to interpret it; patterns are noticed; the possibility of a conservation law in the relevant experiments is suggested by someone; further experiments to test the idea are suggested; perhaps they tentatively confirm the result; the possibility that the conservation law might apply more broadly is suggested, and more experiments are proposed; these are carried out, with success or failure, and debate ensues as to whether the conservation law is right or wrong; more experiments are proposed and other previous experiments are reinterpreted; theoretical attempts are made to explain the conservation law and relate it to other physical phenomena; perhaps mathematicians get involved — and over a period of decades it becomes clear whether or not the proposed conservation law is badly invalid, approximately valid or exactly valid, whether it is general or applies only in certain situations, what other scientific principles it is related to and how it fits in with them, and how to understand it from a theoretical point of view, both mathematically and perhaps conceptually.

      What I really mean by this is that to answer your question, you’d have to read a book — a long one — packed with scientific history, about all the steps and missteps involved in allowing experimental and theoretical physicists to come to such a spectacular scientific conclusion as a conservation law. Maybe such a book exists for the conservation of energy; it would be quite fascinating to read. There’s a lot of history there that I am certain that I don’t know.

      Reply

  79. If particles gain their masses via interaction through the Higgs field, wouldn’t that mean that mass energy is really a form of “relationship energy” (aka potential energy)? Remove the Higgs field from the universe and this relationship – and the associate energy – vanishes.

    Reply

    1. Yes, you can view it that way. But it’s a special type, since (the Higgs field being everywhere) a particle carries it everywhere it goes.

      Note also that the relationship doesn’t entirely disappear even if the Higgs field is on average zero. The top quark mass arises through a basic interaction in the equations between the Higgs field and the top quark field. The same interaction produces some energy when a Higgs particle and a top quark (ripples in their respective fields) pass near each other.

      When we actually work with the equations, we don’t really have to worry about these definitions. Typically physicists have multiple ways of thinking that are calculationally equivalent and that they are quite happy to switch between; the more you have, the more flexible you are. What really matters in the end is how you calculate; physics is, at heart, about prediction. Whether it is better to think about things the way you suggest, or not, depends on what you are calculating; it is up to you to organize the calculation in whatever way is most convenient.

      Reply

  80. Professor Strassler,

    I just wanted to say thank you for this article, which was very clear and informative. I have never heard relativity explained in the context of trigonometry before, and it personally makes a lot more sense to me now. I also would very much appreciate you taking the time to explain it in terms of hyperbolic trigonometry, as you suggested you might at some point.

    Also, I appreciate the way you handled the discussion in the comments above regarding different philosophical approaches one can legitimately take to science, while still being true to science. Too often these days are we seeing high profile scientists who at best want to downplay the role philosophy has in science, and at worst claim that it is “dead”. I myself am a scientist who thinks that such philosophical questions as to why the Universe exists at all or other meta-scientific questions (as you put it) are indeed interesting and relevant, and are no less so simply by virtue of lying outside the realm of science.

    Reply

  81. Thanks so much for taking the time to write these educational articles. I’ve also been reading the Feynman lectures, and IMO your educational pieces are every bit as engaging and accessible while covering much more advanced material in most cases.

    Reply

  82. One question I had for a bit:
    A massless particle has v=c, m=0, and E=(p)(c).
    E^2=(mvc)^2+(mc^2)^2
    What’s the velocity? Solve for v.
    v=1/(c*m)*sqrt(e^2-c^4*m^2)
    If the mass is set to 0, there’s a divide-by-zero error. If we try to limit it to 0, there’s still a divide-by-zero error. The limit of the derivatives of the numerator and denominator is 0. So v should be 0. E must be 0, since mass is 0.

    Of course this confusion comes from thinking that p=mv. For a photon, p=hbar*k, where k is the wave vector. There’s a danger in trusting everything you learn in basic physics. Some very important details get left out.

    Reply

  83. To Casey : I do not have a hidden agenda , all my statements ( without being ” provocative” ) aims at main goal : to clarify that existence / ontology is not mere physical realm as atheists claim.
    A website of science …..of physics in particular can never be isolated from a worldview which is here naive realism.
    This is free conversation website so every reader have the full right to discuss all related points within the scope of science /philosophy.
    As i see a trend to narrow that scope i hereby declare that i will quit my right to share in this conversations since confining ( honest interest ) in a particular biased group is an insult to all others.
    Thank you matt. and sorry for that gross misunderstanding.

    Reply

    1. Personally I do not intend to narrow the scope of the website. I aim to maintain a good balance between different goals, in order to serve many different types of readers. I would hope my readers would try to respect the needs of others with different goals, and to be patient; you can skip over their comments if you’re not interested in them. And you don’t need to defend me; I can shut off a conversation whenever I want to (and sometimes I do.)

      Reply

  84. I am probably stating the obvious here: Since mass converts to energy and conservation of energy is all that really counts – does it not follow that mass is simply another form of energy?
    I am waiting for that matter replicator …. convert energy back to mass! 😉

    Reply

    1. First of all, we convert energy back to mass all the time — that’s how we make Higgs particles (and top quarks and W particles and Z particles) at machines like the Large Hadron Collider! This is described toward the end of my particle/anti-particle annihilation article, http://profmattstrassler.com/articles-and-posts/particle-physics-basics/particleanti-particle-annihilation/

      As for whether “mass is a form of energy” — you can certainly take that point of view, and I personally do. We’ll see better reasons for it soon, when I get to the mass of the proton and the stability of neutrons inside of atomic nuclei. But I don’t see anything in the equations that absolutely requires you to say it that way, and sometimes people object, so I don’t insist on it.

      Reply

  85. “■E2 = (mc2)2 , or in other words E=mc2 ,” (sorry superscripts did not copy correctly)
    What happened to the +/- in these square roots? Shouldn’t the answer be +/-E = +/-mc**2?
    I sort of understand the negative (potential) energy concept but thought there were no negative masses.

    Reply

    1. You are correct that there is an apparent ambiguity there. It turns out that if you work through the equations of quantum field theory, the ambiguity never actually arises; the mass of any well-defined particle is positive. If this were not the case, and the mass-energy of a particle were negative, then you could reduce the energy of a system by producing as many of these particles as possible, and empty space would be completely unstable. So in any universe where empty space is stable, all particles have positive (or zero) mass-energy.

      I think there’s an even better and more convincing answer but I can’t think of it now.

      Reply

  86. To Mr. powell : your grave mistake is your worldview as it was declared by your comment , you take it for granted that the universe is closed so physical realm is all of existence , this is the same worldview of THAT man with Ph.D and lots of papers !!! , well , let me ask : what is your independent absolute irrefutable proof of this ??
    There are many respectable thinkers who discussed this and the conclusion is : we cannot in principle prove this from inside the universe , so why are you so excited by my paraphysical realm ?
    learn brian……learn , and know that courtesy is appreciated.

    Reply

    1. To aa.sh: I’ve made no such claims regarding any such world view. I am an empiricist. I do not have proof that the physical universe is all that there is, nor do I necessarily believe that to be the case. My point is simply that Prof. Strassler is discussing physics here — a discipline that concerns itself with the epistemology of the natural world. There may well be things beyond this epistemology, but then these things are by definition outside the purview of physical theories; they are not — cannot — be addressed by science. If you are suggesting that there is evidence for the failure of a physical theory — in the empirical sense — on account of these alleged paraphysical aspects, then are they not actually just aspects of the physical world awaiting discovery? Perhaps aspects of the physical world that we do not yet have an understanding of? If so, then you have no disagreement from me. But a truly paraphysical phenomenon is one that is not only unknown in terms of physics — it is unknowable. So what I don’t understand is why you think you will find satisfaction here — on a science blog? I might believe that unicorns control my thoughts…but do you think this is the place to debate that? My world view is one based on evidence. There could well be other things in the universe, but I can’t test them and so I can’t know them. In any case, I don’t wish to interfere any further with your dialogue with Prof. Strassler. I hope you find what you are looking for.

      Reply

      1. I tend to sympathize with Brian’s thoughts, here… I’ve noticed that aa.sh has also posted in other topics on this site under the name Aabed Shami, which a quick google search shows to mean roughly “Worshipper from the Levant” in Arabic.
        All things considered, I think it’s fair to say that he’s probably not here mostly out of intellectual curiosity so much as to push a particular point of view or stir the pot. Whether that’s trolling or not, I can’t really say. But I think it’s perfectly normal for people with an honest interest in the content of the site to take umbrage at what appear to be intentionally provocative statements and questions.

        Reply

        1. I also sympathize with what Brian has replied, in several senses, though not all.

          To aa.sh: I think you are setting up a straw man (i.e., a fake target to shoot at that doesn’t really exist) and Hawking is indeed partly at fault. You’re trying to convince me (and Brian, it would appear, and many of my colleagues) of something of which we are already convinced; that science has its limited realm in which it does a fantastic job of describing the world, but beyond which it may not be applicable. Many of us have more humility about the limitations of science than Professor Hawking, who, though entitled to his point of view, has not swayed the scientific community as a whole. Nor will he, because his belief cannot be subjected to a scientific test. It will remain a matter of meta-scientific (a word I prefer to para-scientific) debate.

          Science can only be carried out when it is possible to design repeatable controlled experiments. I am sure that some aspects of consciousness — maybe many aspects — will be susceptible to scientific study. But I am not convinced that there will be a satisfactory scientific explanation for why we experience consciousness, rather than merely acting as though we do. Or that there will be an explanation as to why there is a universe at all. I do not see a scientific strategy to address these questions.

          I do think that understanding the limits of science properly is a role of any website on science. That is why I also am sympathetic to aa.sh’s concerns, and do not agree with Brian that these types of questions should not be raised at all on this site. Laypersons, especially, need to have the opportunity to raise issues concerning where science can and cannot, and should and should not, be applied.

          Casey: I don’t see the relevance of what someone’s name, or handle, means. I work with people from all across the world, some of whom have names similar to this one. Should someone’s name or handle, religious views or cultural background, philosophical bent or political views disqualify them from commenting on issues in science? The issue, it seems to me, is the pertinence and appropriateness of the comments themselves. The name behind the comment seems completely irrelevant to me.

          Reply

      2. Matt, I completely agree that one’s cultural, religious, political, philosophical, etc, etc views are irrelevant to the discussion, and didn’t mean to imply otherwise. My point was that it’s common in many forums for people trying to push a specific agenda or trolling to betray themselves with their handles. If you’re on an environmental/climate science blog and see a lot of provocative comments from someone with the handle “AlGoreStinks42,” it’s worth considering whether that person is really there for honest discussion or trying to build a fire.

        Reply

        1. Fair enough, but aa.sh has been on this site for a while, and I have seen no problematic agenda here. He’s not trying to show that science is a bunch of crap, scientists are idiots, and the empirical method is invalid; I would shut that down as a waste of energy. As far as I can tell, he’s trying to find holes in the reasoning of anyone who would claim that the success of science implies that the world is entirely physical, by arguing that the empirical method is incomplete, and that science cannot possible explain all aspects of the world. That’s a perfectly legitimate philosophical goal, as legitimate as that of people who would seek to establish the reverse.

          Reply

    2. I think the answer is much simpler, and it starts with Occam’s Razor – why invent complicated, supernatural explanations for what has perfectly satisfactory natural explanations?

      It is a matter of probabilities, not certainties:
      IF there is absolutely no evidence supporting claim X as an explanation for a range of phenomena;
      AND IF more and more of the observed phenomena within that range are explained without resort to X;
      THEN, even if X was considered plausible before simpler explanations existed for these phenomena, it is not only reasonable, but entirely prudent, to consider X extremely unlikely and unnecessary as an explanation, to the point that continuing to promote it is not reasonable at all.

      Adding to this is the fact that, in each and every previous case in which X was posited as the only possible and adequate explanation, natural explanations have proven not only possible but completely adequate to explain the phenomena, and there remains no rational reason to be deferential to continued claims that “X did it”.

      Calling X “paraphysical”, or “spiritual”, or “god’s hand”, or “mysterious”, doesn’t make it any more reasonable or worth being deferential to than calling it “turtles all the way down” or “aether”.

      Reply

  87. “Massless particles must travel at the speed limit; massive particles must travel below it.”

    I was trying to think if there were situations where massless particles were traveling at less than the speed of light.

    Would “Massless particles must travel at the speed limit [b]in vacuum[/b] be more accurate?

    Reply

    1. I like this question. The speed of light in a material is not c. Instead, it is c divided by the refractive index of the material. How can this be valid under the relativistic equations?

      Reply

  88. This is pure gold Matt. One thing I didnt get though, how did we get this relation v/c=sin(alpha)

    Reply

      1. Thx for the answer. How did we get then this relation v/c = p c/ E? This is actually what I wanted to ask in the first place, it appears that I’ve got distracted and posted the wrong equation -facepalm-

        Reply

  89. Think total ……global not local , my ” energy ” is very well understood as an action , a directing , a morphogenesis , a generating…….
    What i aim at is to show that science DOES NOT KNOW every thing , the overall realm is much more greater and broader than physical realm , or else science will be trapped in the greatest delusion of self worshiping , we have a very clear example in THAT man who is a very good example of ultimate arrogance.
    Dear friend ; you just cannot talk physics without philosophy …. 2 faces , same coin.
    thanks

    Reply

    1. But this is a truism — on this point we are not arguing opposite sides at all. Of COURSE science does not know everything. Science can only answer those questions for which a repeatable, controlled experiment can be designed. Designing controlled and repeatable experiments to get to the heart of what consciousness is lies beyond the state of the art, and might never be possible. Certainly we don’t understand it *yet*.

      You are welcome to use your version of the word “energy” whenever you like, but don’t *confuse* it with a physicist’s version. The statement that *energy is conserved* applies ***only*** to the physicist’s version. The fact that we don’t understand what you are calling “energy”, and that your version of it isn’t conserved, does not imply that scientists do not understand the version that physicists define for their use.

      In short; I’m not saying that you’re wrong, only that you’re phrasing your point badly, and creating a mess instead of clarity, by mixing up two very different notions of energy, one of them conserved, the other not.

      Reply

  90. Troll somewhere else aa.sh. There is an enlightening discussion going on here amongst those of us who are actually interested in learning something about the natural world. By the way, I’m amused by your tactics: 1) try to paint Prof. Strassler into a corner by pointing out alleged logical/physical errors in his exposition (thereby really only succeeding in betraying your own ignorance) 2) when this fails miserably, drop your paraphysical bombshell that you’ve not in any way succeeded in establishing a need for, with the caveat that you simply believe it to be true. Let’s check this nonsense at the door.

    Reply

    1. I disagree, Brian; please be polite. Mr. aa.sh, if you listen to him closely, always asks sensible questions. And he listens to the answers; he is honestly trying to understand, even if his language is not that of a physicist. I do get nutcases on this site, but he is most definitely not one of them. And many of my readers share his questions.

      Reply

      1. My apologies. I have a quick trigger finger sometimes; I’ll mind my manners in the future.

        Reply

  91. The point is :
    From where the ” energy ” which is directing the physical energy come ?
    No other source but an extra-physical one……..period.

    Reply

    1. >>From where the ” energy ” which is directing the physical energy come ?”

      The “energy” you put in quotes is NOT ENERGY.

      >>”No other source but an extra-physical one……..period.”

      Agreed. But it isn’t *energy*. Not in a physics conversation. If you write a sentence in which you call two different things by the same name, you will confuse everyone around you (and yourself.) Physicists’ “energy” is not the same thing as “action of the will”, which is what you are calling “energy”.

      Noether’s theorem says physical energy is conserved. It says NOTHING about action of the will, or other things that you may colloquially, or philosophically, or whimsically call “energy”.

      Reply

  92. Please note that i wrote ( the ultimate source…..) which is decision / consciousness ……then you agree that there are cases where until we understand consciousness energy is not conserved……this is a deduction not a quotation.

    Reply

    1. We have no evidence that the experience of consciousness itself uses energy. The physical processes of consciousness (thinking, for instance, and processing sensory data) most certainly use energy — physicists’ energy — which is part of why it is becomes hard to think when you have not eaten in days.

      Reply

      1. However, what you are doing is pushing the question of conservation of energy into the most complicated physical system known — the brain and biology of a human.

        Physicists make progress by studying simpler systems first. I do not know the equations for a human, therefore I am not sure I know what the energy E is, and it is possible that I am missing something. That does not mean that I do not understand energy, and its conservation, in those contexts where I *do* know the equations.

        It is a logical error to suggest that because there is something very complicated that you do not understand, you do not understand anything at all.

        Reply

  93. Now we reached the aim of my dialog …
    Matt. : you ASSUMED that the energy stored in the body is the ultimate source of the body / earth movement , that is a very big fallacy ( sorry but this is what i believe )!! that energy is diffused un-directed energy , we still in need of a directing something beyond the physical as we exhausted all resources of the physical….. i utterly and totally convinced that an immaterial paraphysical source is needed….i mean consciousness.
    To oaktree : just think of a physical mechanism that can generate equations and implement it in the physical , if yon cannot conceive one then THAT man you mentioned is utterly deluded……pity him.
    Even if vectors cancel each other , in reality there are a real action not zero.

    Reply

    1. No, it is not a fallacy; the movement of energy in and out of the body is a measurable quantity, subject to detailed scientific study. (“Calories” are units of energy; “burning fat” is about converting the energy stored in fat into your body’s motion energy.)

      You are making the classic error I alluded to early in this article; you are using the word “energy” in a way that it is not meant by physicists. I am using it precisely as physicists use it.

      If what you are asking is how you *decided* to move your body, that I have no answer for; scientists do not understand how conscious decisions are made. That does not affect my answer, however, to the question of where the energy (physicists’ “energy”, not your version of it) to carry out your decision came from.

      You must distinguish consciousness (which we do not understand) from the physical processes in the body (which we do understand rather well) that may follow from conscious decisions in the brain.

      Reply

    2. To aa. sh.: I think you are confusing momentum and energy. When you walk on Earth there is an equal and opposite reaction of the forces, plus some lost entropy, to enable you to walk. The resultant momentum change is zero, i.e. the zero here is the conservation of momentum. However, the energy spent by you and the Earth, plus some lost entropy, remains the same, hence the total energy of the universe remains the same, conservation of energy, thank God. 🙂

      As for “THAT man”, if you do some homework and find out who THAT man is you will find a genius and certainly not deluded and certainly doesn’t need your pity. Being a man of strong faith I refuse to abandon the concept of God, Dr Hawking elected to let go and put his faith in the mortals M-Theory. Where I disagree with Dr Hawking and where Prof Strassler eluded to, is that we don’t have all the physics yet and it is impossible to experimentally test the M-Theory.

      To Prof Strassler: I wonder if you notice my reply on my continued search for E, above? Allow me to be bold and ask, is E the universal coupling of everything? And I am referring to the same coupling the Higgs boson makes with some (or all) particles. I ask this question based on recent experiments that confirm the existence of quantum entanglement. Is E the result of everything point entangled to every other point in spacetime? I am somewhat familiar with the Theory of Nothingness and I have heard a theoretical physicist say (no names, but his teaches in Phoenix, :-)) that the total energy of the universe is zero. But what I am saying is it can never be zero and never was zero. So going back to the Big Bang Theory, this energy must have existed and I say it existed (most likely) in the same form as we see it now, is some other manifold, i.e I do not agree with this idea of a singularity.

      Reply

  94. We notice a big misleading phenomenon in math. , when equations equate x and y to zero since they have -/+ signs it neglect that in reality , in physical realm , x and y really existed despite x+y =0 in equations , this allows for big confusion in grasping the physical reality itself , so when i say that ( i moved+ , earth moved -) , i + earth momentum =0 , this does NOT negate that the system components really and physically MOVED .

    Reply

    1. Think vector, NOT scalar. 🙂

      Prof Strassler, was Stephen Hawking correct in proclaiming that God is no longer required to explain “our” equations? (in reference to him accepting M-Theory as “valid”)

      Reply

      1. Hawking is of course entitled to his opinion, but I do not see how we can do an experimental test of his proclamation, or of any opposing viewpoint, to determine which is correct. For this reason I do not view his opinion as a scientific judgement, but as a statement of personal belief. And I am in no position to declare his personal belief “correct” or “incorrect”; it’s what he believes.

        However, this question deserves a much longer and much more carefully written answer, and I don’t want to try to do it haphazardly.

        Reply

      2. I’m confused about your answer, Prof Strassler.

        The proclamation was that X is no longer required to explain specific equations.

        Why is that not experimentally verifiable? If an observed phenomenon is explained using certain mathematical explanations, why are other explanations needed, no matter what you call them?

        Are you sure that you are not allowing yourself to be emotionally biased by the term “God” in the proclamation?

        Similarly, I see tremendous opposition to Victor Stenger’s rather simple proclamation that any interventionist God, even if it’s own actions are not constrained by natural laws as we understand them, would necessarily leave behind physical traces of its intervention, and that, given the utter absence of such traces, a god hypothesis is simply not necessary (as Laplace (probably apocryphally) said)?

        No more than frog burps are necessary to explain the Big Bang. It’s not a matter of “personal belief”, it follows from the math, doesn’t it?

        I’m not asking to provoke a theological or philosophical discussion at all; this is, as far as I can tell, purely a scientific, empirical and logical question – does process x require explanation z, or it is adequately and even completely explained via explanation y?

        The only hitch seems to be the emotional weight (as opposed to any actual mass-energy) of the term “God” as opposed to “magic” or “elves” or “Bigfoot”.

        Surely there are plenty of gaps for gods to hide – for example, as you noted, we don’t understand conscioussness – yet. But where in the Pythagorean equations you explain above is there a requirement for a supernatural factor?

        Reply

      3. David,

        I hope you are not suggesting we have all the questions, never mind the answers, that can be be asked? As long as we have unknowns and given the beautiful order and inherent logic of this magnificent universe, the explanation of intelligent design and universal consciousness (which ours could very well be entangled to) will remain a viable one.

        What Dr Hawking elected to reject is that we do not have all the physics to validate our math, yet.

        The physics we have thus far has been derived by the constraints we can deduce by this universe, in this cycle, with these initial conditions. What makes you and Dr Hawking so sure that the physics will be that same in the next cycle and/or the adjacent manifolds?

        The Big Bang is not the beginning, only a transition point of pulse we know nothing about, yet. God is still there.

        Reply

  95. >> “whenever there is a symmetry of the laws of nature.”

    Are the type of allowed the laws of nature restricted to allow Noether’s theorem to work. For example if we had a law with non-local action and also time-translation symmetry would that imply energy was only conserved globally but not locally ?

    Reply

    1. A good but very technical question; but it is really far beyond the scope of this pedagogical webpage. I have to think it over, but your best bet is to try it yourself and see whether the theorem’s conditions require locality. Today is a busy day and I will not have time to consider it.

      Reply

  96. That is fine , but it misses a fundamental fact, that a real movement of me and the earth really happened DUE TO NON-PHYSICAL causal something , you ignored the fact that the system ( me + earth) started with no movement , ended with real movement even in opposite directions with no causal physical measured something.
    As for mass , you skipped giving a definition of it ! well , you gave a circular one , mass = E /c^2 , but what is mass ? it is a property but what is its meaning ? what do we physically mean by saying electron mass is ……… kilograms ? ……..kilograms of what ?

    Reply

    1. No, my answer doesn’t miss any fundamental facts; I answered the question you asked.

      What you are asking now (in the first half of the current message) is this: where did the *energy* of your motion come from? We started with two things that have no motion-energy and only mass-energy (you and the earth), and then (without apparently changing their mass-energy) we ended up with both objects moving, and therefore some motion-energy. Where did it come from? Again, the classic freshman-year question.

      It came from your body. You used stored chemical energy and converted it into electrical impulses, which caused muscle contractions that allowed you to change the configuration of your body (in particular, to lift your leg and move it to the side.) This is why you need to eat; you need to obtain stored energy from outside sources so that you can use it later to move (including to breathe.)

      Fortunately, although you and the earth will have equal and opposite momentum when you start walking, the change in your motion-energy is far larger than that for the earth. That means that you only need to convert your stored chemical energy into your own motion-energy; you don’t have to waste it on the earth’s motion-energy. You would have to use more energy if you were walking on a skateboard, since you’d be giving the skateboard substantial motion-energy as well as yourself.

      Get yourself a big skateboard or a table with wheels and try it! It’s very entertaining, as well as illuminating.

      As for mass and its definition, yes, it needs more fleshing out. Patience.

      Reply

  97. Great article. Typo in the second paragraph of the “But Velocity is Relative” section?
    —
    If you’re sitting at home reading a book, you would claim the book has zero velocity (and relative to you, it does not)
    —

    Reply

  98. If i was sitting not moving then my momentum = zero , now by an act of conscious will i started to run , my momentum changed without any physical external action , here p is NOT conserved , am i wrong???

    Reply

    1. A classic! Your momentum changed, but so did that of the earth. You went forward, the earth went a very, very, very, very tiny bit backward. The total momentum of the system — you AND the earth — did not change at all.

      What, you didn’t notice the earth move?! 🙂

      This is every freshman’s confusion in week three of physics class. It’s a natural one; perfect Aristotelian thinking.

      Momentum involves velocity AND mass. An extremely massive object like the earth can change its momentum by a substantial amount without changing its velocity by something you can measure.

      Imagine that you were standing on a platform with wheels, like a skateboard, only bigger. Now start walking. You will go forward. The skateboard will go backward. The more massive the skateboard, the slower it will go backward. If you make it as big as a truck, you probably won’t notice it moving backward anymore, because of how slowly it moves. By the time you make it as big as the earth, you will not see any motion even with the most precise possible measurements.

      The fact that the earth is incredibly massive makes it possible to move however we like, barely disturbing the earth at all, while still conserving momentum. In general, an extremely massive object acts like a momentum-sink; it can absorb momentum without you being able to tell it has done so.

      Newton was a smart fellow to figure this out.

      Let’s be precise; imagine you start moving at one meter per second. How much will the earth’s velocity change? Let’s say you have a mass of 60 kilograms; the earth has a mass of about 6,000,000,000,000,000,000,000,000 kilograms (it is a 100 million billion [U.S. counting] times heavier); so when you start walking forward at 1 meter per second, the earth will move backward at .000,000,000,000,000,000,000,01 meters per second (100 million billion times slower). For comparison, the width of an atom is something like 0.000,000,000,1 meters; so at this rate it will take the earth 10,000,000,000,000 seconds, or about 300 thousand years, to move the length of one atom, and 3,000,000,000,000,000 years to move one meter. (That’s almost 300 times longer than the time since the Big Bang!)

      So that’s why you can’t tell that the earth moved backwards!!!

      Reply

      1. Longer than that, it’s actually 300 thousand times longer than the time since the Big Bang!.

        Reply

  99. “a massive Higgs particle (if such things exist, and they probably do) can decay into two massless photons”

    Errr… this is badly misleading. You are inviting people to think that the mass of a system is equal to the sum of the masses of its constituents, which of course is untrue. Each photon is massless, but the system consisting of two photons is not massless — it has the same mass as the higgs. Must be so, because mass is the length of the momentum four-vector, and four-momentum is conserved…..

    Reply

    1. If I stopped here, you are right, this would be badly misleading. But in the next installment, I’m going to explain this in detail, by studying this decay in several frames, and noting the difference between the sum of the masses of constituents and the “invariant mass” of constituents, which of course is not the same thing.

      The problem is that you’re thinking like an expert; it’s so easy for us to forget what it is like to be a layperson. You have to get unconfused in the right ways first before you can be taught what’s really going on. Most people are taught that mass is conserved in chemistry class. We have to unteach that first, then fix it properly; otherwise people end up terribly confused.

      As you say, the mass of a system is NOT the mass of its constituents, but the energy of the system divided by c^2. And the mass of a system is conserved, NOT because there is a third conservation law, but simply because energy is conserved.

      The logic is
      a) Energy and momentum are conserved;
      b) a mass of a system is not the sum of the masses of its constituents but the energies of its constituents and their relationships to each other (a very confusing notion at first);
      a+b) it follows logically from these two principles that the mass of a system is conserved, without the need for a law of conservation of mass, which would be false.

      So that is my pedagogical logic. I think you’ll like how this works out in the end.

      Reply

  100. “Pick any direction in space; then, according to Noether, momentum along that direction is conserved. And since there are three dimensions of space, with three independent directions you could go, there are three independent conservation laws.”

    Are the conservation laws sufficient to rule out other dimensions?

    Reply

    1. No; there may simply be conservation laws that we haven’t discovered yet. This is a long story though, You may want to read through my extra dimension articles.

      Reply

  101. I’ve never written a piece fan-mail before before and am not sure what to do. (Should I link to a picture of my underwear and pretend I’m throwing them at you?)
    Anyway, I’ve only been browsing your articles for a few weeks and I think I;m going to backtrack. They (and you) are articulate and accessible without being condescending and that is a true talent. This article in particular cleared up a mass-matter misconception that I didn’t know I had and made things a lot clearer.
    I (like Harry, but different) switched majors from theoretical physics to computer science but it was because it was in the mid-70’s before the standard model was, well, standard and string was in it’s infancy with 24 dimensions and most of the QM proofs had yet to come. GR I like to think I have a good grasp on but the higher math is beyond me.
    I’m currently going through the SM Tutorials for the masses to catch up on what I’ve missed, but end up following the links and their links so the going is slow, but steady, and endlessly interesting.

    I have a favour to ask of you. (hey, I’m recommending you to everyone on all the other blogs I haunt, so you owe me).:)

    Their is a contributor (troll) on one of the sites that I regularly visit who has his own TOE (which is fine) but insists on flogging it to everyone with a real question on physics (which is not). I’ve visited his site and the number of errors is astounding but when I point them out I get the ‘you are too stupid to understand’ argument which comes from the ’causeIsayso’ school of thought. (e.g. an angstrom is the width of an atom because the picture of a helium atom on wiki:atom had the angstrom length on the bottom as a scale).

    If you want a few minutes of fun I would appreciate you taking a look and giving your opinion. I know I have no right to ask but this guy is driving me and everyone else on the blog nuts. It is the blog of a famous TV personality theoretical physicist and I am especially disturbed when young people visit, post a legitimate question, he posts his ‘answer’ and they are never heard of again. (not moderated).

    I know you’re busy so reply if you want to and I’ll give you the link, otherwise I will not be offended. It won’t stop me from recommending you to everyone interested in intelligible physics articles. Great job!

    Reply
  102. Pingback: Standard Model Tutorials for the Masses (…er, sorry about the pun…) | Whiskey…Tango…Foxtrot?

  103. I agree, this is one of the best personal websites I’ve found on the ‘net. Thank you for doing this.

    The oversimplification in my undergrad physics classes (geared towards non-phsyics majors) was patently obvious once I did a little reading of my own on particle physics and relativity. Your website has been immeasurably helpful in clearing up some misconceptions I’ve had and gives a good overview of current developements in physics.

    Reply

  104. Thank you, Prof. Strassler. Another excellent article that makes complex concepts accessible to laymen like me.

    I hope you appreciate, not only how enjoyable and informative these articles, but how essential they are to the health and sustainability of our society.

    Widespread ignorance of and misunderstanding with regard to the nature of scientific inquiry and the discoveries and insights of modern science endanger us all.

    When public policy is made by scientifically illiterate elected officials in response to public pressure from scientifically illiterate voters, we all suffer the consequences.

    When scientific illiteracy fuels outright hostility to science and reason, those consequences can be catastrophic.

    We’re not just fighting Young Earth creationists these days; a lot of pernicious New Age quantum flapdoodle depends upon public ignorance of precisely the things you talk about on this site.

    Thanks again. I hope more of your colleagues follow your example.

    Reply

  105. You have described energy as the work that massive particles can do, however, what is energy in it’s fundamental form where there is no mass.

    Yes, Planck by studying the effects of energy through various instruments and sensors converged to the now famous equation E = hv , but that is just the effects.

    What is the cause, E?

    Where did it, E, come from?

    Is it really a conserved quantity or is it our limitation, our inability to remove ourselves from our own universe (outside reference frame) that leads us to believe it is a constant?

    Why was entropy what it was at the initial conditions, Big Bang, or our universe?

    Is there a contradiction in our physics, flawed math? The math we have “invented” would leads us to a universe of an equilibrium state, maximum entropy, and yet the same math is used to describe the Big Bang. I see the two phases of our universe, the Big Bang and maximum entropy, as contradictory. In other words, our math tells us of a beginning and an end. That is the biggest contradiction in our conscious existence.

    What is E?

    Reply

    1. I told you in the article; it is the conserved quantity that, in any physical system with time-independent equations, can be written down using Noether’s theorem. Give me a physical system with equations that describe it; I will write down for you what E is.

      Typically it is easier than this. I can write down E using earlier equations, called the Euler-Lagrange equations. There are other approaches too.

      E is not some vague, ambiguous thing; we know exactly what it is.

      Also — energy is not “the work that massive particles can do”; you’re misinterpreting what I wrote.

      Reply

      1. Again, I apologize for my vague language. Let me try again to understand E.

        When I see an equation of the form E = some function of time-independent terms, I interpret that to be the description of the effects of energy in that particular system. What I am asking for is the cause of all this motion and matter we see in our universe.

        Let me try to steer you to the fundamental aspect of energy. The vacuum energy is the zero point energy of all the fields in space. Even the Higgs field, one of the most fundamental field in our universe has a fairly large VEV of 246 GeV. So would you agree that there is no point in space with a zero VEV. Now if one would to reverse the direction of time and go backwards toward the singularity, the fields start vanishing, the amplitudes of the vacuum fluctuations start decreasing until you are left with the maximum energy (not infinite, but maximum) with zero dimensions at t = some very infinitesimal quantity, (but not zero and certainly not negative). How would you describe energy in that phase and can we deduce a numerical number of the highest possible density (energy) that existed at that point (non-zero) from the visible universe?

        This layman’s question is, Prof Strassler, could all this energy that we see and measure exist in such an infinitesimal spacetime point like the mathematical formulation of the singularity or was the Big Bang a rupture from another manifold pouring this energy and creating our manifold. The particular flux of this energy pouring in could explain the initial entropy which our universe started with and also why matter won over antimatter. But even in this scenario I can understand and visualize the effects of energy but I still cannot get my mind around what it is, the cause.

        Reply

  106. Good old fashioned cliff-hanger, eh Matt? I’ve been looking forward to a post like this for a long time; looking forward to the next one. Been wondering how intimate we are with understanding and manipulating this relationship between mass and energy.

    I think nuclear power takes advantage of this (E=mc^2), right? But anything else? LHC does too, right? Are there any other applications where this mass-energy relationship has moved beyond theory? Like in computing or power generation? You know, Star Trek replicator kind of thing — which sounds more like it falls into the fallacious “matter” – energy assumption.

    What do you think would be the ultimate expression of our understanding of the mass-energy relationship? What would be a life-changing example that demonstrates how well we could manipulate what we know into a technological advancement?

    By the way, I have a little cartoon about the Higg’s boson and black holes:
    http://wp.me/p1SONx-7T

    There’ll be another about the superluminal neutrinos in a week or so. Something about those tiny particles smashing together that just gets my imagination running…hope you enjoy the bit of humor.

    I look forward to your following posts.

    Tim
    scienceforfiction.com

    Reply

    1. I only write cliff-hangers; there’s so much to learn that there is always another chapter.

      The relation between mass, energy and momentum that Einstein figured out is extremely well understood. Every aspect of nuclear physics and particle physics relies upon it. Everything done at the Large Hadron Collider depends upon it — what we know about the proton’s structure from previous experiments; how you accelerate, steer and collide the protons; how you measure the debris from the collisions; how you infer what may have happened in a collision from those measurements; how you predict the rates for certain expected processes and recognize new ones. This is true of all particle accelerators since the very first ones. Almost every discovery in particle physics in the last eight decades has used these relations. Much of what we know in astronomy and cosmology uses them.

      This relation is crucial in those aspects of nuclear physics that affect us most; why some atomic nuclei beyond hydrogen can be stable even though neutrons on their own are not; why the sun’s furnace works; how the earth stays warm and geologically active; the risks and rewards of radioactivity (i.e. the decay of a nucleus or other particle.)

      The most direct way that we might come across this outside of nuclear physics is in PET scans. There, a tiny amount of material that emits positrons is put into our bodies and absorbed, say, by a tumor, and the emitted positron annihilates with an electron (see my particle-antiparticle annihilation article) to make two photons that we can detect, showing us where the tumor is.

      I’m sure there are other examples I just can’t think of.

      Reply

      1. Hello Matt,
        Thank you for taking the time to write this piece. It has helped me greatly.
        I would like to ask your opinion on a couple of definitions I have pondered on in an attempt to understand this subject from a background in electronics:
        1. Could ENERGY be adequately defined as ‘the capacity to induce change” [in some parameter] and
        2. Could a photon be defined as a carrier of “evidence” of such a change ?
        Just to clarify (1):
        Wherever there is energy, there is change (in velocity, temperature, momentum, brightness or voltage etc)
        Conversely, wherever there is change, there is energy. Also, where there is no energy there is no change and where there is no change, there is no energy.
        To clarify (2)
        Is it not true that every photon has it’s source in something (or some system) that exhibited a change of energy state (eg electron changing orbit, a decaying particle, collision etc) ?

        Reply

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Search

Recent Posts

Buy The Book

Reading My Book?

Got a question? Ask it here.

Media Inquiries

For media inquiries, click here.

Order Waves In An Impossible Sea

Harvard Book Store
Amazon
Audiobook: Audible
Barnes & Noble
Powell's Books
Elliot Bay Book Company
Vroman's Bookstore