Matt Strassler [January 14, 2013]
What keeps the electrons in an atom trapped around the nucleus of the atom?
Well, at first glance (especially when we look at the cartoon version of an atom, whose limitations I described) the electrons orbiting the nucleus of an atom look naively like the planets orbiting the sun. And naively, there’s a similar effect at work. Only it will turn out there’s a twist.
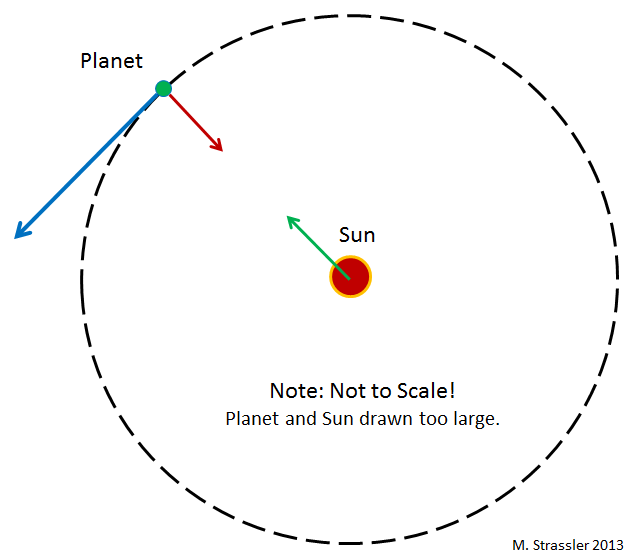
What keeps the planets orbiting the sun? In Newton’s view of gravity (Einstein’s is a bit more complicated, but we don’t need it here) any pair of objects pull on each other via gravitational forces proportional to the products of the two objects’ masses. In particular, the sun’s gravity pulls the planets toward the sun (with a force that is inversely proportional to the square of the distance between them… in other words, if you make the distance half as big, the force gets stronger by a factor of four.) The planets each pull on the sun, too, but the sun is so heavy that the pull has almost no effect on how the sun moves.
The tendency (called “inertia”) of all objects to travel in straight lines, when unaffected by other things, works against this gravitational pull, in such a way that the planets travel in orbits around the sun. This is shown in Figure 1, for a circular orbit. In general these orbits are ellipses — though these orbits are nearly circular for the planets, as a result of how they formed. (Not so for various smaller rocks [asteroids] and iceballs [comets] that orbit the sun.)
In a similar way, all pairs of electrically charged objects pull or push on each other, again with a force that varies with the inverse of the square of the distance between the objects. Unlike gravity, however, which (for Newton) always pulls objects together, electrical forces can push or pull. Objects which both have positive electric charge push each other away, as do those which both have negative electric charge. Meanwhile a negatively charged object will pull a positively charged object toward it, and vice versa. Hence the romantic phrase: “opposites attract”.
So the positively-charged atomic nucleus at the center of an atom pulls the lightweight electrons at the outskirts of an atom toward it, much as the sun pulls on the planets. (And similarly the electrons pull on the nucleus, but the mass of the nucleus is so much larger than that of the electrons that the pull has almost no effect on the nucleus. The electrons also push on each other, which is part [but only part] of the reason they don’t tend to spend too much time very close to each other.) Naively, then, the electrons in an atom could travel on orbits around the nucleus in much the same way as the planets travel around the sun. And naively, at first glance, that’s what they seem to do, especially in the cartoon atom.
But here’s the twist — actually it is a double-twist, each twist creating an opposite effect, so that they cancel each other out!
The Double Twist: How Atoms Differ From Planet-Sun Systems
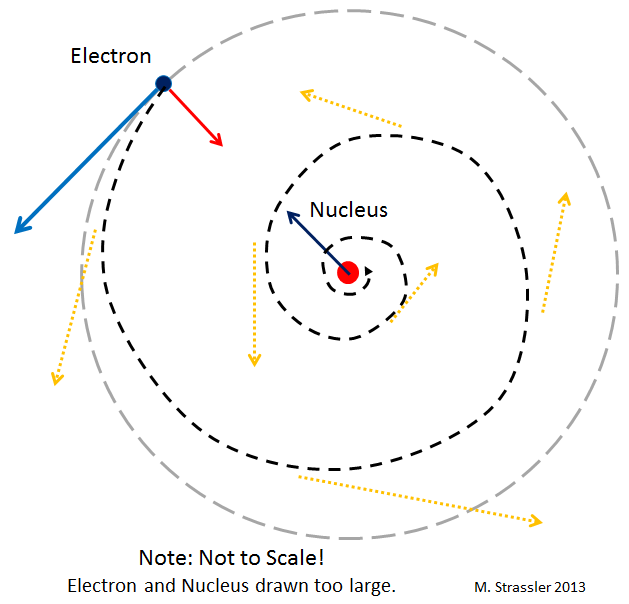
First twist: Unlike planets around the sun, electrons orbiting the nucleus should — naively — be able to radiate light (or more generally, electromagnetic waves, of which visible light is just an example). And this radiation— naively — should cause the electrons to slow down and spiral into the nucleus! (There is actually a similar effect in Einstein’s theory of gravity; the planets can radiate gravitational waves. But the effect is incredibly tiny. Not so for electrons.) Naively an atom’s electrons should spiral into the nucleus in a tiny fraction of a second!
And if it weren’t for quantum mechanics, they would! This potential disaster is illustrated in Figure 2.
Second twist: But our world operates according to principles of quantum mechanics! And quantum mechanics comes armed with an amazing counter-intuitive principle, the uncertainty principle. This principle, which reflects the fact that electrons are as much waves as particles, is something that deserves a long article of its own; but for today, here’s what we need to know about it. The general consequence of the uncertainty principle is that not all aspects of an object can be simultaneously known; there are certain aspects for which measuring one precisely makes the other uncertain, and vice versa. A specific case involves the position and velocity of “particles” like electrons; if you know exactly where an electron is, you don’t know where it’s going, and vice versa. You can compromise, and know to some extent where it is and to some extent where it is going. In fact, that’s the situation in an atom. Let’s see why.
Suppose an electron spiraled down toward the nucleus as in Figure 2. Well as it did so, we would know better and better where it was located. The uncertainty principle would then tell us that its velocity would have to become more and more uncertain. But if the electron came to a stop at the location of the nucleus, its velocity would not be uncertain! So it can’t stop. Instead, as it tried to spiral in, it would have to move with a faster and faster random motion. And this increased motion would in turn fling the electron away from the nucleus!
The tendency to spiral inward is thus counteracted by the tendency to move more quickly due to the uncertainty principle. A balance is found when the electron reaches a preferred distance from the nucleus, and that distance that sets the size of atoms!

If the electron is initially very far from the atomic nucleus, it will initially spiral, as shown in Figure 2, by radiating electromagnetic waves. But eventually its distance from the nucleus is small enough that, as described in the preceding paragraph, the uncertainty principle prevents any further approach. At that stage, where the balance between radiation and uncertainty is found, the electron establishes a stable “orbit” around the nucleus (or better, an “orbital”, a name which is chosen to reflect the fact that, unlike a planet, an electron spreads out in a very non-particle-like way, thanks to quantum mechanics, and doesn’t really have an orbit like a planet does). The radius of that orbital sets the radius of an atom. See Figure 3.
There’s another feature — the fact that electrons are fermions — that causes the electrons not all to go down to the same radius, instead they stack up into “orbitals” of different radius. I won’t go into this here, but it will come up again in another article.
How Big are Atoms? An Estimate from the Uncertainty Principle
In fact (for readers who are so inclined — there’s a little bit of algebra involved) we can estimate the size of an atom by using only the force law for electrical forces, the mass of the electron, and the uncertainty principle! You can skip this part if you want, but it’s so much fun: watch how easy it is to deduce the basic size of atoms! To keep this simple, let’s do this for hydrogen, where the nucleus consists of just one proton, and there’s just one electron around it.
- Let’s call the electron’s mass me.
- Let’s call the uncertainty in an electron’s position Δx
- Let’s call the uncertainty in an electrons velocity Δv
The uncertainty principle says
- me (Δ v) (Δ x) ≥ ℏ
where ℏ is Planck’s constant h divided by 2 π. Notice this says that (Δ v) (Δ x) can’t be too small, which means the two uncertainties can’t both be really small — that’s the point! — though you could have one uncertainty be really small as long as the other uncertainty was really big.
When an atom settles down to its preferred “ground state”, we can expect that the “≥” sign turns into a “~” sign, where A ~ B means “A and B aren’t quite equal, but they aren’t very different either.” This is a very useful symbol when making estimates!
In short, for a hydrogen atom in its ground state, for which the uncertainty in position Δx will be of order the radius of the atom R, and the uncertainty in velocity Δv will be of order the typical speed V of the electron as it orbits the atom, we have
- me V R ~ ℏ
Now how do we figure out V and R? There’s a relationship between them and the force that holds an atom together. In non-quantum physics, an object of mass m in circular orbit of radius r and moving with speed v around a central object which pulls on it with mass F satisfies
- F = mv2/r
This won’t apply exactly to an electron in an atom, but it will do so approximately. The force acting on the atom is an electric force exerted by the proton (of charge +1) on the electron (of charge -1), and that takes the form
- F = ke2/r2 = α ℏ c / r2
where k is Columb’s constant, e is the fundamental unit of electric charge, c is the speed of light, again ℏ is Planck’s constant h divided by 2π, and we have defined the “fine-structure constant” α = ke2/ℏc ~ 1/137.04… or so. Putting the previous two equations for F together as an approximate relationship gives
- α ℏ c / r2 ~ mv2/r
Now let’s apply that for our atom, letting v → V, r → R, and m → me. And let’s also multiply the above equation by me R³. This gives
- α ℏ c me R ~ me2 V2 R2 = (me V R)2 ~ ℏ2
where in the last step we used the uncertainty relationship for our atom, me V R ~ ℏ. Now we can solve for the radius of the atom R, finding
R ~ ℏ / (α c me) ~ 137 (10-34 kg m²/s) / (3·108 m/s · 9·10-31 kg) ~ 0.5 · 10-10 m
which is just about right! Simple-minded estimates like this won’t get you precise answers, but they will give you accurate answers!


59 Responses
I’m a scientist and I personally think this is a really great example
Why would it violate the uncertainty principle for an electron to be precisely at the nucleus, but it doesn’t violate the uncertainty principle for a proton or neutron to be precisely at the nucleus?
JohnChrysostom, the protons and neutrons aren’t precisely at the nucleus either. They are also “smeared out”, but due to their much higher masses, in a lot smaller volume, so to speak. Note how the uncertainty principle includes mass – all else equal, a proton with the same “uncertainty” of position will have roughly 1800 times less “uncertainty” of momentum than an electron, which means the nucleus is a lot more compact than the atom. But that’s electromagnetism, and electromagnetism has positive binding energy in the nucleus, not negative. To get the size of the nucleus, you need to deal with the strong force, which is a lot trickier. The naïve approach still works fairly well for hydrogen – with coupling constant equal to one (true enough at this distance) and mass 1800 times electron’s, you get that the nucleus is roughly five orders of magnitude smaller than the atom, pretty close to reality. Mind you, I’m no physicist, so take all this with huge grains of salt – I might be making some elementary mistakes. But the basic idea should be right – higher mass and stronger attraction means smaller “uncertainty”. Analogously to electron orbitals and shells, protons and neutrons in the nucleus also have their nuclear orbitals and shells. These are very important for nuclear physics, but don’t really matter much to chemistry – from the point of view of the valence electrons, the nucleus might as well be a point charge.
Many thanks. That was a succinct summary of some issues that had puzzled me. (It also raises the question of whether EC decay can be affected by the chemical environment of an atom since in the case of s orbitals at least this should affect the probability of finding an electron close to the nucleus.) Again, many thanks for taking your time to answer these queries.
Almost missed this article, another excellent read with an elegant (if approximate) example. Some questions:
The proton and electron orbit their baryocenter, I am looking through some of the models on this page but do not quite understand them enough to answer this; would tauonic hydrogen have the proton and tau spread over approximately the same area of space (1777 MeV\c vs 938 MeV\c masses respectively) and would this affect the shape of the resulting orbital?
An electron cannot spiral into a proton and annihilate, yet an electron and positron can, despite being able to form a (meta)stable state, positronium. Why is this? Is it in fact ‘stable’ but in that state the electron and positron can occupy the same volume of space and thus ‘meet’ and annihilate? (Whereas the proton and electron would require an antineutrino as well I believe.) Or is it that the hydrogen atom is the lowest energy state (A neutron being heavier than a proton plus an electron.) In *that* case, if I had a nucleus that was unstable with ‘too many’ protons, could an electron spiral into it emitting radiation, or would another process take over?
Tauonic hydrogen wouldn’t be that different from positronium, in which the electron and anti-electron (i.e. “positron”) have the same mass. The orbitals don’t depend on the relative masses; they would have exactly the same shape for any two pointlike particles, independent of their masses. But the orbital describes the probability for the distance between the two particles to be a certain size, and how that translates into the motions of the two particles depends on their relative mass.
Even in the case of tauonic hydrogen, the atom would be 60 times bigger than the proton, so the proton’s size would still be a small correction to this statement.
——-
“An electron cannot spiral into a proton and annihilate, yet an electron and positron can, despite being able to form a (meta)stable state, positronium.”
The electron and the positron DO NOT spiral in, first of all, and they do not radiate before they annihilate. It is simply that they have a certain probability of being close enough together to annihilate. In positronium, although the average distance between the electron and the positron is about .25 x 10^-10 meters, there is a non-zero though small probability that they will be much closer than this. (The orbital does not vanish at zero electron-positron separation.) When they are sufficiently close together the probability for the process electron + positron –> photon + photon becomes large enough that it may occur.
For the same reason, there is a certain very small probability (without any spiraling and without any radiation) that the electron is to be found inside the proton. The reason the process proton + electron –> neutron + neutrino does not occur is that it is forbidden by energy conservation: m_proton + m_electron [where m_X means “the mass of X”] is less than m_neutron + m_neutrino, so this transition would require an outside source of energy.
Even if the process were allowed, it would be very slow, because it proceeds via the weak nuclear interaction (specifically via a virtual W), which has a range of 10^(-18) meters due to the heavy mass of the W particle. And indeed, for some radioactive nuclei, “electron capture”, in which electron + proton –> neutron + neutrino inside a nucleus, is allowed, because the binding energy of the nuclei involved make this energetically possible. I don’t know how good or accurate the wikipedia article is but it will get you started: http://en.wikipedia.org/wiki/Electron_capture
Dear Michael Chisnall, your reasoning about quantization of the nucleus orbital momentum is wrong – as a matter of fact, both electron and the nucleus are in a mixed state in an atom. Although the nucleus does not stay in the barycenter, its “positive charge formfactor” can only be probed by an external particle (projectile), not with the atomic electron. You can find about orbital momenta here http://vladimirkalitvianski.wordpress.com/2011/01/04/unknown-physics-of-particle-orbital-momentum-in-qm/
and about the atomic positive charge form-factor here http://vladimirkalitvianski.wordpress.com/2010/12/02/zoom-in-atom-or-unknown-physics-of-short-distances/
Everything is substantiated quantitatively.
Why do people always assume that the nucleus is at the geometric center of the hydrogen atom? Urey famously pointed out the nucleus and the electron would orbit their barycenter. People usually take his observation and then use a nucleocentric model with an electron with a ‘reduced mass’ to calculate energy levels. But surely Urey was right. In a bohr like model the electron and the proton would orbit the barycenter and they would BOTH have orbital angular momentum, which would be quantised. When the electron is in its n=1 orbit then the proton would be in its n=1 nuclear orbit. If the electron jumps to an n=2 orbit then the proton might likewise jump to its n=2 nuclear orbit, and so on. This leads to revised Bohr like model with some differences from the classical Bohr model.
I do recall reading somewhere that there was some sort of problem in nuclear chemistry in predicting the nuclear spins of different elements. If I’m remembering correctly – not guaranteed – the spins of the individual nucleons don’t always add up to give the observed nuclear spins. I’ve often wondered whether this was because they were using a nucleocentric model and whether this problem would disappear if some nuclei turned out to have orbital angular momentum, as well an intrinsic spin, which needed to be taken into account.
There would be other consequences. If the nucleus sometimes has orbital angular momentum then its wavefunction would be smeared out over its orbit, rather than just the center of the atom. This would presumably impact on the calculations involved in measuring its size. Since the size of the nuclear orbit would be different if the electron was replaced with a muon, a failure to take this into account might explain recently reported discrepencies in the measurement of the size of the proton.
Nuclear orbital angular momentum would add an extra source of symmetry that needed to be taken into account in the beta-decay of cobalt-60.
The magnetic moment of the nucleus would not just include the intrinsic spin but would now include a component from the orbital momentum. In principal this means that the magnetic moment of a hydrogen nucleus would differ slightly from a free proton but the difference is only about 1 part in 10^4. Excited nuclei – like the metastable helium found in lasers everywhere – would sometimes have different magnetic moments from their ground states which seems like something that might have been noticed.
(I do recall once starting to look at what a fully quantum-mechanical version of this model would look like, with Schrodinger’s equation, but it turns out the differences are big compared to the standard account and I never really finished it).
“People usually take his observation and then use a nucleocentric model with an electron with a ‘reduced mass’ to calculate energy levels. ”
That’s not correct. That’s not what they do. They use a barycentric model with a reduced mass. You’ve misinterpreted it as a nucleocentric model, but if you go through the math properly, it is a barycentric model. And you can prove that there is only ONE l-quantum number — not two — in the theory. It’s all very rigorous mathematics; for a single electron around a nucleus, there are no approximations made in the calculation, and your statement about there being two orbital quantum numbers is simply not correct. The mistake you are making is assuming that the orbital angular momentum quantum number gives the angular momentum of the electron. This is incorrect. It gives the angular momentum of the electron and nucleus SYSTEM as they orbit their barycenter. It is the angular momentum of the SYSTEM that is quantized.
“If the nucleus sometimes has orbital angular momentum then its wavefunction would be smeared out over its orbit, rather than just the center of the atom.”
This statement misses the point. Even in the standard calculation that you criticize, the nucleus’s wave function IS smeared out over its orbit (because the electron and nucleus orbit their barycenter.) [When you write the wave function Psi(R,r), where R is the three-dimensional location of the barycenter and r is the distance between the electron and the nucleus, the nucleus is not located at R.] And this effect is most certainly accounted for in measurements of the proton’s and nucleus’s size.
So I would suggest that you go back and study the original calculation in quantum mechanics textbooks, and verify what I have told you by going through the math properly. Otherwise you’ll be wasting even more of your time, I fear.
Are we talking at cross purposes here? My claim is most certainly correct. You do not use a reduced mass with the barycentric model. There are three possible models here: (i) the classical nucleocentric Bohr model, (ii) the barycentric Bohr model, (iii) The nucleocentric model with a reduced electron mass. The last two models are mathematically equivalent. As the Wikipedia points out, the reduced mass is “a quantity which allows the two-body problem to be solved as if it were a one-body problem”, i.e. you take a barycentric model then transform it mathematically into a nucleocentric model with reduced masses. Essentially you are rebracketing terms.
Sorry if I wasn’t making it clear but I wasn’t implying that there were two quantum numbers involved. In a barycentric model the total angular momentum is quantized and I wasn’t implying otherwise. However both particles will have orbital angular momentum. In the lowest energy state, the electron and proton will orbit at a particular distance from the barycenter, and at higher energy states the electron and proton will each orbit at different distances from the barycenter. In the nucleocentric Bohr model you end up with distinct orbits for the different energy states and the same thing will be true in the barycentric model, except that it won’t just be the electron that has distinct orbits – the proton will also have distinct orbits – each one corresponding to an different electron orbit. Hopefully this is clearer as to what I meant.
One of the consequences, as I mentioned in my previous comment is that there should be an impact on the nuclear moment of the hydrogen nucleus. All the accounts I’ve seen for calculating the magnetic moment use the intrinsic spin and a lande factor, but make no room for a component from orbital motion of the nucleus. Even looking at papers on Arxiv on measuring the proton’s moment I don’t see any mention of this (e.g. this from 2011).
You suggested I should study the calculations in QM textbooks, do you have suggestions for which ones? This isn’t covered in Rohlf’s book, although that is admittedly a low-level book. I’ve never seen this discussed in any QM book I’ve look at – Kalitvianski’s webpage, below, is the first account I’ve seen. Nuclear motion is mentioned in passing when discussing the Born-Oppenheimer approximation but that concerns molecules. I’ve never seen a book which discuss nuclear motion in the context of an unbound hydrogen atom.
No matter how you do the calculation, the atom consisting of an electron and a proton has 2×3 = 6 positions that describe it. Three (X,Y,Z) are used to give the center-of-mass position of the atom. The other three (x,y,z) give the distance between the electron and proton. Now: the statement
“it won’t just be the electron that has distinct orbits – the proton will also have distinct orbits – each one corresponding to an different electron orbit. ”
is wrong. The electron-proton SYSTEM has distinct orbits, with a shape in the coordinates (x,y,z). You cannot say “the electron has an orbit and the proton has a corresponding orbit.” If that were true, you could imagine breaking the correspondence. But you cannot. If you assign the orbits to the electron and separately to the proton, as though they can be treated separately, you have misunderstood what the quantum mechanics equations are telling you. The effect that you call “the orbital motion of the nucleus” is already accounted for in the calculations — as is obvious to any good student, or expert — and that is why you never see anyone discuss it.
As I said before — the calculation of orbital motions of an electron around a nucleus is COMPLETE — no approximations are made. There is no room to insert anything else.
I’d like to thank Gaston E Nusimovich for his comment. I certainly couldn’t have said it as well!
The diagram of the electron orbiting the nucleus, with the analogy being made to a planet orbiting a star, suggests that the orbit should be planar. But the electron “orbitals” are three-dimensional.
That is correct. It is a limitation of the drawing and the text. Maybe I should clarify that the electron cloud is three-dimensional.
Sorry, my objection wasn’t worded clearly 🙂 In the article you use the case of gravity causing the planet to orbit a star, as an example to help understand electromagnetism causing the electron to orbit a nucleus (with the similarity being that both systems are governed by an inverse-square attractive force).
The laws of physics give us the fact that the planet moves in a planar orbit. But why does the electron not move in a planar orbit?
Because the electron is more wave than particle, and it wants to spread out around the atom. Trying to confine the electron to a plane raises the energy of the system; the lowest-energy state of the system will allow the electron to spread out more fully.
I also wanted to know why this is so.
Thank you, Old Wolf, for your excellent question.
and Thank you, Matt Strassler, for your excellent explanation.
🙂
To Dr. Matt Strassler,
Does “the angular momentum of an electron(=spin)” also want to spread out? If so, what “shape” does “the spread” have? (sphere/doughnut or something else? instead of a plane?) What does observation or theory say about its shape?
To Matt Strassler, you said “Because the electron is more wave than particle, and it wants to spread out around the atom.” What about the planets? Why are they not spread out around the sun like an electron around the atomic nucleus? because they are much more massive or because they are much larger than atom? or both. If so, why more massive or larger objects tend to exhibit less wave-like characteristics (do not want to spread out) and tend to stay on a plane? Does Higgs field play a role in the spread? if so how? Why staying in a plane in the planetary case has the lowest energy? Even a massive planet is spread out a tiny bit? If so, what is the approximate shape of the spread? Is it an elongated sphere along its traveling orbit? or something else?
Elm, if you only consider the gravitational attraction between the planet and the star, the planet would also prefer to be spread out (even better, it would love to be at the centre of the other mass!). However, that’s not enough – you also need a way to get rid of the extra energy and angular momentum. And that’s where the differences between planets and electrons really jumps out at you. First, gravity is absurdly weak as a force, and it would take far longer than the current age of the universe for it to radiate away enough energy to do that even if you ignore the attraction between the individual particles making up the planet (both gravitational and electromagnetic).
Not ignoring that gives another important point – electrons are not composite particles, unlike planets. The individual particles making up a planet attract each other, and have negative binding energy – spreading the planet on its orbit (“surface of an ellipsoid” in the simple case) would lower the binding energy of the Earth-Sun system, but not the Earth-itself system. That’s why planets formed from the cloud of debris in the first place – a ball of material has less energy than a dispersed cloud of material. Even with atoms with more than one electrons, there’s a crucial difference – pushing electrons closer together requires energy (the electromagnetic interaction between them is repulsive, the binding energy is positive), while pushing two rocks together releases energy (the gravitational interaction between them is attractive, the binding energy is negative). So electrons *really* want to be as far from one another as possible (minimising their positive binding energies), while still keeping as close to the nucleus as possible (minimising their negative binding energy). Gravity seems to always attract, so bigger density is always better if you only consider gravity – the reason the Earth isn’t denser is that the repulsive electromagnetic interaction prevents that – the result is a balance between the positive electromagnetic binding energies and the negative gravitational binding energies of the individual molecules.
Can the planet spiral *into* the Sun, then, and make a slightly bigger Sun-ball? Yes, but that requires it to get rid of the extra energy – and gravitational radiation isn’t enough for that. In the Earth-Sun system, the power radiated away through gravitational waves is just ~200 W – compare this to Earth’s kinetic energy (with respect to the Sun) of ~2.7E33. Ignoring all other effects and assuming the loss is constant (it isn’t, but it’s not all that important at age-of-universe-scales) would need about 4E23 years of gravitational radiation to get rid of that energy. There are examples of super-massive systems that do just that (still over large time scales) – two black holes closely orbiting each other and eventually merging together being probably the most obvious example (as LIGO has shown, the energy radiated away by gravity a few seconds before the merger is absurd, but it takes very short oscillations and large masses). That’s not going to happen for a typical planet orbiting its star.
In contrast, the electromagnetic force is strong enough that the electron usually radiates the extra energy in a fraction of a second – so you mostly see atoms in ground states or just a bit excited (e.g. when a photon is absorbed by the electron bumping it slightly “higher” in the potential well but before the electron emits another photon (or more) as it “drops” again).
Hi Matt. When describing the uncertainty principle , “not all aspects of an object can be simultaneously known”, you are picking a particular “interpretation of QM”. It seems more popular at the moment (some would say, more correct) to say that the object does not have such properties, and the property only exists when it is measured, and the “uncertainty principle” constrains the results of successive measurements of different properties.
I wonder if it is possible to re-word your article to avoid this topic (which I’m sure a lot more could be written about!) I would be very interested to read an explanation that doesn’t use the uncertainty principle causally, as you mention in another comment.
Secondly: you describe the electron as orbiting the nucleus. How accurate is it to say that? Can we actually say more than just that looking for an electron at a particular location has a particular probability of success. Most write-ups on atoms are rather unclear on this point.
I don’t know that there is an ideal way to deal with this challenge…
There’s a very precise set of mathematical equations for computing the wave function of an electron around a nucleus. The square of the wave function predicts the probability of finding the electron at any given point, should you choose to look for it.
However, what that all means for the reality of what an electron is, what it is doing, whether it is meaningful even to ask these questions, etc., is unclear. There isn’t a consensus on the best way to think about it. And that’s why all the write-ups are unclear.
Quantum mechanics works to tell you the outcome of experiments — probabilistically. It does not help you gain a picture of reality that is simultaneously complete, consistent and clear. You can have clear but not complete; you can have complete but not clear; you can have complete and clear but inconsistent. That’s where our understanding currently lies.
You use formula F = mv^2/r, BUT what is the true validity of that argument, even as an approximation? I see no point why that should hold to any degree on hydrogen atom. Uncertainity principle does not say anything like that, and it’s pure lucky to get correct answer. What is the REAL counter-force that creates that equilibrium state with Coulomb force?
Sure one can use Uncertainity principle e.g. for ground state of harmonic oscillator, but for hydrogen atom… I won’t belive it without some serious arguments and math.
U.P. and all other principles have no physical explanations , principles are fundamentals that cannot be explained by any more basic facts.
Just a minor point. If electrons are modelled as point particles then classically they should radiate in the nucleus. But the really interesting thing is that some accelerating continuous charge distributions don’t radiate!
The nonradiation condition has a long history:
http://en.wikipedia.org/wiki/Nonradiation_condition
Goedecke, G. H. (1964). “Classically Radiationless Motions and Possible Implications for Quantum Theory”. Physical Review 135: B281–B288. doi:10.1103/PhysRev.135.B281
RE. my first previous question :
But this is circular reasoning..U.P.depends on properties / properties depend on U.P. …
I can still ask :
what tell the electron that its position is entering a zone of certainty ? and what tell the electron : now you have to increase your speed…..
I am looking for the causal physical order / force / whatever that accomplish this.
The proper reasoning would be that the U.P. depends on some properties, and other properties depend on the U.P.
The uncertainty principle is a direct result (very roughly speaking) of the fundamental units of matter being waves and not point particles. This makes some intuitive sense; waves do not have an exact position in space, they are spread out. (The uncertainty in velocity is harder to visualize.) The final result is the same though, the U.P. isn’t affecting anything, it isn’t ‘forcing’ particles to behave in certain ways, those particles behave as they do because of what they *are*; it is the underlying principles that are doing the affecting.
You can think of it this way; air has no solid surface, no boundary because it is a gas. It expands into any available (lower pressure) space and a given volume will change in exact, mathematical ways as pressure or temperature change. Indeed there are a number of physical laws relating to these phenomena. But it is not the laws themselves that make air behave as it does, they are merely the result of what air IS, of some of its properties. It is those properties (Being small particles with very little attraction between them for instance) that govern its behavior and other properties (such as its density at room temperature and pressure.)
On my Android phone’s browser, the system fonts don’t include the Unicode hbar symbolℏ (U+210F), which makes the math pretty hard to follow! I suggest using an italicized ħ (U+0127) instead.
(Recommendation comes from .)
Sorry, that should say from http://stackoverflow.com/questions/5310346/missing-font-character-like-reduced-planck-constant .
Hello, thank you for this explanation. One question : is there a specific frequency to the electromagnetic waves emitted by the electrons accelerating and changing directions in the cloud ? Is it measurable and associated with a known physical principle ?
Thanks for the question — it points out a pedagogical problem with my explanation.
Once the atom settles into its ground state, the electrons don’t radiate anymore — they can’t. The system is in the lowest possible energy state and there’s no way for any more light to be emitted. I should have said this explicitly.
If you start with an electron that is much further from the nucleus than it would be in the ground state, then the electron *will* radiate light as it approaches the nucleus and the atom goes toward its ground state. And yes, because quantum mechanics only allows the electron to do certain things and not others, only certain frequencies of light will be emitted; these can be precisely calculated and measured. The allowed frequencies correspond to specific colors of light, and when passed through a prism are called “spectral lines”: here’s a photo showing some spectral lines associated with particular elements http://www.google.com/imgres?imgurl=http://scienceblogs.com/startswithabang/files/2012/10/atomic_line_spectra.png&imgrefurl=http://scienceblogs.com/startswithabang/2012/10/24/what-is-the-sun-made-out-of/&h=562&w=1015&sz=220&tbnid=wb6AGkTAr_6rmM:&tbnh=68&tbnw=122&zoom=1&usg=__ksEBTPgMOkzFsxvcLKOcTxWpmYA=&docid=5vbENk0exM2qEM&sa=X&ei=mrv2UNnFDrDJ0AHbh4CYDg&ved=0CGMQ9QEwBQ&dur=463
Ok thanks, that makes it clear. My confusion came from the fact that you mention “At that stage, where the balance between radiation and uncertainty is found, the electron establishes a stable “orbit”” in your article, which lead me to think that there was radiation emitted from the cloud.
Thanks again for your continuous effort to help us understand those principles.
Dear Matt,
I would like to point out two things that are usually missing in such explanations. Not only electron makes a “cloud”, but also a nucleus (a positively charged “cloud”, roughly speaking). The size of the latter is about me/MNan. For Hydrogen and for more heavy, but excited, atoms the positive charge cloud in an isolated atom can be larger than the nucleus proper size. Especially this thing is missing in picturing a solid crystal lattice – the electrons make overlapping continuous clouds, but nuclei are thought as still and well positioned points whereas they make positive clouds of the size comparable with the lattice constant. In other words, the plum-and-pudding model is more appropriate to picture molecules. Otherwise we make a smeared “photo” of the electron motion and an instant photo of the nuclei positions.
Regards,
Vladimir.
You’re correct of course, at a certain level; but the problem here is that really the quantum mechanics wave function of, say, 100 atoms of carbon in a diamond is not a function of space, but rather a function of (at least) all possible positions for the electrons and carbon nuclei — 2100 dimensions. What is done in defining a “cloud” is a projection of that function of 2100 variables onto the three dimensions of space… and in doing so, a lot of information is lost. Even when you simply put a hydrogen atom in a box, you have this problem. So there is a lot of murkiness in even defining these “clouds”, if you look too carefully; you have to decide what question you are asking and why you are asking it, which means there is an art to choosing the question, even though the answer is pure science. I do not think it helps the non-expert to know these details, most of the time. And an expert had better understand this backwards and forwards… there’s not much middle ground.
Yes, a wave function has many arguments, but there is a clear physical context in speaking of a 3D charge clouds – it is an elastic picture (elastic cross section). There the wave function is integrated to yield an elastic form-factor f(q) that depends only on a 3D transfered momentum q and is directly related to the 3D “charge density” rho(x), if Fourier transformed.
How the total number of electrons determine that 2 atoms of 2 different elements with same number of outer shell electrons have totally different chemical properties if the later is depending on the former in all reactions ?
The mass of the atom matters too; certainly Hydrogen behaves very differently from Potassium because of this, even though they both have one outer shell electron.
The energy levels of the different orbitals also differ – i.e. the single outer electron in Potassium is more reactive than than the outer electron in hydrogen, etc…The larger the atomic number, the farther out the reacting orbitals are, so their reaction energy is different.
I’m oversimplifying a bit, but the principle is true ( the electrons that are farther out see less positive charge from the nucleaus, so they are more weakly held onto the atom, etc…).
nucleus, that is…
Is it permitted to assume that there must exist an ultimate fundamental ” thing ” of which all of what we see of the fundamentals are modes ?
strings or something else , is it allowed by our physics without any extra-physical assumptions —-extra dimensions for ex.—- ?
I don’t know what we should assume about things we don’t have any evidence of…
What is the physical meaning of ( the uncertainty principle “” prevents “” ) , what causal physical power the U.P. have ?
i mean , how it physically affect the electron or how the electron feels and obeys the U.P. ?
Good question. A more precise statement is that electrons (ripples in the electron field) have properties and behavior that assure they always obey this principle. The principle is thus not causal but a consequence of the properties of electrons (and other particles.) All particles, in a quantum world like ours, have such properties, which is why the uncertainty principle is so universally applicable.
To show how the principle arises from the properties of the particles and fields of nature requires doing a little mathematics, more than I can do here.
Henry Reich has a short video about the uncertainty principle (http://goo.gl/5CJfQ). He explained the issue with respect to waves (or wave pulses), their location, and frequency. I’m not sure why his point can’t be generalized to any object.
Location and velocity can’t both be known exactly. To know the exact location of something, it can’t be moving — and has no velocity — and to know the velocity of something implies that it is moving and has no exact location.
Is this a bad way of putting it?
It is a very intuitive way of putting it and in fact I believed it for a large part of my life. It works fine for explaining the principle on a basic level, but it is fundamentally wrong and will break down when faced with an inquiring mind. (One may ask for example if we couldn’t measure several past positions, use those to work out the velocity and thus be able to predict the present location exactly as d =vt.)
Right, but one can never be sure about a projection like that. Isn’t that the point of the uncertainty principle?
No. There is no uncertainty involved in the “uncertainty principle”. It’s an unfortunate historic name. The relationship between a position measurement and a subsequent velocity measurement is precisely defined in QM. The only “uncertainty”, in the English language sense, is the fact that QM calculates a probability of finding particular values when making an observation, instead of predicting a single outcome. This applies even to single measurements, it’s not something that only manifests itself when there are a pair of measurements.
As Matt states the uncertainty principle is not the issue in projections, it is far more fundamental than that. It is easy in physics to create a situation where a particle is emitted with an well defined known energy (Thus for massive particles an well defined velocity.) and forced to move in an exactly predictable manner. (One example would be shining UV of a specific frequency light on zinc metal, causing photoelectrons to be emitted that then pass through a magnetic field. An electron with a given velocity moving in a magnetic field of a given strength should have a perfectly predictable path. Instead we find an irreducible a mount of uncertainty as if the electron itself refuses to be completely certain.)
Einstein called it The Indeterminacy Relation.
Interesting example of an estimate to the order of magnitude of the size of an atom (an average atom, that is),
It reminded me of the famous Einstein 1905 paper on brownian motion (maybe, the least famous of the “Annus Mirabilis papers”).
With this article Einstein presented one of first elements of evidence that atoms do exist.
One of the conclusions of that article was an estimate calculated by Einstein of the average size of a molecule or an atom.
Kind regards, GEN