© Matt Strassler [October 9, 2012]
This is article 8 in the sequence entitled Fields and Particles: with Math. Here is the previous article.
In the previous article in this series, I explained that the particles of nature are quanta of relativistic fields satisfying Class 0 and Class 1 equations of motion. But what I didn’t say yet is that — fortunately — this statement is only approximately true. The real equations are always a bit more complicated, in such a way that retains this relation between particles and fields but allows for a much richer set of processes to occur, including the production of particles from the collision of other particles, the decays of some particles to other particles, and the scattering of particles off each other, as well as the formation of interesting objects such as protons and neutrons, atomic nuclei and atoms. I won’t be able to explain all of that in detail, but in this article I’ll start to give you a feel for how it works.
The key difference between the equations that I called “Class 0” and “Class 1”, and the equations that are really important in real-world physics, is that the real equations have additional terms that depend on two or more fields at a time, rather than just one. What I mean by this is the following: instead of a Class 0 equation for a relativistic field Z(x,t) that looks like
- d2Z/dt2 – c2 d2Z/dx2 = 0
real fields in the world have equations that look more like this
- d2Z/dt2 – c2 d2Z/dx2 = y’ Z(x,t)3 + y A(x,t)B(x,t)
where y and y’ are numbers (generally not larger than one), “Z” is shorthand for Z(x,t), and A(x,t) and B(x,t) are two other fields. Other possible terms that one might find appearing in these equations would be A(x,t)Z(x,t), or A(x,t)2 Z(x,t), or Z(x,t)2, or even A(x,t)d2Z/dt2, etc. Which terms are allowed and which are not depends on the details of the fields involved; the rules are straightforward but long-winded, so let me not go into that right now. Generally, we have learned from experiment (and understood from the theoretical point of view) that in nature
- any term which is not forbidden by a principle (such as conservation of electric charge or consistency with Einstein’s relativity) appears in the equations,
- but terms with many fields are usually very small and unimportant compared to terms with one, two and sometimes three fields (and terms with time or space derivatives are usually small too.)
Therefore in most interesting physical processes we can focus our attention on all the allowed terms with just one, two or three fields.
A little term-inology. The terms in equations that involve one power of a field are called “linear”; all the terms we saw in our Class 0 and Class 1 equations were linear. Terms that involve two or three fields are called “quadratic” or “cubic”; more generally they are called “non-linear.” All of the interesting phenomena in our world arise because of the non-linear terms — the interactions of fields with each other and with themselves — in the equations of motion. And we’re going to learn about one of them now.
Production of a New Wave from the Resonance of Two Others
To get a feel for how interesting things can become, let’s take three fields A(x,t), B(x,t), C(x,t), and to keep things simple, let’s imagine the A and B fields approximately satisfy Class 0 equations (and therefore have massless quanta) while the C field satisfies a Class 1 equation (and has waves whose minimum frequency is νmin and whose quanta therefore have mass m = hνmin / c2, where h is Planck’s constant). But we’ll also put non-linear terms in the their equations. Specifically, we’ll consider (with shorthand “A” for “A(x,t)”, et cetera, and with c the speed of light and y a number, generally not larger than 1)
- d2A/dt2 – c2 d2A/dx2 = y B C
- d2B/dt2 – c2 d2B/dx2 = y A C
- d2C/dt2 – c2 d2C/dx2 = (2 π νmin)2 C + y A B
[Fine Point: The reason I put nonlinear terms in all three equations is that it turns out it would be inconsistent to have non-linear terms in one equation without having them in the other two; energy wouldn’t be conserved, for instance. For the process I’m about to describe, we’ll only need to study the nonlinear terms in the C field’s equations of motion.]
Let’s see what can happen, given this set of equations, if a wave in the A field meets a wave in the B field. We can actually guess, if we look carefully at the equations themselves. Where there is a wave in the A field, then A(x,t) is non-zero in most of that vicinity. When waves in the A and B field overlap each other, then the product A(x,t) times B(x,t) becomes non-zero. Now look at the C equation: it says that changes in the C field over time and over space (the two terms on the left-hand side of the equation) are related to A times B (one of the terms on the right-hand side of the equation.)
- d2C/dt2 – c2 d2C/dx2 = (2 π νmin)2 C + y A B
So even if the C field is zero to start with, once A(x,t)B(x,t) becomes non-zero, then soon enough C(x,t) will become non-zero in the same region. In short, some sort of small disturbance in the C field will result from the meeting of the A and B waves.
Fine point: You could then wonder, once C becomes non-zero, whether the A(x,t) C(x,t) term in the equation of motion for the B field would cause a further disturbance in the B field. The answer is yes, but it’s an even smaller effect. We’ll ignore it for now, and later will learn why that was a good idea.
In Figure 1 is shown a wave with frequency ν in the A field (green) meeting a field with frequency ν in the B field (blue). [I’m taking the frequencies equal to keep things simple and symmetric; later we’ll see why all other cases in the end reduce to this one.] Click the figure to animate it. You can see how fast the frequency ν is by looking at the green wave and noting a vertical black bar that sits at one point in space and oscillates up and down with frequency ν as the green wave passes by.
Below them, in orange, is shown the product A(x,t)B(x,t); you will see that this product becomes non-zero where the two waves are overlapping. You can also see that it oscillates with time. If you look really closely, you’ll see (comparing it with the oscillating black bar that shows you how fast ν is) that A(x,t)B(x,t) oscillates with twice this frequency! This is important: keep it in mind. [More generally if a wave of frequency ν1 meets a wave of frequency ν2, their product will include oscillations of frequency ν1 + ν2.] One more thing: you notice that the oscillations of A times B aren’t moving right or left; they are standing in place. We’ll see why this is important in a moment.
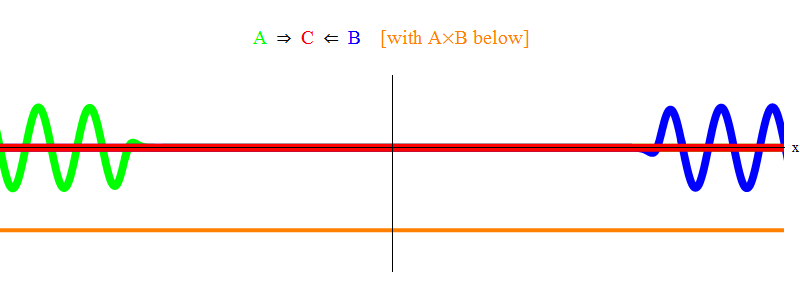
Now how does the non-zero value of A times B affect the field C? The answer depends on the frequency ν, in a very big way! Let me tell you the answer, and then I’ll give you intuition for why it is the case. It is basically a phenomenon of resonance. Resonance is an essential phenomenon for all types of oscillations (i.e. vibrations) including waves. I have previously described how a ball on a spring oscillates with a natural frequency, and described how an oscillating force pushing on the ball can cause resonance if the frequency of the force’s oscillation matches that natural frequency of the ball on the spring.
Once you do understand resonance, you’ll recognize that the C field, when it oscillates with minimum frequency and with zero velocity to the right or left (as described at the end of this article in the section on Class 1 waves — see Figure 2), is like the ball on a spring, and A times B acts like an oscillating force trying to make that ball oscillate (as described in my article on resonance.) And so there is a resonance phenomenon, if the frequency with which A times B oscillates — namely, 2ν — happens to be at the minimum frequency for the field C — namely, νmin. More specifically
- If 2 ν does not equal νmin — if the force is off-resonance — then, in the region where A times B isn’t zero, C will begin oscillating irregularly and with a small amplitude.
- If 2 ν = νmin — if the force is on resonance — then C will begin oscillating smoothly, with a large amplitude, in the region where A times B isn’t zero, and will continue to oscillate even when A times B becomes zero again.
Figure 1 only shows the resonant situation 2 ν = νmin. You see there that when the wave in A passes the wave in B, they leave a stationary C wave, oscillating at νmin, behind. [Fine point: what is shown in the figure is a sketch, and not the exact solution to the equations. The exact solution would have lots of additional small complicated feature, which would obscure the main physics point I am making, so for clarity I have removed them.] We will look at the non-resonant situation, which is more complicated but also physically important, at a later time.
Production of a New Particle from the Annihilation of Two Others
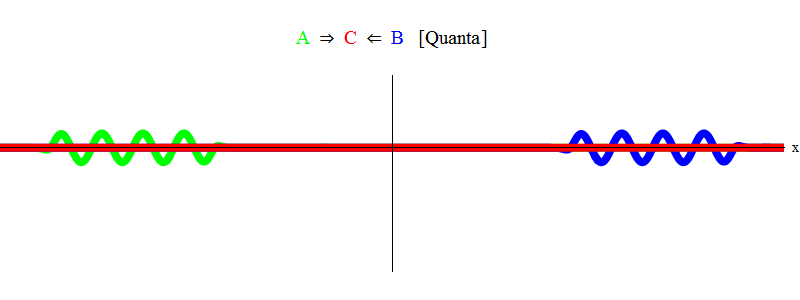
I’ve just shown you that the non-linear A-times-B terms in the C equation can cause two overlapping waves in the A and B fields to generate oscillations in the C field, if the sum of the frequencies of the A and B fields is equal to the minimum frequency for the C field. But what if these waves have very small amplitude to start with? What may happen if a single quantum of the A field meets a single quantum of the B field? (You can remind yourself about quanta here.) The answer:
- If the frequencies of A times B are on-resonance for the C field, then a quantum of the C field — a real C particle — might be created (and the A and B quanta will disappear — will be “annihilated”).
- Alternatively the A and B quanta may just pass each other and no C particle will be created.
- The laws of quantum mechanics imply that the probability for a C particle to be created in this situation is proportional to the square of the number y that multiplies A times B in the equation of motion for C.
- If the frequencies are off-resonance, however, a real C particle will not be created. There may however be a temporary disturbance in the C field, an example of what is often called a C “virtual particle”, in which case the A and B quanta may again disappear. What happens as a result of this disturbance? I’ve put in a little preliminary discussion of its implications at the end of this article, in the “Loose Ends” section.
Ok; that’s the general sense of things. Let’s go into a few details.
What does being on- and off-resonance mean for `particles,’ i.e., for the quanta of the fields A, B and C? The thing to remember is that the energy of a quantum is related to its frequency by the equation E = h ν. So let’s do a little translating of our wave discussion above into a discussion for `particles’.
Suppose that the waves in the A and B field that we started off talking about consisted of just one quantum each. Those quanta are massless since A and B satisfy Class 0 equations. [More precisely, the linear terms in their equations of motion are those of Class 0 equations.] Since the A and B quanta have equal frequencies, they have equal energies E = h ν. And since, for a massless quantum, its momentum has magnitude p = E/c, the A and B quanta have momenta that are equal in magnitude to h ν/c but are obviously opposite in direction, since one moves to the left and the other to the right. Therefore,
- the total energy of the two quanta added together is 2hν
- the total momentum of the two quanta added together is zero
Since energy is conserved and momentum is conserved, the total energy after these two quanta collide will still be 2 hν, and the total momentum will remain zero.
Now what we saw for waves is that because the equation for C contains a term of the form A times B, there is a resonance when the frequency of A times B (which acts like an oscillating force) matches the minimum frequency of C (which acts like a ball on a spring). Let’s translate this statement into quanta.
The frequency of A times B is twice ν, and so the energy of the product of A times B, when A and B each have waves consisting of a single quantum, is the sum of the energies of A and B:
- EAB = 2 h ν = EA + EB
The minimum frequency of C is νmin, which means a stationary quantum of the C field has zero momentum and energy
- EC = h νmin = mc2,
where m is the mass of a C quantum.
On-resonance requires 2 ν = νmin, or in other words
- EA + EB = 2 h ν = h νmin = mc2 = EC
In short, resonance occurs when the sum of the (equal) energies for the A and B particles (which in this case have equal and opposite momentum) is just the right amount to make a stationary C particle! Along the way, the A and B particles are annihilated — their energy is entirely used up in creating the C particle. This is shown [somewhat schematically — one can’t really draw what happens in quantum mechanics] in Figure 2, which you should compare with Figure 1.
Elaborations
I’ve just shown you the process A + B → C. I used three different types of particles in my explanation to avoid any confusion about what was going on. But the same basic idea allows for processes such as A + A → C (for instance, gluon + gluon → Higgs particle, the main way that Higgs particles are produced at the Large Hadron Collider) and processes such as A + A* → C, where A* is the antiparticle of A (for instance, quark + antiquark → Z particle, the main way that Z particles are produced at the Large Hadron Collider.) Only little details have to be changed; the basic idea is the same.
Another process that is basically the same idea, just reversed in time, is particle decay. The decay of a Higgs particle to two photons, or of a Z particle to a quark and an anti-quark, is basically the same as in Figure 2 with the animation run in reverse.
Some Loose Ends
1. If the A-times-B term pushes the C field off-resonance — if 2 ν ≠ νmin — what physical processes can result? You may recall (see my article on resonance) that if you push a child’s swing with the wrong frequency, or apply a force to a ball on a spring that oscillates with a frequency different from the ball-and-spring’s natural frequency, you will get a jiggly motion that is a bit messy and has small amplitude. In the current context, that’s what happens to the C field also. The C field will do something, but it won’t form a nicely behaved C quantum. It will just rattle around a bit. This ill-behaved disturbance is one example of what is called a “virtual C particle” — but it isn’t a particle (a quantum of a wave in the C field) despite the name. Its mass is different from the mass of a C particle; it may be much larger or much smaller. Unlike a C particle, it won’t exist on its own for any length of time. And it does not satisfy the condition on its amplitude that a real quantum must satisfy. Instead, unlike the C particle in Figure 2, which endures for a while, the off-resonance disturbance lasts only as long as the A and B quanta are overlapping.
But that doesn’t mean it can’t have any effect. For one thing, it could cause the A and B particles to bounce off each other
- A (to the right) + B (to the left) → C field disturbance → A (to the left) + B (to the right)
More generally, in three dimensional space, the bounce, or “scattering”, could leave the A particle traveling in any direction, with B traveling in the opposite direction. Examples of this process and its variants include the scattering of an electron and a positron through the effects of a virtual photon, or the scattering of a quark and an anti-quark through the effects of a virtual gluon. (There are many other scattering processes which are common but require a more subtle discussion; perhaps I will cover these at a later time.)
Or if there are other fields, D and E, that interact with C and also appear in C’s equation of motion
- d2C/dt2 – c2 d2C/dx2 = (2 π νmin)2 C + y A B + y’ D E
then a much more interesting process can occur:
- A + B → C field disturbance → D + E
That’s right: A and B particles can annihilate (via the C virtual particle) and a D and an E particle can be created in their place. This is a second way (the first being the one in Figure 2) that we can create new particles! For instance, an electron and a positron can collide, annihilate via a virtual photon (remember to read that language appropriately, as “via the disturbance created by pushing the photon field with an off-resonance frequency”), and become a muon and an anti-muon, or a quark and an anti-quark. A down quark and a up anti-quark can collide, annihilate via a virtual W particle, and turn into an electron and an anti-neutrino. Or two gluons can collide, annihilate via a virtual gluon, and turn into a top quark and a top anti-quark (this is the most common way to make top quarks at the Large Hadron Collider.)
2. What if the two waves in the A and B field had had different frequencies, νA and νB? C particles can still be created if the frequencies are right, but the resonance condition is different, and the C particle that is created won’t be stationary. Let’s work that out.
If they have different frequencies, the two colliding (massless) quanta would have had
- different energies EA = h νA and EB = h νB
- different momenta pA = + h νA/ c and pB = – h νB/ c (here the plus sign means “to the right”, minus sign means “to the left”)
The total momentum pA + pB is now non-zero. But momentum is conserved. So if a C particle can be produced in the annihilation of the A and B particles, it will have momentum pC = pA + pB, and thus it will be moving right or left, rather than stationary (as in Figure 2). (If νA > νB it will be moving to the right, otherwise it will be moving to the left.)
Now, how much energy is required to make a C particle that is moving? It requires more than when it is stationary, of course: as for any massive particle, its energy and momentum have to satisfy
- EC2 = (pCc)2 + (mc2)2
which says EC = mc2 if pC = 0, or greater if the momentum is non-zero. Energy and momentum conservation tell us
- EC = EA + EB
- pC = pA + pB = EA /c – EB/c
Where did I get the last equation? Well, for a massless particle p = E/c in magnitude, and for our colliding A and B particles their momentum is in opposite directions, so their momenta differ in sign (see above where we first discussed their momenta.) Now we substitute this into the previous green equation, and find
- (EA + EB)2 = (EA – EB)2 + (mc2)2
The EA2 and EB2 terms cancel from both sides, and pulling the EA EB terms all to the left-hand side we find the result
- 4 EA EB = (mc2)2
Dividing by h2 and using the relation m = hνmin / c2 gives us the resonance condition
- (2νA)(2νB) = νmin2
(which correctly reduces, if νA = νB, to the resonance condition for a stationary C particle, 2 ν = νmin.) If this resonance condition isn’t met, a C particle can’t be created; if it is met, then a C particle might be created.
3. I noted that just as the equation of motion for the field C contains a term A-times-B, the equation for B contains a term A-times-C. Let’s recall those equations:
- d2B/dt2 – c2 d2B/dx2 = y A C
- d2C/dt2 – c2 d2C/dx2 = (2 π νmin)2 C + y A B
So if the overlapping of A and B waves produces a new wave in the C field, making it non-zero, as in Figure 1, shouldn’t I worry that the overlapping of that new C wave with the pre-existing A wave will cause a change in the B field? And my answer was “yes, but we can ignore this.” We can ignore it for a combination of two reasons.
First, there’s the fact that the number “y” which appears in front of both the A-times-B and B-times-C terms. The effect on the C field from A B is proportional to y times the size of A times B. The effect on the B field from A C is similarly proportional to y times the size of the A times C, but that in turn is equal to y2 times the size of A times A times B. So as long as y is less than 1, y2 is less than y, so the effect on B from A C is therefore small compared to the effect on C from A B — well, at least if the waves in A and B aren’t too big. But in particle physics applications, the waves are generally small: an A particle is a single quantum of a wave in the A field, and so corresponds to A having a wave with a small amplitude.
Which leads us to the second, weirder but a bit more convincing, reason: In fact, as we saw, if a single quantum of A meets a single quantum of B and turns into a single quantum of C, the waves in A and B completely disappear (i.e., are annihilated.) So after C is created there actually is no A wave left, and therefore A-times-C is zero after all, meaning there’s no effect on the B field.
A final caveat: although I can’t prove this to you without more work, even if A and B have waves of just one quantum each, as in Figure 2, the process depicted in Figure 2 would be much more complicated if y were very large compared to 1. So the simplicity of the story that I have told you does require y not be too large; otherwise it has to be reconsidered. It happens in nature that most of the non-linear terms that arise in particle physics have small “y”, and so what I’ve told you is relevant for most particle physics applications. The exceptions are interesting — they lead to complicated objects like protons and other hadrons.


49 Responses
Prof. Strassler, thank you for everytihng, your page is brilliant. In case you still provide replies to older articles, I would like to ask a question about fields and their meaning for causality.
The fields interact with each other and particle physics undestands every such interaction as “bidirectional” – it can happen both ways with the same probability. However, no change in entropy is involved and no arrow of time can be determined under such reduced scenario. Once multiple particles are considered and the geometry of their “placement” in Spacetime (or the sum of information they express by the actual way They ARE in the universe) allows to deterrmine what was the course of interaction and which way the reaction went – allowing for entropy and time to make sense. The reality of the world includes (obviously) many particles. There are futher causal issues at play under such circumstances, namely the “spherical nature” and an (unlimited) extent of gravity + electromagnetic fields associated with charged particles. These tend to shape our worlds rather significantly as causal factors. Is it so that objects of rather unchanging number of fermions (such as the Earth) are primarily shaped by ever changing infuences of gravity and electromagnetism (including influences from other objects, namely the Sun. So is there any value of the structure of the matter as far as fundamental laws of physics are concerned and are there any means of theoretical physics to dealing with such issues. Sorry for the layman’s language. I was wondering if you could elaborate on the theme of causality.
Arena of physics bast on a belief: simplicity being the law of the universe. But why should the fundament of the universe be simple? Because the observation too limited and test too partial. If this be a faket corner of a complex universe, the tendency will be wrong and the laws be local and phenomenon, like the pure linear field equation here.
And why should there be more laws than irregularity? Maybe only because the sample pool too small and neuronal evolution path force it to create continuously such a delusion, or the arena of physics.
I have some doubts on particles, fields interaction. My current understanding says that, fields(virtual particles related to the field) carry momentum of the source particle and interact with other particles..but what I don’t understand is, when will the source particle lose this momentum that is carried by this virtual particle? is it like after sometime, if this virtual particle interacts with something, then instantaneously the source particle loses momentum? or even before when this virtual particle interacts with something else?
basically what happens to the particles kinetic energy when the field related particle is interacting with something else?
All in all, i don’t quite understand how field manages momentum transfer, like when the particle k.e changes etc.
I may not have been clear above, would be great if these can be explained properly. i.e the field and particle interaction process, as close to reality. with a scenario like a 3 particle interaction or 2 particle interaction.
Thank you.
Is there any significance to the fact that the A & B waves have constant amplitude as the interact in fig 1 but leading edge decreasing amplitude in fig 2?
This stuff is great. I’m curious — what do you use to create the animated diagrams?
Thank you! It’s just Mathematica.
Thank you for a very clear presentation that chose the right level of complexity. It would be great to read
a followup article that shows how (for instance) two electrons interact using photons to create the electromagnetic
force. With explanations of how the force is a function of 1/(R*R) and how the potential energy of the fields is
converted into the kinetic energy of the accelerating electrons.
Hello prof. Strassler, and thanks for this very useful series.
Probably much too late, but I have a question that goes back a few in the series, is probably not needed for what you are trying to explain, and comes from someone with less physics than most here, but has done math, quite ‘pure’, for a long time. Simply put, the question is just what sort of mathematical ‘species’ does one have at each space-time point in one of these fundamental quantum fields, e.g. the electron field, or the top quark field, or the photon field, or the Higgs field?
I’m not embarrassed if this question turns out to be meaningless, and I’m not necessarily asking for details of a physical interpretation of that mathematical object, but let me explain the question just a bit more below.
The classical ‘practical’ examples of fields you first gave, like air pressure, were mostly scalar fields, so there the answer would be ‘scalar’ (or ‘real number’). For vector fields, it is ‘vector’ (or perhaps ‘tangent vector’ or ‘cotangent vector’). For the classical fields of Maxwell and Einstein, the answer would be ‘tensor’ (most would understand, though still a kind of vector to a mathematician, being a tensor built from the previous tangent and cotangent vectors). But for the quantum fields of the particles of the Standard Model, I haven’t seen the answer to this, though I’ve superficially read parts of Peskin-Schroeder, and more thoroughly gone through various writings of Penrose. I’m well aware that there is a ‘language barrier’ between many mathematicians and many physicists.
My vague guess is that in each case there is a classical ‘sort of version’ with some kind of tensor field (i.e. Maxwell tensor field for the photon) which is then quantized, so that the corresponding quantum field is a ‘complex separable Hilbert space vector field up to scalar indeterminacy’ in some sense. But I’ve never seen this explicitly stated anywhere; I may be completely off-base here; and it is likely not really relevant to what you want to convey, as I mentioned above.
i am so gratefull for these articles. i have the basic essentials but this is the first time I was able to see the big picture.
Is it appropriate to say that if C is a mixing product of waves A and B there could be more mixing products coming from not only from A+B, A-B which are the second order mixing products, but also the third order terms 2A*2-B, 2A*2+B, 2B*2-A, 2B*2+A and so on… do they come into play at some point? this requires nonlinear interactions with large field amplitudes, which are enhanced by resonsance condions (as stated).
any comments?
Thanks for the great article, Professor.
A couple of typos:
“nu;” I think you left out an “&”
“term-inology” These is an extra “-“
I have found your blog to be very clear and informative and I have a question about this article.
What determines the “lifetime” of particles created by the meeting of quanta?
In Figure 1 you show two waves passing each other causing A x B > 0 while they are overlapping and then when they finish passing each other A x B = 0 and C goes back to zero as one might expect from looking at the equations. However, clearly this isn’t the only case as you have described a scenario where two particles from one field meet and form a third stationary particle (that doesn’t disappear) in another, causing the annihilation of the first two particles. So in short, I was curious about what determines what kind of behavior is observed. (Does it have to do strictly with the equations of motion?).
I am wondering about one example from this article: “A down quark and a up anti-quark can collide, annihilate via a virtual W particle, and turn into an electron and an anti-neutrino.”
This process looks like beta decay (neutron into proton+electron+antineutrino). Is this how it happens?
Indeed, my reply left a lot out of virtual particles, which as you say are a complex area of physics in and of themselves. I think perhaps the ‘particle’ part of the label causes me to limit in my mind what they are.
In this article series, the essential difference between classical and quantum waves has been that quantum waves have a quantized energy spectrum while classical waves have a continuous energy spectrum. Since virtual particles aren’t quantized, what is the difference between virtual particles and classical waves?
Virtual particles are quantized, however they lack the clear, well-defined mass or frequency of a real particle. A virtual particle can have any mass, energy or frequency it wants, but it is still *a* virtual particle.
A classical wave could continuously excite the electron field for instance, until enough excitation had occurred to produce an electron, a virtual particle either can or cannot produce an electron, depending on how much energy it has. This is very much like the photoelectric effect that lead to the development of quantum physics.
“Virtual particles” (which really aren’t particles at all) in quantum field theory are a very complicated subject; it’s not really one topic, except to the mathematics. Meanwhile, even classical fields can do much more than just “wave”. So I am afraid this is not something that has an easy answer. There are situations in which virtual particles are similar to classical field deformations; for instance, an electric field that forms inside an atom is due to “virtual particles”. So are the quantum fluctuations of the vacuum. And so is the state of the Z-particle’s field that allows an electron and a positron to annihilate to form a neutrino and an anti-neutrino. All this is to say is that real particles are relatively straightforward: an electron is an electron. But a “virtual photon” is really a stand-in for the full diversity of what the photon (i.e. electromagnetic) field can do, and that includes a huge variety of things, some of which is related to classical fields and much of which is not.
At some point you really *do* have to learn quantum field theory, and I’m afraid a proper understanding of virtual particles requires it.
The process is pretty much the same yes.
Imagine a child on a swing that you are pushing off-resonance, you can never get the swing to settle into a nice, stable motion, it keeps losing energy and motion. If you stop pushing the swing however it will quickly settle into a stable, resonant motion by shedding energy. (In this case it is creating waves in say the pressure field, that is, sound, and other fields.) This is like a virtual particle decaying into particles in other fields.
If another child on a stationary swing is nearby it is possible for the off-resonance child to bump into them, transferring energy until both swings are ins table (And non-interfering) motion. One virtual particle has decayed into two stable ones.
Thanks so much!
When electron and positron annihilate at low energies, they produce 2 photons. How are these 2 photons created? During the annihilation, the positron and electron disturb the electromagnetic field off-resonance, because there is a reference frame where the net momentum is zero. But then somehow 2 real photons escape (with the net momentum still zero, of course). Are these 2 real photons somehow rising from the virtual photon? So the off-resonance disturbance can “decay” into real particles?
That is correct and it is how a lot of particles are created. One of the defining traits of ‘virtual particles’ is their instability; they rapidly disintegrate into ripples in other fields, hopefully ending in stable or relatively stable particles.
Thank you. Just a small detail: this time it is not virtual particle disintegrating into ripples in other fields, but virtual particle disintegrating into ripples in the same field (virtual photon into real photons). I noticed that Professor Strassler avoided that case (virtual photon into real photons) in the text and rather described other process (virtual photon into real fermions). I’m not sure if it was intentional (because “virtual photon into real photons” is somehow different process), or it just does not matter and the process is the same. But from your response I feel it is just the same process. The only thing I’m not sure I understand is how the off-resonance disturbance gives rise to resonant events inside the same field.
It happens that a virtual photon does not easily turn into real photons, but that has to do with the details of what photons can and can’t do. It can happen, but it requires other virtual particles to get involved.
A virtual gluon can most certainly and easily turn into two real gluons. Same with gravitons.
So it’s not a matter of principle; just a detail of what the individual types of particles do and don’t do. Even more precisely, it is a detail of exactly what types of equations individual types of fields satisfy, which determines the types of processes their quanta can participate in.
you’ve left something out; they may also annihilate with other virtual particles or combine with other virtual particles to form real ones.
Also, I wouldn’t use “hopefully” here.
Virtual particles are a very big subject; they do many different things, which is why giving them a single name and associating them with “particles” is somewhat unfortunate. There are good mathematical reasons in certain calculations for treating them together, but conceptually it’s really a very complex subject… which is why I call them “disturbances in fields that aren’t particles” and usually try to avoid going into too much detail.
Sorry, I started reading your post on the known elementary particles and realized that in your example of a virtual W particle you are talking about Beta Decay, which I don’t pretend to understand in any great detail, but now doesn’t seem odd anymore.
You wrote:
A down quark and an up anti-quark can collide, annihilate via a virtual W particle, and turn into an electron and an anti-neutrino.
Am I supposed to be able to follow this because frankly I don’t. I believe you! and maybe it just sounds a little more odd than the creation of a muon and anti-muon from a virtual photon. I imagine that an electron and an anti-neutrino conserve whatever has to be conserved but I don’t consider that “following” you. If you have an FAQ which explains this, please tell me which one! Thanks.
The above comment by thetasteofscience seems to be in response to my observation about the unprintability of this thread, so I will reply to it.
I have a background in graphic arts, so I know there are various workarounds to the problem such as pasting the contents into Word. The one I have used for this case is taking a series of screen shots and printing those. This is easier on a Mac than a Windows box. But still so much more laborious than having the file work properly in the first place.
I should also say that some threads do work properly. The recent post, Quantum Physics is Very Real is an example. Clearly, there is a bug or glitch in a few of Professor Strassler’s pages. Fixing them would probably involve starting with a template that has proven to work. Then pasting a chunk at a time and testing after each addition to find the cause for the loss of printability.
Many thanks again for the fascinating and educational content.
I like having personal copies of these articles, in which I find so much of value, so I copy them into a Word file and can then annotate, print them etc. I don’t find this particularly hard to do.
As long as all the conservation laws are met then particle C *may* be created. Think of particle decays, the reversed process. Few particles are standing still when they decay, but it still works. Likewise, the overwhelming number of cases of particle creation will involve two particles whose total momenta is not zero and whose energy large enough to make a moving particle C.
Amplitude doesn’t come into this because we’re dealing with single quanta; the smallest possible amplitude. (In our case it goes from 1 to 0 as both quanta disappear.)
If the two waves A and B in Fig 1 had too much energy too be “on resonance” with 0 net momentum but had different momenta(as in direction not magnitude) will they create a new particle in C if conservation of momentum is met?
Also I presume the frequency in A and B drop when they create resonance in C?
How come amplitude doesnt seem to come into this as well?
Amplitude does come into it — when he specifies a single quantum of A and a single quantum of B, that’s a specification of amplitude. If you go back to part 5, you’ll recall amplitude is proportional to the square root of the quantum number (n).
If I may, I would like to ask 2 additional questions:
1) How can a photon field be disturbed off-resonance? I am referring to the process when electron+positron disturb “virtual” photon which creates something else (like a quark pair). Photons are massless, so they don’t have any restrictions on frequency. So it seems that any excitation in electromagnetic field should be on-resonance.
2) How can 2 different quanta be created from a virtual particle? From the math it seems they cannot, because the product of the source fields seems always zero. Let’s say we have a virtual particle in C field and it interacts with D and E. The equations for D, E would be:
Changes in E(x,t) over x and t = y C(x,t) D(x, t)
Changes in D(x,t) over x and t = y C(x,t) E(x,t)
We begin when D and E are zero (or are they? I’m not sure what the “zero point energy” can do here). If the C(x,t) is disturbed, none of the terms C*E or C*D will be greater than zero, because E is waiting for D to become non-zero and vice versa.
This would work only if there is a term like this:
Changes in E(x,t) over x and t = y C(x,t)
Then E(x,t) would be disturbed by only C(x,t), without E waiting endlessly for D to be disturbed. Is that the case? Maybe my questions are just horribly silly, in that case I apologize.
I think for your question 1) conservation of momentum has to be met. With massless particles their momentum is proportional to their energy, so they cant be resonant with certain energys as this energy gives more or less then the positron + electrons momentum.
Which raises the question about what happens when an electron and positron have 0 net momentum, is a photon never produced? So annihilation doesnt always happen?
It would be very difficult to have a situation where two particles can approach each other and yet have zero momentum, especially particles that interact as strongly as the electron and positron.
But they would still annihilate; two photons of equal energy traveling in opposite directions have equal and opposite momenta, for a total momentum of zero. This is covered on the particle decay page, where it is noted that decays to (And thus combinations of) three, four or more particles are possible, so long as their total momentum is the same as the initial momentum. (Decays to three or more particles rapidly become incredibly rare of course.)
1. photons have no restriction on their frequency, but their frequency and their wavelength are always related — so their energy and their momentum are always related. It was very important in what I was explaining to you that particle C was stationary — its momentum was zero. (See the discussion at the very end about cases where the momentum isn’t zero.) The only photons with zero momentum have zero energy. Conversely, photons with non-zero energy always have non-zero momentum. Therefore, it is impossible to make a photon as a resonance through a collision of two particles of finite energy.
2. An excellent insightful question. The way it works is tricky, and that’s why I didn’t explain it, but you were right to notice the inconsistency. The point is that quantum fields are never strictly zero, for the same reason that the quantum ball on a spring is never really at rest — they are always jittering, and always have zero-point energy. http://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/ball-on-a-spring-quantum/ (and see also http://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/5-waves-quantum/, especially the figure which attempts vaguely to illustrate this.) Because of that, it is possible for the quantum of C to combine with the zero-point jitter of E to allow E to become non-zero.
Thank you very much for the answer.
How typical is it for frequencies of A times B to be on-resonance for the C field? Somehow I’m thinking that in most situations they happen to be off-resonance, so most interactions result in a virtual particle disturbance. Is this true?
Yes, this is correct. To make Z particles in electron-positron collisions, such as was done at the LEP collider, required tuning the electron and positron beam energies to be just right. In the proton-proton collisions of the Large Hadron Collider [LHC], most collisions of two gluons do not have the right energy to make a Higgs particle. That is one of several reasons why the production of a Higgs particle in a proton-proton collision is very rare.
A brilliant article, especially the animations.
You’re too kind… but I am glad you like it.
When trying to print or save this article as a pdf, the left half of the page gets chopped off.
Your efforts in writing this stuff is greatly appreciated. It would be nice if it were possible to save and print hard copies so as to save the strain of trying to read a computer screen.
Thanks.
Hi Matt,
Love your blog. But I had a question about your presentation of quanta, both for single oscillators and for fields. (Some of this discussion refers back to Ch. 2 — http://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/ball-on-a-spring-quantum/)
Energy eigenstates do not oscillate, and do not correspond to classical oscillations of definite, quantized amplitude. After all, the energy eigenstates of a harmonic oscillator are stationary states — all their observables are time-independent.
I think you may instead be referring in Ch. 2 to coherent states, which, as you know, are eigenstates not of the Hamiltonian but of the annihilation operator. Coherent states are therefore insensitive to quantum-mechanical perturbations (whose time evolution is loosely modeled by hitting the state with an annihilation operator to extract one quantum of energy), and one can easily show that coherent states saturate the uncertainty relation and are Gaussians in both position space and momentum space; in position space, their Gaussian wave-functions literally oscillate in time at the oscillator’s classical frequency omega. Those are the quantum-mechanical states that correspond to classical oscillation modes, and if you ask how many quanta they contain, the answer is n with probability P(n) given by the Poisson distribution.
But their classical oscillatory amplitudes are definitely not quantized. The oscillatory amplitude of a coherent state is determined by the real part of the eigenvalue under the annihilation operator, and it can take any real value at all. The ground state of the oscillator is, in particular, a coherent state that doesn’t move at all (it’s the only state of a harmonic oscillator that’s both a coherent state and an energy eigenstate), and it appropriately has vanishing oscillation amplitude.
The connection between classical oscillatory modes and their associated quanta is therefore very subtle, and does not admit an intuitive classical explanation. States with a definite nonzero number of quanta are not coherent states, and all coherent states that are not the ground state have an indefinite number of quanta in them. The same is true for classical fields, which are, after all, just an infinite collection of harmonic oscillators in Fourier space (in the free-field limit of vanishing interactions).
In particular, any classical superposition of field coherent states is still a coherent state, so you can’t make a state of a definite nonzero number of the underlying quanta just by classically superposing fields. (To make a classical superposition of coherent states, you hit the ground state with multiple displacement operators ~exp(amplitude*creation_operator). That’s different from making a quantum-mechanical sum of two different state vectors.) A classical wave of definite frequency does not have quantized amplitude, and does not correspond to any particular definite number of particles. (The probability P(n) of getting n particles is again given by the Poisson distribution.)
Of course, in certain contexts, solitons of a nonlinear field theory do become particles in an appropriate limit (such as in electric-magnetic dualities), but the new particles are not the underlying quanta of the original fields — they become the quanta of new fields after performing the duality transformation.
Please let me know if I’m mistaken in this analysis — I’m very interested in hearing your thoughts.
This is all correct.
However, in any pedagogical presentation one has to decide what compromises to make, and certainly this article and the ones preceding it are not intended for those who are learning quantum mechanics at a technical level, where indeed the detailed “murkiness” of wave-functions, creation and annihilation operators, superposition, coherent states, expectation values, etc. has to be introduced and understood with care.
The goal of these articles is to create for the reader a useful set of intuitions which, though imperfect at a technical level, will mislead the reader relatively rarely, and will allow the reader to grasp aspects of very subtle subjects, such as quantum fields, quanta, zero-point energy, virtual `particles’, and the like.
So while what you say is true, it would not be helpful, in my view, to deal with it here. I have tried to make clear that I am making compromises in my presentation, for instance by reminding readers in figure captions that one cannot really draw what is happening in quantum mechanics (such as figures 1 and 3 of http://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/ball-on-a-spring-quantum/ ) I think the introduction of coherent states, or more likely, of wave functions for stationary states, would be conceptually so confusing as to make it impossible to understand how the things we call particles can be quanta.
I very much appreciate the kind and well-reasoned reply. Thanks!
“Which terms are allowed and which are not depends on the details of the fields involved; the rules are straightforward but long-winded, so let me not go into that right now.”
Oh, I would love to see those. Especially if they involve real fields; one rarely gets any information on those, especially when reading press releases.
I hope you will put all this into a neat package (PDF?) when you have completed it. It is great!
I agree it would be very usefull to have all that sequence in a pdf.
Someday it will likely be a book, but not soon.
This is an awesome article, it tells a lot of interesting information. Thank you!
I wanted to ask about the situation when just 1 quantum in 1 field is involved and it interacts only with 1 other field: for example an electron disturbing the electromagnetic field. Like in your article about the virtual particles, where the “less naive” view of electron is introduced: electron which is also partially a disturbance in the photon field. Is this governed by the linear or non-linear terms in the equation of the photon field? I’m assuming it is non-linear (because you said that all interesting phenomena arise from the non-linear terms :-). I just don’t completely understand the difference between the thinkable equations, like this: d2A/dt2 – c2 d2A/dx2 = y E(x,t)
… or this: d2A/dt2 – c2 d2A/dx2 = y E(x,t) A(x,t)
… or this: d2A/dt2 – c2 d2A/dx2 = y E(x,t)^2 A(x,t) … this has the non-linear term, I suppose…
All these equations tell the photon field A(x,t) to be disturbed by an electron – a wave in E(x,t). Which of these right-hand-side terms contributes the most to the effect of electron disturbing the photon field? I would say the first one, because it is simple and does not get squared (and thus diminished, since small field squared is even smaller field). But your comment was that the non-linear terms are important.
And what is the difference between the first and the second equation? Multiplying the E(x,t) by the unknown function A(x,t) must have some impact on the solution A(x,t), but I’m not such an expert on partial differential equations to be able to say what impact exactly.