© Matt Strassler [August 28, 2012]
This is article 2 in the sequence entitled Fields and Particles: with Math. Here is the previous article.
In the previous article (Ball on a Spring [Classical]), which you should read first, the key results were that oscillatory motion of a ball on a spring, in the pre-quantum physics of Newton and his friends, takes the form
- z(t) = z0 + A cos [ 2 π ν t ]
where
- z is the position of the ball as a function of the time t
- z0 is the equilibrium position of the ball (i.e. where it would sit if it were not oscillating)
- A is the amplitude of oscillation (which we are free to choose to be as large or small as we want)
- ν is the frequency of oscillation (which depends only on the strength of the spring K and the mass of the ball M, and does not depend on A)
Also, the total energy stored in the oscillation is
- E = 2 π2 ν2 A2 M
By adjusting A as we wish, we can store any amount of energy in the oscillation.
In quantum mechanics, things change. At first glance (and that’s the only glance we need, really, but I’ll say a bit more in a moment) there’s really only one thing that changes, and that is the statement that “we are free to choose [the amplitude] to be as large or small as we want.” It turns out this isn’t true. And correspondingly, the energy stored in the oscillation cannot be chosen arbitrarily.

Quantization of the Amplitude of Oscillation
Max Planck, the famous turn-of-the-20th-century physicist, was the one who discovered that there was something quantum about the universe, and he introduced a new constant of nature, called Planck’s constant, h. Every time you see something in quantum mechanics, you will see h appear. (Quantitatively, h = 6.626068 × 10-34 m2 kg / s — tiny in the units of ordinary human life.) And here we go:
The quantum ball on a spring can only oscillate with amplitude
- A = (1/2 π) √ 2 n h / ν M
where n is an integer, i.e. 0, or 1, or 2, or 1798, or 2,348,979, etc. Oscillation is not arbitrary, it is quantized: and we may call n the number of quanta of oscillation. (Singular: quantum; plural: quanta.) And a definition: we will say that a ball oscillating with n quanta is in the nth excited state; if it has zero quanta we say it is in its ground state.
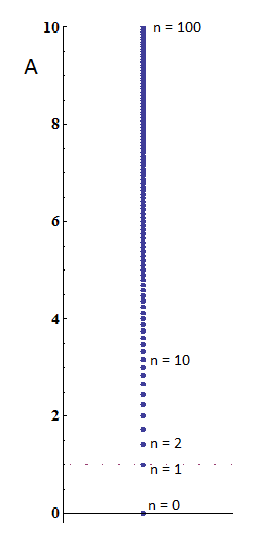
To give you a sense for what this means, the first five excited states, and the ground state, are (very naively — don’t take the picture very seriously!) illustrated in Figure 1. Note the smallest possible oscillation is the n=1 state. That’s one quantum of oscillation; you can’t have a fraction of a quantum. The ball cannot oscillate less than this, except to be in its non-oscillating ground state, n=0.
Otherwise things are (at first glance) pretty much the same. To be sure, the story of quantum mechanics is quite a bit murkier than just this! But we can get the physics basically right while skirting the murkiness of quantum mechanics for now.
Now why can’t we easily tell that oscillation is quantized? Because in systems of daily life, the quantization is far too small. For a realistic ball and spring — let’s say the ball has a mass of 50 grams (about 1/9 of a pound) and the frequency of the oscillator is once per second. Then an oscillation with just one quantum (n=1) corresponds to the amplitude
- A = (1/2 π) √ 2 h / ν M = 1.8 x 10-16 m
That’s a couple of ten thousandths of a millionth of a millionth of a meter, or about 10 times smaller than a proton! A single quantum of oscillation wouldn’t even make the ball move by a distance of an atomic nucleus! No wonder we can’t observe this quantization!! If the ball moves an amount that we can see, it has an enormous number of quanta of oscillation — and for such large values of n, we can make A be anything we want, as far as we can tell; see Figure 2. We can’t measure A nearly well enough to notice such fine restrictions on its precise value.
Comment: Notice this is partly due to the huge mass of the ball. If the ball were made from 100 iron atoms, and about a thousandth of a millionth of a meter in radius, its minimum amplitude of oscillation would be about a millionth of a meter, i.e. a thousand times larger than the ball’s radius. That’s big enough that you could observe it with a microscope. But such a small ball, subject to typical atomic-scale forces, would also typically oscillate much more often than once a second, and higher frequency would mean lower amplitude for a single quantum of oscillation; so even with a smaller ball, it’s still not so easy to detect the quantization of nature.
Quantization of the Energy of Oscillation
Now let’s take the quantization of the amplitude, and put it into the formula for the energy of oscillation that we had at the very start of this article, E = 2 π2 ν2 A2 M. Plugging in the allowed values for A from our red formula above, we find an amazing result
- E = n h ν (naive!)
a remarkably simple answer! The energy stored in an quantum ball-on-a-spring is (naively) proportional to n, the number of quanta of oscillation, times Planck’s famous constant h, times the frequency ν of the ball-on-the-spring. Even more amazing, this simple formula is almost correct, too! What’s correct about it?
- the energy required to increase the number of quanta in the oscillator by one (n → n+1) is h ν.
- in any oscillator we’d encounter in ordinary life, a single quantum of energy is so small that we’d never know energy was quantized.
[Let’s check the last statement. For a ball and spring that oscillates once per second, a single quantum of energy is 6.6 × 10-34 Joules, i.e. 0.000,000,000,000,000,000,000,000,000,000,000,66 Joules. And a Joule is about the energy you would exert in raising an apple from the ground up to waist height… not that much to start with! So this is an astonishingly tiny amount of energy. Only in small molecules, and even smaller systems, can the frequency of oscillation be so large as to allow the quantization of energy to be detectable.]
It turns out that our energy formula isn’t entirely right. With a real quantum mechanics calculation, one finds that the correct formula for the energy is
- E = (n + 1/2) h ν (correct!)
We won’t often need to pay attention to that little shift of n by 1/2. However, this shift is very, very interesting — it’s where all the murkiness of quantum mechanics starts. Isn’t it curious? Even when there are no quanta of oscillation in the oscillator at all — when n = 0 — there’s still some amount of energy in the oscillator. This is called zero-point energy, and it is due to a basic jitter, a basic unpredictability, that is at the heart of quantum mechanics. (See Figure 3 for a [inevitably schematic and inaccurate] picture that attempts to illustrate how the jitter is responsible for the zero-point energy; note the ball moves around randomly, even in the ground state.) And we’ll get back to the zero-point energy at some point later… because it will lead us to some of the deepest problems in all of physics.

Quantum Mechanics: Into the Murk [under construction, and not our first priority]


78 Responses
Please correct equation for relationship between A and energy E (should have sqrt(1/nu^2…)
Isn’t it known that things are quantized because electron orbitals require an integer number of de Broglie waves, thus the photons they’re capable of emitting (absorbing) on orbital descent (ascent) are quantized, thus the energy of those photons is quantized, thus the zero point energy field primarily contains that entropied energy of wavelengths corresponding to those energies of those photons emitted?
Had symmetry breaking of the Unified force into gravity and the electronuclear force, which symmetry broke into the strong and electroweak forces, which symmetry broke into the weak and EM forces never taken place, then energy wouldn’t be quantized, as composite particles would never have formed.
The non-quantized energy from prior to this symmetry breaking must still exist, but because electron orbitals can only absorb in quanta, it never gets utilized via vacuum polarization to sustain electron orbit (reference Boyer et. al., 1975) unless it red-shifts due to universal expansion.
Since E = (n + 1/2)h{nu}, then as you stated, it takes h{nu} to increase the quanta of an oscillator. So a 1Hz oscillator takes 6.6*10^34 J/s to increase 1 quantum. An oscillator of .999Hz would then take 6.5934*10-34 J/s to increase 1 quantum. The energy is quantized but the frequency doesn’t appear to be. So for any given oscillating system its energy increases by h{nu} but there is a continuous spectrum of frequencies available? If so, then with no lowest quantized frequency there would be no lowest quantized energy increment?
If figure 3 animation is inaccurate but you chose it, does this mean no more accurate representation is possible?
A motivating discussion is definitfely worth comment. There’s no dolubt that that you need to
write more on this topic, iit may not be a taboo matter but generally folks don’t speak about such topics.
To the next! All the best!!
Do you still believe spacetime is not quantized?
Thank you for another informative blog. Where else could I am getting that type of
info written in such an ideal method? I’ve a venture that I am just now operating on, and I’ve been on the glance out
for such info.
I want to to thank you for this fantastic read!!
I certainly enjoyed every bit of it. I have got you bookmarked
to look at new stuff you post…
Kevin is right
You are a saint, professor, or at least have the patience of one!
Did all the constants of nature, c, h, e-, muo, eo, etc. have the same value throughout all the expansion of the universe. Were they always constant AND have magnitudes we measure today or could they have been different in te early universe, smaller planck constant, faster speed of light, etc.
See http://profmattstrassler.com/2012/12/18/the-constancy-of-the-heavens-verified-anew/
I’m unable to activate the animations in these articles. Can you please provide instructions?
Otherwise, super-excellent website.
Hi, I can not get this formula (A = (1/2 π) √ 2 h / ν M = 1.8 x 10-16 m) to come out correctly. I get the value of 2.59106358983067E-17. That was using (1 / (2*π) ) * (√( (2*n*h) / (v*M) ) ). I used v=1, n=1, M=0.05 kg, h = 6.626068E-34 and π = 3.14159265358979. What am I doing wrong? Thanks, Dale
I’m really looking forward to the section “Quantum Mechanics: Into the Murk” which is now under construction.
TL;DR
Prof. Strassler,
Thank you for your very significant reply to my last post and the time you devote to this public education project. It is rare to see such a blog and the personal commitment of a professional to the course of finding the truth about nature and sharing that struggle through the bumpy road it has been for thousands of years.
I wish to address your points a bit out of order by starting with your comment:
“So I hear your nice words, and I think: does this man have any experience with equations? Has he seen how badly things can go wrong when we calculate things that sound nice but don’t, on careful examination make sense?”
Yes, I do have experience regarding your so very pertinent statement. My experience doesn’t come from my own flops at doing calculations that are beyond my training, simply because I almost never attempt to do any math beyond my education. But I have seen others, and I’ll bet you have as well, who have done pages full of formula and calculations and then describe what it is about and then you realize that they don’t in fact understand the field of knowledge that they are applying their mathematical abilities to.
One of the lessons I have learned from history is that there is an abundance of information and perspectives learned on one’s own, and with the help of good science writers, that helps make sense of the world that does not involve talking about precise definitions of physical quantities and using mathematical formulas. To be specific I will reference Stephen J. Gould, who was the top contributor to Natural History magazine, and one of my favorite scientists. I used to read that magazine every month for many years. I can assure you that those essays did not lead the readers nowhere. The mathematical world you inhabit as a particle theorist is not the same necessary world all investigators of nature need to be in.
While not having been schooled in higher mathematics is a huge setback for me personally since I love science, it hasn’t prevented me from learning of, and comprehending many important concepts in physics. In fact, as an example, I discovered individually, because of my own thought experiment, a full year before Lev Okun’s “The Concept of Mass” article in Physics Today in 1989, and before learning of Carl G. Adler’s paper “Does mass really depend on velocity, dad?” in the Am J. Phys., August 1987, that mass does not increase with velocity. (Proof is in my three binders of my correspondences that I have neatly organized.) I did not use and did not need correct mathematical formula and calculations to find out that so much of physics teaching at the time was incorrect in this matter. Needless to say, I was very excited when I discovered Okun’s article.
Contrary to many science writers who claim otherwise, I can also visualize in my mind the absolute and relative nature of time and space and the warping of space-time by massive objects and by accelerating frames of reference. I don’t need precise quantities and mathematical formula to lead me to make sense of these things. If interested please see my essay, “Why Time is Absolute, and Relative, But Never Universal.” Clicking on my underlined name will take you to the front page of my website critical of Big Bang cosmology. Scroll down to find the link to the essay.
In that essay you will see approving definitions for time and space that are strictly matter related. Matt, in your last reply to my points, in the last few sentences, you said that you don’t care–as if you are neutral to whether the concepts of time and space are matter related–that you just care about getting the equations and concepts right. Yet, your last sentence is revealing of a position favoring that space and time have nothing to do with matter and motion, as if, perhaps, that the concepts of space and time have an independent existence.
Regarding that last paragraph I will explain gravity waves as a product of matter in motion a number of paragraphs below.
I did read your link about matter and energy in your previous post to me and believe that it is good that you wrote about this. I disagree with some of it. In my conception, which I shall try to justify to you and your colleagues, energy is the active mode of matter….
On the page that you requested that we should see, you wrote:
—————-
Matt Strassler | April 12, 2012 at 2:52 PM | Reply
“Photons are “stuff”, but they are not matter — for almost every definition of “matter”. Matter is a subset of stuff, though which subset depends on context. I do know of one or two contexts where photons would be called “matter” too — but these settings are ones that you won’t come across often, and usually different terminology is used anyway.
What I mean by “stuff”, in general, needs a little more working out. A silly but useful working definition is that something is stuff if it can be used to damage other stuff. I can’t damage your cells with mass or energy — I can’t make an “energy beam” or something like that. I have to make a beam of photons or a beam of electrons or muons or protons or neutrinos. That “stuff” carries energy, sure, but the energy has to be carried by a physical object — a particle — stuff — for it to be able to do anything.
(The particles of dark matter — whatever they turn out to be — are stuff too, though I’d need one heck of a beam of dark matter particles to damage anything!)
Fields are stuff too: they can be used to pull other stuff apart.
Maybe you can point out a flaw in that definition? A challenge to the reader…”
—————
That was fine with the exception saying that photon stuff is not matter. And previously you wrote:
—————
“Photons should not be called ‘energy’, or ‘pure energy’, or anything similar. All particles are ripples in fields and have energy; photons are not special in this regard. Photons are *stuff*; energy is not.”
“The stuff of the universe is all made from fields (the basic ingredients of the universe) and their particles. At least this is the post 1973 viewpoint.”
—————
From what I have seen so far, the post 1973 viewpoint is vague and mysterious. In my opinion Erwin Schrödinger got it right when he wrote:
“Today a physicist no longer can distinguish significantly between matter and something else. We no longer contrast matter with forces or fields of force as different entities; we know now that these concepts must be merged. It is true that we speak of “empty” space (that is, space free of matter), but space is never really empty, because even in the remotest voids of the universe there is always starlight—and *that* is matter.” From “What Is Matter?” Scientific American, September 1953.
I say vague and mysterious because many physicists talk about fields as if they are not composed of matter, as if they are composed of points with mathematical values instead of particles of matter having inertia. Perhaps the vectors and tensors are just place holders for what matter is doing, but that is hard to tell from what I have seen. As an example of my frustration with today’s physics let’s look at two paragraphs from Chapter 3, page 38 of Lee Smolin’s “The Trouble With Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next.”:
“From Newton to Einstein, a single idea dominated: *The world is made of nothing but matter.* Even electricity and magnetism were aspects of matter–just stresses in the aether. But this beautiful picture was crushed when special relativity triumphed, for if the whole notion of being at rest or in motion is meaningless, the aether must be a fiction.”
“The quest for unification had to go somewhere, and there was really only one place to go. This was to reverse the aether theory: If fields are not made from matter, perhaps *fields* are the fundamental stuff. *Matter must then be made from fields.* ….”
While I don’t know where this conclusion of rest or motion being *meaningless* comes from (It isn’t my view of special relativity.) and why that should lead to the conclusion that fields aren’t made of matter, I still must ask what are fields made of? (Maybe that bad conclusion was developed back when so much of the physics community was still under the mistaken opinion of relativistic mass?)
To my conception fields are composed of material particles that have inertia. Waves are the part of those fields that represent relative compression and rarefaction of the particles in the fields. Quanta are the pulses (ripples) of higher or lower density represented by the waves of compression and rarefaction.
You query me to define matter. For the benefit of readers here who haven’t yet seen our conversation at your page: “At a Workshop; and Higgs Papers Are Out.” I accept this definition for matter:
Matter is that which occupies space and has inertia. Matters mode of existence is motion. Inertia and energy are two aspects to the same existence, other names for matter and motion. They are forever and always linked. Empty space, or more correctly, emptier space, is necessary for motion to occur. Existence requires these types of dualalities.
About Space and Time:
It is essential to know that in the evolution of concepts, the word space first of all applies to matter in the sense of that which extends spatially. L. Feuerbach makes an interesting and succinct statement about space and time in an argument against the philosophical idealism of Hegel:
“In reality, exactly the opposite holds good, …it is not things that presuppose space and time, but space and time that presupposes things, for space or extension presupposes something that extends, and time, movement, for time is indeed only a concept derived from movement, presupposes something that moves. Everything is spatial and temporal….”
–Lenin, V. I., “Philosophical Notebooks,” Collected Works, Vol. 38, p. 70 (Moscow, 1981).
From the above preferred definitions we should be able to come to an explanation for gravity/space-time curvature as that due to the presence of lopsided distributions of bound-up matter/energy relative to freed-up matter/energy.
As we keep in mind that atoms are mostly empty and that the ratio of photons to protons is more than one billion to one. If then we also treat all motion as changes of place of an entity having mass and give photons the mass that they logically ought to have, it then should follow that bound-up matter/energy is less energy rich (active in the way that field interactions matter) than the surrounding field of interactions. This would cause a motion of all things toward the less active matter/energy bound-up stuff. Your page describing atomic arrangements as possessing less energy I found to be very welcoming as it seems to fit my conception here.
In my conception, gravity waves are the result of field matter particles filling in the regions where large masses have recently been. As the field particles move to a new equilibrium as large bodies move they create in their wake momentary rarefaction in the field. This is analogous to a suction in air or water. (Stay away from a large fast moving ship as it will suck you in following its wake.) This causes ripples of extremely low wavelength to pass through the field.
Now that I have offered a possible materialistic explanation for gravity waves, it is, I hope, a small jump to account for gravity which has traditionally been explained as due to space-time curvature; which itself is caused by mass or the transformation of space-time coordinates (non free fall acceleration) within a frame of reference.
In conclusion, it is not at all clear, as you wrote, that “there can be waves (and even black holes) even within a theory of only space and time, with nothing else like photons or electrons or other fields of any sort.”
I say we need the high energy matter fields to account for all the actions that have been referred to as the four forces.
I regard you as a parody on me. Also I was thinking I am a harmless one. I must be careful.
Matt, I understand your reluctance to jump straight to operators and eigenvalues in Hilbert space, Fock space, and the “second quantization”, but I do think it needs to be said that you have just started to scratch the surface of how things actually seem to work quantum mechanically, and how non-intuitive they really are. People from Einstein to Bell to Bohm to ‘t Hooft and Smolin and many more have struggled with the apparent inconsistencies that pop up with and within QM — and not just because they didn’t “like” QM. [QM and General Relativity are fundamentally incompatible at their core, and Einstein recognized this. Of course, he “preferred” GR, not QM, but for fundamental reasons concerning the nature of causality, of the apparent dynamics of space and (especially) of time, and for mathematical reasons such as the requirement for general covariance. The basic mathematics of a quantum mechanical state as described by Dirac and von Neumann et al have inconsistencies built into them that still haven’t been fully resolved.] Your description of the nature of knowledge is deeply profound – not just “scientific knowledge” but what we as humans can ever be able to actually “know” (as opposed to guess at, conjecture about or to assume). We tend to think of things like “particles” and “vibrations” as they relate to the things we commonly feel and touch and see, but much of QM just doesn’t behave that way. The very idea that something that we call a “particle” cannot have both a position and a momentum at the same time seems ludicrous to us, but it is how the world appears to work. This apparently isn’t the Heisenberg “uncertainty principle” of measurement affecting what we try to measure, but an actual property of time, space, and energy. [E.g., you can show that a spin 1/2 “particle”, which could be an electron or even an entire atom, didn’t travel over path 1, or over path 2, or any other path; but it got from point A to point B and deposited momentum!] It becomes what logicians call a “category error” to even ask the two questions simultaneously — sort of like “What color is that sound?” Although we can use the same mathematical formulas that we developed and derived for the macroscopic world we perceive to describe (with some difficulty) quantum mechanical effects, that does not mean that we can transfer our human-scale understanding directly to QM. As you say, at this point, all we can do is accurately record what our instruments tell us about the universe that we cannot directly or reliably perceive, and try to come up with ways of predicting and post-dicting those observations. And so far, the only reliable way of doing that is through increasingly complex, subtle mathematics. I don’t mean to sound like the old-school “Copenhagen interpretation” approach of Bohr and Heisenberg about the quantum realm being “unknowable” — just that it is apparently nothing like what we would expect given our human-scale perceptions and our human intellects that evolved to handle those perceptions. So good luck in the quest to make what we do know “understandable” to those of us without that deep math background. Because it probably won’t “make sense” in the normal sense of those words. It will just be the way things actually are.
In fact, non-commuting operators are themselves a clear indication of the fuzziness of action: all non-commuting operators indicate that those pairs of physical magnitudes (that present non-commuting operators) cannot be precisely measured at the same time, because the eigen-value of either one of the operators is not at the same time an eigen-value of the other operator of the pair, so, there is a uncertainty in the determination of both magnitudes at the same time.
But for each operator alone of the a given pair (of non-commuting operators), the eigen-value can be precisely determined, so, there is no uncertainty involved in the measurement of an individual magnitude of any of the pairs that form non-commuting operators.
Remember this article is intended for people who’ve had a bit of first-year physics; operators and eigenvalues and wave functions all come later. I’d rather not clutter the comment section with things that many readers won’t understand… there are lots of good websites about quantum mechanics for those who once had a class on the subject.
Regarding the principle of action, in classical physics, action has a crisp and precise value for any given system, but action in quantum physics becomes fuzzy.
As Prof. Strassler says, it is very technical to include the principle of action as a way to explain these topics in a forum like this, even though action shows up on many important parts of this discussion, like in the Uncertainty Principle: all pairs of physical magnitudes that present non commuting operators belong to action (a scalar) expressions, like the inner product of the variation of linear momentum (a vector) with the variation of position (a vector), or the product of the variation of energy (a scalar) and the variation of time (a scalar).
Beyond the 1920s’ forms of quantum physics, the path integral formulation is clear theoretical proof of the fuzziness of action in quantum physics.
The fuzziness of action in quantum physics appears also in many experiments, like the experiment of interference of a single electron passing through a double slit.
So, we know both from experiments and from theory, that action becomes fuzzy in quantum physics.
I just realized that I made a mistake: eigen-values come in discrete sets of values (in the sense that they cannot represent a continuous function), but for certain differential equations (like Schrodinger’s equation) that set could have infinite terms, so, they are not necessarily a small set.
Kind regards, Gastón
Professor Strassler,
In your exercising of the dialectic with me, on this point, I believe you have stepped back too far in your look at the issues. The points you have brought up are not as magnified to the smallest scale as what I am referring to. (And before there can be a concept, an abstraction, a number, a measurement, or an idea about something there must be something behind these things that is material.)
The determination of position entails a larger scale that includes spatial and temporal grids, and as position and momentum of a thing are conjugate variables an exact determination of position, while not forthcoming, does not mean, in my opinion, that a foundational entity is not a separate quantized thing since the very act of measuring such a tiny thing means interacting with it and that interaction thereby imparts a changed momentum and thereby, of course, changing its position. So while it is true what you say about position of particles not being quantized, I suggest this is due to the larger scale that one must work with in practice to *measure* position, and the fact that mere measurement leads to indeterminacy of position or momentum at the quantum scale.
Frequency, mass and energy are also concepts that, in my opinion, also fall into the categories of being at a scale that is larger than the fundamental scale that I’m suggesting. The act of measuring these things naturally leads to quantum indeterminacy which can hide the essential elements of existence–that there needs to be “thing” and “nothing” and “thing” needing to be separable from other “things.”
I hope this helps at reducing the vagueness you referred to.
In a few ways it helps, but in others it doesn’t. You say that “Frequency, mass and energy are also concepts that, in my opinion, also fall into the categories of being at a scale that is larger than the fundamental scale that I’m suggesting.” How do you intend to measure or define “scale” without these quantities available? What quantities *are* available for us to measure and discuss?
Your notion of “thing” remains extremely unclear to me, though I suppose you have a definition that you prefer. Could you please define what a “thing” is? What properties does a “thing” have that makes it distinct from “nothing”?
We, as complicated conscious creatures of a material universe, love to define everything with a level of complexity that suits our needs as complicated beings. I think we have to ask ourselves if nature at the most fundamental, most essential, level really needs to be so complicated in its essential being. There are plenty of examples in the universe of very simple actions of matter in motion ultimately leading to very complex patterns of organization and chemistry and ultimately in our case of self-organization (DNA, RNA) and consciousness. Previous to our animal existence there were no creatures that could ask about mass, frequency or scale, yet the world, while simpler, (because it didn’t contain anything as complicated as us) back then existed all the same. My point is I don’t think we need to define scale or even measure anything, assuming we can, at the fundamental level of existence. All that is needed is to understand the dialectics of the situation.
As far as defining “thing” I believe “thing” to be matter, but I was wanting to avoid calling it that for the time being because the concept of matter for a lot of people comes with a lot of uncertainty as to what must be its essential characteristics. We got into this subject more extensively on your page “At a Workshop and Higgs Papers Are Out” at
http://profmattstrassler.com/2012/08/02/at-a-workshop-and-higgs-papers-are-out/#more-4139
and I would just be repeating my points if I got further into it here.
I still have not seen from that previous chain of discussion a satisfactory reply to my point that there cannot be motion without matter. Therefore, I’m trying another approach here while also advocating for matters essential quantum and discrete nature.
We are talking badly at cross-purposes. One of the lessons that I take from the first half of the 20th century is completely opposite to the one you take. Every attempt to make sense of the world that has not involved a very precise definition of how physical quantities are to be measured has led nowhere; I speak specifically of Einstein’s very careful use of clocks and rods to define sets of observers relative to which measurements become meaningful; of Heisenberg’s and others’ careful definition of observables, as opposed to things that can be written down on paper but not measured in experiments; of observables in quantum field theory, which, if improperly defined, are mostly infinite or zero (on paper). In my courses, teaching graduate students, and commonly in my own research, I repeatedly emphasize the need for precise definitions of physical properties; if you make the wrong definitions and ask the wrong questions, your equations will tell you physically non-sensical things.
So I hear your nice words, and I think: does this man have any experience with actual equations? Has he seen how badly things can go wrong when we calculate things that sound nice but don’t, on careful examination, make sense?
“can there be motion without matter”? Define “matter”. First of all, there’s a semantic issue. The word “matter” as used by modern physicists is ambiguous (see http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/matter-and-energy-a-false-dichotomy/ , where I discussed this at length) and I am pretty sure that the way you are using the term is different from the way modern physicists use it. So I can’t answer your question without a precise definition of “matter”. Second, define “motion”. According to Einstein (and data from stars that orbit each other closely), there are gravitational waves. These are changes in the relative distances between points in space. They carry energy and momentum from place to place. They move through what physicists would call the “vacuum” (i.e. matterless regions) of space. Now, is this motion or not? And are gravitational waves matter or not? The physicists I know would all say: this is motion (waves are moving from one place to another, carrying energy) and yet gravitational waves are not matter (they are part of space and time themselves.) But of course if you define space and time as being matter, then, by disagreeing definitions, we’d have disagreeing conclusions.
I don’t really care, honestly. I care about getting the equations and concepts right; if we’re debating definitions then we’re not debating substance. What is clear is that there can be waves (and even black holes) even within a theory of only space and time, with nothing else like photons or electrons or other fields of any sort.
Professor Strassler,
Thanks for the wonderful and wise commentary and replies.
Please pardon one small difference of opinion that I hope will be welcomed. You wrote:
“And of course the fact that the world is quantum in nature is completely invisible to our senses, and seems deeply problematic to our brains.”
As to why nature at the smallest scales is quantized we should be concerned if that *wasn’t* the case.
It seems to me that a good ontology and epistemology for existence requires that something (or being as it has been called) and nothing (or nonbeing or empty space) are foundations. That something, obviously, must be different from nothing. That something should have the characteristic of being separate from other somethings. If that weren’t true then that something wouldn’t be any different than nothing. Therefore, first principle: separateness.
Nothing is continuous — in that the space between somethings can be divided up any way one might choose.
Something is not continuous, it is discreet, therefore quantized. Can we all agree with the above?
I feel this is too vague, Vincent. It is not true that “nature at the smallest scales” is quantized. Some things are quantized, some are not. Position of particles, for example, is not quantized. Frequency is not always quantized. Mass is not quantized. Energy of a particle moving freely in space is not quantized. Space is not, as far as we know, quantized in the sense of being made from little boxes, like a lattice. [In fact if it were like a lattice it would be inconsistent with relativity.]
So the statement “Nothing is continuous” is ambiguous. We have no evidence that it is correct, but it depends on what you define by “thing”. So I certainly can’t agree with it as stated, because I don’t think you’ve yet defined your terms; nor is it clear to me that there is any set of terms for which the statement would be accurate.
Said better, perhaps: the statement “everything behaves quantum mechanically” is not equivalent to the statement “all quantities are discrete”.
Professor, about lattice vs. continuous spacetime: Could one measure such divergent results with (nearly) present technology?
Why is a lattice spacetime inconsistent with relativity? From what I’ve read, Causal Dynamical Triangulation has some discrete lenghts and is consistent (or closely) with relativity. Or is it?
My fault: I was careless. I should have written “regular lattice”.
Matt, thank you again for this wonderful resource to pester you with questions! In anticipation of your upcoming particle/fields topic:
If relativity tells us that light’s speed in a vacuum is nature’s absolute speed limit b/c of the speed’s effect on time and distance, are there specific implications there for the relationship between relativity and quantum physics if we can look at a photon as a traveling disturbance in the electromagnetic field (quantum perspective)?
Looking forward to the next posts!
Thanks,
Jim
There certainly are implications — many of them. And quantum field theory encodes them. Stay tuned.
Professor, how could one apply the ZPE equation 1/2 hv of, e.g, the EM field in the vacuum? It expresses the energy density in natural units or what?
Thanks.
Stay tuned; that’s something we’ll return to eventually. This is where we start running into infinities that we have to interpret very carefully to get the physics right… to the extent that we can.
Professor,
Thanks for the best edu’l site in physics I am aware of, esp your addiing of some clarifying math which is rarely done. To make a speciffic comment, I think in your “red” text it would be more accurate to say that n is a non-negative integer, b/c math text books usually qualify numbers -1, -2, etc as integers as well.
Thanks again.
Yours, bob
No worries, earldcox!
I meant that as a joke, Tom. I forgot the smiley face.
Tom! That’s the last time I come to your defense!
Thank you Prof. Strassler for your answer to my “WHY” question. I meant to ask it in the sense that you answered it, as a matter of how the math works, not the philosophical “Why”. Not to say that philosophy isn’t fun, of course!
I would like to add two cents to the “Why?” question. I suspect that we have expectations that nature will satisfy some sense of order or beauty that we can experience. At least, that is what makes science exciting for me.
I would further guess that our expectations are, ultimately, based on our sensations. As we are educated, we learn the differences between sensations and reality more and more finely. But as humans I believe we have the bias towards what we can imagine sensationally.
I think one has to be very careful about notions of “order” and “beauty”. Early astronomers wanted the planets to travel in circles and would have found ellipses ugly. Einstein found the quantum theory very ugly, because of its probabilistic predictions. Feynman found quantum field theory very ugly because of renormalization, which was then viewed as sweeping infinities under the rug, instead of (as we now think of it) organizing the problem correctly. A sense of what is beautiful changes with more knowledge.
Moreover, nature is not obligated to be beautiful from a human perspective… especially not from the point of view of our senses. Human senses are extraordinarily limited; we only see a tiny fraction of the electromagnetic spectrum; our hearing is limited to a rather narrow range; all sorts of processes occur around us that we don’t have any way to perceive. How many of us are aware of the photosynthesis going on in the plants around us? Or of the great diversity of types of atoms? Or that the stars that we see in the sky are not nearly at roughly equal distances from earth? And of course the fact that the world is quantum in nature is completely invisible to our senses, and seems deeply problematic to our brains.
It seems to me that Nature’s deepest order and beauty may be completely hidden from human senses and cognition, which are needed to assure our survival on earth, and are not aimed at allowing us to gain insight into the universe. It is not even clear that we can understand Nature at that level. Try explaining baseball to a monkey; now try explaining how the universe works to a human.
Indeed it is the limitations of our senses that make scientific instruments so absolutely essential.
That’s interesting I never really considered that the weak anthropic principle is very much like a genetic algorithm (hence connecting physics and artificial intelligence).
Thanks, Matt, a nice answer.
But I thought that the multiverse approach posited that our universe is just one of many, many, many, many different universes each with, perhaps, their own laws of physics. The laws of physics for any given universe would apply across the entire universe (since they would have emerged from the singularity event). Thus only in those universes where the laws permit life, and only in those universes where life evolves into intelligent beings would those intelligent beings be able to ask “why?” Hence, a multiverse approach essentially works like a genetic algorithm, generating random populations of universes. Our objective function (the goodness of fit function) would be for those universes that support life. In many universes, perhaps, there is no quantum structure. No quanta, probably no laws of physics that would allow the creation of atoms, hence no life.
Now I realize this little discussion of mine is WAY off the central theme of your site. I just thought that Tom had an interesting question.
Well, in principle we can speculate about such things. But that’s not physics; that’s armchair discussion. We have to go deeper to see what the logical issues are.
Your notion of a multiverse is correct as far as “the laws of physics being different” in each region — but when you look at what people really talk about, different laws of nature implies that the different regions have different types of particles and forces and maybe different numbers of dimensions. Quantum mechanics, as we understand it, is more than a law of physics; it is the very underpinning of physical law. It goes to the heart of what it is to know, to measure, to engage with the physical world through empirical study.
I know of no examples of a **theory** of the multiverse — with real equations so that you can actually try to calculate what happens — that does not assume quantum mechanics throughout all regions. I do not think this is an accident. I do not see how one could construct ANY theory of the multiverse that would have quantum mechanics in some regions (including our own) and classical (i.e. strictly non-quantum) mechanics in another. It would pose huge logical and mathematical paradoxes that would probably be impossible to solve. Maybe if these regions were strictly unconnected from one another it might be possible; but the multiverse idea typically involves regions that are causally disconnected now but may have shared a past or might share a future… and thus, even though they have different laws as you and I would observe them in daily life and in particle physics experiments and in cosmological studies, the different regions are still governed by one overarching equation: that of an underlying quantum mechanical theory.
Is there an anthropic reason for the Planck scale to be roughly as far from every day physics (or the electroweak scale) as it is? Having the scale where you see quantum effects be far lower than it is in our world should make it irrelevant and possibly indistinguishable from a non-quantum world, right? I can imagine that a world with all physics near the Planck scale would make intelligent life impossible, but couldn’t you have a theory that looks classical because the Planck scale is so far away you wouldn’t know about it?
You’re confused, I think. The “Planck scale” is a scale involving gravity and quantum mechanics COMBINED. That’s not to be confused with “Planck’s constant” h, which only has to do with quantum mechanics, and not with gravity. You could take the Planck scale to infinity; that would still leave atoms just as quantum as they are in our universe.
So I think you just made a semantic error here, and meant “Planck’s constant” and not the “Planck scale”, yes?
Even so, I think the answer to your questions is no. Our world is a great example of showing why the macroscopic is not easily protected from the microscopic; we may not be aware of how quantum mechanics affects us, but it most certainly does; the basic building blocks of atomic nuclei and atoms determine the possibilities for much larger structures, such as DNA; and photons don’t form structure but still impact our daily world. Moreover, macroscopic quantum effects are possible (superconductivity for instance, and lasers.) So it should be possible in any world that is quantum for a scientists in that world to eventually figure out that the classical picture is wrong. The classical picture is certainly incomplete; quantum mechanics helped resolve some paradoxes inherent in classical physics. As for whether observers can exist that are more affected by quantum mechanics than we are, I see no reason why not. We *are* quantum mechanical observers, in the end.
TBH, I didn’t realize the scale of Planck’s constant was unrelated to the Planck scale…
Thanks for the interesting reply. I’ll have to google “paradoxes in classical physics” and see where that leads me.
I know you’re a pretty educated reader — maybe this is a confusion that is widely shared and that I should address in a post or article. The language is somewhat unfortunate and inherently confusing.
Planck introduced his constant h when quantum mechanics first arose in the context of Black Body radiation; Einstein then followed by identifying light as coming in packets (“quanta”) with energy hν, where ν is the frequency of the light. The units of h are those of angular momentum; quantum mechanics is important when, for instance, you are dealing with something whose angular momentum is of order h, or whose mass times velocity times radius is of order h. For instance, the size of a hydrogen atom is not set by h alone; it is set by r ~ h / (m c α), where m is the mass of the electron, c is the speed of light, and α is the strength of electromagnetism (about 1/137) — the velocity of an electron in a hydrogen atom is about c α, independent of the mass of the electron. In short, if electrons became lighter, atoms would become larger, even with h fixed. Or if you make an atom out of a muon and a proton, that atom will be much smaller than hydrogen; a heavier object under similar forces has its quantum effects at shorter distances. So h does not fix a distance scale. Only if you tell me which particles you are making an atom out of, and what their properties are, is the quantum scale for that atom — and thus its typical radius — determined. This point is not limited to atoms; it is general.
Once you have gravity, however, and therefore Newton’s constant G, you can define a length scale: the Planck length L = ( h G / c3 )1/2 . [The definition is ambiguous up to factors of 2π ; let’s ignore this for now.] This length is independent of the properties of any of the particles of nature; it just depends on the speed of light, the strength of gravity, and Planck’s constant. You can similarly define a Planck Mass, which is M = ( h c / G )1/2; again this is a mass scale that doesn’t care about the properties of any of the particles of nature. The significance of these scales is that if you take an amount of mass that is about M and squeeze it down in size, you’ll form a black hole, and the radius of the black hole will about L. You can’t make sense of a black hole that is smaller than L (it will be highly quantum mechanical) and you can’t make a black hole from an amount of mass that is less than M. These statements again do not depend at all on the specific properties of any of the particles of nature.
Unfortunately (I tried) it mostly leads to garbage websites. There are so many.
One example I had in mind involves the proper treatment of a charged particle and its own radiation field; this is discussed in one of the last chapters of Jackson’s textbook “Classical Electrodynamics” and involves things like the Abraham-Lorentz model of the electron and the so-called “classical radius of the electron” (which turns out not really to be a physical quantity, because classical physics breaks down before you reach that distance scale.) Unfortunately I don’t know a particularly non-technical discussion.
Another example is that black-body radiation has a so-called “ultraviolet catastrophe” in classical physics; and resolving this puzzle helped lead physicists along a path which led to Planck’s quantum hypothesis.
Some of this is discussed in Pais’s book on Einstein, but that book assumes you know a lot of physics.
Thanks again. I’m not sure the Planck scale / Planck’s constant confusion would be common; in hindsight it should have been obvious to me the two are unrelated. The fact that there’s no real fixed distance (or energy) scale where things “become quantum” might be worth a post if you come up with a simple approach to explaining how different quantities scale.
Agreed. Thanks for the suggestion.
… and I know there is a multiverse solution to the question “why?” but then we have to ask ourselves a whole bunch of question about the nature of entanglement, the “real” nature of the quantum wave function, and, ultimately, why is there a multiverse mechanism. I don’t believe that even a TOE will obviate the need to ask why.
We have no idea WHY things are quantized. Moreover, if things weren’t quantized, we would have no idea why that was true either. Always what we learn in physics are answers that themselves pose new questions; I’m sure that if I had a good answer for you about why things are quantized, it would simply raise for you another “why” question. Face it: neither we nor our descendants will ultimately answer all the WHY questions, at least not based on scientific research alone. The only hope is that the questions become fewer, and simpler to state. No guarantees that will happen.
By the way, the multiverse would give no insights into this; the whole idea of the multiverse [if it exists — remember there’s no experimental evidence for this] is predicated on quantum mechanics, and it’s not as though [if those ideas are right] there are some parts of the universe where there’s no quantization. String theory, for instance, takes quantum mechanics as an assumption; if string theory it turned out to be a correct theory of the universe, it could not resolve the issue of why there is quantization at all, because it takes that as an assumption.
The power of science is not its ability to answer ultimate WHY questions. The power lies in its ability to provide predictive equations and insights into how nature works, based on a combination of empirical observation and theoretical reasoning. WHY nature works that way — WHY those are the right equations — you will not be able to answer, except by finding new and more profound predictive equations that explain the original ones; but about the new equations you will again be able to ask: “WHY are those the right equations?” There’s no end to this process.
We laugh as adults when we see a 3 year old ask “Why is A true?” and when told “Because B” asks “Why is B true?”, on to infinite regress until the parent simply says “Because.” Our current conversation is deeper and the questions are better and more thoughtful than any 3 year old can manage — and there’s no parent to end the discussion — but in the end, the logic of the conversation is the same.
Note that when a 3 year old asks “Why is A true?”, what they are actually asking is “How do you know that A is true ?”. They want to know how you can tell it is so, not why it is so. All adults should answer the question accordingly. If you do so, you do not get the cascading “Why” questions of the increasingly frustrated 3 year old, leading to an increasing flustered adult. (I know it’s not about quantum physics, but I think that everybody should know this).
In this spirit perhaps an historical response would be adequate ? Along the lines of : starting more or less with Newton, physicists built a view of the world where physical quantities can take on any value, have a well defined value at all times, can be measured with arbitrary precision (in principle), etc. It was a mechanistic view and philosophically suspect at first, but this worked so well for a while that it became accepted and the weirdness was mostly forgotten. But over time, with the study of electromagnetism in particular, phenomena started to appear that couldn’t be explained well this way, and hints of a fundamental discreteness in nature appeared. So physicists started trying stuff like “Well, let’s assume this discreteness is real. Let’s posit that the energy levels of this system can only take discrete values. What then ? And with clever analysis they started getting answers that worked. Up to the point that a full blown theory emerged, one were all three assumptions above are unqualifiedly false.
The problem with this is it’s no clear to me what examples could be used. Perhaps the hydrogen spectrum ?
Anyway, sorry for the long digression, I just found your website and I think it’s a gem. Your pages about the Higgs or QFT make it all seem so clear and natural, quite a feat for such subjects. So thanks !
I’m new to this blog … very appreciated. B. Jackson’s comment seems important. I notice in this blog M. Strassler often pointing out science follows where observation leads and is an effort to “explain” reality largely in a pragmatic sense of being able to pre and post dict observation and how nature works. This can seem inadequate to those with a habit or desire for “ultimate” answers to the Why question, but seems perfectly adequate and satisfactory to those who view the Why question as more of a “How” question and a request for evidence and process. If this latter became more often the expectation for the Why question then science would make more sense to lay people. And parents give better answers too. :{)
Always nice with a good lecture!
“the multiverse [if it exists — remember there’s no experimental evidence for this]”.
Isn’t there? I thought it was the only theory that correctly predicts the cosmological constant and perhaps the only one who predicts the cosmic coincidence observation? (That we live in a time when dark energy becomes noticeable, I believe.)
Isn’t that what the old Weinberg paper was about, and testing it would be the standard cosmology that seems to agree with the value. And if you believe it comes out of eternal inflation, it would be nice to have the Planck probe test that again.
What other experimental evidence would be needed? (Especially if none of the competitors can make similar predictions.)
Maybe a good answer to the question why quantization works can be given the following way. Classical physics takes a Lagrangian as a starting point and then imposes that the action associated with the Lagrangian be exactly minimized. This however does not always work as found in experiments. When one then just chooses to allow values that stay close to a minimized action one arrives at quantization. So correct me if i am wrong but following this logic the basic idea of quantum mechanics is minimization of the action is a good idea but sometimes nature is not close enough to this idea so we just look at everything close to the minimized action and punish behaviour that stays too far away from that minimized action.
Well… I am not sure this is a very helpful way to explain things to people who aren’t already very experienced with the principle of minimized action in classical physics. That won’t work here: the current set of articles is aimed at people who only had a few months of physics class. So this way of saying things is too technical on the one hand and too vague on the other. It’s really hard to find the right middle ground…
Just as Prof. Strassler clearly points out, factual sciences like Physics do not answer any questions on the “why” category.
But we could discuss some poignant arguments regarding the mathematical reasons that make us to determine that only a discrete set of values (that are also a function of certain integer numbers) can represent the values of physical magnitudes in elementary particles, or in any subatomic particle.
Any given function that is a solution to any specific form of Schrodinger’s equation is known in math as an eigen-function, or a characteristic function for that differential equation.
In all differential equations that have eigen-functions (including Schrodinger’s equation, but there are lots of other different differential equations with them! ), these functions never “show up” alone, as they always have some special companions called eigen-values, or characteristic values.
It could be proven that any given eigen-function of a certain differential equation can only have a small and discrete set of possible (valid) eigen-values.
So, now we have a solid and robust mathematical argument that, (as we already know that Schrodinger’s equation represents the complete known state of a system of subatomic particles, like say, an atom being the system), we know that the only possible mathematical solutions to that equation offer a discrete set of values for the physical magnitudes of the particles in that system (like say, the electron buzzing around the nucleus of a Hydrogen atom).
So, now we know that those specific magnitudes of the electron in that atom can only have those certain values, and now other possible values in between, because that’s what the eigen-values tell us.
So, we have a very solid, proven, and amply verified by lots of different experiments, argument behind the fact that physical magnitudes of subatomic particles are quantized as these magnitudes are the eigen-values of the eigen-functions that are the solutions for the differential equations that represent the state of such particles.
Perhaps what Tom is asking is _why_ the underlying phenomenology of the universe is quantized – I don’t think he meant that the quanta is an axiom of the theory used to make tings work out (like the original idea of Quarks [or Aces]). His question is rooted in the epistemology of natural laws. Why is the speed of light 2.997925 x 10^8 m/s and not something else – or why is there a speed of light? Why does the gravitational constant (G) have its value. If every experiment to date confirms the idea of the quanta, that is fine as far as the idea that the universe obeys the laws of quantum mechanics – but the more profound and more important question is Tom’s: WHY?
I have a foundational question: Does physics contain an answer for *why* everything is quantized? Or is that more of an axiom of the theory that we just have to accept?
No there’s no answer as to “why” things are quantized, but also I would not say that it is simply an axiom of theory; that puts theory ahead of experiment. It’s a “fact” of nature — which means that all experiments that have ever been done are consistent with it being true. More precisely: sets of experiments were done that posed many puzzles; equations were found that both post-dicted the results of previous experiments and pre-dicted, successfully, the results of many new ones; entire new technologies based on those equations were developed and no experiments contradicting those equations have been found. An axiom that underlies those equations is indeed that everything is quantized. But those axioms arose from trying to guess how to match the results of experiments. They’re not like math axioms; they are only acceptable because they match nature, and if someday a class of experiments is found whose results contradict them, they’ll be discarded in favor of something more profound.
Maybe the answer that TomM is looking for can be found in this article:
“Informational derivation of Quantum Theory”
http://arxiv.org/abs/1011.6451
There are also a few other similar articles, just google for “Informational derivation of Quantum Theory”.
So this means that the quantization is just necessary to satisfy some common sense assumptions about the world (called axioms), for example casuality.
(and also other axioms: perfect distinguishability, ideal compression, local distinguishability, and pure conditioning)
If anyone would be willing to explain how they arrived at such a proof, I wouldn’t mind… starting from the explanation what these axioms mean.
This is bugging me for quite some time now (since they published the article), unfortunately I am in no way able to deal with the mathematics they use in the article.
Well, I wouldn’t get too excited about this paper.
In any case I found two articles that explain this a little better:
http://www.sciencenews.org/view/generic/id/332557/title/Quantum_theory_gets_physical
http://physics.aps.org/articles/v4/55
Just as a note, your formatting for A = 1/(2 π) √ n h / ν M implies the root is under the 1 along with the 2pi, maybe should be A = 1/(2 π)*√ n h / ν M
thanks!
Dear professor Strassler, how the formula for A is obtained?
You need the methods that are taught in the first few weeks of a quantum mechanics course. Instead of Newton’s equations, you need either Schrodinger’s equation or (equivalently) Heisenberg’s matrix mechanics for the case of a linear restoring force (i.e. a quadratic potential energy.) Then you either solve a rather simple differential equation, or play around with infinite-size matrices in a clever way. Once you have the answer as to what the oscillation states are and their energies and wave functions, and you’ve learned to interpret them in terms of what they mean physically, you can try to interpret them specifically in terms of the amplitude of oscillation that they correspond to. And that gives you A — and moreover you can get a more precise answer than the formula I gave you. (My final formula for E is precise; everything else is a bit of a rough picture, enough to carry us through to particle physics.)
You could ask the same question about the little bit of atomic physics you learn in a beginning physics class. First you learn the Bohr model of the hydrogen atom. Then you learn it isn’t quite right and that actually there is an n quantum number and an l quantum number and there are other subtleties. How do you figure that out? You use the methods that you learn in the first few weeks of quantum mechanics: specifically, you carefully solve Schrodinger’s differential equation in the appropriate form for the 1/r^2 force.
So it’s out of the scope of this article, and out of my knowledge too 🙂 Thanks for the comments anyway
Yes – I’m afraid this simple answer has a complicated derivation. Actually it is rather simple in the end, once you know how to do it; but getting to that point… well, you’ll need more than this website for that.
Why does zero-point energy have to be this value: (1/2)h ν but not h ν or any other arbitrary value between 0 and 1 times h ν? where does this 1/2 come from? What is the reason that zero-point energy has to lie exactly in the middle between 0 and 1?
You have to do a simple but necessary calculation in quantum mechanics to find out the answer; it would be done within the first month of a quantum mechanics class. There are probably on-line resources to help you learn this; maybe one of my readers has a suggestion. I don’t intend to explain it; it’s a bit too technical.
Maybe the following will help sketch to you what is done to arrive at the (1/2)h ν: The harmonic quantum oscillator can be decribed by:
E\psi=[-(\hbar^2)/(2m)(d/dx)^2+(1/2)kx^2]\psi
What you do is try to find a psi that makes it possible for this equation to work(psi is a function). After some trial you will find that a*exp(-b*x^2) solves the equation(this is the ground state). Why does it solve the equation? On both sides of the equation you will be left with psi and some constant(if you plug in \psi=a*exp(-b*x^2) ) on the left hand side the constant is E on the right hand side some combination of b,k,m and hbar. What is left to do is read off the value of E by comparing left and right side that means read off what is written before the psi on the right side. IF you set b and k to the values ussually used in physics you will arrive at the (1/2)h ν that you find in the text.
Ah, o and 1 … what if, it is -1 and 1, then 0 could be the “zero-point energy”. Would that make Stephen Hawking happy? (Theory of Nothingness) 🙂
As far as I am concern we live in a “soap bubble”, one of many, and the energy that created our manifold “seeped in”, possibly with a big bang maybe not, from another manifold and/or the invisible universe, dark energy?
I am surprise to here that the zero=point energy is 1/2 because it is the same as saying energy can be quantized, and I wonder if this is valid? When you speak of quanta you are referring to an already created particle(s). Particles that were created from an analog variable, E, energy. So my question would be, and I would be echoing Feynman when he called it “hocus pocus” physics. How much of reality are we erasing, ignoring, when we use renormalization to go from the “real’ analog world to the convenient digital, quantum, math?
PS; What is energy?