1. Ball on a Spring (Classical)

© Matt Strassler [August 28, 2012]

This is article 1 in the sequence entitled Fields and Particles: with Math

If you want to understand particle physics, there’s basically one thing to remember from freshman physics, or even high school physics — and that’s how a spring works. Basically, anything that bounces, vibrates, rings, wiggles, rolls back and forth, or goes boing-boing-boing is, at heart, an example of a spring.

Let’s imagine we attach a ball to the end of a spring. The motion of a spring, and the equations behind that motion, are simple. What we’ll do is this: First, let’s recall the basic workings of a spring. Then we’ll look at the motion of the ball once it starts bouncing around — oscillation. And finally, for those who’d like to see it (it can be skipped for now if you want), we’ll review the equations that lead to that motion.

The Harmonic Oscillator (i.e. Ball on a Spring)

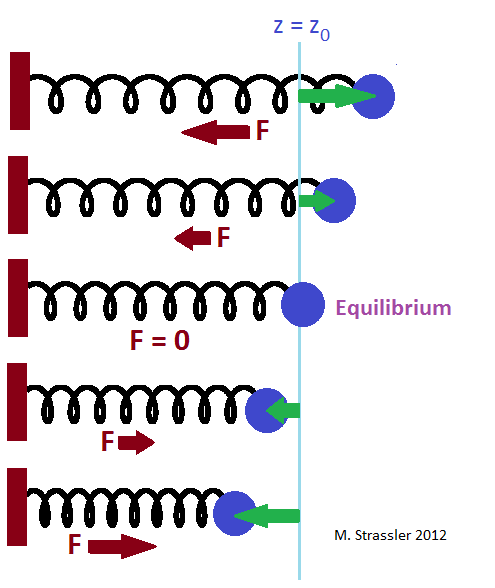
The ball on a spring has an equilibrium position; this is the location where if you place the ball there and let go of it, the spring will not push the ball in either direction, and the ball will remain stationary. This is the blue line in Figure 1. If you pull the ball away from its equilibrium position (green arrows in Figure 1), the spring will pull the ball back toward its equilibrium position with a force F (red arrow). The further you pull the ball, the harder the spring pulls back (at least as long as you don’t pull so hard that the spring breaks or becomes so compressed that it is crushed.)

Oscillatory Motion (i.e. Bouncing!)

Let’s call the direction in which the ball can move “the z direction”, and let’s define the z axis so that z=z₀ is the equilibrium position for the ball on the spring. Now suppose you pull the ball away from its equilibrium position, holding it so that it isn’t moving, at the position z = z₀ + A; and then, at a chosen moment in time (which we’ll call t=0) you let go.  The ball will start to bounce back and forth; see Figure 2.  The size of the bounce — the amplitude of the oscillation — is simply A.  It can be as big or small as you like; you chose how far to pull the ball away from equilibrium before you let it go.  But how often the back-and-forth bounce occurs — the frequency of oscillation ν — is not something you control.  It turns out to be the same no matter what A is; it is determined only by properties of the ball and of the spring, not by what you chose to do.  See Figure 2.

For scientific research it’s crucial to put these observations into a math formula.  The location z of the ball as a function of the time t, which we write as the function z(t), takes the form

• z(t) = z₀ + A cos [ 2 π ν t ]

where as usual cos is short for cosine, π is the number “pi” that shows up in circular geometry, z₀ is the ball’s equilibrium position, and A and ν (“nu”) are the amplitude and frequency of oscillation.  The cosine function is an oscillating function, so this formula represents oscillatory motion with amplitude A and frequency ν. Examples of oscillatory motion for a ball on a spring, with different values of the initial displacement (and resulting amplitude) A, are shown in Figure 2, which also illustrates that for a given ball and spring, the frequency ν doesn’t depend on the amplitude A.

Fine print: Both the amplitude and frequency are positive (or zero). If you chose A to be negative, then the amplitude is -A; in short the amplitude is really |A|, the absolute value of A.

What’s hugely important to remember about amplitude and frequency for the ball and spring (in classical [i.e.pre-quantum] physics.)

• You can choose whatever amplitude A you like;
• However, the spring and the ball determine ν, and the only way you can change the frequency ν is to replace the spring with a different one, or the ball with a different one.

The period of each oscillation (how long it takes for the ball to swing back and forth exactly once) we’ll call T, and the period is just the inverse of the frequency: T = 1/ν. If the period is 5 seconds, then the frequency is once-every-5-seconds, or 1/5 per second (often called 1/5 Hertz [Hz for short]).

More fine print: for any realistic ball-spring system you’ll encounter in daily life, friction will cause A to gradually become smaller, and eventually A will decrease to zero and the motion will stop. The formulas for the motion including the effects of friction aren’t that much more difficult to write down, but we won’t need them here.  So I’ll assume friction is always small, so that A decreases very slowly, and we can just use the simple formulas that ignore friction.  However, there’s one really important thing to know: friction decreases A, but (unless it is very strong) has no effect on ν, and on T!  The frequency of oscillation remains the same even as the amplitude decreases.  This is why the note produced by a guitar string after you pluck it does not change, even as the sound it produces becomes softer and dies away.

One more thing: there’s a nice formula for the energy stored in an oscillating spring.  It is proportional to the square of the amplitude and the square of the frequency:

• E = 2 π² ν² A² M

This energy is partly the ball’s motion-energy (“kinetic”) and partly relationship-energy (“potential”) stored in the spring, and as the ball swings back and forth, the partition of the total energy into these two types of energy changes back and forth.  But the total energy E is constant during the motion.  (Fine Print: There’s also the mass-energy of the ball, M c², but we’re not keeping track of that because that energy is present whether or not the spring is moving.)

This same oscillatory motion formula applies to pretty much everything that wiggles or bounces, as long as the wiggles aren’t too big: a ball rolling at the bottom of a bowl; a car bouncing on bad shock absorbers; a vibrating violin string or guitar string after it is plucked; a xylophone key after it is struck; and so on.

The Equation of Oscillatory Motion (i.e. Bouncing Math)

Now let’s remember the basic formulas that allow us to understand why the ball on the spring has oscillatory motion.  (You can skip this section at first reading; but at some point you may need it, especially if you want to understand how the Higgs field works.)

As we said at the beginning (Figure 1), the ball on the spring has an equilibrium position, which we can called z = z₀. Suppose that at any given moment (either because we’ve pulled on the ball, or because it is bouncing on its own) it is found at some other position z. Then if z > z₀, i.e. if the displacement from equilibrium z – z₀ is positive, then the spring will exert a force that is pointed in the negative z direction so as to pull the ball back toward the equilibrium point. Conversely, if z < z₀, i.e. if the displacement from equilibrium z – z₀ is negative, then the spring will exert a force that is pointed in the positive z direction, again so as to pull the ball back toward the equilibrium point. And the further the ball is away from the equilibrium position, the harder the spring pulls. The force F that the spring exerts is related to the displacement from equilibrium by

• F = – K (z – z₀)

where K is a positive quantity that depends on the specific spring, and is called the spring constant.

Note that this formula has the right properties:

• If the ball is at the equilibrium point, F = 0; the spring exerts no force, so if the ball is motionless at the equilibrium point, it will remain there (in equilibrium).
• If the displacement is positive, the force is negative.
• If the displacement is negative, the force is positive.
• The larger the displacement, the larger the force.

Next we appeal to Newton’s second law of motion, which tells us that under a force F, a ball of mass M will move with acceleration a, where F = M a. Plugging this into the previous formula gives us

• M a = – K (z – z₀)

or

• a = – K/M (z – z₀)

This is almost the equation we need to derive the oscillatory motion. We just need to remind ourselves about the relationship between a and z. To do that it is useful to remember the relationship between a and the velocity v, and between v and z. That relationship is one of change with time:

• the velocity is the change in time of the position, v = dz/dt
• the acceleration is the change in time of the velocity, a = dv/dt

[If you haven’t had calculus, the expression dz/dt looks strange; but it’s just a way of representing the words to the left of it, so focus on the words.] Putting these together

• a = d(dz/dt)/dt = d²z/dt²

the acceleration is the change in time of the change in time of the position.

We can then rewrite our formula as the equation of motion

• d²z/dt² = – K/M (z – z₀)        (*)

where z is shorthand for z(t). And now we can check that oscillatory motion z(t)= z₀ + A cos[ 2 π ν t ] is a solution to this equation of motion. All we need to do is first calculate the particle’s velocity as the change in time of its position:

• d/dt (z₀ + A cos[ 2 π ν t ]) = – (2 π ν) A sin[ 2 π ν t ]

(dz₀/dt = 0 since the equilibrium position z₀ isn’t changing with time, and d/dt(cos wt) = -w sin wt [the change in time of a cosine of a number w times t is equal to w times minus the sine of w times t]); and then we calculate the particle’s acceleration as the change in time of its velocity

• d/dt [– (2 π ν) A sin[ 2 π ν t ] ] = – (2 π ν)² A cos[ 2 π ν t ]

(because d/dt(sin wt) =  w cos wt [the change in time of a sine of a number w times t is w times the cosine of w times t].) Thus

• d²z/dt² = – (2 π ν)² A cos[ 2 π ν t ] = – (2 π ν)² (z – z₀)

where in the last step I used the formula z(t)= z₀ + A cos[ 2 π ν t ] for oscillatory motion.  This final equation is the same as our equation of motion [ d²z/dt² = – K/M (z – z₀)  ] provided that – (2 π ν)² = K/M, i.e., as long as the frequency of oscillation is

• ν = √ K/M   / 2π

So we have indeed found that our equation of motion implies the spring will oscillate with the above frequency, that this frequency does not depend on A — it depends only on properties of the spring (K) and the ball (M) — and that there is a solution to the equation no matter what A is.  Thus we are free to choose A to be any size, determined by however far we pull the ball away from the equilibrium point before we release it.

Next Up: The Quantum Ball on a Spring

That’s the ball on the spring in classical [i.e., pre-quantum] physics.  Quantum mechanics changes many things, but the most important is this: we are still free to choose A, but A cannot be of an arbitrary size.  Instead, it can only take special values, proportional to the square root of an integer.

Click here for the next article.