Resonance is one of the most important phenomena in nature, both in ordinary life (where it plays a role in many aspects of technology, and in music) and in the basic processes of the physical world, especially within particle physics. In this article I’ll briefly outline the basics of the concept.
Let’s first recall how a child’s swing works. A swing, like a ball on a spring, or a pendulum of any sort, is an oscillator — it “swings” back and forth with a definite frequency, and that frequency does not depend on the amplitude of the swing. [Fine point: for a pendulum or swing, that last statement is only true as long as the amplitude doesn’t become very large.] You probably know from experience that if you want to make the child swing higher, you should push the swing forward exactly once during each cycle, such as to always increase the amplitude of the swing. If you were to push the swing forward several times per cycle, or once every two and a half cycles, say, you’d end up sometimes increasing the amplitude of the swing and some times decreasing it. So clearly there’s something special about aligning the frequency with which you push the swing with the natural frequency of the swing itself.
Similarly, if the child knows how to swing higher on his or her own, he or she also knows how to swing his or her legs in time with the swing’s natural frequency, in order to get the amplitude of the swinging to increase. Swing any other way, and the amplitude won’t grow.
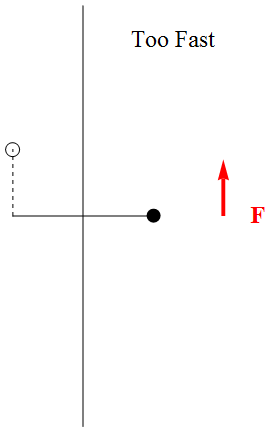
We can watch this happen with a ball on a spring, which I described in detail in a previous article. Take a look at the figure (click on t to animate it). On the left is shown a ball (open circle) oscillating back and forth around its equilibrium position. This ball is swinging back and forth on its own, without being pushed; it is oscillating with the natural frequency ν of the spring. [As explained here, this frequency is √ K/M , where K is the strength of the spring and M is the mass of the ball.]
But as you watch the animation, you’ll see on the right-hand side what happens to another ball (black, but with the same mass as the white ball, on an identical spring) being pushed with a force F (whose strength and direction are shown by the red arrow) whose direction and strength are oscillating with a frequency νF, which is generally different from ν. What happens to the black ball is similar to what would happen to a child’s swing if you pushed it too rarely; the swing would undergo a complicated motion and wouldn’t end up swinging very high. You can see in the figure animation that the ball doesn’t end up oscillating very smoothly and the amplitude of oscillation is small. If you look closely you can see the ball “trying” to oscillate with its natural frequency even though its overall motion is repeating with frequency νF .
Next the figure shows the case where the force is oscillating with a frequency νF which is much larger than the frequency ν. Again if you look closely you can see that the ball is trying to oscillate with its natural frequency, but it just can’t do so with a large amplitude, because the rapidly oscillating force is about as likely to push against the ball’s motion, decreasing the amplitude, as it is to increase it.
But finally the case is shown where the force oscillates with the natural frequency of the spring, νF = ν. The response of the ball is now dramatically different: the amplitude of the oscillation grows and grows, with the ball swinging back and forth as smoothly and easily as the white ball to its left, but with increasing amplitude. This is resonance.
In summary: If νF differs from ν — if the force drives the ball off-resonance — the ball will still move, but grudgingly, and its motion is very unlike its natural motion, of simple oscillations at the frequency ν. By contrast, if the force’s frequency is tuned to the natural frequency — if the force drives the ball on-resonance — the force is much more effective at pushing the ball, and the resulting motion is much more impressive. This is something we all know intuitively; it is by pushing with the natural frequency of the swing that a child (or a parent) assures the child swings high.
Among the very important aspects of resonance in particle physics is that, in certain circumstances, particles can be produced by a very similar mechanism: a force is obtained (through the collision of two particles) that has exactly the right frequency to make a third particle. To understand this remark you will first have to understand that particles are quanta (ripples in fields of minimal amplitude), which requires you finish my set of articles on Particles and Fields.


2 Responses
One time while in a California redwood forest I came across a giant redwood tree that had fallen over. There was about 50 or so feet of it that had no supports under it and was free to move, but moving that much tree with just my body strength alone wasn’t a real possibility, but I knew that I could introduce a resonance by grabbing a branch and slowly moving that branch to whatever that natural frequency that the free part of the tree had. Each time the tree sprung up a little I added a pull on the down motion. After doing this about 10 times I had that giant tree oscillating quite far, much farther than I could have moved it in any one single attempt. By leveraging a little bit of energy over multiple cycles on something with a natural frequency something was created ( a new level of motion and if applied to do work…) that wouldn’t have been there before.
Professor, I think this is what it is that you are talking about.