A few days ago I wrote a quick summary of a project that we just completed (and you may find it helpful to read that post first). In this project, we looked for new particles at the Large Hadron Collider (LHC) in a novel way, in two senses. Today I’m going to explain what we did, why we did it, and what was unconventional about our search strategy.
The first half of this post will be appropriate for any reader who has been following particle physics as a spectator sport, or in some similar vein. In the second half, I’ll add some comments for my expert colleagues that may be useful in understanding and appreciating some of our results. [If you just want to read the comments for experts, jump here.]
Why did we do this?
Motivation first. Why, as theorists, would we attempt to take on the role of our experimental colleagues — to try on our own to analyze the extremely complex and challenging data from the LHC? We’re by no means experts in data analysis, and we were very slow at it. And on top of that, we only had access to 1% of the data that CMS has collected. Isn’t it obvious that there is no chance whatsoever of finding something new with just 1% of the data, since the experimenters have had years to look through much larger data sets?
Not only isn’t it obvious, it’s false. In an immense data set, unexpected phenomena can hide, and if you ask the wrong questions, they may not reveal themselves. This has happened before, and it will happen again.
Conventional thinking, before the LHC and still today, is that new phenomena will likely appear in the form of particles with large rest masses. The logic? You can’t easily explain the patterns of particles in the Standard Model without adding some new, slightly heavier ones. Crudely speaking, this would lead you to look for particles with the largest rest masses you can reach, which is limited by the energy of your machine, because of E=mc². That’s why the LHC was expected to find more than just the Higgs particle, and why the machine proposed for the post-LHC era at CERN is a larger copy of the LHC, with more energy in each collision.
This point of view is based on strong, reasonable arguments; please don’t think I’m criticizing it as foolish. But there have long been cracks in those arguments. Studies of so-called “gauge-mediated” supersymmetry breaking in the mid 1990s, which revealed a vast world of previously ignored phenomena. The discovery of the cosmological constant in 1998, which clearly violated conventional reasoning. The possibilities of relatively large unobserved dimensions of space (which we, like blind flies stuck between panes of glass, can’t detect), which showed how little confidence we should have in what we think we know. The model known as the Twin Higgs in 2005, which showed how the new heavy particles might exist, but could hide from the LHC.
In this context, it should not have been a total shock — just a painful one — that so far the LHC has not found anything other than a Higgs boson, using conventional searches.
Indeed, the whole story of my 30-year career has been watching the conventional reasoning gradually break down. I cannot explain why some of my colleagues were so confident in it, but I hope their depression medication is working well. I myself view the evisceration of conventional wisdom as potentially very exciting, as well as very challenging.
And if you’re a bit unconventional, you might wonder whether particles that are insensitive to all the known forces (except gravity) might have an unexpected role to play in explaining the mysteries of particle physics. Importantly, these (and only these) types of particles could have arbitrarily low rest mass and yet have escaped discovery up to now.
This unconventional thinking has made some headway into the LHC community, and there have been quite a number of searches for these “hidden” particles. BUT… not nearly enough of them. The problem is that (a) such particles might be produced in any of a hundred different ways, and (b) they might disintegrate (“decay”) in any of a hundred different ways, meaning that there are many thousands of different ways they might show up in our experiments. Don’t quote me on the numbers here; they’re for effect. The point is that there’s a lot of work to do if we’re going to be sure that we did a thorough search for hidden particles. And one thing I can assure you: this work has not yet been done.
Fortunately, the number of searches required is a lot smaller than thousands… but still large: dozens, probably. The simplest one of them — one that even theorists could do, and barely qualifying as “unconventional” — is to look for a hidden particle that (1) decays sometimes to a muon/anti-muon pair, and (2) is initially produced with a hard kick… like shrapnel from an explosion. In colloquial terms, we might say that it’s faster than typical, perhaps very close to the speed of light. In Physicese, it has substantial momentum [and at the LHC we have to look for momentum perpendicular (“transverse”) to the proton beams.]
There’s an obvious way to look for fast hidden particles, and it requires only one simple step beyond the conventional. And if you take that step, you have a much better chance of success than if you take the conventional route… so much better than in some cases you might find something, even with 1% of the data, that nobody had yet noticed. And even if you find nothing, you might convince the experts that this is an excellent approach, worth applying on the big data sets.
So that’s why we did it. Now a few more details.
What we did
There’s nothing new about looking for new particles that sometimes decay to muon/anti-muon pairs; several particles have been discovered this way, including the Z boson and the Upsilon (a mini-atom made from a bottom quark/anti-quark pair.) It’s not even particularly unconventional to look for that pair to carry a lot of transverse momentum. But to use these as the only requirements in a search — this is a bit unconventional, and to my knowledge has not been done before.
Why add this unconventional element in the first place? Because, as Kathryn Zurek and I emphasized long ago, the best way to discover low-mass hidden particles is often to look for them in the decay of a heavier particle; it may be the most common way they are produced, and even if it isn’t, it’s often the most spectacular production mechanism, and thus the easiest to detect. Indeed, when a particle is produced in the decay of another, it often acts like shrapnel — it goes flying.
But it’s hard to detect such a particle (let’s call it “V”, because of the shape the muon and anti-muon make in the picture below) if it decays before it has moved appreciably from the location where it was created. In that case, your only clue of its existence is the shrapnel’s shrapnel: the muon and anti-muon that appear when the V itself decays. And by itself, that’s not enough information. Many of the proton-proton collisions at the LHC make a muon and anti-muon pair for a variety of random reasons. How, then, can one find evidence for the V, if its muon/anti-muon pair look just like other random processes that happen all the time?
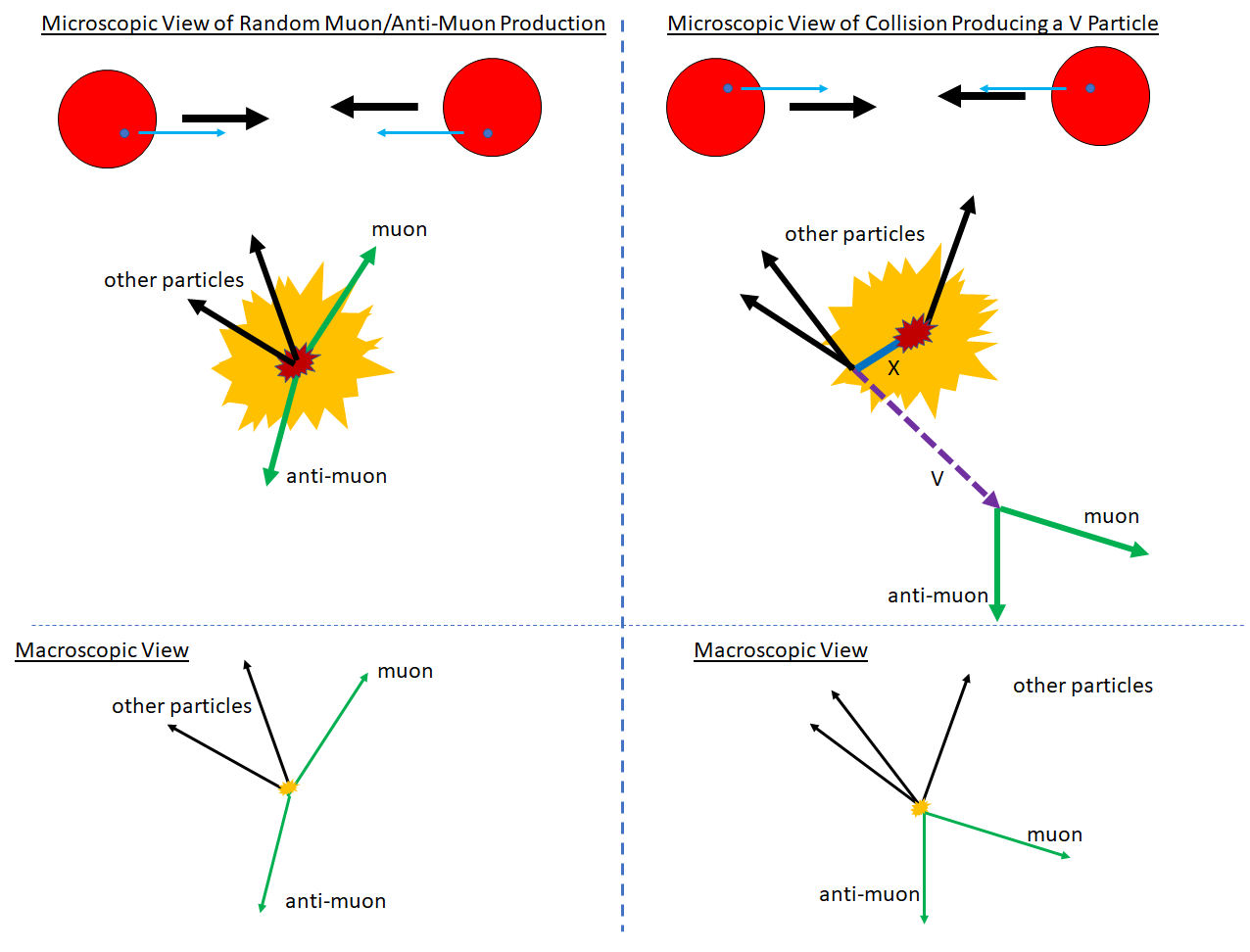
One key trick is that the new particle’s muon/anti-muon pair isn’t random: the energies and momenta of the muon and anti-muon always have a very special relationship, characteristic of the rest mass of the V particle. [Specifically: the “invariant mass” of the muon/anti-muon pair equals the V rest mass.] And so, we use the fact that this special relationship rarely holds for the random background, but it always holds for the signal. We don’t know the V mass, but we do know that the signal itself always reflects it.
The problem (both qualitatively and quantitatively) is much like trying to hear someone singing on your car radio while stuck in a deafening city traffic jam. As long as the note being sung is loud and clear enough, and the noise isn’t too insane, it’s possible.
But what if it’s not? Well, you might try some additional tricks. Noise reduction headphones, for example, would potentially cancel some of the traffic sound, making the song easier to hear. And that’s a vague analogy to what we are doing when we require the muon and anti-muon be from a fast particle. Most of the random processes that make muon/anti-muon pairs make a slow pair. [The individual muon and anti-muon move quickly, but together they look as though they came from something slow.] By removing those muon/anti-muon pairs that are slow, in this sense, we remove much of the random “background” while leaving much of the signal from any new particle of the sort we’re looking for.
Searches for particles like V have come mainly in two classes. Either (1) no noise-cancelling tricks are applied, and one just tries to cope with the full set of random muon/anti-muon pairs, or (2) a precise signal is sought in a highly targeted matter, and every trick one can think of is applied. Approach (1), extremely broad but shallow, has the advantage of being very simple, but the disadvantage that what you’re looking for might be lost in the noise. Approach (2), deep but narrow, has the advantage of being extremely powerful for the targeted signal, but the disadvantage that many other interesting signals are removed by one or another of the too-clever tricks. So if you use the approach (2), you may need a different search strategy for each target.
Our approach tries to maintain tremendous breadth while adding some more depth. And the reason this is possible is that the trick of requiring substantial momentum can reduce the size of the background “noise” by factors of 5, 25, 100 — depending on how much momentum one demands. These are big factors! [Which is important, because when you reduce background by 100, you usually only gain sensitivity to your signal by 10.] So imposing this sort of requirement can make it somewhat easier to find signals from fast hidden particles.
Using this approach, we were able to search for fast hidden short-lived particles and exclude them without exception across a wide range of masses and down to smaller production rates than anyone has in the past. The precise bounds still need to be worked out in particular cases, but it’s clear that while, as expected, we do less well than targeted searches for particular signals, we often do 2 to 10 times better than a conventional broad search. And that benefit of our method over the conventional approach should apply also to ATLAS and CMS when they search in their full data sets.
Some Additional Technical Remarks for our Experimental Colleagues:
Now, for my expert colleagues, some comments about our results and where one can take them next. I’ll reserve most of my thoughts on our use of open data, and why open data is valuable, for my next post… with one exception.
Isolation Or Not
Open data plays a central role in our analysis at the point where we drop the muon isolation criterion and replace it with something else. We considered two ways of reducing QCD background (muons from heavy quark decays and fake muons);
- the usual one, requiring the muons and anti-muons be isolated from other particles,
- dropping the isolation criterion on muons altogether, and replacing it with a cut on the promptness of the muon (i.e. on the impact parameter).
With real data to look at, we were able to establish that by tightening the promptness requirement alone, one can reduce QCD until it is comparable to the Drell-Yan background, with minimal loss of signal. And that means a price of no more than √2 in sensitivity. So if chasing a potential signal whose muons are isolated < 85% of the time (i.e. a dimuon isolation efficiency < 70%) one may be better off dropping the isolation criterion and replacing it with a promptness criterion. [Of course there’s a great deal of in-between, such as demanding one fully isolated lepton and imposing promptness and loose isolation on the other.]
It’s easy to think of reasonable signals where each muon is isolated less than 85% of the time; indeed, as Kathryn Zurek and I emphasized back in 2006, a feature of many relevant hidden sector models (“hidden valleys” or “dark sectors”, as they are often known) is that particles emerge in clusters, creating non-standard jets. So it is quite common, in such theories, that the isolation criterion should be dropped (see for example this study from 2007.)
Our Limits
Our main results are model-independent limits on the product of the cross-section for V production, the probability for V to decay to muons, and the acceptance and efficiency for the production of V. To apply our limits, these quantities must be computed within a particular signal model. We’ve been working so hard to iron out our results that we really haven’t had time yet to look carefully at their detailed implications. But there are a few things already worth noting.
We briefly compared our model-independent results to targeted analyses by ATLAS and CMS for a simple model: Higgs decaying to two pseudoscalars a, one of which decays to a bottom quark/anti-quark pair and one to a muon/anti-muon pair. (More generally we considered h→Va where V, decaying to muons, may have a different mass from a). If the V and a mass are both 40 GeV, our limits lag the targeted limits by a factor of 15-20. But the targeted limits used 10-20 times as much data as we had. One may then estimate that with identical data sets, the difference between our approach and theirs would likely be somewhere between 5 and 10.
Conversely, there are many models to which the targeted limits don’t apply; if a usually decays to gluons, or the a mass is so low that its decay products merge, we still set the same limit, while the published experimental analyses, which require two b-tagged jets, do not.
Thus broad analyses and deep analyses are complementary, and both are needed.
The wiggle at 29.5 GeV and what to do about it
In our limit plots, we have a few excesses, as one would expect with such a detailed mass scan. The only interesting excess (which is not the most significant) is found in a sample with no isolation criterion and a cut of 25 GeV on the dimuon pair — and what makes it interesting is that it is at 29.5 GeV (and locally 2.7σ) which is quite near to a couple of other curious excesses (from ALEPH data and by CMS) that we’ve heard about in the last couple of years. Probably it’s nothing, but just in case, let me say a few cautious words about it.
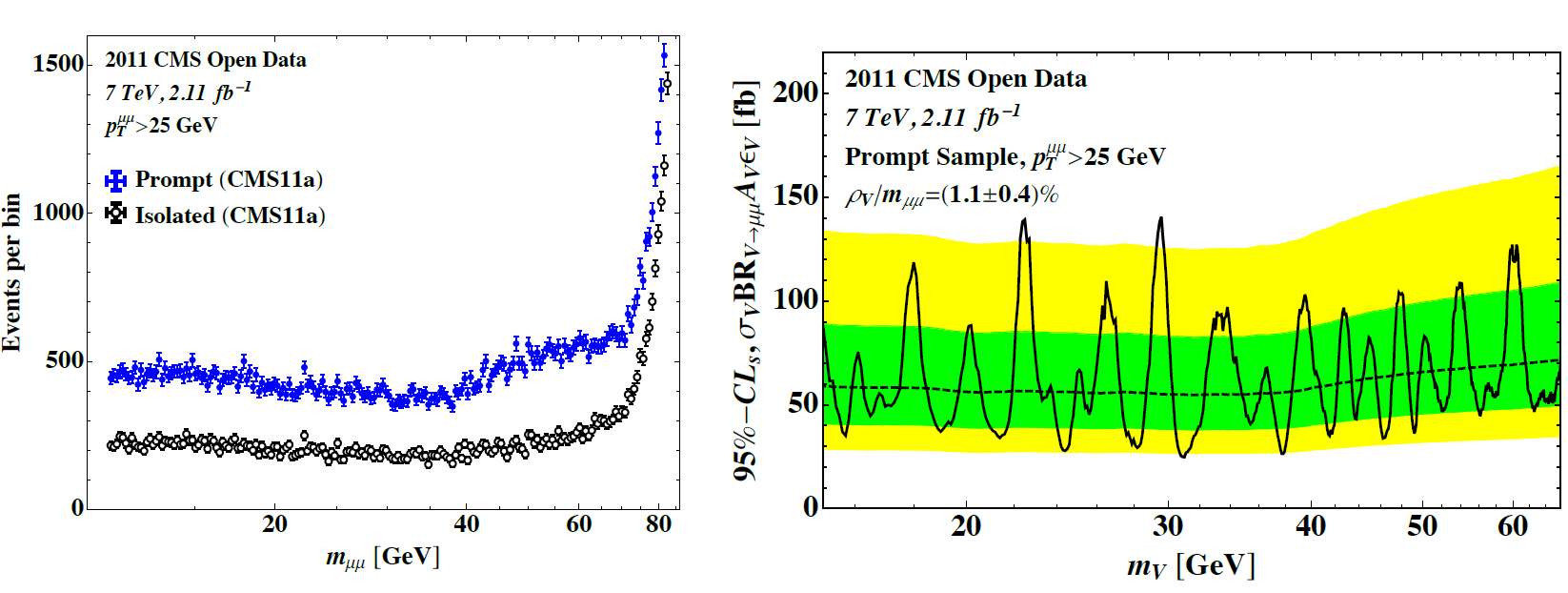
So let’s imagine there were a new particle (I’ll keep calling it V) with mass of about 29 GeV. What would we already know about it?
The excess we see at 29.5 GeV does not appear in the isolated sample, which overlaps the prompt sample but is half its size (see the figure above left), and it’s not visible with a transverse momentum cut of 60 GeV. That means it could only be consistent with a signal with transverse momentum in the 25-50 GeV range, and with often-non-isolated leptons.
If it is produced with bottom (b) quarks all of the time, then there’s no question that CMS’s studies, which require a b-tagged jet, are much more sensitive than we are, and there’s no chance, if they have only a ~3σ excess, that we would see any hint of it.
But if instead V is usually produced with no b quarks, then the CMS analysis could be missing most of the events. We, in our model-independent analysis, would miss far fewer. And in that context, it’s possible we would see a hint in our analysis at the same time CMS sees a hint in theirs, despite having much less data available.
Moreover, since the muons must often be non-isolated (and as mentioned above, there are many models where this happens naturally) other searches that require isolated leptons (e.g. multilepton searches) might have less sensitivity than one might initially assume.
Were this true, then applying our analysis [with little or no isolation requirement, and a promptness cut] to the full Run II data set would immediately reveal this particle. Both ATLAS or CMS would see it easily. So this is not a question we need to debate or discuss. There’s plenty of data; we just need to see the results of our methodology applied to it.
It would hardly be surprising if someone has looked already, in the past or present, by accident or by design. Nevertheless, there will be considerable interest in seeing a public result.
Looking Beyond This Analysis
First, a few obvious points:
- We only used muons, but one could add electrons; for a spin-one V, this would help.
- Our methods would also work for photon pairs (for which there’s more experience because of the Higgs, though not at low mass) as appropriate for spin-0 and spin-2 parent particles.
- Although we applied our approach below the Z peak and above the upsilon, there’s no reason not to extend it above or below. We refrained only because we had too little data above the Z peak to do proper fits, and below the Upsilon the muons were so collimated that our results would have been affected by the losses in the dimuon trigger efficiency.
More generally, the device of reducing backgrounds through a transverse momentum cut (or a transverse boost cut) is only one of several methods that are motivated by hidden sector models. As I have emphasized in many talks, for instance here, others include:
1) cutting on the number of jets [each additional jet reduces background by a factor of several, depending on the jet pt cut]. This works because Drell-Yan and even dileptonic top have few jets on average, and it works on QCD to a lesser extent. It is sensitive to models where the V is produced by a heavy particle (or particle pair) that typically produces many jets. Isolation is often reduced in this case, so a loose isolation criterion (or none) may be necessary. Of course one could also impose a cut on the number of b tags.
2) cutting on the total transverse energy in the event, often called S_T. This works because in Drell-Yan, S_T is usually of the same order as the dimuon mass. It (probably) doesn’t remove much QCD unless the isolation criterion is applied, and there will still be plenty of top background. It’s best for models where the V is produced by a heavy particle (or particle pair) but the V momentum is often not high, the number of jets is rather small, and the events are rare.
3) cutting on the missing transverse energy in the event, which works because it’s small in Drell-Yan and QCD. This of course is done in many supersymmetry studies and elsewhere, but no model-independent limits on V production has been shown publicly. This is a powerful probe of models where some hidden particles are very long-lived, or often decay invisibly.
All of these approaches can be applied to muon pairs, electron pairs, photon pairs — even tau pairs and bottom-jet pairs, for that matter. Each of them can provide an advantage in reducing backgrounds and allowing more powerful model-independent searches for resonances. And in each case, there are signals that might have been missed in other analyses that could show up first in these searches. More theoretical and experimental studies are needed, but in my opinion, many of these searches need to be done on Run II data before there can be any confidence that the floor has been swept clean.
[There is at least one more subtle example: cutting on the number of tracks. Talk to me about the relevant signals if you’re curious.]
Of course, multi-lepton searches are a powerful tool for finding V as well. All you need is one stray lepton — and then you plot the dimuon (or dielectron) mass. Unfortunately we rarely see limits on V + lepton as a function of the V mass, but it would be great if they were made available, because they would put much stronger constraints on relevant models than one can obtain by mere counting of 3-lepton events.
A subtlety: The question of how to place cuts
A last point for the diehards: one of the decisions that searches of this type require is where exactly to make the cuts — or alternatively, how to bin the data? Should our first cut on the transverse momentum be at 25 or 35 GeV? and having made this choice, where should the next cut be? Without a principle, this choice introduces significant arbitrariness into the search strategy, with associated problems.
This question is itself crude, and surely there are more sophisticated statistical methods for approaching the issue. There is also the question of whether to bin rather than cut. But I did want to point out that we proposed an answer, in the form of a rough principle, which one might call a “2-5” rule, illustrated in the figure below. The idea is that a signal at the 2 sigma level at one cut should be seen at the 5 sigma level after the next, stricter cut is applied; this requires each cut successively reduce the background by roughly a factor of (5/2)². Implicitly, in this calculation we assume the stricter cut removes no signal. That assumption is less silly than it sounds, because the signals to which we are sensitive often have a characteristic momentum scale, and cuts below that characteristic scale have slowly varying acceptance. We showed some examples of this in section V of our paper.



18 Responses
Matt,
A few more thoughts. My previous post could be call the Enhanced Big Bounce (EBB) theory. It answers some tough questions and is a suggestion for Anna Ijjas’ “We need a new idea” statement.
1. Insensitive matter (Dark Matter) is preexisting universe matter (pum).
2. There is no antimatter theft as suggested by Janet Conrad. It is not needed to form our universe. (Maybe there is anti-pum matter).
3. The preexisting universe need not be of the same mass as our universe as is required for the Big bounce theory.
4. Our universe is inside the preexisting universe.
5. Pum external to our expanding universe caused the accelerating expansion of our universe. There is no mysterious “Dark Energy”.
6. Stars and galaxies formed earlier than expected.
7. What else?
An interesting implication is that Black Holes are not infinitely small singularities. They have a definite size based on their mass.
Matt,
I meant to say, if ordinary matter had a Planck length = .999 x preexisting matter Planck length.
Matt,
Thinking about a new idea will be very productive, although it takes a lot of time to piece together what we know and don’t know.
The February 2019 issue of Sky & Telescope indicates that the Big Bang theory is coming under a lot of scrutiny. For me, the biggest issue is missing antimatter which Janet Conrad at MIT said is the greatest theft of all time and the second issue is where “dark matter” (your insensitive particles) came from.
The only explanation I can come up with is that our universe was formed from the partial collapse of a preexisting universe and that our universe is inside that universe. According to Martin Bojowald”s “Follow the Bouncing Universe” article in the October 2008 issue of Scientific American, if a universe collapses there is a limit as to how much energy a finite amount of space can contain and when it is reached it will bounce into a new universe.
What he has declined to explain is why the collapsing universe had just the right amount of matter to bounce to form our universe. What is much more probable is that the preexisting universe had much more matter than needed and the bouncing new universe expanded inside the preexisting universe.
The momentum of the excess preexisting universe matter could have caused the Planck length of ordinary matter to be slightly shortened, thus limiting the detection of preexisting universe matter because the wavelengths of most of the radiation would be incompatible and mostly hidden in ordinary matter radiation.
The only way I can think of to detect this radiation is to look for a slight bump in emissions at an even multiple of wavelengths, for example, perhaps every thousand wavelengths if the Planck length was shortened by .999%.
Finally, it seems that the analysis of the subatomic data needs to be influenced by macro understanding of the origin of our universe. This may be why the present search has such limited results because it is influenced by an incorrect Big Bang theory.
“And if you’re a bit unconventional, you might wonder whether particles that are insensitive to all the known forces (except gravity) might have an unexpected role to play in explaining the mysteries of particle physics”
Matt,
It 85% of our universe is made of “insensitive particles” (dark matter) it is highly probable that your statement above is true. If the particles had a slightly longer Planck length than ordinary matter they would be extremely hard to detect.
Anna Ijjas at Harvard said two years ago that we need a new idea, so keep up your quest.
🙂 perhaps we need a new idea, perhaps we don’t. I’ve been thinking about this since 1998, and have numerous papers since 2006. And I’m not the only one.
please really try your idea with full data. it is not so difficult once you have an idea and you want to verify that.
As I tried to explain very clearly in my post, the full data is NOT PUBLIC, so we do not have access to the full data, making it literally impossible to carry out our idea on the full data. Only the experimenters, who have access to the full data, can do it, and we are strongly encouraging them to do it.
ok good luck.
the possibility of confirming it as a particle is very low. however once it is confirmed , it is big issue in physics
Agreed.
A veritable deluge of open data.
“you might wonder whether particles that are insensitive to all the known forces (except gravity) might have an unexpected role to play in explaining the mysteries of particle physics. Importantly, these (and only these) types of particles could have arbitrarily low rest mass and yet have escaped discovery up to now.”
So my naive expectation, which seem to be supported by the “decay” article [ https://profmattstrassler.com/articles-and-posts/particle-physics-basics/why-do-particles-decay/most-particles-decay-why/ ], was that such particles would be rarely seen in collisions and that is part of the reason why they escape such discovery.
Is the plan to try to put upper bounds on the role of putative hidden sectors? Or keep going as long as LHC generate data? Or something else entirely?
Such particles MIGHT be rarely seen; they could also have been common. The point is the following: with particles that carry the known forces, we know exactly or roughly how they are produced, and therefore can predict the rate at which they are produced; they cannot be arbitrarily rare. With particles that don’t carry the known forces, they could be common, or rare, or very rare. Yes, one should put the most stringent bounds on such particles as one can, as long as the LHC is generating data. If you don’t discover any, then success is measured by whether your search was as thorough as it could have been; otherwise you’re not done with your work.
the peak at 39 gev seems to have width of a few gev. this says it has short life time. how can it appear to be such off vertex event?
or maybe you mean even the 29 gev particle comes from the decay of much stable particle in your theory?
I do no understand this.
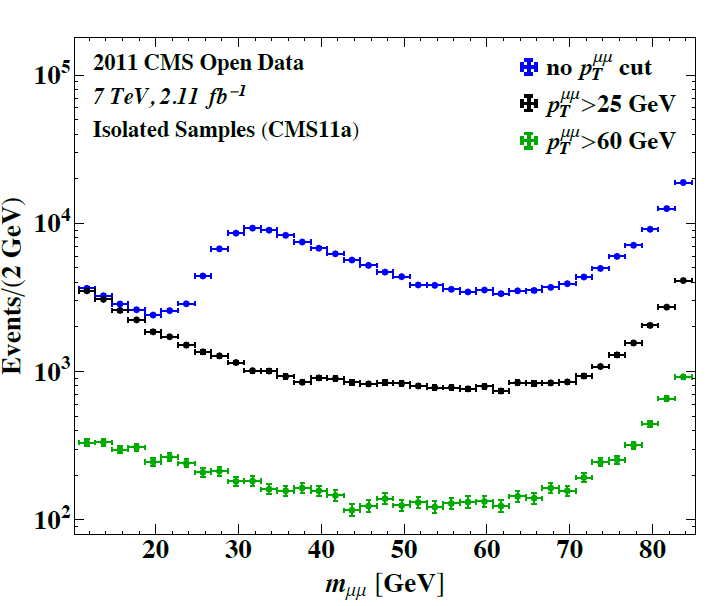
Width of a few GeV?!? What figure are you looking at? If you’re looking at the last figure, the bump there entirely a trigger effect seen in the pT>0 sample, and has nothing to do with the excess I’m talking about. If you’re looking at the next-to-last figure, you’ll see the bumps there are narrower than 1 GeV, but more than 0.5 GeV, because the detector’s measurements are not perfect.
next to the last figure? that kind of structure can rarely be seen as a particles. unless you agree that there are a lot more résonances. I am pretty sure when the data set is increased by a factor of 100, those 29 gev bumps will dissapeared. …
I’m sorry, but all indications are that you are misinterpreting the plots. Remember this section is for experts and I did not explain these plots carefully, assuming people who were reading this were experts and would understand them. The right figure is a *limit plot*, most or all of the bumps reflect statistical fluctuations. For example, see https://atlas.cern/sites/atlas-public.web.cern.ch/files/styles/large/public/field/image/0212-Dec2011-results-3a.jpg; one of those bumps in that plot is the Higgs (in retrospect) and all the others are statistical fluctuations. [Incidentally, our results were carefully examined by several CMS experts before we made them public; moreover we have received many additional positive responses from the CMS community since the paper appeared.]
The only statement I agree with is that the bump at 29.5 GeV will likely disappear with 100 times the data. The chance it is a real particle is extremely small — but not for the reasons you stated.