The Standard Model More Deeply: How the Proton is Greater than the Sum of its Parts

POSTED BY Matt Strassler

ON 07/22/2024

The mass of a single proton, often said to be made of three quarks, is almost 1 GeV/c². To be more precise, a proton’s mass is 0.938 GeV/c², while that of a neutron is 0.939 GeV/c².

But the masses of up and down quarks, found in protons and neutrons, are each much less than 0.01 GeV/c². In short, the mass of each quark is less than one percent of a proton’s or neutron’s mass. If a proton were really made from three quarks, then there would seem to be a huge mismatch.

(Here and below, by “mass” I mean “rest mass” — an object’s intrinsic mass, which does not change with speed. It is sometimes called “invariant mass”. [Particle physicists usually just call it “mass”, though.])

Part of the explanation for the apparent discrepancy is that a proton or neutron is, in fact, made from far more than just three quarks. In its interior, one would find many gluons and a variety of quarks and anti-quarks. However, that doesn’t resolve the issue.

Gluons, like photons, have zero rest mass, so they don’t help at all, naively speaking.
The typical number of quarks and anti-quarks inside a proton, while more than three, is too small to add up to the proton’s full mass;

And thus one cannot explain the proton or neutron’s large mass as simply the sum of the masses of the objects inside it. The discrepancy remains.

Moreover, as can be verified using either strong theoretical arguments in analogous systems or direct numerical simulations, protons and neutrons would still have a substantial mass even if the quarks and anti-quarks they contain had none at all! Mass — from no mass.

Clearly, then, the solution to the puzzle lies elsewhere.

Mass is Not “Conserved”

The essential point is that the mass of an object is not the sum of the masses of the objects that it contains. In physics-speak, mass is not conserved. Did you learn otherwise in chemistry class? Well, certain lessons of chemistry class are not exactly right, and in particle physics — and specifically, within your own body and within every object around you — they often do not apply.

There’s already a subtle clue in the mass of a simple hydrogen atom, made of just one electron and one proton. It differs very slightly, by about one part in 100 million, from what you’d get if you added together the mass of an electron and the mass of a proton.

Admittedly, it’s not obvious this has anything to do with the issues inside a proton. After all,

the hydrogen atom’s mass is very slightly less than the sum of the masses of the electron and the proton;
the proton’s mass is much greater than the sum of the masses of the objects inside it.

Nevertheless, these two facts are indeed closely related. I’ll go through the first one before explaining the second.

Both Einstein’s relativity and quantum physics are involved. We must keep track of the fact that electrons and quarks are not really “particles” — at least, not as we mean the word in English, when we apply it to specks of dust or particles of smoke. Instead, they have many wave-like properties. I often prefer to refer to them as “wavicles”, a term which was invented about 100 years ago, and I’ll do so in this post.

Wavicles, unlike ordinary particles, are vibrations; like any wave, they can have a vibrational frequency f, but unlike usual waves, they have an energy E that is proportional to that frequency. This is represented in the quantum formula: E=fh, where h is Planck’s constant, a constant of nature that serves as a conversion factor between E and f.
We must also accurately account for Einstein’s relativity equation, E=mc², a formula that relates the energy stored within an object to its rest mass m — and where c, the cosmic speed limit (also known as “the speed of light”), again serves as a conversion factor between E and m.

The key intuition we need is this: in contrast to an ordinary particle, a wavicle has the property that its frequency grows — and therefore its energy grows — when its container shrinks.

For instance, a wavicle in a hole has energy that depends on the width of the hole, as well as on the depth of the hole. This is unlike a particle’s energy, which depends only on the depth. As a result, a wavicle in a well will lose energy if the well is made deeper, yet it will gain energy if the well is made narrower. Both for atoms and for protons, this is crucially important.

Why is this true? If you want the back-story, you should read my two earlier posts comparing ordinary particles and wavicles:

The first post highlights key differences between particles, waves and wavicles.
The second post points out a consequence of these differences: a particle in a collapsing well will remain there to the end, while a wavicle will escape before the well collapses completely.

Atoms

Within a hydrogen atom, made of nothing but one electron and one proton, the proton pulls the electron toward it via the electric force. The smaller the distance between them, the stronger the pull.

This makes the electron behave as though it is on a edge of a very deep and steep 3-dimensional hole, with the proton at its center. I’ve sketched this in Figure 1. The horizontal direction represents the distance of the electron from the proton, while the vertical direction in the drawing showing the energy-depth of the “hole”. The little flat area is the location of the proton, where the hole terminates. (It is not to scale; the hole should extend off the bottom of your screen.)

Figure 1: If an electron were a particle, it would fall, thanks to electrical attraction, into the “hole” created by the proton; this would leave it sitting on or inside the proton, as in Fig. 2, having lost a large amount of energy in doing so. Not to scale. The dashed lines represent what the electron’s energy would be if there were no proton nearby.

If the electron were really a particle that could fall to the bottom of a hole, it would fall toward the proton until it reached the proton’s edge. After radiating away some excess energy, it would eventually settle down there, as in Fig. 2.

*Figure 2: If an electron were a particle (green), it would end up on or inside the proton (red), and its energy would be tremendously reduced.*

The electron’s energy would then have been reduced by the depth of the hole. And how deep would that be? Well, the electron’s internal mc² energy is about 0.000511 GeV. But in this hole, it would lose more than that, several times over! This means that the combined proton-electron system would have a smaller mass than the proton does on its own. (You can rightly worry about what that might lead to…)

But this is all heading in the wrong direction. An electron isn’t a particle, not of the conventional sort, anyway. It’s a wavicle. Squeezing it into a small region increases its frequency, and therefore its energy. As a result, its energy wouldn’t actually be reduced if it were shoved down into a deep but narrow hole; the energy would actually increase! And so an electron, unlike an ordinary particle, simply won’t allow itself to be forced into such a predicament; it won’t fall into the hole in Fig. 1.

What ensues is a competition between two effects:

the hole is trying to pull the electron in and reduce its energy,
but the further the electron goes into the hole, the narrower the space available to it, which increases its frequency and therefore its energy.

As shown in Fig. 3, these two effects balance, and a hydrogen atom forms, when the electron just dips its toe into the hole. In protonic terms, it ends up occupying a gigantic region — with a volume about 1,000,000,000,000,000 times larger than the volume of a proton! Said another way, the diameter of the electron, and thus of the hydrogen atom, is about 100,000 times larger than a proton’s diameter; the atom is 10^-10 meters across, while a proton’s diameter is a tiny 10^-15 meters.

Figure 3: In a hydrogen atom, the electron, as a vibrating wavicle (blue), remains very spread out, but falls just far enough into the “hole” created by the proton that it remains attached to it. A small but finite amount of energy would be needed to knock it free. Not to scale.

Note: this is different from what happens to a wavicle in a well with vertical walls, which I covered in a recent post. In a straight-walled hole, it’s largely all or nothing; either the wavicle is confined in the hole, or it isn’t. But here, the walls of the “hole” tail off very gradually, which permits the electron to spread out far and yet remain attached to the hole.

As is true for any object, the mass of the atom is its internal energy, divided by c². Most of the atom’s energy is obtained by adding the internal energy of the proton (0.938 GeV) to that of the electron (0.000511 GeV). But because the electron is (barely) inside the well created by the proton, just below the “level ground” that it would sit on if it were isolated, it has lost a tiny amount of energy: a mere 13.6 eV = 0.0000000136 GeV. (This is called the atom’s “binding energy.”) That in turn means that a hydrogen atom’s mass is 13.6 eV/c² less than the sum of the masses of the electron and proton.

Figure 4: The electron, as a wavicle, does not fall onto the proton, but surrounds it, with very slightly reduced frequency and energy. Not to scale; the proton is much smaller than shown relative to the electron.

It’s a tiny reduction, but without it, the hydrogen atom wouldn’t be stable — it wouldn’t remain intact. To break the atom apart, “ionizing” it so that the proton and electron separate from one another, requires 13.6 eV of energy be added to it. And so, unless and until someone or something provides that energy, the proton and electron will remain together in atomic form.

[Note: if you’ve seen this argued in terms of the uncertainty principle rather than using the approach I’ve used here, be reassured: these are two complementary views of the same phenomena, and they do not contradict one another.]

Seeing how an atom works now raises a puzzle. If the atom is stable because its energy is lower than that of its constituent parts, how can a proton, whose energy is higher than that of its constituent parts, be stable? I’ll answer that at the very end.

Click here for more mathy details on atoms

First, let’s see that the energy of an electron particle sitting on a proton would be reduced by more than its $mc^2$ energy. The electrostatic energy of an electron near a proton can be written

$E_{{\rm elec}} = -\frac{h c}{2 \pi} \frac{\alpha}{r}$

which is just a rewriting of the usual expression seen in first-year physics; here $\alpha$ is a number, approximately 0.007. If we put $r=10^{-15}$ meters, the radius of a proton, then

$E_{{\rm elec}} =- \frac{h c}{2 \pi} \frac{\alpha}{r} = -1.4 \ {\rm MeV} =-0.0014 \ {\rm GeV}$

which is a reduction in energy about three times larger than the electron’s $mc^2 = 0.511 \ {\rm MeV}$ .

Now let’s consider the electron as a wavicle in a box of length $L$ . The Compton wavelength of the electron is

$L_e = h / m c \approx 2.5\times 10^{-12} \ {\rm meters}$

The energy of a wavicle in a box of length $L$ is roughly

$E = \sqrt{ (mc^2)^2 + (hc/L)^2}$

where I am not keeping track of factors of 2 and other details, but just capturing the essence of the phenomena. If the box is large, with $L \gg L_e$ , then the first term is larger than the second, and we can approximate the electron’s energy using the fact that if $y\ll x$ , then

$\sqrt{x+y} \approx \sqrt{x} + \frac{y}{2\sqrt{x}}$

and so

$E \approx mc^2 + \frac{h^2}{2mL^2} \ .$

Maybe this reminds you of the expresssion for a slow particle’s energy in special relativity, where the second term is the particle’s kinetic energy, written in terms of its speed $v$

$E \approx mc^2 + \frac{1}{2} mv^2\ .$

Indeed, we should understand the second term as a wavicle’s kinetic energy, where $v$ is replaced by $h/mL$ . This is how quantum physics works; this conversion from speed to shape underlies the Schrodinger equation.

If the electron is roughly at a distance $r$ from the proton on average, then perhaps we can think of it as being in a box of size $2r$ , with a depth $E_{elec}$ ? We should not expect this to be strictly accurate! A hole shaped like the one in Figure 3 is far from a simple box! Nevertheless, keeping this in mind, let’s proceed.

The total energy of the electron, under this guess, is then

$E \approx mc^2 + \frac{h^2}{2m(2r)^2} \ -\frac{h c}{2 \pi} \frac{\alpha}{r}$

The first term is independent of $r$ . The second grows positive when $r$ is small, while the third grows negative when $r$ is small. The balance point between these last two effects, where $E$ is smallest, is at

$\frac{h^2}{4mr^2} \ = \frac{h c}{2 \pi} \frac{\alpha}{r}$

or, being careless with factors of 2 and $\pi$

$r\approx \frac{\pi}{2}\frac{h}{c} \frac{1}{m\alpha} \approx 1.5 L_e/\alpha$

This answer turns out to be too big, by about a factor of a few, mainly because our approximation, in which we treated the hole as though it were a simple box, isn’t sufficiently valid; there are some $2\pi$ factors to account for. But it captures the essence of the physics — the atom forms through a balancing act that prevents the wavicle from sinking to the bottom of the hole.

To check this reasoning is really correct, it’s time to sit down and solve quantum physics equations and do some hard work. At the end of that effort, one does indeed find detailed energy levels, and an atomic radius, that matches precisely with experiments on hydrogen.

See also this argument which gets the same answer, within a factor of 2, via an even simpler approach.

One more thing: What would hydrogen be like in a universe with electrons of even lower mass? Such electrons would spread out even further, and the decrease in their energy would be less. The smaller the mass of an electron, the larger its atoms, and the less energy would be required to ionize them.

This means that electrons with zero rest mass could not form atoms at all! They would be infinitely large and infinitely easy to ionize.

And that, in turn, is why the Higgs field is so important for our existence. Without it, electrons would have no rest mass, and stable atoms would not exist.

Protons

A proton presents a puzzle. We’ve seen that the electric pull of the proton on an electron lowers the electron’s energy. How can we use a pull to hold an object together and yet give a wavicle higher energy, and lots of it?

Within a proton, the quarks, gluons and anti-quarks are all pulling on each other via the strong nuclear force. When the distances between them are much smaller than a proton, the strong nuclear force is similar to the electric force, only somewhat stronger: it makes them behave as though they are within a deep, narrow “hole”, where their energy falls rapidly as they approach each other.

But when they try to separate from one another, something new happens; the hole’s walls, rather than sloping gradually outward as in Fig. 3, extend upward, preventing any escape, as in Fig. 5. The quarks and gluons are trapped.

[A reminder about what is plotted in Fig. 5, as in Figs. 1 and 3: the horizontal direction represents the distance between a quark and, say, an anti-quark, but the vertical direction represents energy, not a vertical direction of space. So the picture conveys that the energy between the quark and anti-quark is growing very rapidly as they separate… very different from the gradual die-off of the energy seen in Fig. 3 that allows an electron to move far from a proton.]

The high wall changes everything. The “hole” that contains the wavicles is very narrow, and if the walls were absent or low, the quarks and gluons would easily escape, or at least spread out, as in Fig. 3. But thanks to these walls, the quarks and gluons find themselves stuck inside the hole.

Figure 5: In contrast to an electron in an atom, a quark or gluon in a proton acts as though it is in a narrow hole with towering walls. This traps it and forces its frequency and energy upward, well above what naively would be “ground level” (dashed line.)

Moreover, the trap remains extremely narrow as one climbs the walls, which the wavicles, figuratively speaking, attempt to do. This raises their energy to the point that it’s the width of the trap, not the masses that the quarks themselves carry, that determines how much energy the quarks have — and it greatly exceeds their E=mc² energy! Gluons, which have no mass, get all their energy from the trap.

[Specifically, the trap is much narrower than the Compton wavelength of the quarks. This is unlike the situation for an electron in an atom, where the electron can spread to an extent much larger than its Compton wavelength. The math of this is discussed in an aside below.]

In other words, it is the trap’s effects on the wavicles, not the masses of those wavicles, that provides the majority of the proton’s internal energy. That’s why a proton’s mass can be so much larger than the mass of the objects that it contains.

In fact, inside this trap, a quark’s energy would be almost unchanged even if its mass were zero. Since both gluons and quarks would still have a plenty of energy, a proton would still have mass even if its quarks had none! All that’s needed to generate considerable energy for the wavicles in the “hole”, and thus mass for the full collection of wavicles that make up a proton, is that the “hole” be narrow and that it have high walls that prevent the wavicles from escaping. And that’s what the strong nuclear force achieves.

Such are the deep secrets that lie at the heart of every atom. Without them, the proton and neutron would be a shadow of their true selves. Our existence depends upon this remarkable, intricate interplay of the strong nuclear force, Einstein’s relativity and quantum physics.

Click here to see more mathy details for the proton

You’ll want to look first at the related discussion about electrons in atoms, located at the end of the “Atoms” section.

The main difference for what happens in a proton versus what happens in an atom is that here the box is smaller than the quarks’ Compton wavelength. As a result, in the expression for the energy of a wavicle in a box,

$E = \sqrt{ (mc^2)^2 + (hc/L)^2}$

the second term is now much larger than the first. Expanding the square root as before, but in the opposite way, gives us

$E \approx {hc/L} + \frac{(mc^2)^2}{2hc/L)}$

The contribution of the first term involves the diameter of the proton, which is approximately $2\times 10^{-15}$ meters, and gives us an energy per wavicle that corresponds to a good fraction of the mass of a proton! (As for electrons in atoms, this gives a bit of an over-estimate, thanks again to some 2’s and $\pi$ ‘s.)

The second term is zero for gluons, and for quarks, it is so small by comparison to the first term that it can be largely ignored. Almost all the energy is coming just from the fact that $L$ is small.

As before, this estimate, while far from precise, captures the heart of the phenomenon: merely by creating a small box for the quarks and gluons to live in, the strong nuclear force produces a proton with a mass much larger than the masses of its ingredients.

To conclude, here are answers to two questions that I’m sure many readers will ask.

Wait! What About The Other Picture of a Proton?

Those of you who’ve read my book, or read elsewhere on this website about protons, will no doubt have noticed that this picture looks very different from the one I usually present, in which the inside of a proton is a maelstrom of quarks, gluons and antiquarks running about at or nearly at the cosmic speed limit, smashing into each other, and appearing and disappearing.

*Figure 6: Snapshot of a proton from my book,* *showing many quarks, anti-quarks and gluons as particles, moving around at high speed. © M. Strassler*

The difference between them is a classic example of how one transitions from a particle picture to a wavicle picture.

There’s an analogue here for atoms, too. Before the correct picture of an atom, shown in Fig. 4, was discovered, there was the Bohr model of the atom, which captured some of its properties. This model is presented in any first-year physics class (sometimes without explaining its limitations!) In that early picture of an atom, an electron is a particle, not a wavicle; it travels on a path that orbits the proton, and so its behavior is somewhat like a planet orbiting a star, except that it has to follow strange, inexplicable rules. One can go from the Bohr picture to the true, quantum picture in stages; the Bohr view is a good stepping stone, but it has flaws that are uncorrectable in the end.

*Figure 7: In the Bohr model of atoms, electrons (blue) are particles traveling on paths around the nucleus (red), not vibrating wavicles as in Fig. 4*.

The picture I usually give of a proton is somewhat like the Bohr model of the atom: it treats the quarks, gluons and anti-quarks as though they were particles, not wavicles. Like the Bohr model, it captures some of the story. In particular, it correctly illustrates these points:

a proton is far more complicated than an atom;
the energy of particles inside the proton is far greater than their E=mc² energy;
it is impossible to say how many quarks, gluons or anti-quarks are inside a proton
- though there are always three more quarks than anti-quarks

But as with the Bohr model of the atom, the reasons it gives to explain these three key facts are not complete or accurate. The correct picture is only obtained by treating the quarks, anti-quarks and gluons as the wavicles that they truly are. Then one learns that:

it is the strong nuclear interactions among the wavicles that make the proton complicated and turn it into a prison;
the reason that the wavicles inside a proton have so much energy is that the proton, for them, is a tiny prison, far smaller than their Compton wavelengths;
the patterns of wavicle interactions (which can create or destroy gluons, and convert quark/anti-quark pairs to gluons and vice versa), combined with a quantum physics effect known as “superposition”, assure that a proton simply does not have a definite number of quarks, of anti-quarks, or of gluons
- nevertheless, the number of quarks minus the number of antiquarks is definite, and equal to three.

Why did I leave this important story out of my book? The reason is simple: there wasn’t room for it. But… that’s why I have a website! What couldn’t fit in the book fits here.

Wait! Why is the Proton Stable?

Now we know why the proton is greater than the sum of its parts: the strong nuclear forces among those wavicles creates a high-walled, narrow trap. But why doesn’t the proton fall apart? If the energy of the individual quarks and gluons is smaller than that of a proton, how can the latter be stable?

This is far from obvious, and is directly related to why the walls of the hole stretch so far upward. Understanding how the strong nuclear force does this has been worthy of Nobel Prizes.

It turns out — I have written about this before — that it is impossible to isolate a quark on its own. If you try to isolate a quark, you will have to supply a huge amount of energy — so much that nature will co-opt it. Despite your best efforts, nature will take some of that energy and spontaneously create additional quarks and gluons and antiquarks in the vicinity of the quark you’re trying to isolate. In this way, nature itself assures that your effort will fail!

This effect is sometimes (and somewhat incorrectly) called “quark confinement” (for in truth it involves confinement of the strong-nuclear-electric field, or “chromoelectric” field.) The existence of the high walls in Fig. 5 is itself a consequence of this effect.

What this means is that a quark or gluon is never found outside a narrow deep “hole” with high walls… and therefore, all objects made from quarks, anti-quarks and gluons have mass greater than the masses of the quarks and anti-quarks that they contain.

Again, this cannot happen for atoms. You couldn’t have a hydrogen atom with more energy than an electron and a proton have separately, because the atom would instantly disintegrate; the electron and positron could reduce their energy by rushing apart from one another. But the quarks and gluons in a proton cannot escape each other; when they try, more quarks and gluons are made, requiring even more energy. Consequently, a proton cannot break into its component parts, even though those parts, treated individually, have less mass than does the proton itself.

Atomic Physics, Particle Physics, Quantum Field Theory
cx atoms, gluons, proton, quarks, wavicles

Share via:

27 Responses

Steven Guderian says:

August 27, 2024 at 4:00 PM

Dr. Strassler,

This is a very educational paper. I have just started on your book. I am betting that I will soon read some of the background information you referred to in this paper. And maybe get my questions answered.

Since individual quarks cannot be isolated how were the wavelengths of quarks determined to verify that they are not exceeding their Compton wavelength? Am I also correct in presuming that the six different quarks have different wavelengths since they have different rest masses/energies?

Also, if the rest mass/energy of the proton fluctuates, then does the energy difference at the electron also fluctuate? Wouldn’t this restrict the numbers and actions of the individual quarks inside the proton? Lastly, what mechanism allows for individual quarks inside the proton (and neutron) but not outside these nucleons?

Thank you Dr. Strassler, I am anxious to read further in your book where I am sure you will inspire more questions.

Loading...

Reply
1. Matt Strassler says:
  
  August 29, 2024 at 9:58 PM
  
  Yes, the quarks have different Compton wavelengths. Actually measuring them is very tricky, and four different methods have to be used (one for top quarks, one for bottom and charm quarks, one for strange quarks and one for up and down quarks, though the last two are closely related.) I’ve mentioned some of them here: https://profmattstrassler.com/2022/07/14/celebrating-the-standard-model-atoms-quarks-and-the-strong-nuclear-force/
  
  Now we turn to subtleties of quantum physics and how quantum states work. Since the proton is a stable quantum state, its energy is determined and does not fluctuate. However, this state consists of a superposition (remember Schrodinger’s cat, in a superposition of live and dead) of states that have different numbers of quarks/antiquarks/gluons and locate them in different places. This superposed combination of states IS the proton state.
  
  Quarks are never found outside of protons and other proton-like objects for reasons detailed in the last few paragraphs of this post; you may want to read the last section again with this question in mind.
  
  Loading...
  
  Reply
Cargo says:

August 12, 2024 at 6:35 PM

Michael Loss has written notes about stability of matter. He assumes the Fourier connection between position and momentum, and then he uses the “Coulomb uncertainty principle” to obtain the unique(!) ground state energy of the hydrogen atom. The same method can be used to calculate the Bohr radius – without the Schrödinger equation. What a beautiful mathematical result 🙂

Loading...

Reply
sinaneren@outlook.com says:

July 27, 2024 at 6:15 AM

… Aslında elektronun proton içine düşmesi veya girmesi nedeniyle güçlü kuvvetlerde azalma ve zayıf kuvvetindeki değişimi kuarklar ve gluonlarin elektron ile etkileşim ile açıklanabilir mi? Elektronun cekirdegin yakında geçmesi kuark ile elektron etkileşim neden olmaz mı? Bu etkileşim minimum ne kadar çapta (uzaklıkla) olması gerekiyor.

Loading...

Reply
Karl Young says:

July 24, 2024 at 10:17 PM

Hey Matt why didn’t anybody tell me this in 1986 ! 🙂 Seriously though, back then, and before all the Nobels and what went it to them, as an undergraduate I worked on a rather ingenious updated and automated version of Milikan’s experiment (devised by Roger Bland, a great experimentalist) aimed at looking for evidence of fractional charge. After measuring a substantial amount of material from
“likely” candidates (e.g. moon rocks), surprise, surprise, no statistically significant evidence for (free) fractional charge was discovered (though an experimentalist, who shall remain unnamed, had previously claimed discovery re. evidence of fractional charge). You (along with Gross, Wilczek, and Politzer et. al) have explained why our disappointing result was presumably the correct result.

Loading...

Reply
1. Matt Strassler says:
  
  July 24, 2024 at 11:01 PM
  
  Nobody told me back in 1986 either, when I myself was an undergraduate. I had to wrap my head around this as a graduate student in the early 1990s. It could have been explained to me earlier. But somehow the pedogogical techniques that I’ve used here hadn’t occurred to anyone yet.
  
  To be precise, I only explained to you what Gross, Wilczek and Politzer [following ideas of Symanski, Feynman and Bjorken] explained to the rest of us. I take no credit for the basic insights that they brought to physics, only for finding ways to make them more accessible to more people.
  
  By 1986, exposed fractional charge from quarks would have been a long shot. But in the 1970s, understanding was still limited enough that a search for liberated fractionally charged quarks made sense. Feynman had the right intuition, but it wasn’t proven. People became convinced by exhaustive experimental searches, numerical simulations that clarified the energetics, and theoretical arguments which agreed with both.
  
  But of course there could have been sources of fractional charge that aren’t from quarks, and so Bland’s experiment was and still would be worthwhile. The MilliQan experiment https://en.wikipedia.org/wiki/MilliQan_Experiment is looking for particles with charges roughly 1/1000 of an electron, which are well motivated by theoretical considerations and might exist.
  
  Loading...
  
  Reply
  1. Torbjörn Larsson says:
    
    July 25, 2024 at 7:26 AM
    
    Thanks for helping! That page supplied the volume integral for me, but the r factors seemed to simplify. Given that the uncertainty principle (say) implies the proton passing would proceed at high velocities – I think – it seemed reasonable at the time. (That page has a mean electron speed of 1/137*c, so it is surprisingly energetic even before the higher orbital states where relativistic effects can occur in larger atoms. E.g. the color of gold due to that, et cetera.)
    
    Having the simplest estimate of volume fraction is neat! It also fits the intuition your graphs support.
    
    Loading...
    
    Reply
Torbjörn Larsson says:

July 23, 2024 at 2:00 PM

The discussion of the proton as hydrogen nucleus made me interested, prompted by figure 3, of how much of the time the electron penetrates the proton.

Taking the 1s orbital Schrödinger wavefunction as (spinless) illustration, and noting small radius, it seems to simplify to ~ 10^-5 parts for the 10^-5 smaller nucleus!? [It’s bed time, so the likelihood is I made an oopsie somewhere …]

Loading...

Reply
1. Torbjörn Larsson says:
  
  July 23, 2024 at 2:13 PM
  
  Maybe “symmetrical” illustration was a better term.
  
  Loading...
  
  Reply
2. Matt Strassler says:
  
  July 24, 2024 at 11:32 AM
  
  The calculation you want is the probability of finding the electron inside the proton. Since the electron’s distribution is fairly constant across the interior of the atom, a good estimate is Volume(proton)/Volume(atom) ~ 10^{-15}. You can do this calculation precisely using the ground state hydrogen wave function (using formulas widely available, say at https://en.wikipedia.org/wiki/Hydrogen_atom ) and you’ll find
  
  ${\rm Probability \ to \ be \ in \ proton} = \frac{4}{3}\frac{r_p^3}{a_0^3}$
  
  where r_p is the proton radius and a_0 is the “Bohr radius” (i.e. the atom’s radius), confirming the estimate I made.
  
  Loading...
  
  Reply
Jason Stanidge says:

July 22, 2024 at 5:55 PM

What picture would you suggest to help visualize the disturbance of the electromagnetic field inside a stable Positronium atom?

My view is that the electromagnetic disturbance increases as the electron and positron approach one another so that the energy of the resulting pseudo-photon/disturbance etc subtracts from the energy of the electron and positron. Under Tim’s comment you say that energies add whereas I’m under the impression that we have to be careful to subtract the interaction energy in some cases.

Loading...

Reply
1. Matt Strassler says:
  
  July 22, 2024 at 6:02 PM
  
  Energies add, but some energies are negative — as in Figs 1, 3 and 5 in this post. Adding negative = subtracting.
  
  There’s nothing much more complicated in positronium (or hydrogen) than what we teach in 1st-year physics — not unless you want to account for very subtle effects like fine- and hyperfine-splitting. It’s just a -1/r electric potential modified by some slow time-dependence (i.e. slow compared to the speed of light, not slow by human standards.)
  
  Loading...
  
  Reply
Joseph says:

July 22, 2024 at 2:38 PM

An inverse square law for a force, allows objects to be separated, as a finite amount of energy is required to pull them apart. This equates to a 1/R potential. If the force law was only 1/R, instead of inverse square, this would require an infinite amount of energy to separate, as the force does not go towards zero fast enough. This would be a LN R potential.
What does the strong force law / potential look like? If it takes that much energy, to pull apart two quarks, that another quark pops into existence…..then the force law must be constant with distance, or even increasing with distance?

Loading...

Reply
1. Matt Strassler says:
  
  July 22, 2024 at 4:45 PM
  
  The potential is just like electromagnetism for very small R.
  
  If the quarks all have large mass, then the potential is linear in R at long distance and the force constant, for reasons explained here: https://profmattstrassler.com/2023/11/02/a-half-century-since-the-birth-of-qcd/ . Also confirmed in numerical calculations — here’s an old one from 2001, see Figure 2. https://arxiv.org/abs/hep-lat/0107021
  
  Because some of the quarks in our universe have small mass, the potential is a more complicated thing, because the energy density between the quark and anti-quark is enough to pop quark-antiquark pairs out of the vacuum (see https://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-known-apparently-elementary-particles/jets-the-manifestation-of-quarks-and-gluons/ ), making the notion of “potential” ill defined. The effect is that the quark and anti-quark potential effectively goes from 1/R to R to constant.
  
  Loading...
  
  Reply
  1. Eric Roche says:
    
    August 21, 2024 at 12:10 AM
    
    Thanks for writing Waves In An Impossible Sea! It’s really great work.
    
    I didn’t catch (probably missed/didn’t understand) a reason why these principles can’t scale indefinitely as long as certain criteria are met (e.g., shared binding energy, stability).
    
    Could a “stable” cosmological system ever act as one of these wells with gravity as the binding energy? A step further, could the relative energy of objects across that system be treated as a collective intrinsic energy if gravity interactions ensure the system will always remain intact?
    
    Loading...
    
    Reply
    1. Matt Strassler says:
      
      August 22, 2024 at 11:16 AM
      
      Since you also posted a similar question on https://profmattstrassler.com/waves-in-an-impossible-sea/waves-in-an-impossible-sea-commentary-and-discussion/going-beyond-the-book/ , I chose to answer it there.
      
      Loading...
      
      Reply
ADM says:

July 22, 2024 at 2:19 PM

Maybe there is a tiny black hole at the center of every atom that contains most of the atom’s mass and locks the atom together, strong force, via quantum gravity.

I bet the mechanisms for the macro black holes are similar to those in the atoms.

GUT?

Loading...

Reply
Bob Brzozowski says:

July 22, 2024 at 12:55 PM

“Wavicle in a well” – I love it! It seems to me to be superior to the common formulation of “a particle in a box” (both pedagogically and alliteratively).

Loading...

Reply
Mike Cox says:

July 22, 2024 at 10:52 AM

Bravo! Now I know what you were leading up to with your two previous posts. I had to reread the section labeled “Protons” multiple times, and maybe I will a few more, but the long walk to the conclusion was well worth the effort. Many thanks

Loading...

Reply
Joseph C Atwater says:

July 22, 2024 at 9:21 AM

In your reference to “Mass”, “The essential point is that the mass of an object is not the sum of the masses of the objects that it contains. In physics-speak, MASS IS NOT CONSERVED.
The question may be asked concerning the Law of the Conservation of Mass-which seems to defy such definition.
Agreed that the mass of an object is not the sum of the masses of the object it contains. If so , WHY is mass not conserved in every dimension, according to Law that Governs both Mass and Masses -Singular or Plural?

Loading...

Reply
1. Matt Strassler says:
  
  July 22, 2024 at 9:33 AM
  
  There is no universal “Law of the Conservation of Mass” in physics. This law, sometimes taught in chemistry classes, is an approximate law that governs chemical reactions specifically, and many simple physical processes in ordinary life, such as the collision of two ordinary objects. However, in subatomic physics, the law is badly violated. It simply does not work in nuclear reactions, for example.
  
  Just because something is called a “law” does not mean it is a fundamental law that applies in all situations. If the law of conservation of mass were true, you wouldn’t exist: for one thing, the sun wouldn’t shine. Nor could your electrons have gotten their masses from the Higgs field.
  
  The law of local conservation of energy-momentum is an example of a law that is believed to be fundamental and always true. The same is true of the conservation of electric charge. But there are many other conservation laws that are violated in some circumstances more than in others.
  
  Loading...
  
  Reply
Tim Preece says:

July 22, 2024 at 9:12 AM

It seems that the proton treated as an individual particle would be described by wavicle of relatively high frequency, although it is made from many quarks and gluons which have relatively low frequency.

Is it easy to see how many low frequency wavicles could combine to effectively make a single high frequency wavicle.

Loading...

Reply
1. Matt Strassler says:
  
  July 22, 2024 at 9:42 AM
  
  The question of how to understand composite wavicles, built from more elementary ones, is a complex one. We rarely actually have to work out the math for that in technical situations, which is fortunate, because it involves a very complicated mathematical transformation that usually can’t be done explicitly. However, the additions of frequencies is the easy part.
  
  Let’s first clarify your first statement: You said “although it is made from many quarks and gluons which have relatively low frequency”. Just to be clear, remember that frequency is energy, not mass, so the quarks and gluons have a substantial fraction of the proton’s frequency, much higher than their masses would suggest.
  
  Energies add: the energy of the proton is some of the energies that it contains. Frequencies do too, therefore. How does that work? You can already see this in trigonometric product formulas: if you have two waves with frequencies f_1 and f_2 and you superpose them, you get a wave with frequency f_1+f_2.
  
  $\cos[2\pi f_1 t] \cos[2 \pi f_2 t] = \frac{1}{2}\left(\cos[2\pi (f_1+f_2) t]+\cos[2\pi (f_1-f_2) t]\right)$
  
  The second wave, with the difference of the frequencies, cancels out when you do this correctly with exponentials
  
  $\exp[2\pi i f_1 t] \exp[2 \pi i f_2 t] = \exp[2\pi i(f_1+f_2) t]$
  
  If there are multiple wavicles, just keep multiplying.
  
  Loading...
  
  Reply
  1. Tim Preece says:
    
    July 23, 2024 at 9:14 AM
    
    Thanks. I think I need to think about this more carefully. Particularly why when we superpose the wavicles, we multiply the amplitudes rather than add them, and also if this still ok when there are multiple different fields ( quarks and gluons ) rather than just a single medium.
    
    Loading...
    
    Reply
    1. Matt Strassler says:
      
      July 23, 2024 at 10:59 AM
      
      The whole structure of quantum physics is built upon this multiplication.
      
      In any quantum theory (or even a pre-quantum theory), changes with time are caused by the Hamiltonian, which in turn tells you the energy. That means that if you have a state $\Psi$ of definite energy, the time derivative of the state equals the total energy of the state times the state itself — i.e., the Schroedinger equation:
      
      $i\hbar(d/dt)\Psi = E \Psi$
      
      If the state has a definite energy, then the solution is an exponential
      
      $\Psi \sim e^{-iEt}$
      
      But since energies add, components of a state must then multiply.
      
      Meanwhile there is the concept of superposition; perhaps we have a state which is a superposition of two states,
      
      $\Psi = c_1 \Psi_1+c_2 \Psi_2$
      
      where the first has energy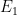 $E_1$ and the second has energy $E_2$ :
      
      Under the Schroedinger equation this evolves to
      
      $\Psi =\to c_1 \Psi_1 e^{i E_1 t} +c_2 \Psi_2 e^{i E_2 t}$
      
      showing that the energies in this case do not add: we have two branches of the wave function, each one with its own energy and evolving independently.
      
      In short: multiplication combines objects within a single, simple state, whose energies should be combined into a total energy; addition combines multiple states into superposed branches of a more complex state, each with its own energy.
      
      Loading...
      
      Reply
      1. Tim Preece says:
        
        July 29, 2024 at 10:10 AM
        
        I was thinking about the waviness of electrons and protons as revealed by the double slit experiment.
        
        Reading “Waves in an impossible sea” it seems that up-to-now-elementary particles like electrons are described by wavicles in an underlying electron medium ( as opposed to being pictured as wave functions ). However, for known-to-be-composite particles like the proton, it seems one has to go back to the wave function description in order to understand its waviness.
        
        I was hoping to picture the proton as a wavicle in an effective proton medium, maybe seeing how the underlying quark/gluon wavicles combine together, but without going back to thinking in terms of QM wave functions.
        
        I think I need to read a text book on this. I’ve just started reading a book on the Standard Model by Ken Barnes which will hopefully help me with more of the details.
        
        Loading...
        
        Reply
        
        Matt Strassler says:
        
        July 29, 2024 at 11:15 AM
        
        [Caution: “electron medium” is speculative. “Electron field” we know well, but not its origin; we don’t know if it has its own medium, or even if it has a medium.]
        
        Complicated objects are complicated; you can’t get away from that. Instead of thinking about a proton, which is exceedingly complex, just think about an electron-positron atom (“positronium”), which is no more complicated than hydrogen in its structure and is made from just two wavicles (to a good approximation.)
        
        You can’t get away from the fact that positronium, unlike the positron and electron themselves, has internal structure. A wavicle has no internal structure, so if you want to treat positronium as a wavicle, you have to put its internal structure into the mathematics somewhere. Otherwise, you’re completely sweeping away the fact that positronium has an infinite number of excited states, just like a hydrogen atom.
        
        Since that internal structure involves correlations between the energies, momenta and other behavior of the electron and positron, simply visualizing them as two independent objects, instead of two correlated objects, is impossible. And therefore the language of quantum physics — not necessarily wave functions, which is optional math, but certainly superposition of quantum states, which is not optional — cannot be avoided.
        
        In short, you cannot get simplicity out of complexity unless you carefully arrange to ignore the complexity in an intelligent way, and in the process, you will have to deal with quantum correlations… even if you choose not to use the language of wave functions.
        
        A proton, needless to say, is even more complicated than positronium.
        
        So if you want to learn how this is done, focus on positronium, or the hydrogen atom, or an atom made from an electron and an anti-muon (as they’re all pretty much the same if you ignore the complexities of a proton and the slow annihilation of positronium.) When you fully understand how you would treat an atom as a wavicle, which describes its “center-of-mass” behavior, attached to some additional information that tells you about its internal structure, then you have the main idea.
        
        But complexity is complex. Two elementary objects are far more complex than one, because they can be correlated.
        
        Loading...
        
        Reply