This article represents a lightning introduction to the black hole information paradox. Many details are omitted for brevity; longer articles will (eventually) explain them. Also, caution! the current understanding of the problem is so confused that the very last portion of this article should not be considered reliable or stable — it is likely to change in future.
[I thank Professor Joe Polchinski for consultations on the physics and for checking my illustrations for errors.]
The Two Conflicting Theories:
Quantum Theory (sometimes called “Quantum Mechanics”) is the mathematics that is currently believed to underlie all physical processes in nature. It can’t be used to predict precisely what will happen, but only the probability for any particular thing to happen. But probabilities only make sense if, when you add up all the probabilities for all of the different things that can possibly happen, you find the sum is equal to one. A quantum theory where this isn’t true makes no sense. One consequence of this is that in a quantum theory, information is never truly lost, nor is it truly copied; at least in principle, you can always determine how a system started (its “initial state”) from complete information about how it ends (its “final state”). See Figure 1, which shows two particles colliding, and several particles exiting from the collision, carrying off, in scrambled form, the information about the nature and properties of the two initial particles.

General Relativity is the name for Einstein’s theory of gravity, in which gravity can be thought of as an effect of the warping of space and time. General relativity is not a quantum theory; it predicts exactly what happens, not probabilities for various things to happen.
It was gradually understood, over the years from 1915 to 1958, that extremely compact and massive objects form black holes. Gravity becomes immensely strong in their vicinity… strong enough to warp space-time dramatically, with the effect that any object that gets too close, and crosses the black hole’s horizon — a surface of no-return — can never escape. See Figure 2, which shows a black hole horizon forming when two shells of matter become sufficiently compact. The information about these two shells goes inside the horizon and never can come out… in general relativity.
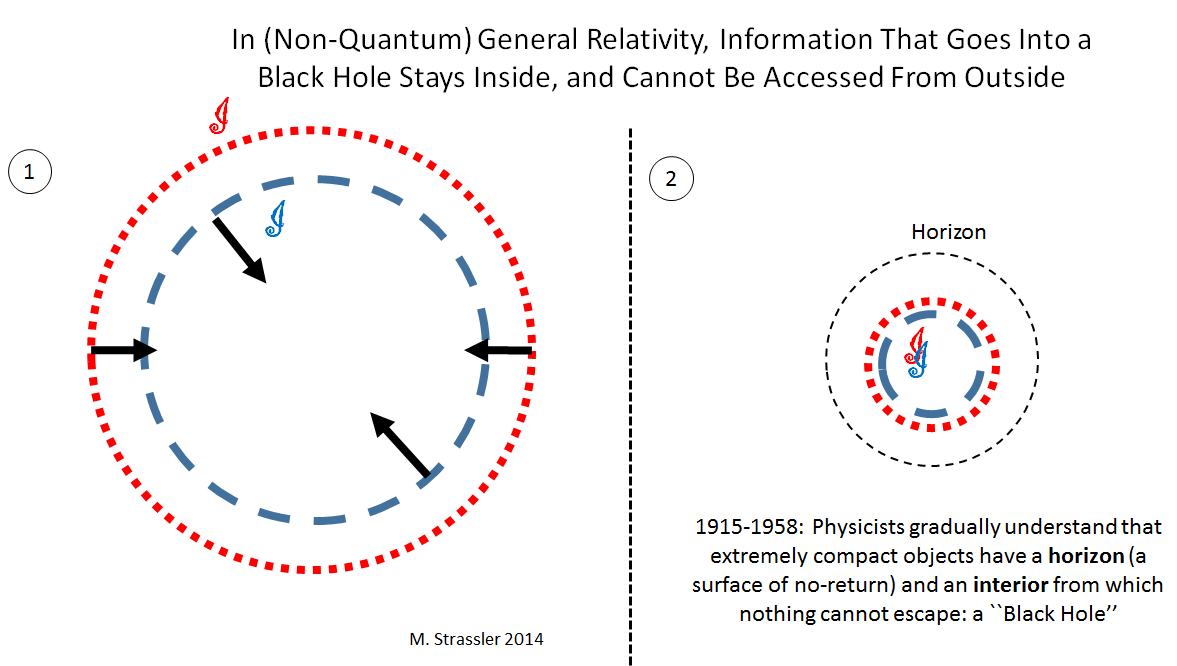
Caution! It is impossible to draw black holes, and the information inside them, without being misleading. My illustrations can’t illustrate how space and time are warped; for instance, to understand the whole story, you have to account for the fact that clocks inside the black hole run very differently from clocks just outside, which in turn run very differently from clocks far away. So don’t take my illustrations, which illustrate conceptual but not technical points, too seriously!
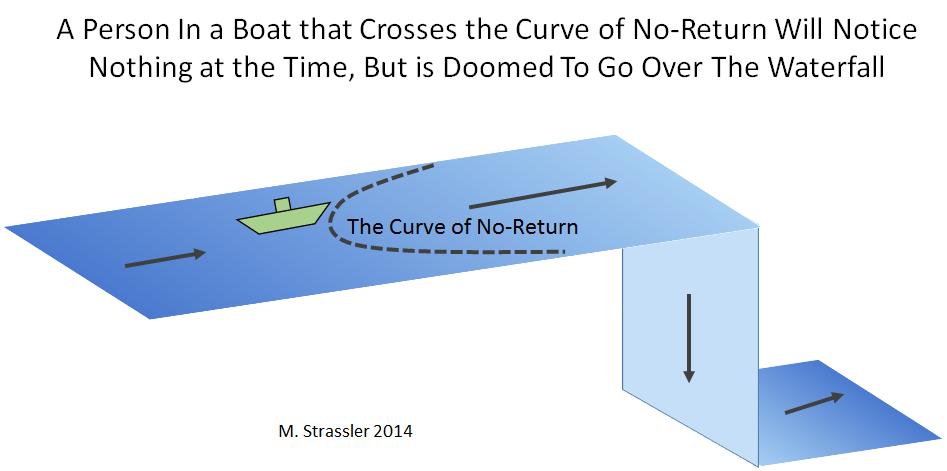
A horizon is not an object, but a place beyond which escape is impossible. A famous analogy is to a boat approaching a waterfall, in an increasingly fast current. Once the boat passes a curve of no-return (see Figure 3), its engine will be unable to fight the current, and it will inevitably go over the waterfall. But the captain of the boat will not notice anything when crossing this curve; it is just an ordinary part of the river, whose importance will only become clear when the captain seeks to escape disaster. Similarly, in general relativity you will notice nothing when crossing the horizon; it’s only when you try to escape the black hole that you will discover that — oops! — you went too close.
The “Black Hole Information Paradox”
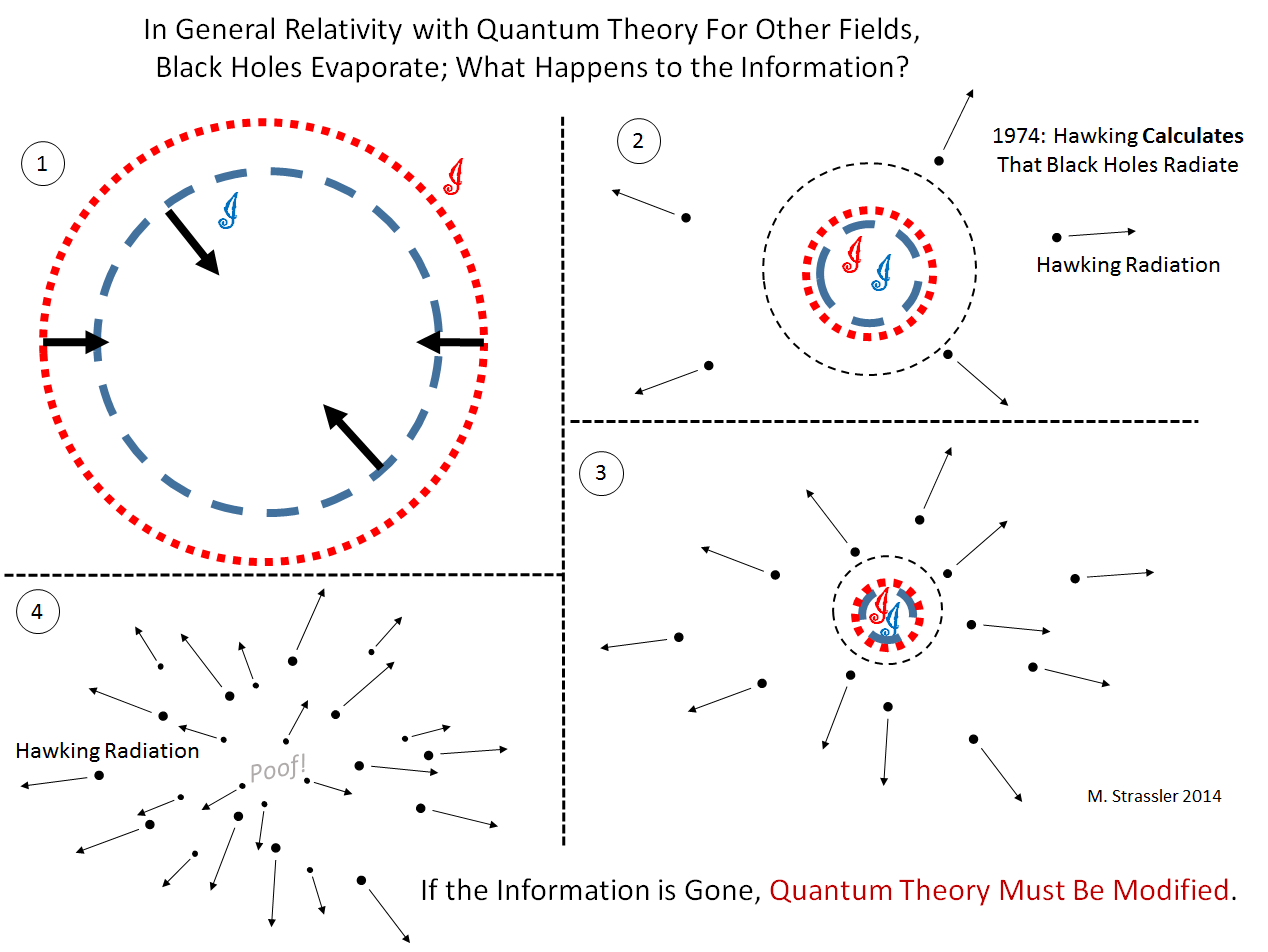
The paradox arose after Hawking showed, in 1974-1975, that black holes surrounded by quantum fields actually will radiate particles (“Hawking radiation”) and shrink in size (Figure 4), eventually evaporating completely. Compare with Figure 2, where the information about the two shells gets stuck inside the black hole. In Figure 4, the black hole is gone. Where did the information go? If it disappeared along with the black hole, that violates quantum theory.
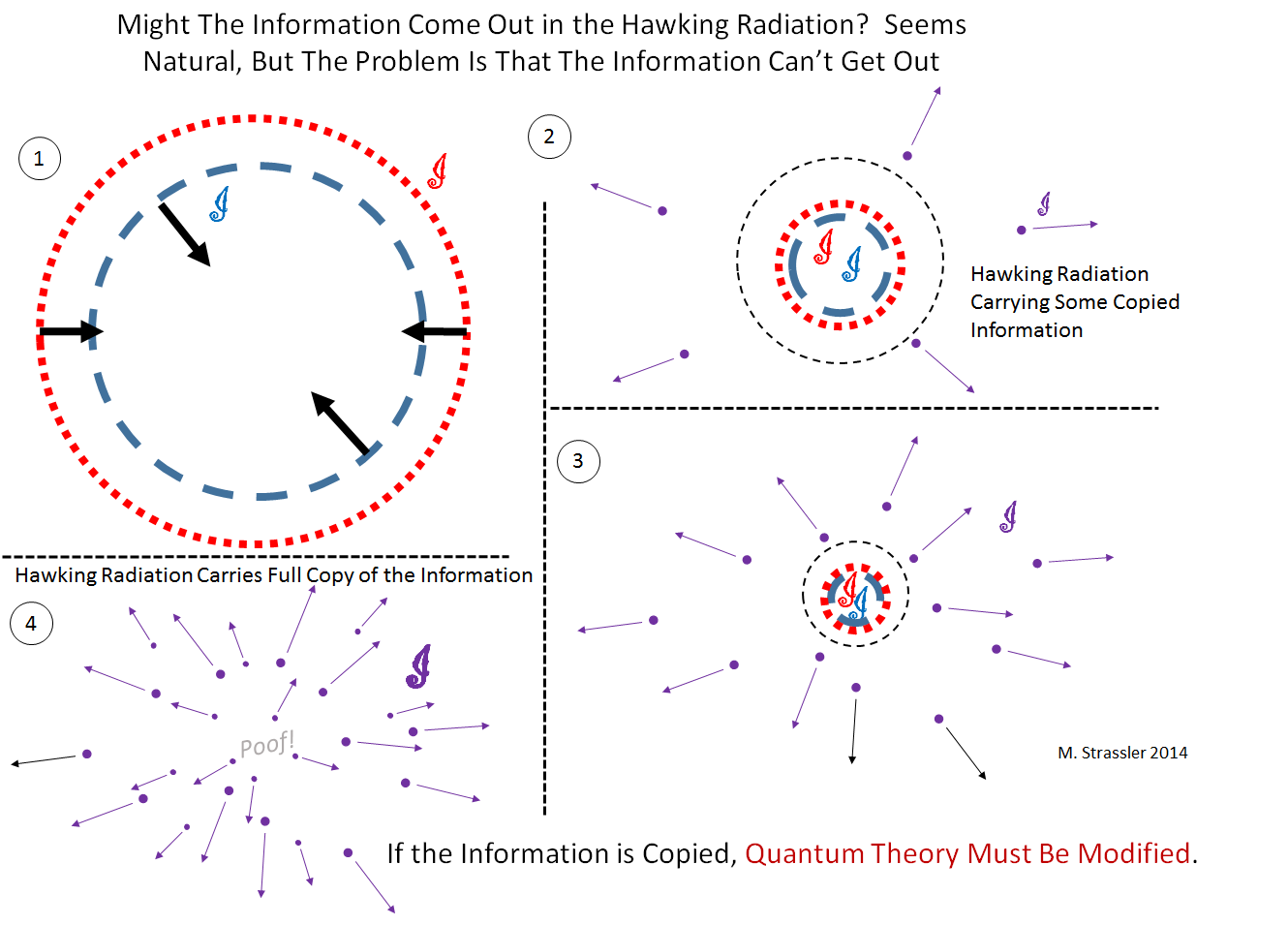
Maybe the information came back out with the Hawking radiation? The problem is that the information in the black hole can’t get out. So the only way it can be in the Hawking radiation (naively) is if what is inside is copied. Having two copies of the information, one inside, one outside, also violates quantum theory.
Of course, it may simply be that quantum theory is incomplete, and that the physics of black holes forces us to extend that theory, much as Einstein extended Newton’s laws of motion in his theory of relativity. And this is what Hawking believed for three decades.
Complementarity: Saving Quantum Theory
However, others felt that it was general relativity, not quantum theory, that would need to be changed. And a proposal was made in 1992, called “complementarity”, that suggested that the information was, in a sense, both inside and outside but without violating quantum theory. (This proposal was developed by Susskind and his younger co-workers.) Specifically, observers who remain outside the black hole see the information accumulate at the horizon, and then come flying outward in the Hawking radiation. Observers who fall into the black hole see the information located inside. (See Figure 6.) Since the two classes of observers cannot communicate, there is no paradox.
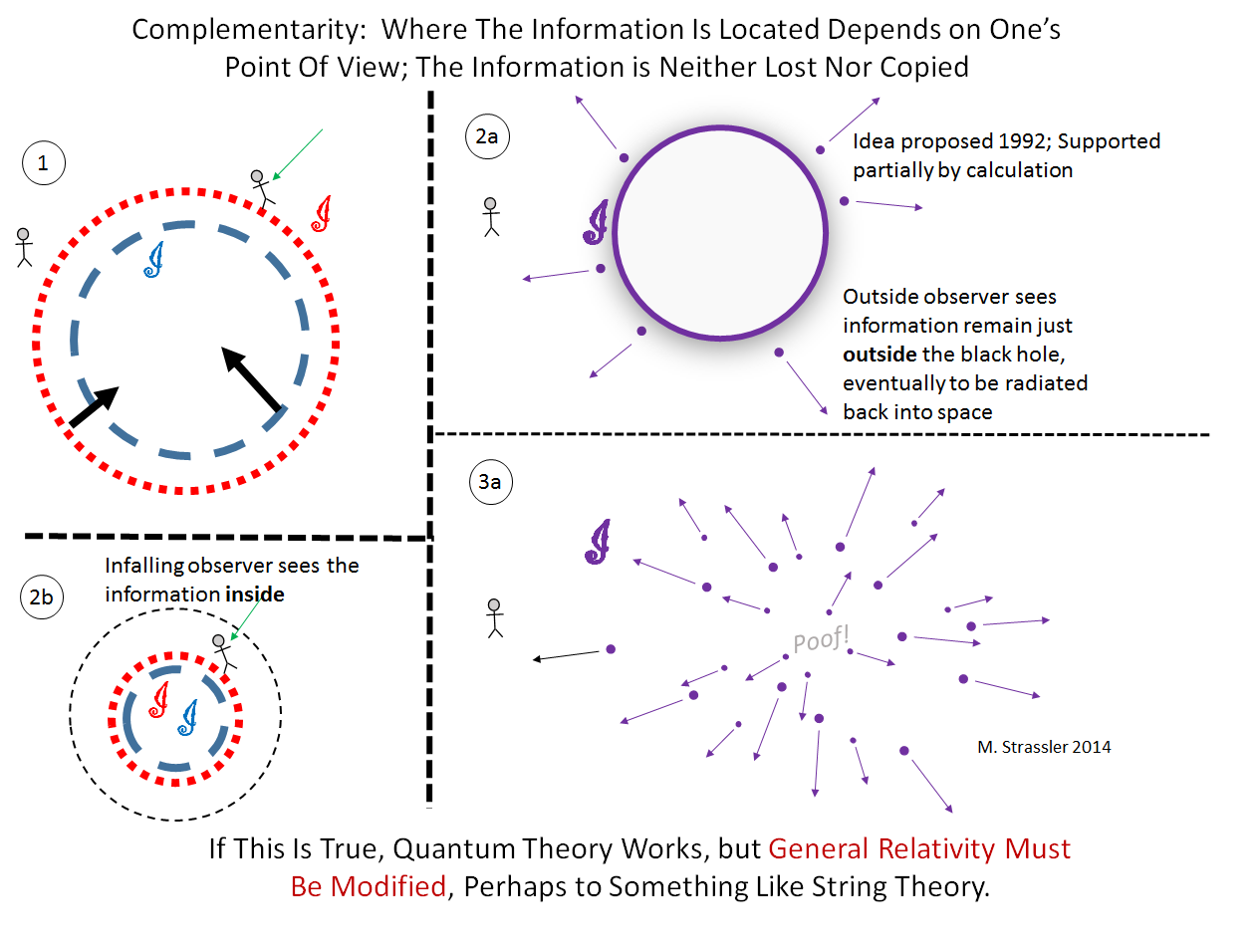
Still, this suggestion is potentially self-contradictory, and requires a number of strange things be true. Among them is something called “holography”, an idea developed by ‘t Hooft and further by Susskind. The idea is that the physics of the three-dimensional interior of the black hole, where gravity obviously plays a role, can instead be viewed, via a rather mysterious transformation, as physics just above the two-dimensional horizon, where it is described by two-dimensional equations that do not include gravity at all! See Figure 7.
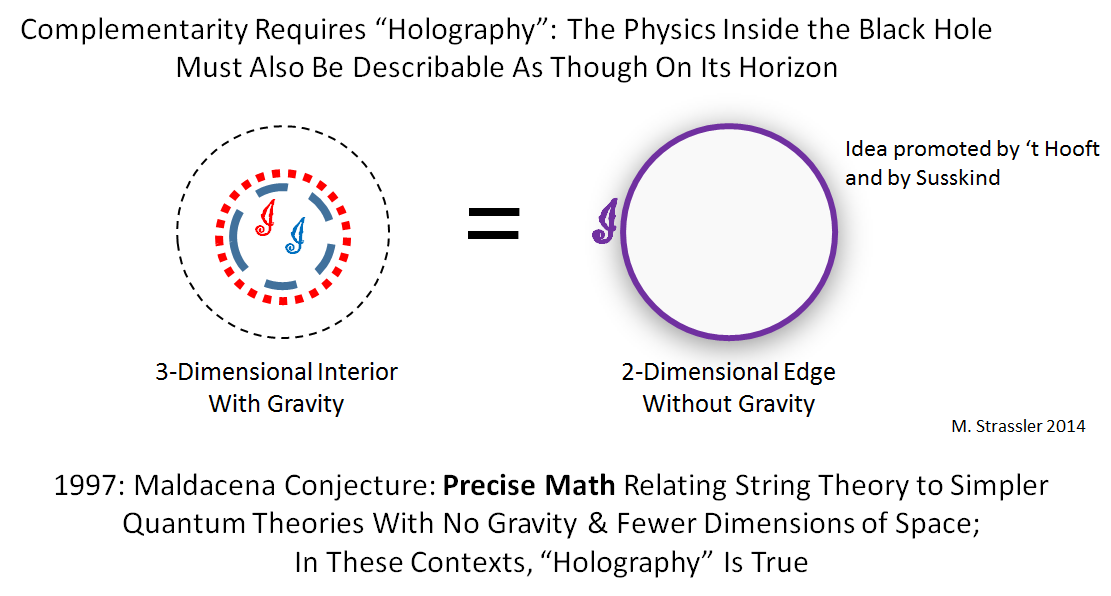
Crazy at it sounds, considerable evidence arose in the late 1990s that it is true, at least in some situations! In 1997, Maldacena conjectured (and hundreds of people checked, in various ways) that under the right circumstances, string theory (a theory that is a quantum generalization of general relativity, and is a candidate for a theory of the laws of nature in our universe) is actually equivalent to a quantum theory (specifically, a “quantum field theory”) without gravity and with fewer dimensions. This relationship, known variously as “AdS/CFT” or the “field/string” correspondence, deserves an article all its own (stay tuned for that.)
The success of holography gave additional credence to the complementarity idea. Furthermore, the field/string correspondence allowed for a very strong argument (perhaps a proof?) that small black holes can form and evaporate in the string theory via a process that can be described by the corresponding quantum field theory (though not explicitly) — and which therefore, as in all processes in any quantum theory, does preserve information! By 2005, even Hawking had come around to this point of view — that in fact, as the complementarity proposal had suggested, black holes do not cause information to be lost, and that general relativity, but not quantum theory, must be modified.
The Firewall and the Current Turmoil
Still, there were loose ends in the complementarity proposal. Black hole evaporation is so subtle that there were still no quantum theory equations for complementarity that could describe the evaporation process. While trying to find such equations, Almheiri, Marolf, Polchinksi and Sully discovered that in fact (at least under reasonable assumptions) complementarity contains a self-contradiction, which shows up when a black hole has evaporated about halfway. The argument is extremely subtle, involving the kind of “quantum entanglement” that Einstein called “spooky” and that gets used in quantum computers. But crudely speaking, by the halfway point, so much information has departed the black hole in the Hawking radiation that there’s not enough left at the horizon for holography to represent the black hole’s interior. Consequently, instead of an in-falling observer smoothly entering the black hole through the harmless horizon, as in Figure 6, the observer finds there’s no interior at all, and does so the hard way, by being fried to a crisp by a so-called “firewall” that hovers just outside the horizon (Figure 8).
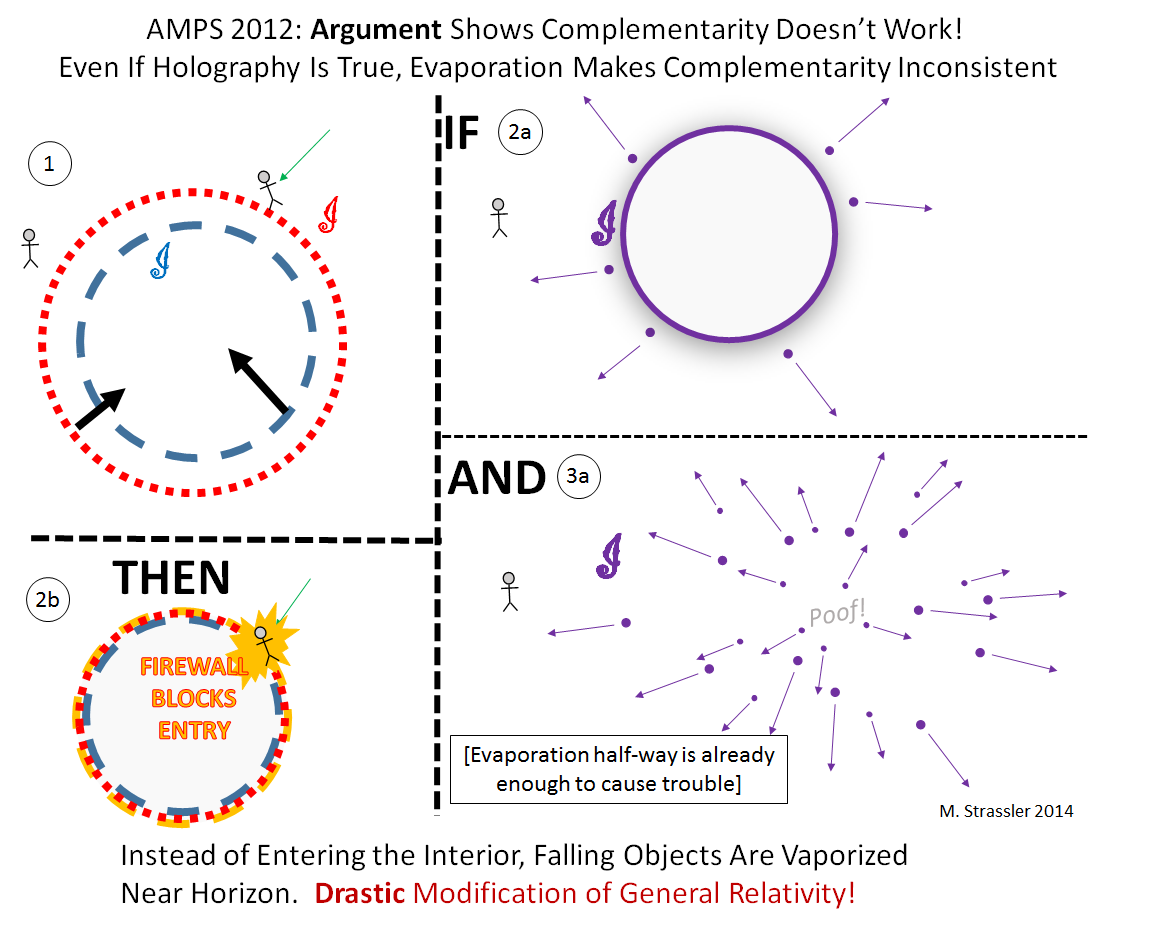
The possibility of a firewall would involve a very drastic modification of general relativity. It it were right, it would say that the picture provided of black holes by general relativity, that a black hole has a substantial interior, and that a horizon is nothing but a point of no-return (as in Figure 3) and not a place where special things happen as you pass it, is 100% wrong, once a black hole has done some significant amount of evaporating.
So now the paradox is baaaaack! And worse than ever. It seems that if quantum theory and complementarity are right, general relativity isn’t just requiring some small modification — it requires major surgery! And there’s no sign of such surgery in string theory, which provided the example of holography. But the field/string correspondence suggests quantum theory can describe black hole formation and evaporation, so information isn’t lost. So can complementarity be replaced with something else? Or is one of the arguments that creates this paradox actually wrong?
Everyone’s confused. There are lots and lots of proposals as to how to get out of this conundrum. You’re not hearing about most of them. The media told you about Hawking’s because he’s famous, but he’s really just one of many, many voices tossing ideas around. All of these ideas suffer from the same thing: not enough equations to provide evidence and details of how they’re supposed to work. And since not having enough equations is what led to the firewall paradox, we can hardly try to get out of this situation by relying on yet another argument that lacks equations for its details!
But even though Hawking is just one person making a proposal, and even though his proposal lacks equations and is likely to be, at best (in my view), incomplete, and more likely just wrong, you probably want to know what he suggested. It’s hard to figure that out without equations, but here’s my best effort (see Figure 9). Hawking points out that although exteriors of black holes quickly become simple, the interiors can become very complex. Complex systems, like weather, can exhibit chaos, which can make them unpredictable even before you think about quantum theory. He seems to suggest that the complexity itself destabilizes the horizon and allows the information, having been scrambled inside the black hole, to leak back out. Since this would violate Hawking’s own theorems about general relativity, I assume this means that general relativity must be modified. And since his argument rests on AdS/CFT (i.e. field/string correspondence), I assume he believes that this must occur in string theory. Since what went into a black hole does eventually come out, these holes are not really black after all — so call them “grey holes” or “metastable gravitational bound states” or “apparently-black holes”, but “black” is perhaps not really the right term.

But there are many obvious problems with this proposal — not the least of which is that the firewall puzzle shows up already after the halfway point of black hole evaporation, not just at the end of the evaporation. And thus the black hole is still very large when the information has to be leaking out — which would seem very difficult to reconcile with a proposal like Hawking’s. So don’t expect a consensus to grow around Hawking’s suggestion, especially not without some concrete equations to evaluate.
In any case, everything you learned about black holes is still basically true. Astrophysicists need not be concerned that there will be changes to what they think they know about stellar or galactic “black” holes. At least for a large and not-too-old “black” hole, Hawking’s proposal wouldn’t actually lead to any changes that you could measure. And if you fell in, you still couldn’t get out, nor could you realistically send a message to anyone outside. So even if it turns out that “there are no black holes” in the legalistic sense, there is still a spectacularly-dark hole to be found at the center of nearly every galaxy in the universe.
Don’t expect this 40-year-old puzzle to be resolved soon. And the resolution will probably come from a young physicist you’ve never heard of, or from a person not yet born.


262 Responses
The waterfall/whirlpool example was very helpful. It clarified that event horizon depend not just on the mass of the BH but also the cosmic speed limit
How does the cosmic speed limit influence the structure of in-falling matter as the curvature increases ?
For ex: gluon-quark interactions within a nucleus or proton electron interactions within an atom.
It seems particles moving in same direction will be stretched apart & particles moving in orthogonal/opposite direction will be ripped apart.
So there may not be a physical firewall but the cosmic limit in tandem with spacetime curvature seems to squash/rip-apart ‘matter’ as it approaches (or falls inside) black hole !?
In the last instant before a singularity is reached, tidal forces will become strong enough to rip apart a proton, yes.
But that singularity is nowhere near the horizon, and therefore nowhere near the firewall. It may be enormously distant.
There are no significant tidal forces, and there is no significant space-time curvature, at the horizon. A person falling in won’t notice. That is the whole reason for the “point of no return/waterfall” analogy; in classical general relativity, you don’t feel any large tidal forces, or anything else as you cross the horizon. And this is exactly why the idea of a firewall is so puzzling: it is a 100% rejection of a basic idea in classical general relativity.
So your questions in the first and last paragraph are inconsistent: the first asks about the effects of high curvature, and the other asks about what happens to objects when the approch or fall into the black hole. These are two completely different places, and so the answer to the first is “a lot happens”, and the answer to the second is “in classical general relativity, nothing happens”. In the same way, terrible things happen at the waterfall, but nothing happens at the point of no return.
At this point I always remind people that there is observational evidence that we do not live in an anti-de Sitter universe, and so that the AdS/CFT correspondence does not describe our actual universe.
In fact, I think you can regard the prediction of a negative cosmological constant as the one actual physical prediction to come out of string theory, and it has been observationally violated. My personal opinion is thus that AdS/CFT should be regarded as beautiful but wrong, and thus placed on the large heap of beautiful but wrong theories in physics. Of course, that is not a popular opinion in the particle physics community (it gets more support on the general relativity side), but I am a patient man.
Congratulations, Marshall: you have created a straw man, pulled out a bazooka, fired, and killed it. It was dead already, though.
I advise you to read quite a bit more. All you’ve shown here is that you have no idea how AdS/CFT is actually put to use in the field of high-energy physics.
In electrostatics, there’s an amazing theorem called the theorem of inversion mentioned on page 11 of Landau’s Electrodynamics of Continuous Media. With it, we can calculate the electrostatic potential at a point outside a spherical region of radius R from the potential at a point inside this region; but we need additional global information contained in the distance from the boundary R. The charge on the boundary of R can be calculated from Gauss’s law. Leading on to my question:
By the information being ‘copied’ to the outside, do you mean that the information inside and outside can be calculated from one another theoretically; but calculating this information at some point requires additional information that is distributed globally?
Is there an inversion theorem analogous to the above for general relativity and quantum field theory?
It is a captivating blog that delves into the intriguing concept of the black hole information paradox. The review commends the blog for providing a concise and accessible overview of this complex topic. It highlights the author’s ability to present the paradox in a comprehensible manner, making it engaging for both novice readers and those familiar with the subject. The blog effectively introduces key concepts and theories surrounding the paradox, sparking curiosity and inviting further exploration into the fascinating realm of black holes and the fundamental laws of physics.
How can information be preserved in quantum physics? You could only tell the past from information about particles if you could know that information (position and momentum etc) to an arbitrarily high precision. But doesn’t quantum physics say that you can’t know that information to an arbitrarily high precision, even in principle?
I wonder if I would not of took the mirrors out and the microwave and TV after the ride home, and removing my battery from the phone. Ummm….
Good afternoon, I was just checking out your website and submitted this message via your “contact us” form. The “contact us” page on your site sends you messages like this via email which is the reason you are reading through my message right now correct? That’s the most important achievement with any type of advertising, getting people to actually READ your ad and that’s exactly what I just accomplished with you! If you have something you would like to promote to lots of websites via their contact forms in the US or anywhere in the world send me a quick note now, I can even focus on particular niches and my costs are super reasonable. Send a message to: harry2947har@gmail.com
Good day!
You Need Leads, Sales, Conversions, Traffic for profmattstrassler.com ? Will Findet…
I WILL SEND 5 MILLION MESSAGES VIA WEBSITE CONTACT FORM
Don’t believe me? Since you’re reading this message then you’re living proof that contact form advertising works!
We can send your ad to people via their Website Contact Form.
IF YOU ARE INTERESTED, Contact us => lisaf2zw526@gmail.com
Regards,
Sparkes
I thank you for this attempt to popularize this paradox. I would have appreciated a brief definition of what you mean by information in your article. This term is used in the first paragraph without being defined. That would make it clearer, wouldn’t
I am beginning work on the paradox at this time.
Just saw this. As a retired experimental particle physicist I try to get the gist of cosmological statements, and this “information paradox” , seems to me strange. You say : “information is never truly lost, nor is it truly copied; at least in principle, you can always determine how a system started (its “initial state”) from complete information about how it ends (its “final state” “. . Isn’t the density matrix formalism with its inevitable decoherence a “proof” that going from quantum to classical ,information is lost? Why this cannot work at the horizon inputs and outputs?
forgot notification
Isn’t the information dependent upon observation? One of the postulates of QM is that upon measurement the state will collapse into one of the eigenvalues corresponding to the state wave. Are there not infinite possibilities of this information before observation? If so, wouldn’t the information also be emitted with infinite possible results of variable information unless observed/operated on beforehand? Or is this just what he is stating in the “Complimentary: saving quantum theory” section when he describes the information being frozen at the even horizon until evaporation is complete?
Professor, would it be fair to say that blackholes (BH) are still poorly understood? For example, a more ‘simple’ questions in my amateur scientist’s mind: What would the nature of the matter inside a BH be, or would you find any matter at all or just energy. In my understanding, a BH’s gravity would accelerate matter to the speed of light at the event horizon – but to actually reach the speed of light seems impossible for matter, because a infinite amount of energy was needed to do that. So wouldn’t we already hava problem there, that the BH would try to accelerate the matter to the speed of light, but can never succeed in doing so. So they kind of get stuck unless matter is somehow transformed into something that can actually reach the speed of light (like photons, neutrinos,…?). What would I have to read to find the answer to how science treat this problem – or whether they consider it a problem at all…?
Can you suggest a book which gives somewhat details about this topic ?
I’ve just read through your cosmology sections and want to say thank you very much. As merely a long interested layperson it may seem ridiculous to most that I have been wrestling with many of the questions re where did it come from and where does it go, the apparent similarities between the event horizons at each end and how something can get bigger without expanding into nothing or meeting itself!
Unsurprisingly, I’m none the wiser but much better informed and marvel at how much we can know while the dragons beyond the hills never had it so good – truly an inspiring and exciting time for exploration!
Hello, I would like to ask question, what if the law of conversation of energy is valid only in our universe ?
Because everything was generated in big bang (energy, matter, we) and when the black hole evaporates the gravity itself absorbs that information ?
That would not violate the law at all, it just returned to gravity itself so it was not destroyed or created.
If the information in the black hole is leaking out, and it is losing mass, what is the violation since the information would still be there just diffused into the rest of space? Similar to a water droplet evaporating or stars losing their mass over time. I am not getting why the information loss is different in a black hole system versus another system other than the perception that the information isn’t “supposed” so get out.
Could you please update the article to include the recently published Hawking paper titled “Soft hair on black hole” for general reader. I’d like to know what’s new about it?
Maybe the information is sent through to the other side…i theory that at the other end of a black hole would be a white hole and the info (since it can’t be lost or copied) would simple come out the other end…complete but possibly scrambled(?)…and since “the big bang” is theorized to come from a singularity…then could it be possible for how the universe was created, to come from a white hole???
The probability of retrieving the information from reversing a Quantum event is One.
The probability of retrieving the information from reversing a Black Hole event is infinitely small.
The information falling into a Black Hole is not lost and is there but I would not make a bet that I could retrieve it.
Black holes of substantial mass do not evaporate they are merely messy eaters.
There are observational and theoretical reasons to doubt that black holes possess event horizons:
http://www.ptep-online.com/index_files/2015/PP-43-06.PDF
Are there any thoughts on Hawking radiation and black hole evaporation associated with dark matter expansion? Any theories as to why there is so much dark matter surrounding galaxies? Probably asking more questions than we have equations to explain with dark matter… But I do wonder about the relationship between regular matter and dark matter.
Very well done – this is a great resource for a non-physicist trying to get to grips with issues. Thank You!
tgopalan2015 | August 31, 2015 at 4:09 AM | Reply
I was wondering the same thing.
When was this posted???
I don’t see many comments here, it means you have low visitors. I know how to make your site go viral. If you want to know just search in google for:
Kelashy’s method to go viral
If the universe we live in today arose
From the Big Bang of of a black hole
Can’t we say that all the information
Describing our universe existed
In the original black hole?
L.Gopalan
Scott’s observation seem to hold some keys meriting closer examination—Every BH maintains an event horizon and displays Hawkings radition spending energy- Is it in the Master Prograame as in 96 percent waste human jeans that what is given out as radiation is a small portion of non-codified / non- information carrying entities and that there is no loss of info? Also when a new celestial body is captured does the the raditional level increases ?-iam also inclined to agree withy PB | February 16, 2015 at 6:15 PM that tunneling preserves info
I wonder why the idea of hawking radiation as a tunneling process proposed by Parikh and Wilczek is not considered a solution to information loss paradox? Quantum tunneling preserves information.
Hello Dr. Strassler –thanks from another reader on a really astonishingly useful resource; for the non-professional who wants to stay abreast of particle physics I don’t think there is anything else out there to compare with your blog.
Just wanted to add a +1 on the idea of you doing something on Hawking radiation –as I dig more into the topic (just now trying to understand Unruh radiation) I realize it’s something that attaches in a very deep way to some very fundamental aspects of GR and QFT and I would love to read a take on the subject from you as you seem to grasp the problem of pedagogy on physics for non-pros very well.
Matt, sorry about the videos filling the page, I didn’t think they would do that, please delete as they are annoyingly
large (I was not trying for self-promotion here but rather just including the references)…thanks…Emil
Matt,
Up above you stated that:
“It *is* like Zeno’s paradox, in a way; Zeno’s mistake is that he’s right that one can always divide the remaining distance in half, but forgets that one also must divide the remaining *time* in half, with the effect that the total time required to cross the total distance is finite.”
I have just completed three videos which present my explanation of Zeno’s Paradox.
https://www.youtube.com/watch?v=BQZ8P7Uvduo
https://www.youtube.com/watch?v=QhhrlrA85HY
https://www.youtube.com/watch?v=J8KIA_2ARa8
The gist of my explanation was that all Zeno was doing was assuming a mathematical structure of space based on the concept of infinite recursion. Worded differently, he was assuming the existence of a path through space defined by an algorithm employing some form of infinite recursion (typically halving). My conclusion was that this type of structure, if it exists anywhere in the universe, would likely only exist near singularities or at the boundary of the universe. So Zeno’s paradox may be fact near a singularity but it surely results in paradoxical results when applied to normal, “average”, regions of space. The reason for this is that while there is no smallest interval, a recursive algorithm guarantees that the structure of space WILL converge to an infinitesimal point in space where it is not possible to consider any further smaller intervals of movement (within the singularity) because these intervals
no longer have the property of being finite. While it is possible to traverse the singularity in one infinitesimal step it
is not possible to “move” to the center of the singularity because motion ceased at the perimeter. Just as infinitesimals
must a have a property of being finite and non-zero the singularity must likewise have the property of having a non-zero volume.
You stated that Zeno is right that one can always divide the remaining distance in half…My argument is that you cannot continue the recursion once you reach the boundary defined by the infinitesimal volume
of the singularity because this is the point at which you have to start considering the mathematical structure of an infinitesimal and the notion of something “smaller” than an infinitesimal. So in a sense, Zeno was correct that singularities represent the infinitesimal point in space where motion is not possible…does this mesh with what you are saying above?
Kind Regards,
Emil Barbeito
How can all the information end up getting projected onto the surface AND fall into black hole, that would be violation of conservation of energy surely?!
If a black hole has 3 spacial dimensions, once inside the event horizon, can there ever be a 2 way interaction between “particles, energy”, anything really? because any information away from the centre of gravity would be impossible without superluminal speeds..
Is a black hole is just a 2 dimensional sheet, with nothing in the conventional “centre”?
Black holes don’t exist — http://phys.org/news/2014-09-black-holes.html
I am not anything of a scientist, just reading and trying to get some understanding. Is a black hole not something that can be seen as the opposite of the big bang were a singularity (one dimension) became four dimensional spacetime. A black hole is the the opposite? Four dimensional space time turning into a one dimensional singularity. So time is lost as I understand as a dimension at the event horizon but also one of the space dimensions if you describe the event horizon as two dimensional. Why would the interior, if there is an interior of the black hole be three dimensional???
Professor Strassler, I happen to be a relative of Terry Ambiel. I am twelve years old, and I would like to know the difference between a singularity and a black hole.
rofessor Strassler,
Any one on this blog,
In the future is it possible to address stimulated emission proposed by Prof. Chris Adami, from Michigan State University, having to do with the Information paradox.
Thank you for everything you do.
Terry
@elm:
We all know that in math as well as in all factic sciences (sciences completely and exclusively defined in mathematical terms), the meaning of the sign of a value is relative to the origin of the system of coordinates, which means that it is relative to where the zero value is within that reference system.
Because of this fact, we can clearly demonstrate that the sign in itself of any given value could not have an absolute meaning, since its very meaning and existence is relative to some other definition (where the zero value lies within the same system of coordinates).
We know that all it takes is a linear transformation, like a translation, applied to the system of coordinates to change the values (and the sign of the values of many points) within the transformed system of coordinates.
Unless we relate all this math mumbo jumbo to physical concepts, it stays abstract and does not say much beyond math itself.
Let’s consider a physical system of material particles within a conservative field, like say, a gravitational field, in the absence of any dissipation fields (there are no dissipation forces, like friction).
Within such systems, in classical non relatitivistic mechanics, we know that both energy and momentum are conserved. It turns out that, if we analyze this with more detail with the use of Noether’s theorems, we will find that these conservation laws are deeply intertwined with the fact that the behaviour of such systems are not dependent on time (for the conservation of energy) or space (for the conservation of momentum).
That means that we can apply a linear transformation, a translation of time of the form t’ = t + delta_t, or a translation of space of the form x’ = x + delta_x and the corresponding physical quantities will be conserved.
Here we have two translations, one on time and another on space, and we can see that even with these transformations applied, where values of time coordinates (as well as the signs of many points), or values of space coordinates (as well as the signs of many points) can change and that does not affect either the value of energy of the system or the value of momentum of the system.
So, now we have found a physical meaning to this math mumbo jumbo, but we still could argue with G. H. Hardy that the only thing that matters is pure mathematics, while the description of the real wolrd is just a natural “residue” of his principle.
(I’m not an expert on either pure math nor on classical mechanics, so, I apologize in advance for any inaccuracies that I may have included in this description, even though I did my best to validate and review my own text.)
Kind regards, GEN
Hello Prof. Strassler, I’ve got to say that I’m thoroughly enjoying your blog. I came across it while looking for ideas on how to present the concept of virtual particles at an undergrad level in ways that don’t give rise to as many questions as they answer. (It’s still surprising how essentially simple suggestions such as substituting counterintuitive terms like “virtual particle” for “disturbances” can be immediately rewarding!). Along that vein, I was wondering if you’d care to comment on a way I’ve taken to presenting the issue. It’s that the wrong, but typical, response to point (3) above caught my attention, because it’s the reflexive response to the problem when the result is presented as “the black hole therefore absorbs the negative energy from the infalling particle.” Somewhat like the commenter above demonstrates, the question that immediately gets thrown back goes something like “but wait, wouldn’t it be as likely for the other particle to fall in then and add to the black hole’s mass?” At which point I say something like, “well no, even if you switch the particles it doesn’t matter which of the two falls in, whichever it is carries in negative energy and shrinks the BH’s mass.” Which leads to more questions and the temptation to request to just, you know, do the calculation. But that approach doesn’t usually leave anyone satisfied.
Of late, the way I’ve tended to resolve the issue is to present the creation of the virtual particle pair (pardon my language I mean disturbances of course :), at the horizon as borrowing from the energy content of the vacuum for BOTH particles. While the particles are in the vicinity of the horizon nothing special occurs as their own mass/energy content is equal to the one borrowed from the spacetime there. It’s only under the special circumstances, when one of the particles gets away (either one!), that the BH gets to RECOVER only 50% of the mass/energy balance that went into their creation.
Now, this way of presenting things has tended to give rise to fewer questions, and I don’t think I’m mangling what’s implied by the underlying calculation, but I was wondering if I could have your take on it?
“Hawking Radiation”: Do Black Holes Really “Evaporate”?
In 1975, Stephen Hawking published a much cited paper (#14 on the 2012 “All Time Most Cited” list) titled “Particle Creation by Black Holes” [get your copy here: http://projecteuclid.org/euclid.cmp/1103899181%5D, wherein the author claims that:
“… it is shown that quantum mechanical effects cause black holes to create and emit particles as if they were hot bodies with temperature ћk/2πk ≈ 10^-6 (M⊙/M)°K where k is the surface gravity of the black hole. This thermal emission leads to a slow decrease in the mass of the black hole and to its eventual disappearance” [I don’t understand the ћk/2πk reference, and it is nowhere in Hawkins’ paper explained]
M⊙ is the mass of our sun, and M the mass of the black hole. Plugging in a “stellar black hole” mass of ~10M⊙, we get a temperature of 100 nK… (0.0000001 K), that is cold! One view of the Heisenberg Uncertainty Principle shows a relation between the energy E of a particle (pair) and its life time t. For virtual particles, it states ΔEΔt ≤ h/2π (“h-bar”), where h is Planck’s constant. In theory, this is taken to mean that for extremely short durations — Δt on the order of a few Planck times — the First Law of Thermodynamics (energy conservation) may be violated, allowing “random fluctuations” to create virtual particle-antiparticle pairs, on the condition that the pair mutually annihilates before long. In the subatomic “space-time turbulence” called the “quantum foam,” at extremely short distances — a few Planck lengths — this always goes on, everywhere… Including in and around black holes.
Hawking’s paper is rather technical, but to the best of my understanding, what he proposes is:
The enormous gravity at and just outside the hole’s event horizon (somehow) promotes (“boosts”) the creation of virtual particle-antiparticle pairs in the local “quantum foam.” Normally — according to theory — such pairs very quickly mutually annihilate, but due to the hole’s enormous gravitational tug, one or the other member of the pair may slip across the horizon — disappears in the deep — leaving the second member of the pair “escaping to infinity” (radiating away, now as a REAL particle (!), even though neither member of the pair was “real” to begin with. Physics is full of mysteries.).
I have a few questions regarding all this (some but not all of which may be due to my complete lack of understanding of quantum theory):
(1) Thermal emission (electromagnetic radiation) is usually produced by atomic charge acceleration and/or dipole oscillations due to inter-atomic perturbations, resulting in atomic kinetic energy changes. This does not appear to happen in the black hole case. It is not clear (to me) what turns the “escaping” real particle/antiparticle into thermal emission. Help would be much appreciated.
(2) The Second Law of Thermodynamics states that heat always (only) flows from hotter to colder areas. The “temperature of empty space” is ~ 2.73 K (the CMBR temperature), the Hawking temperature of a ~10M⊙ stellar black hole is ~ 100 nK (seven (7) orders of magnitude LOWER than the CMBR temperature), so this radiation would appear to severely violate the second law. Surely, a black hole absorbs far more CMBR than the heat it MIGHT radiate using Hawking’s hypothetical “evaporation” pathway (Hawking admits this in his paper: “… black holes [size ≥ 1 M⊙] would be absorbing radiation faster than they emitted it and would be increasing in mass.” (page 201), and goes on, SPECULATING that “there might also be much smaller black holes which were formed by density fluctuations in the early universe. These small black holes, being at a higher temperature, would radiate more than they absorbed. They would therefore presumably decrease in mass.”)
(3) Negative energy is an idea generally considered speculative today, 38 years after Hawking’s paper was published [Wikipedia: “Virtually every modern physicist suspects that antimatter has positive mass and should be affected by gravity just like normal matter, although it is thought that this view has not yet been conclusively empirically observed”]. But even if we allow the existence of negative mass (and ASSUME that the process deciding which member of the pair that gets “captured” has no preference for antimatter over matter): What physical process would make a black hole lose mass by absorbing a virtual particle pair member? As Matt also points out, with a 50/50 virtual +/– mass contribution the net gain/loss OUGHT to be zero.
As I understand what Hawking’s reasoning boils down to, I can see three distinct cases:
(1) Creation/annihilation inside the event horizon — Wholly “unknowable” process, but since it took place internally, M ought to be unchanged.
(2) Creation/annihilation outside the event horizon. Since nothing was captured by the hole, M ought to be unchanged.
(3) Creation outside the event horizon: one member of the pair escapes, the other is dragged across the event horizon and disappears down the hole: M ought to increase.
Only in case (3) would a net change in M result, but since the origin of the captured mass was the “quantum foam” outside the black hole proper, I fail to see how M could DECREASE as a result. This would imply that the captured “new” (and now real) particle has negative mass, and as far as I can find, particles and antiparticles have opposite charge, but are both supposed to have positive mass.
In his 2003 paper “Do Black Holes Radiate?” [http://arxiv.org/abs/gr-qc/0304042] Adam D. Helfer presents an EXCELLENT discussion of some of the problems with Hawkins’ famous paper, concluding that “no compelling theoretical case for or against radiation by black holes is likely to be made.” Still, this never observed radiation is presented as an ESTABLISHED FACT in many different (and reputable) scientific texts (search on “Hawking Radiation,” and you’ll get the picture). Go figure!
I did some black hole numerical doodling in Excel, using expressions commonly seen in cosmology papers and ditto websites. The extremely wide spread of the “expert opinions” may surprise some of you. For a copy of the spreadsheet, feel free to download it from https://app.box.com/s/iig3s0mxl9jl5ibbts6g.
The more I read about black holes, the more I get a feeling that — somewhere along the line — thermodynamic entropy somehow got confused with Shannon entropy (information theory (two WILDLY different “entropies”)), and that this confusion has lead to the production of a whole lot of equally confused papers…
I highly recommend Helfer’s paper to y’all. Read it, it might clear up a whole lot of this black hole BS (belief system ;)!
I highly recommend against the Helfer paper; I think you will waste your time and confuse yourself about basic issues if you rely upon it. Spreadsheeting will unfortunately not help you understand who is wise and who is foolish; not all opinions are created equal.
As for your questions… they are too many for me to address entirely. It would be helpful if you would try to keep comments a bit more focused, it helps the discussion.
> (1) Thermal emission (electromagnetic radiation)
Thermal emission is not electromagnetic radiation; it is radiation of anything that can be radiated, including neutrinos, electrons, gravitons, … anything lightweight compared with the temperature.
> is usually produced by atomic charge acceleration and/or dipole oscillations
but the mechanism here is completely different and will be explained in a future post. You’re worrying about something that has nothing to do with the physics of Hawking radiation.
> (2) The Second Law of Thermodynamics states that heat always (only) flows from hotter to colder areas. The “temperature of empty space” is ~ 2.73 K (the CMBR temperature), the Hawking temperature of a ~10M⊙ stellar black hole is ~ 100 nK (seven (7) orders of magnitude LOWER than the CMBR temperature), so this radiation would appear to severely violate the second law.
No, it does not violate the second law; you’ve misunderstood what Hawking said. However, you are certainly correct that a large black hole in our own universe would absorb more radiation from the cosmic microwave background than it would radiate in Hawking radiation. Nevertheless, as I have emphasized in my posts, the whole discussion here has **nothing** to do with astrophysical-size black holes. It has to do with a matter of principle, and small black holes are of interest in this matter of principle. So you’re missing the point here. The fact remains that small-enough black holes (some of which may well have formed in our universe, or could someday be formed in experiments or rare astrophysical events) would explode (and did so long ago, if they formed) and destroy the integrity of quantum theory if they don’t restore the information that they absorbed.
(3) Negative energy is an idea generally considered speculative today, 38 years after Hawking’s paper was published
That’s completely wrong: negative energy is the key to understanding why there is anything interesting in the cosmos. http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/the-energy-that-holds-things-together/ The earth is bound to the sun by negative gravitational energy (i.e. the negative potential energy associated with attractive forces.)
[Wikipedia: “Virtually every modern physicist suspects that antimatter has positive mass and should be affected by gravity just like normal matter, although it is thought that this view has not yet been conclusively empirically observed”].
Who said that negative energy has anything to do with anti-particles? It is a completely unrelated issue.
>But even if we allow the existence of negative mass (and ASSUME that the process deciding which member of the pair that gets “captured” has no preference for antimatter over matter): What physical process would make a black hole lose mass by absorbing a virtual particle pair member? As Matt also points out, with a 50/50 virtual +/– mass contribution the net gain/loss OUGHT to be zero.
You’ve misunderstood what I wrote, and you’ve made a bad logical error here. I said that the number of particles and antiparticles absorbed is 50/50. Every one of those particles and antiparticles contributes negative energy to the black hole, as a result of the strong effects of the gravity in which it is produced. So the energy absorbed by the black hole is not 50/50 +/- ; it is 0/100 +/- . [Actually, this isn’t really true either, but that requires a much longer discussion. Really what’s happening is more like 49.999/50.001; because in addition to the Hawking radiation, many other particles that are emitted are absorbed before escaping from the vicinity of the black hole. Stay tuned for an article about Hawking radiation.]
Then you wrote:
—-As I understand what Hawking’s reasoning boils down to, I can see three distinct cases:
(1) Creation/annihilation inside the event horizon — Wholly “unknowable” process, but since it took place internally, M ought to be unchanged.
(2) Creation/annihilation outside the event horizon. Since nothing was captured by the hole, M ought to be unchanged.
(3) Creation outside the event horizon: one member of the pair escapes, the other is dragged across the event horizon and disappears down the hole: M ought to increase.
—-
(1) correct.
(2) correct.
(3) wrong. Why do you think Hawking is famous? Because he proved that the energy of the absorbed particle is negative and the black hole mass decreases. Think of it this way: a Hawking particle is emitted. That particle goes off to infinity, far from the black hole: its energy is obviously positive. How was energy conserved?! Did energy just come from nowhere?
Hmmm??
It was conserved because the energy of the absorbed particle was negative.
As for the relationship between different types of information — this *is* potentially confusing. But the confusions have been hashed out, and your suspicion isn’t right. The problem is deeper.
@Oaktree:
When it comes to Physics, It is not proper to say that causality implies purpose.
If we consider the definitions of the word “purpose” given by the Merriam Webster Dictionary, it says:
“:the reason why something is done or used : the aim or intention of something”
: the feeling of being determined to do or achieve something.”
: “the aim or goal of a person : what a person is trying to do, become, etc.”
All three definitions of purpose clearly relate to “the will and intention of an intelligent agent to obtain a given result”, clearly these definitions do not apply to what means causality in Physics.
Besides, strict causality does not apply to quantum field theories.
Small black holes evaporate fast, while massive black holes evaporate in a rather slow fashion.
There is a theory of classical black holes, and there are many (with its variations) quantum theories of black holes.
It is my understanding that the paradox arises with the quantum theories of black holes, and not with the classical black hole theory.
Regarding the negative energy that is being swallowed by black holes, that comes from anti-particles, right?
It is when anti-particles of the pairs formed around the event horizon are swallowed by the black hole, and since anti-matter has negative energy, it substracts from the positive energy of matter (a given anti-particle could only substract from its corresponding particle, right?) within the black hole, and over a long period of time, black holes will evaporate.
Correct, the problem comes from the quantum theory of fields in the presence of quasi-classical black holes.
The negative energy does not come from anti-particles, at least not in the sense you mean it. Specifically, it’s not true that particles have positive and energy and anti-particles have negative energy. For instance, a black hole could emit an electron and swallow a positron; but it could just as well emit a positron and swallow an electron. Or it could emit one photon and swallow a second photon. It’s also possible for a black hole to emit a photon and absorb an electron-positron pair, or vice versa.
So I’m afraid your last paragraph is completely wrong. Anti-matter has positive energy, under normal circumstances, just like matter. You can guess this from the fact that photons are their own anti-particles (as are several other types of particles) — how could photons both have positive and negative energy? No: the point is that the effect of the strong gravity near the black hole can be to cause particles’ (and their antiparticles’) energy to go negative.
To Matt Strassler: You said “..the effect of the strong gravity near the black hole can be to cause particles’ (and their antiparticles’) energy to go negative.” -> Hawking also said this in his book but I still do not understand why/how this is possible. How can “(strong) gravity” near a massive object cause particles to have “negative(?)” energy? The gravitational potential energy of a particle with “positive energy (or positive mass)” decreases as it approaches a massive object (or black hole) but its energy stays positive all the time, right? When/how (or at what point? or under what condition?) can it start possessing negative energy? sounds impossible. If the particle’s potential energy by gravity is set as 0 at infinitely far then its potential energy seems to always stay negative at least mathematically but it is just a matter of a reference point. and does not mean the particle’s energy goes negative or it has negative energy. Is this not the case? Anyway, could you explain how a particle’s energy goes “negative” under strong gravitational influence (or near the black hole)?
@elm, in classical mechanics, central potentials like the gravitational potential act on bodies with mass with a negative value of potential energy, while other kinds of energy, like kinetic energy, have a positive value.
Because potential energy of the gravitational field is negative, all bodies with mass close to the gravitational field are captured by this field, unless the bodies have enough kinetic energy to counter the negative energy.
The speed associated with the “break even” value of kinetic energy necessary to counter (to compensate for) the negative potential energy is apty called the escape velocity.
This is the speed required for a rocket to escape the gravitational hold of the Earth and move beyond an orbit around the Earth, like for instance, to go to the Moon, or Mars.
Kind regards, GEN
@Gastón E. Nusimovich (and later part to Matt Strassler), thanks for your comment but I am already aware of this. and that does not answer the mechanism or my question. it just re-describes or re-states partly what I already said and what happens at our currently accessible/observable scale or numerically. Abstract numerical or mathematical relation is useful but not a satisfactory explanation without physical model. Can “energy” go ever “negative” not just mathematically/numerically” but also “”physically””? If so, how/why? stuff like the following is far from satisfactory ->Hey, you just count energy numerically and oh it turns out that you can consider it to go negative because it requires energy to pull things apart under gravitational influence. The total energy (potential and kinetic) of the system is always “positive,” is this not the case? Can the total energy of the system ever become negative?? if so how(physically)? If gravity or any potential energy can take negative value “physically”, how is this possible “mechanistically” (=at the most fundamental level or microscopically?)? I am not sure if negative kinetic energy can physically exist but I cannot think of such a thing (it seems impossible/absurd intuitively and empirically). What about negative potential energy? Can it exist physically? if so how? There must be “physical mechanism” for any phenomenon to happen because nature (=physical phenomena) does not care about nor follow goddamn numerical laws (it is for humans to grasp and sort out things) but because its building constituents (whatever it might be) have certain structures/mechanisms, nature seems to follow rules/laws. If string theory or something more fundamental can explain this from “the fundamental constituent”, it sounds very satisfactory and interesting. I hope Matt Strassler or someone can add another (or a few more) deeper layer/angle/facet of explanation/model to this phenomenon (with the latest more satisfactory development? in Physics).
“Maybe the information came back out with the Hawking radiation? The problem is that the information in the black hole can’t get out.”
Information can’t get out because it can’t get out? Could you explain?
And for conservation of mass/energy to hold, wouldn’t all matter within the evaporating black hole have to be converted into Hawking radiation as per E = mc^2? If so, it seems logical to me that information would follow the matter through this conversion and escape with the radiation.
In general relativity, once anything crosses the horizon it can’t come out. That includes information. Hawking radiation isn’t about something coming back out of the hole; it originates right at the horizon, not inside the hole… so, at least naively, it can’t possibly carry the information back out.
The only way around this is to modify general relativity somehow… which seems quite plausible, since we know at least one modification (namely, string theory). But no one has shown even how string theory solves the problem, so it just isn’t clear what’s the right way to understand what’s going on.
What seems “logical” to you IS logical, I agree. However, it’s wrong, because that’s not what’s happening. Matter falling into the black hole isn’t converted into Hawking radiation via E=mc^2. All of that matter remains in the black hole.
Instead, in Hawking’s calculation, quantum fluctuations of quantum fields at the horizon produce a disturbance which has positive energy in one region and negative energy in another. Sometimes, the positive energy disturbances leave the area, as Hawking radiation, and the negative energy disturbances fall into the black hole, reducing its mass. Yes, that’s weird. But correct. And these fluctuations are simply those of quantum fields in empty space, containing (apparently) no information at all.
This is a case where the devil is definitely in the details. It’s not an accident that the world’s most experienced and insightful physicists have been confused about this for 40 years. There’s not going to be an easy, simple-logical way out.
hmm… from the above 3 paragraphs: 1) “All of that matter [that falls in] remains in the black hole.” But it must go somewhere if the black hole shrinks…
2) “these fluctuations [Hawking radiation]… containing (apparently) no information at all.” But a Hawking photon can be observed, so would count as information, yes?
“Instead, in Hawking’s calculation, quantum fluctuations of quantum fields at the horizon produce a disturbance which has positive energy in one region and negative energy in another. Sometimes, the positive energy disturbances leave the area, as Hawking radiation, and the negative energy disturbances fall into the black hole, reducing its mass. Yes, that’s weird. But correct. And these fluctuations are simply those of quantum fields in empty space, containing (apparently) no information at all.”
The gravitational field, as we know has a negative energy in the sense that it must consume energy to get away from it.
Ιf in the black hole falls “negative energy” from the quantum vacuum, because that does not mean increasing the mass of the black hole and not reduce this.
I wonder if exist a clear mathematical solution for this problem.
So by following the above sense if in the black hole dropped positive energy from the quantum vacuum would have increased mass, and the event horizon of the black hole;
Of course there is a possibility of three will say: All negative and positive energy that falls into Black Hole to be + n, -n ie zero, at some time of observation, so should the horizon oscillate.
Gibbs’ theoretical developments on statistical thermodynamics are very important for chemistry, both for theoretical chemistry and for experimental and industrial chemistry.
One of the most important theoretical developments of Gibbs, from the point of view of chemistry, is his theory of Free Energy.
This physical magnitude, Gibbs’ Free Energy, is very important to determine if a chemical reaction is thermodynamically feasible or not under a given set of (thermodynamical) conditions.
In chemical engineering, that deals with the design of factories to produce a given chemical product or products, you have to do a lot of theoretical work at the start of the design, and you use many different sets of equations, in an iterative process, to get to the bottom of a good design.
You may also do computer simulations, also in an iterative process, until you have a fairly good design for a pilot plant. This pilot plant could be either real or a simulation, but this is major step in the long process that would get you to a proper design for a real plant, a complete factory capable of producing a certain chemical product or products with economic efficiency.
The production of a given chemical product always produces other by-products, so, your design has to deal with those by-products too, from many perspectives, including economics and the protection of the environment.
Kind regards, GEN
Those “cells” belong to a classical mechanics deduction of the equation for Entropy, so, they could be used as a description of Entropy for certain types of phenomena, mainly classical.
But that definition has limitations, in fact, Josiah Willard Gibbs Jr., a major contributor of this theory, clearly understood these limitations, which he exemplified with a famous paradox, which required a quantum mechanical approach to be solved.
Two of the 1905 papers of Einstein make a good use of statistical mechanics. Later, when Einstein found out about Gibbs’ papers of this subject, he commented that if he knew about Gibbs’ work back in 1905, he would not have wasted time with the simple stuff he did.
Questions to GEN.
Are these space “cells” eaten by a black hole?
Is entropy decrease by pair e-e+ production out of the nothingness of the vacuum at the BH horizon possible?
The history of Physics and of Science in general tells us that when these paradoxes or incosistencies appear, it means that we have bumped into a path towards a breakthrough, an unexpected discovery path towards new theories.
Let’s consider a couple of examples. The so-called Ultraviolet Catastrophe, or the Rayleigh–Jeans Catastrophe, is what led Max Planck to desesperately find the right equation that would correctly explain Blackbody Radiation, and at doing so, he let the Genie of Quantum Mechanics out of the bottle.
Another example. Around the mid 1860s, Rudolf Clausius published a paper where he introduced the concept and first formal definition of Entropy.
A few years later, Maxwell and then Boltzmann expanded the branch of statistical mechanics to develop a new branch of physics called statistical thermodynamics.
They used this new branch to develop a theory that could predict the values of thermodynamical properties for ideal gases.
One of the properties that proved very difficult to model with this theory was Entropy.
The first problem that showed up was rather thorny: we knew by then that Entropy, using Clausius’ definition, has a finite value.
Statistical Thermodynamics uses continuous variables for these models (it uses a particular kind of formal space known as phase space). But if we try to define Entropy this way (with continuous variables), we get an infinite value, which cannot be.
So, a mathematical trick was used as a workaround to overcome this issue: to use a discrete phase space with a particular definition of “cell” size so the calculations could give predictions more consistent with experimental measurements.
This trick did overcome the first hurdle, but there were other bumps down the road. The second issue what that if we considered molecules or atoms distinguishable from each other (that was the “right” way of thinking at the time), the predictions were wrong, but if we considered them indistinguishable from each other, the predictions were more in line with the experimental measurements.
At the time, scientists were content with the fact that they could have a mechanical model of the statistical behaviour of billions of molecules of (ideal) gas and be able to predict the values of thermodynamical properties of the gas, even though they did not realize the major significance of these “tricks” that were used.
The trick of having a discrete space made out of “cells” of a particular size was actually a precursor of quantum mechanics, as the particular “size” of the “cell” is turned out to be Planck’s constant.
The fact that we need to use a discrete definition of phase space for this model to ever work is a precursor of the Uncertainty Principle.
The fact that we need to consider molecules to be indistinguishable is a precursor of what Bose bumped into and it later became a major tenet of quantum mechanics.
The case in point is that at the time these tricks were considered, not much attention was given to the physical signififcance and meaning of these mathematical “gimmicks”.
Kind regards, GEN
How would the theory change if Fermions would be repelled from the black hole, if fermions are assumed to be Calabi Yau shaped spinning propeller objects able to polarize at one of the two ore even three BH horizons against the infalling vacuum?
There’s one thing we could all agree, no matter what side we take regarding the firewall paradox:
Stephen Hawking still maintains his uncanny ability to grab the center stage with witty and flashy comments.
No wonder Leonard Susskind calls him “The Evel Knievel of physics”, not only because of his antics, but because he seems to be willing to suffer a fall every now and then.
Matt,
When you refer to “flat space”, you mean space-time where all 4 dimensions are flat, they have no curvature?
All four… flat space-time. Thanks for the question, I should have said that, and in fact I’ll revise the comment to make that clear.
It is very clear that with this type of problems, having enough complexity, you need to work with the equations to get any useful and theoretically valid insights.
Kind regards, GEN
Matt,
Thanks a lot for the explanation about Unruh radiation and accelerated observers approaching a black hole.
Could you please give some details on why any observer on an inertial reference frame (either stationary or moving with a constant speed vector) would not detect Hawking radiation?
I will have to write an article on Hawking radiation, and at that point I will explain it. But it’s not something I can do in a comment.
Also, be careful: don’t mix the notion of ” inertial reference frame (either stationary or moving with a constant speed vector)”, appropriate to flat space-time, with “Hawking radiation”. Hawking radiation applies with black holes; it’s not the same as Unruh radiation, which is a more general thing that applies even in flat space-time. You notice I used the word “seed”. Hawking radiation is a sort of little low-energy tail of Unruh radiation which makes black hole horizons different from flat-space-time accelerating-observer horizons. So to understand Hawking radiation, you should first understand Unruh radiation in flat space-time, and then understand how the region near a black hole (the “Rindler region”) differs very slightly from flat space-time.
@JollyJoker,
There can’t be instant communication without breaking the speed limit of C.
It has been proven that not even quantum entanglement breaks this condition: our universe does not allow to send communications faster than the speed of light.
I think JollyJoker’s question is really a simpler one… see above.
Thanks a lot for this, Matt. My 12-year-old wanted to know what Hawking had said, and I knew I could count on you for a clear layman’s explanation. Now I’ve just got to translate this again for him. 🙂
Glad to be of service, Brad! Translation often has to proceed in two steps… let me know how you approach it. Someday I have to write an even less technical introduction, but wow! not easy!
Thanks for the article, Matt – I found it very helpful.
Some basic questions:
(i) is energy conserved when a black hole evaporates?
(ii) You use the phrase “information is never truly lost, nor is it truly copied”
Is information ever created? Or is there a fixed, constant amount of information in the universe?
If the latter, is there a law of conservation of information? (It is not a phrase which seems to get used in this context)
(iii) If there is a law of conservation of information, is it of a type to which Noether’s theorem applies? If so, what is the corresponding symmetry?
@Duffieldjohn:
Before the following picture was taken, in 1989, we had no real and complete evidence that atoms existed.
http://en.wikipedia.org/wiki/File:IBM_in_atoms.gif
That posture, that we have to discard a theory or a concept because there is no direct and incontrovertible evidence, is basically the Mach Principle.
In fact, Mach himself was against the idea of atoms, because he argued (using his own principle), that we would never be able to detect atoms.
At the time of his argument (late XIX century and beginning of the XX century), Mach was a very well respected physicist and his views and ideas gathered a lot of force and respect from his peers.
On the contrary, Ludwig Boltzmann was a strong believer and supporter of the idea of atoms, and he was convinced of their existence mostly due to his own research on Statistical Thermodynamics.
They clearly established a bitter and harsh dispute over the validity of the atomic theory.
It was Einstein’s 1905 paper on Brownian motion that started to turn the tide in favor of the acceptance of the atomic theory.
Any chance that the uncertainty principle and information leakage from a black hole might be related?
Such as, information leakage out of our black hole is the origin of our imperfect knowlege of momentum and position, etc?
The uncertainty principle and the black hole information problem are indeed intricately related. But information leakage out of black holes isn’t going to introduce or create uncertainty of the sort that stabilizes atoms and sets their size. Nor does quantum uncertainty about the location of the horizon (i.e. edge) of a black hole, which certainly is an issue people think about, seem to help resolve the black hole information problem.
Just a point of clarification re. terminology for non-experts:
As is often the case, linguistically challenged theoretical physicists seem to have no idea what the words they use actually mean. To wit, the dictionary definition of “firewall” is “a wall built to stop the spread of fire” — i.e., a wall through which a fire cannot pass. In computer networks, a “firewall” is a device that helps to isolate a local network or sub-network from the potential threats and chaos going on in a network outside of the firewall. Theoretical physicists have taken the term and turned its meaning around 180 degrees: to such a physicist, a “firewall” _is_ the fire — i.e., a “wall of fire”, sitting outside of a boundary (which is what probably really should be called the “firewall”). To anyone familiar with its actual meaning, the use of this term here could make the explanations even more confusing. Just FYI…
Thanks! Though actually, the clever thing about the term “firewall” is that it really has BOTH meanings in this context — it locks everyone out of the interior of the black hole [essentially making the interior not exist at all], and does so by means of a wall of “fire” (really, a bath of very high-energy particles, so more like nuclear “fire” than chemical fire.)
The energy density of Hawking radiation depends on the diameter/curvature of particle. When some tiny particle appears in strong gravity field near event horizon of black hole, it will evaporate in the same way, like the black hole of the same diameter. The consequence of this behavior is, if we place a tiny particle into gravity field of black hole at it proximity, it will radiate the Hawking radiation and it will evaporate fast. As the result, the black holes aren’t so opportunistic eaters, as the classical theory considers. Most of matter will evaporate into radiation before it could even reach their event horizont, which does behave like the firewall in this way. Due the radiation most of mass of infilling matter will get spread across interior of event horizon, thus solving the informational paradox.
Matt, among your articles this was one of the most interesting I read. Congratulations.
Some ideas:
1) Is there any chance to obtain observational data from or do experiments with black holes that help to decide what kind of firewall, if any, there is? There are lots of thought experiments about black holes, but any real experiment should help a lot. It is still not possible to create microscopic black holes in a laboraty, is it? And the gigantic black holes in the center of the galaxy are too far away to serve for useful observations at the moment, aren´t they? Could the cosmic radiation hitting the upper atmosphere of Earth produce some tiny black holes that we may observe?
2) Can we expect that the expected modification(s) of the theori(es) related to predict observable effects not only for black holes, but also for other objects?
3) The discussion of the evaporation of a black hole considered an ideal situation that starts with a black hole of given size which then evaporates with time. However, real black holes, such as the big one in the center of a galaxy, absorb incoming matter (and radiation?), so at the same time they lose mass/energy via Hawking radiation and gain mass/energy by absorbtion. Does the new absorbed mass/energy somehow compensate the loss of old mass/energy, in particular with respect to possible loss of information? I wonder whether the absorption of more matter (temporarily) stops the effect that finally may lead to a firewall or not. Also, it is not obvious to me what is “half the size” of a black hole if a real black hole probably starts with a medium size (such as collapsed star) but then grows by more mass/energy falling into it. Is the reference size the original size of the black hole when it first was created?
“And when you have eliminated the impossible, whatever remains, however improbable, must be the truth.”
Well said mr. Duffield. One decent hypothesis is that a BH is just a blob of stuff, just like an electron, but naturally in very much bigger scale. Hypothesis is not QM compatible, but that’s not the end of the world (QM needs also redo).
You can hypothesize all you want; can you please calculate something? Or show that Hawking’s calculation is actually wrong, despite 40 years of checking it in multiple contexts?
Yes Sir! That shouldn’t be a problem for a man who created the TOE. I put your request on top of my todo list.
I suggest you read some of the literature before you plow in unsuspecting…
Unfortunately I have to give up my plans to write the paper. Doing decent work would require too much time, maybe later…
Here you have some feedback:
IMHO you haven’t explained carefully enough why the loss/copy of information is incompatible with quantum physics, which is after all the starting point of the whole issue. At least, I haven’t been able to understand it.
@gongon; There is a fundamental “No Cloning Theorem” in QM which forbids copying a quantum state. Loss is OK. Let us see what Matt says about this.
Let’s bear in mind a few of the rules of QFTs:
The complete state of a given type of particle is determined by a discrete set of integer numbers, so, that means that all we can say or all we can use to describe a particle is its current quantum state, which is completely determined by this given set of integer numbers.
If we have a bunch of particles with the very same quantum state, these particles are indistinguishable from each other, in the sense that you can’t say something like “this is particle A and this is particle B” because there is no way to determine or measure differences between them.
You can have a bunch of bosons with the very same quantum state and “together”, very close to each other.
You can have a bunch of free fermions with the very same quantum state and “together”, very close to each other, but it is not that easy to keep a bunch of bound fermions “together”, very close to each other, even if they have some difference in their quantum state, like say, all but one of the integer numbers (that determine the quantum state) have the same value.
An example of bound fermions is electrons (these are fermions) in atoms, or protons (these are composite fermions, but fermions after all) and neutrons (these are composite fermions) in the nucleus of an atom.
In fact, it requires a lot of pressure to force bound fermions to be close to each other, like say, the pressure caused by the collapse of a large star, at least larger than 1.44 times the mass of our Sun. A star like our Sun, when it runs out of nuclear fuel, collapses due the gravitational pull, but it does not have enough mass to force the bound fermions to get too close to each other: in fact, this resistance of bound fermions to be close to each other is so strong that it does stop the collapse of the star.
It is possible to create a bunch of particles of the same type and with the same quantum state. This is done routinely in particle colliders, which is a necessary condition for many experiments: that you collide a bunch of particles in the very same state.
As already mentioned, we create a bunch of particles of the same type and with the same quantum state, but that is not the same as “copying” particles.
Regarding the prohibition of information loss, this is a condition (or a law) that is predicted by a mathematical theory aptly called Information Theory. This prediction says that all processes used by any information system experience a physical property called entropy.
Any ideal process of the information system will maintain the value of this property entropy after its execution (entropy will not change its value), but any real process with increase the value of entropy.
For an information system to work with information, it has to use processes. This processes transform information from one state (value) to another state. That is why information systems are useful, because of these transformations they can apply to information.
A real information system can only use real processes, which means that the transformations on information done by real information systems always happens with an increase of entropy.
The important aspect here is what this increase of entropy does to the information after each transformation (after each process): the transformation of the information is not “perfect” in the sense that the information that results from the transformation has some “noise”, some “bad” info, some “inpurities” within it.
After a few transformations in any given sequence of processes, the accumulated noise is such, that all you get is “garbage”, or so it seems at first glance.
What the prohibition of information loss says is that, even though it looks like the information is lost, it is not so, the original information is mangled but somehow it is “encoded” within the “noise”.
This theory describes the behaviour of any information system, either real or imaginary. A computer is an example of a real information system.
A computer uses quantum mechanical effects to do its magic, so, we know that information theory applies to quantum mechanical systems. When I say “we know”, I mean that we both have predicted that Information Theory applies to quantum mechanical systems, and we have experimentally validated this prediction under a large amount of scenarios and experimental conditions.
Kind regards, GEN
This explanation deserves a few additional comments:
One of the real values of Information Theory is that we can predict how information gets “garbled” after each real process of any real information system, and use these predictions to design counter-measures to the “garbling” based on including redundant information to the input, to the original information.
This redundant information is used after each transformation to weed out the noise and get the “true” result of the transformation.
This same theory has been very succesful in helping the design of cryptographic systems, useful to encrypt and protect information to be sent over an “untrusted” channel, and to design compression systems, useful to compact large sets of data into smaller sets of data.
I don’t know what you mean by saying “Loss is OK”. Neither loss nor cloning is possible in a quantum theory. Apparent loss is possible if you lose track of the information, but there’s no true loss.
Oh! poor choice of words! What I meant was that quantum state can suffer decoherence although overall unitarity has to be conserved.
Thank you. I agree with you, and plan to write a longer sub-article, to be linked from this one. But I need to get my facts straight first.
@JollyJoker,
When you say “Should an observer in a black hole ever see stuff disappearing?”, the main thing to consider here is the verb “see”, which involves light travelling from “the stuff” to the observer … at the same time that gravity is exerting weird actions on “the stuff”, the passing of time gets slower and slower, due to the intense concentration of energy/momentum (let’s call it mass for the time being), so, the observer will receive images of slower and slower movements of “the stuff”, until “the stuff” seems to stop moving, frozen in time, as long as the observer is not also affected by the weird actions of gravity (stretched like a spaghetti of play-do).
But since the inside of a black hole seems to be very complex, it is my understanding that scientists do not have a very thorough and complete model of what is the behaviour of “stuff” within the black hole, just a brief glimpse of what goes on inside them.
See above; I think your answer is beside the point.
I meant an observer inside the event horizon, but you do bring up another thing that I don’t have a clear picture of. If an observer outside the hole sees the infalling guy (and his clock) move slower until he stops completely and never passes the event horizon; isn’t whatever the infaller experiences inside the hole happening sometime beyond the infinite future when the outside universe has seen the hole evaporate an infinity ago?
There, I solved it! 😉
Thanks to both of you for the explanations!
Of course that intuition underlies complementarity: the fact that the outside observer never really sees the infalling observer enter the black hole, but rather sees him/her redshifted and (according to complementarity) scrambled and spread out over the horizon by quantum effects. However, remember the black hole disappears. So the intuition you’re relying on fails, eventually, because in some way the infalling observer comes back out (scrambled) in a FINITE time. Complementarity was the assertion (without proof but with supporting arguments) that you can run with the intuition you suggested all the way through the evaporation process. The AMPS paper is the statement (based on simple assumptions) that, in fact, you can’t.
“Of course that intuition underlies complementarity”
Of course. I’m just happy you didn’t say “recall that” 😉
Rats, I should have.
Sorry for bothering you with this again, but I’m starting to wonder how an infalling observer can ever enter a black hole even from his own perspective. Shouldn’t he see the stars fade and die just before he hits the horizon AND the horizon burn away in Hawking radiation before he ever touches it? He should fall towards the horizon at the same rate it recedes and end up in empty space in the time just after the BH has finally evaporated, shouldn’t he?
After the infalling observer has entered the black (has passed through the event horizon) but before the observer gets to the singularity, the incredible tidal forces of the black hole will violently stretch the observer like play-do in an instant, for any observer that happens to be taller than zero feet tall.
So, the observer will not last alive a long period of time inside the black hole.
This doesn’t address the question.
I’m probably making some Zeno’s paradox-style mistake, but I don’t see where.
Gaston, I’m talking about before he enters the event horizon. If the time in outside universe moves faster and faster as he approaches the horizon, how can he pass it before it’s gone?
Answered now; see above.
Eh. Apparently the infaller also sees the outside universe slow down (to half speed when he crosses the horizon). Presumably my original view assumed a symmetry that’s not there. And/or instant communication.
Right; the reason there’s no symmetry is that (unlike standard *Special* relativity apparent-paradoxes, where two observers who are traveling at constant velocity relative to one another each think the other’s clock runs slow) in this case the infalling observer is not fighting gravity (or isn’t fighting it that hard) while the outside observer is using a rocket ship (or some other method, like being in orbit) to stay outside.
It *is* like Zeno’s paradox, in a way; Zeno’s mistake is that he’s right that one can always divide the remaining distance in half, but forgets that one also must divide the remaining *time* in half, with the effect that the total time required to cross the total distance is finite.
The outside observer sees the infalling observer slow down as he/she approaches the horizon, and the observer’s clock slows down too. But the infalling observer uses the slower clock, and so does cross the horizon in finite time, from his/her own point of view.
And the infalling observer, while observing some slightly odd effects as s/he enters the region somewhat near the black hole, does not notice anything special while actually crossing the horizon. The stars do not fade and die at that particular point in time and space.
That’s all classical relativity, no quantum theory needed. And so far there’s no clear sign that quantum theory would change this.
Quantum theory combined with relativity then gives us Hawking radiation. The tricky part is that an infalling observer does not see the Hawking radiation at all. Only an outside observer sees it.
This you can prove. The seed of Hawking radiation [Note added: I explain a bit more about what I mean by “seed” in a comment below.] is “Unruh radiation”. The vacuum of simple flat empty space-time, as viewed by a stationary observer (or one moving with constant velocity) is, of course, empty. But the vacuum as viewed by a constantly-accelerating observer is full of particles! That is Unruh radiation. It’s obviously there from the point of view of an accelerating observer; it is obviously absent from the point of view of one who is not accelerating. And the accelerating observer also sees a horizon, almost exactly like a black hole horizon; because information about what is happening behind the horizon can’t catch up with the accelerating observer, so (unless s/he stops accelerating, which s/he can always choose to do) that person will never learn what happened behind the horizon.
The difference between this accelerating-observer horizon and a black hole horizon is small, if the black hole is large, but as the black hole evaporates the difference becomes essential.
Finally: in general the observer can fall toward the horizon much, much faster than the horizon evaporates, unless the black hole is already very small. How fast the observer falls depends on whether s/he has a rocket to slow or speed his/her descent. How fast the black hole evaporates just depends on the size and other properties of the black hole. For a big black hole, in general the observer without a rocket will descend at high speed, while the black hole itself will evaporate very, very, very slowly.
If I’m not mistaken, it was Charles Sanders Peirce one of the first scientists (if not the first) to explain with a theory how important it is to any science to work on a collaborative work of a community of experts, and to use peer reviews to validate theories so as to help science advance and progress.
So, you just can’t get a “one-man” theory, and this is not what Einstein did, because once he was certain about of any of his papers, he published them.
Besides this, a theory is about predictions that can be validated or refuted by experiments, and experiments are all about measurements, so, any credible theory has to present quantitative predictions to be validated or refuted by experiments.
To offer these quantitative predictions, theories must present equations.
Should an observer in a black hole ever see stuff disappearing? I’m not quite clear on why complementarity becomes a problem only after half the hole has evaporated; surely any decrease in its size should make stuff inside the horizon disappear as well? Is this something about time on the inside passing slower than on the outside? Or not at all?
It’s honestly *really* hard to explain without technical apparatus. It’s not at all intuitive, unless you have a lot of experience with quantum entanglement and with how holography works… and as yet I have no idea how to explain it non-technically, which is why I hadn’t tried to write about this subject, until this past week’s Hawking hoopla forced my hand.
The issue has to do with information storage and which objects are quantum-entangled with which other ones. A key step is Don Page’s observation in http://arxiv.org/abs/grqc/9305007 that if you break a quantum system into two parts, the smaller part carries no information about the full system, and all of the information is in the larger part. Talk about non-intuitive! But it’s true.
Thx! Has ‘t Hooft weighed in?
He has, to a degree. All the big names have done so. I really don’t expect the solution to come from the names you know. Remember Hawking was about 30 when he showed black holes radiate.
I can see the source of frustration here. I wonder when physicists eventually give up and start looking for a better theory? It might take a year or centuries… What do you think, Matt?
Oh, I’m sure your own theory solves these problems in a remarkably simple way, doesn’t it… 🙂
Beats me! But I might write a paper about BHs in future 😉
As i understand, X-rays are emitted whenever matter falls into a black hole. Could the X-rays be considered as information about what fell in?
Michel Beekveld
Electrically charged matter would emit X-rays, but, for instance, neutrinos, which are electrically neutral, and photons too, would not. That said, everything emits gravitational radiation, though this is incredibly tiny. I don’t believe this radiation can be used to address the information paradox — it certainly can’t solve it by itself — but I am not entirely confident it can’t play some role in the solution.
Hi Matt. I always value your blog for its carefully nuanced presentation, despite addressing lay audiences. Unfortunately, I think that your description of quantum theory is a bit misleading. In addition to having a reasonable definition of probability, one probably also needs linearity to make the above claims. (For instance, final state QM gives probabilities that sum to one.) Also, if one wants to have purity preserving evolution (ruling out, for instance evolution using the Lindblad equation, which also gives probabilities that sum to one), then one probably wants to appeal to locality and/or energy conservation as Banks-Peskin-Susskind did. (And that doesn’t bring into the discussion some proposed counter-arguments to their claims.)
Thank you for reminding me of these subtleties. Are these reviewed somewhere? I clearly haven’t thought about some of these details for quite a while.
Unfortunately, I don’t know of any good review that covers this particular issue. Most people I think just refer to the Banks-Peskin-Susskind paper. (Most people seem to ignore the counter-arguments raised by Unruh and Wald; I won’t comment on whether this is appropriate or not, except to say I personally don’t find their case for non-unitary evolution compelling. Basically, it seems that once you decide that your putative non-unitary evolution is going to keep track of energy, one essentially ends up with new degrees of freedom and considers unitary evolution in the enlarged hilbert space.) Some of what you want is probably in quantum information sources. I’ve mostly had to assimilate my understanding of the situation from various original sources and some quantum information texts, eg. Nielsen-Chuang. (They will certainly discuss quantum operations and I think the Lindblad equation.) I may as well mention my own (pre-AMPS) paper arXiv:1109.2911v2, since if nothing else the major references are there.
Of course, one can also go back to Hawking’s papers in which he proposes the S matrix should become a dollar sign. Obviously, he had in mind that probabilities would still sum to one, but that information would not be preserved.
I was entirely ignorant of final state QM (and the related Horowitz-Maldacena proposal) until the firewall debate started, for instance. I think Preskill has some posts on his blog (and some papers) about the possible relevance of final state QM to the firewall debate. Bousso discusses it in several of his recent firewall papers, and argues that it doesn’t seem to work.
Perhaps someone else is cognizant of a nice review of the case for unitary evolution?? If I think of/find something I’ll post it here. My apologies if I have misconstrued/omitted anyone’s work.
I was going to leave a comment to similar effect, that consistent probabilities alone don’t imply conservation of information, you need some additional assumptions. Unfortunately, I’ve learned what I know about it much the way Avery has, from some quantum information notes and some papers. Avery, if you find a good review of these topics, I’d like to read it.
The paradox has nothing to do in itself with the holographic principle per se.
The existence of a holographic phenomenom in itself does not give rise to the paradox: the paradox seems to be a consequence of a complex problem with not enough theoretical understanding of all the equations that are relevant to describe how a black hole really behaves.
More precisely; the problem arises in the process of black hole evaporation. A stable black hole in equilibrium with its environment (absorbing energy as fast as it radiates energy) seems to be consistent with holography, but is not a source of a clear paradox.
Is there a similar paradox that occurs in strange metals where the holography idea is being applied? Is there some information to be gleaned from this real world example that might help?
Not that I am aware of. The problem of black hole formation and evaporation is hard to translate into a precise question that you could ask experimentally of a metal, or theoretically of a quantum field theory.
@SomeGuy:
Your description has some conceptual errors:
For instance, when you say “Later on, another photon with information content i2 exits as Hawkins Radiation” …
This is wrong: No particle can exit from the event horizon, no particles could come out of the black hole.
What happens is that a pair of virtual particles spontaneously appear by the event horizon: one of the particles is attracked to the black hole and is swallowed by it, while its pair is left outside of the event horizon, turns into a real particle and can be detected as Hawking radiation.
The information of the particle swallowed is not entirely lost, as its pair that stayed out of the black hole carries that info in a rather mangled way.
“No particle can exit from the event horizon, no particles could come out of the black hole”
That’s not clear, and the lack of clarity is simply because we lack a quantum theory of gravitation.
The produced pair arises out of energy donated from the gravitational field; the outgoing half of the pair carries energy away from the black hole. The (semiclassical) energy-momentum conservation is the key here to determining how much local mass-energy is carried out of the system in the outgoing half’s momentum-energy. The validity of semiclassical gravity outside the horizon — notably with respect to mass distributions with which no problems with semiclassical gravity are expected — is one of the postulates of black hole complementarity about which the firewalls paradox raises questions.
Observations about all causal horizons depend on the observer’s acceleration. A theoretical observer unaccelerated with respect to the black hole and theoretical observers riding along with each half of the pairs produced near the former’s calculation of the location of the event horizon are likely to disagree on where the point of no return is. For a sufficiently massive black hole (where the spacetime curvature at the event horizon is still gentle) the infalling theoretical observer is expected by the equivalence principle to be able to perform local physics experiments with normal results even after all three conclude that it has moved inside the event horizon. This is the “no-drama” postulate of black hole complementarity.
The infalling actual half of the produced pair is likewise expected to continue to evolve under the ordinary laws of quantum mechanics, although those are not known at and very near the centre of a black hole. As the local mass-energy shrinks and the horizon recedes in consequence, the configuration of the system (notably its internal pressure and the density of quantum states) inside the event horizon becomes relevant.
The “information of the particle swallowed” comes from the state of the various fields, including the gravitational field, when the pair itself was created. If the no-hair theorem is valid (classically, semi-classically and in quantum gravity), the half-pair radiation in the vast majority of models by which the pairs can arise depends only on the mass, angular momentum and charge of the black hole. “Ordinary” objects’ blackbody radiation depends on other factors; indeed, that’s what makes the CMB so interesting. That, roughly, is the basis of the information paradox: Hawking radiation does not reveal what’s “inside” the blackbody radiating it, whereas ordinary blackbody radiation does.
Finally, that “black holes are not exactly black” does not remove the practical difficulty that astrophysical black holes are very very dim, and currently we can only spot astrophysical black hole candidates by looking for the energy signatures of things falling into them, and maaaaybe via microlensing. Sadly, therefore, only a handful of candidates at various masses have yet been found, so no-hair remains a conjecture.
That is the key doubt (or doubts, actually) I have regarding my question:
What conditions are required for pairs of particles to be entangled?
Do these pairs of particles (that give rise to Hawking radiation) comply with these conditions for entanglement? what % of the pairs of particles (that give rise to Hawking radiation) could comply with the conditions for entanglement?
It’s easy for particles to be entangled; all they have to do is interact or be created together. Yes, the particle that is produced in Hawking radiation is always entangled with the one that goes in; so in that sense the answer is 100%. But to be absolutely precise about this and track all the entanglement and all the information — no one can do that, which is the source of the problem.
Thanks for all the effort you put into posts like this. I’m not a physicist and very much appreciate the help your site has given me in getting through (and sometimes beyond) popular books on physics for the “lay” person. One thing you mention is the possible involvement of gravitons in Hawking radiation. I remember in earlier posts you referred to gravitons as particles whose existence is merely conjectural (in “The Known (Apparently-) Elementary Particles” you exclude them from your diagrams). However, several books I’ve read assert, without qualification, gravitons exist; others are doubtful, or simply exclude them from the Standard Model. In an earlier reply to this post you said “You’re confusing the virtual gravitons (which aren’t particles) that make up the gravitational fields with real gravitons that can carry energy out of the black hole.” Have you been won over to the reality of gravitons? If you have time, could you briefly give us an update on what the current arguments are for their existence? Thanks again.
It’s hard to say this in a way that sounds unambigous.
Theoretical calculation: General relativity predicts gravitational waves.
Experimental observation: we seem to see the effects of gravitational waves in the orbits of certain neutron star pairs, so gravitational waves are probably real.
Theoretical calculation: In any quantum theory, all waves are made from quanta. Therefore, if the world is described even roughly by a quantum theory [which it seems to be], then gravitational waves will be made from quanta: gravitons.
Experimental observation: missing; gravitons have not been observed, nor will they be observed soon, due to the extreme difficulty of measuring such weakly-interacting particles.
So you see: we have a very strong theoretical and experimental argument that gravitational *waves* exist; we have a strong theoretical argument that such waves will be made from *gravitons*; but we lack experimental confirmation, so it’s important to remember that the logic is, in the end, based on theory, not on experimental data. In that sense, gravitons are simply conjectured. But it’s really hard to believe they don’t exist, given the strength of the theoretical argument.
Finally, the Standard Model, by definition, includes all the forces except gravity, so by definition it doesn’t include gravitons. That’s got nothing to do with whether we think gravitons exist or not.
As to my comment today: the questioner assumed gravitons exist so I ran with him on it. It was not important, in that context, to emphasize that one is making a (very plausible but not verified) assumption.
Thanks very much. All your comments were useful, but especially: ” . . . the Standard Model, by definition, includes all the forces except gravity, so by definition it doesn’t include gravitons. That’s got nothing to do with whether we think gravitons exist or not.” Important distinction I hadn’t really thought about!
In Polchinki’s Sept. 2012 article on Sean Carroll’s blog, he considers the possibility that “Hawking evaporation is actually due to production of entangled pairs, with one of each pair escaping and one staying behind the horizon,You allude to entanglement briefly.
Due to entanglement, the information contained in ‘inside’ halves of entangled pairs, can in theory be retrieved from the outside halves. If the outside halves contribute to the hologram which is not leaked, I believe, the “halfway problem” seems to be avoided. My main problem with this interpretation, if I have understood it correctly, is that not all matter inside a back hole can be supposed to be made up of halves of entangled particles.
I have question regarding the information paradox: could the information on the whereabouts of the particles swallowed by the black hole be sent outside of the black hole by its paired particle through quantum entanglement?
Is that consistent or theoretically possible?
Are we absolutely sure that the problem is not about the Hawking radiation? No radiation – no paradox (without rewriting state-of-the-art-theories). Since something MUST be wrong…
I’m no physicist, as you can imagine! 😉
It’s a good question; but indeed, we have a LOT of evidence that black holes radiate. First, although Hawking’s calculation was a tour-de-force of its day, it’s now a standard calculation for any quantum gravity theorist, and so it’s been checked again and again. Second, and more importantly, the principles that lead to the existence of Hawking radiation are very simple and profound, at least from the point of view of a physicist. The issues are related to the fascinating fact that there are extremely strong analogies between the entropy and temperature of hot systems [like a gas of molecules in a box] and black holes — some of the equations are actually the same. And just as hot systems radiate energy, one would expect black holes to do so. Indeed this intuition guided Hawking to do the calculation. And the field/string correspondence I mentioned gives many concrete examples of this analogy.
The paradox only arises when one assumes that black holes not only radiate but also evaporate completely. But we have a significant amount of evidence for that too, now, thanks to the field/string correspondence… there’s no sign that small black holes stop radiating.
So I’m quite sure that large black holes that aren’t changing rapidly do radiate. I’m not sure what happens when they’ve undergone a significant amount of evaporation, however.
Matt, there is no evidence that black holes radiate. And there is no evidence that they evaporate completely. Mathematical hypotheses are not evidence. And like Piermatteo said, no Hawking radiation, no paradox. How can there be any Hawking radiation when gravitational time dilation goes infinite at the event horizon? Where the coordinate speed of light is zero, which is why the light doesn’t get out? When even Sabine knows that the “given” explanation for Hawking radiation is junk, and you can’t explain it to your grandmother? How can it be a tour-de-force when it ignored general relativity from the off? How can the elephant go to the end of time and back and be in two places at once? It can’t. There are no paradoxes. But there are mistakes. And when you have eliminated the impossible, whatever remains, however improbable, must be the truth.
Clearly there are some “short cuts” and “wrong turns” in the theories of quantum black holes, not only with the “evaporation” theory, since a bunch of the best subject matter experts in the field can’t find a solution to this issue, and can’t even agree on a common set of features and behaviours, and that is the reason why there are different proposals to this issue.
Regarding the fact that we do not have direct experimental confirmation of Hawking radiation, which is true, that does not invalidate the theory.
When Glashow, Salam and Weinberg were awarded the Nobel Prize for their electro-weak theory, at the time there was a small amount of indirect experimental validation of the theory. The theory predicted three different types of vector bosons (W+, W- and Z), and it also predicted a phenomenon called neutral currents.
The only experimental validation at the time was that neutral currents have been detected, but it took a while to validate the claim.
In fact, at the time, there was no proper collider in existence with the right design to detect the “Wees” and the “Zees”.
It took some more years to have the proper colliders, to run a healthy amount of collisions to scan “the terrain” and find these guys.
Even when the Wees and the Zees were found, there was an experimental gap, since the electro-weak theory was solidly based on the BEH mechanism, and the Higgs boson was still missing: at high energies, the Wees, the Zees and the photons are all the same type of particles and there is only one type of force (let’s call it the “electro-weak” force), and it is the Higgs field that makes the Wees and the Zees massive and the photons massless (the Higgs field “selects” them out), and from that point on, the weak nuclear force and the electro-magnetic force are different.
The theory of inflation does not have direct experimental validation, but it has predicted many phenomena that later have been experimentally validated, which clearly are indirect validations of it. Could we ever directly validate inflation? maybe, maybe not.
Gaston: there is no evidence for Hawking radiation. Comparing it to electroweak or vector bosons or inflation doesn’t change that. You could use the same argument to support the case for fairies and unicorns. It does not convince.
There was also no evidence for Higgs bosons, for 50 years. And yet: what do you know!? Turns out that theoretical physics works sometimes…
Exactly! Spoken like an expert.
Thanks for this and your other articles, which are invariably very interesting. When you say that information is not lost in quantum mechanics, does this include the projection (“collapse of the wave function”) which is applied when measurements are taken? I have only a vague understanding of what information means, but it seems to be that the projection does destroy information, and your remark of a quantum theory only making sense when the probabilities sum up to one may be taken to refer to the unitary evolution of the state.
It does not include the measurement process. The conservation of information applies merely to the evolution of the wave function that describes the process, and does not refer to how the information would actually be gathered. The fact that this conservation of information is therefore a formal, mathematical property, and not one that really could be tested experimentally in a direct way, certainly raises some issues as to whether it’s really something we should hold on to. But of course it’s one thing to raise questions, quite another to provide answers.
I hope BH are not chaotic i.e extremely sensitive to initial conditions! Then every BH may be different!
Every black hole probably is different, when looked at in detail.
If quantum mechanical effects in black holes are significant enough for black holes to strongly behave according to the rules of QFTs, we could argue that the multiple stories of QFTs work in favor of the idea that all black holes are really different and unique.
If this is proven to be true, it does not seat well with the No-Hair Conjecture for black holes.
I don’t think many people still believe that the No-Hair Conjectures, which are true for classical black holes, are true of quantum black holes.
Really? I think there would be broad agreement that there is no limit to the number of parameters (“stable hair”) that can be had by a stable black hole in AdS space, but that is not quite the same thing. The unlimited number of parameters raises some questions as to how they are fixed, whether they’re gauge invariant, and whether they are even measurable at long distances (“infinity”, for example).
In asymptotically flat space, there are few stable hairy black holes, and those are describable by a small number of parameters. Although you are right on the strictest reading of “no-hair conjecture”, the spirit of the conjecture lives on.
Perhaps the conjecture has just evolved into something like this pretty statement:
“The ‘no hair theorem’ … encodes our failure to find any alternative to the black hole geometry”
[Mathur’s slide 30 @ http://www.phys.virginia.edu/Announcements/Seminars/Slides/S2170.pdf ]
The emissions spectrum of an isolated massive neutron star would be an interesting thing to compare with that of an isolated stellar black hole. We seem to have the former in The Magnificent Seven (of which the prototype
http://en.wikipedia.org/wiki/RX_J1856.5-3754-3754 has so far delivered us a featureless pure BBR), but so far not the latter. The featurelessness is key: is information about the components of the collapsed star actually hidden to some set of outside observers? Is “no hair” sudden, or is it a sort of progressive balding?
So does the firewall prevent the black hole evaporating any further?
Well, first, let’s remember it’s not clear there is a firewall at all. And second, no, it presumably does not, and shrinks along with the black hole. But no one can calculate the details. Hawking’s 1974-1975 calculation does not directly depend on the presence or absence of a firewall.
Can you be more precise than ‘burned to a crisp’? What happens to an object after it hits the firewall (if it exists)? Does it get smeared along the firewall and not go beyond the event horizion?
Does this also say something about ‘conservation of information’ if loss of half the mass means loss of more than half the information? Or is that the whole problem?
No, I can’t be much more precise. First, there may well be no firewall at all, and even if there is one, there’s no clear set of theoretical equations that define a firewall… or equations that tell you what happens to something that hits one. All we really know is that, with simple but not necessarily correct assumptions, an infalling object gets blasted with arbitrarily large amounts of energy as it gets too close…
I don’t have a smart answer for your last questions; this is partly because I’m not quite enough of an expert to say something sensible off the top of my head, and partly because I think your questions would have to be rephrased to make them meaningful. If I can think of something to say I’ll come back to this.
[By the way, the halfway point is when the *area* (not the mass) of the black hole has shrunk by half.]
Thanks for the answer. Let me try again with my second question:
A photon with information content i1 falls into a black hole. Later on, another photon with information content i2 exits as Hawkins Radiation. Are you saying that i1 < i2? Or does i1 = i2, but we reach a point where the new smaller event horizon is too small to encode the remaining information?
I’m also thinking about information as a computer scientist would, maybe that is different than a physicist thinks about it.
Hmm… The problem cannot be phrased as i1 < i2. The problem is that i1 itself has to emerge. Information is not something you add up; you can’t afford to lose some information and replace it with some other information to make up the difference.
Moreover, no one photon carries off i1. At best, i1 will be stored in the correlations among various photons that emerge at different times.
Frankly, I’m not entirely clear on how to relate “information content” in the context of black holes to Shannon-type information theory. Some of my colleagues probably understand that better than I do.
Not entirely, because these gravitons should be responsible for all the enormous gravity coming out of the centre of the black hole nucleus . My suggestions is that the zero point vacuum energy ( casimir) should play an important role also for the black hole gravity.
You’re confusing the virtual gravitons (which aren’t particles) that make up the gravitational fields with real gravitons that can carry energy out of the black hole.
Thanks Matt great article. But what does the graviton of the standard model? Can it leave the black hole nucleus? as radiation resposnible for all of this?
Gravitons, along with photons, neutrinos, and other low-mass or massless particles are emitted as part of the Hawking radiation. I’m not sure if that answers your questions.
Matt: I asked this question before. So excuse me for raising it again.Changing sign of CC (Lambda) in ADS may be a big change. I am surprised that none of the experts think that trusting conclusions based on ADS (negative Lambda) for which there is no experimental evidence, unlike positive Lambda for which there is experimental evidence, would be a serious matter.
It’s a serious matter, but the matter has been considered, and the consensus is that it’s not, for this particular question, essential. Could the consensus be wrong? I suppose it is possible.
Good article Matt. I’d say it describes the situation well. But I have to say I think the problems stem from a misinterpretation of black holes. Remember I said a vertical light beam doesn’t curve round and it doesn’t slow down? So why doesn’t it get out? You referred to the waterfall analogy. But the vertical light beam isn’t like some fish in a waterfall. In no way is space falling inwards in a gravitational field. We don’t live under a chicken-little sky that’s falling in. No. IMHO the light doesn’t get out because at the event horizon the coordinate speed of light is zero. Because the original ‘frozen star’ black hole interpretation is the right one. See Kevin Brown’s Formation and Growth of Black Holes where he refers to it. He doesn’t favour it, but he does say it’s one of two interpretations provided by GR. I think it’s the one Einstein would have backed, because Einstein repeatedly referred to the speed of light varying with gravitational potential, and not just in 1911.
Hi John,
So why doesn’t it get out?
Here’s one way of looking at it that doesn’t involve thinking in terms of a changing speed of light. I’ll assume you accept that gravitational redshift occurs, i.e., that the wavelength of a light beam emitted from the surface of a massive object increases as the light “climbs” out of the gravitational “well,” and moreover that redshift is greater for more massive emitting objects than for less massive ones. So take this idea to an extreme. As you increase the mass of the emitting body, the wavelength as measured at some large distance from the source becomes greater and greater, at some point approaching infinity (i.e., the light has zero frequency). I think I remember you saying you are an electronics engineer, so you would agree that an electrical waveform of zero frequency is just a constant voltage. That is, the redshifted wave has become indistinguishable from no wave at all: the light has effectively not escaped from the gravitational field of the emitter. (Even if you want to argue that a light wave of zero frequency is still a light wave in some abstract sense, you would presumably agree that such a wave carries no energy and thus does not exist in a practical sense.)
Perhaps it seems the wavelength should approach infinity in an asymptotic sense, i.e., as the emitter mass grows without bound. That would be true if there were a linear relationship between the increase in mass and the wavelength, but general relativity is not a linear theory like Newtonian gravitation is — in GR the gravitational field itself acts a source of gravity…
Thanks Prof. Strassler! This is proof that “what is well conceived can be spelled out clearly” (translated from a French verse by Boileau…), even without equations.. But I still believe that a solar mass black hole will also be a spectacularly-dark one! Anyway, it’s good John Wheeler passed away still believing in the adequacy of the term he coined in all cases…
Great article!
A very good approach to explain this problem to laypersons.
Regarding the complexity mentioned by Hawking that appears inside the black hole, is it the result of the multiple stories of quantum field theories piling up? or is it just classical entropy doing its job?
The complexity is just classical chaos, if I understand him correctly. But I have not followed his work on the role of chaos in general relativity.
It is my understanding that the main formula pertaining to this (from the perspective of the outside of a black hole) is the so called Bekenstein-Hawking equation, that expresses that the entropy of a black hole is proportional to the surface of the event horizon.
For classical entropy and black hole entropy, the equations have the Boltzmann constant multiplied by an adimensional factor.
In the black hole formula, the adimensional factor is the area of the event horizon divided by the square of the Planck length (there’s also a constant with the value of 4 dividing).
If we make a conceptual comparison of both formulas for entropy (the classical equation and the black hole equation), it makes sense to assume that the number of different microscopic states that correspond to the same macroscopic state, which are related to the complexity of the system that gives rise to entropy is related to the area of the event horizon (there is a logarithmic scale difference between the two factors, but let’s skip the details for the moment): a larger event horizon means a larger complexity within the black hole.
If the universe is an ensemble of ordered system then what is the function of black holes (in the grand scheme)?
I know recent data indicate the universe is flat, (open), but assume the universe is a large expanding shell. The ratio of a volumes of a sector of the shell subtended by 2 x Radius (nominal) to the total volume of the shell is 1/pi, which is equal to 0.3183. Now assume a uniform density and hence the sector is 31.83% of the total mass of the shell.
Estimated distribution of matter and energy in the universe, today is 4.9% atoms and 26.8% dark matter, so the total mass of visible and dark matter is 4.9 + 26.8 = 31.7% ! Amazingly, the two numbers are very close, coincidence or linked? Assume, now the radius of the shell is 13.7 billion years and one could make the assumption the universe is an expanding shell.
So, what is the function of “black holes” in such a universe?
@Oaktree,
IMHO, your first sentence is not proper in more ways than one. Let’s see.
From the way I see, that sentence seems to imply that our universe has a purpose to serve, to achieve, which is not something that Physics would care or could care to study.
Our universe, at all levels, presents behaviour and science in general cares to study that behaviour and how to better describe it so as to be able to predict how it may behave under certain circunstances, like for instance, in the future.
Besides this, in this blog there are many articles that clearly describe how our universe is full of all sorts of broken symmetries which are intimately intertwined with break ups of conservation laws. Due to these break ups of conservation laws there is some degree of disorder in many aspects of our universe, so, at some level, we can’t substain an argument about “an ordered system”.
Let’s have an example with the signal from the microwave background radiation.
For one thing, there value of temperature everywhere in the signal, even though it has tiny variations, is incredibly uniform, even when comparing parts of the universe so far apart from each other that it is not possible that in such a short length of time since the Big Bang all those distant spots could equalize there temperature.
But at the same time, this signal is full of variations everywhere, variations that are called anisotropies.
These anisotropies, scientists believe, are the seeds of the clusters of galaxies that today exist.
So, we exist because of this level of disorder that gave rise to the anisotropies.
This gives me the cue to deal with how there are black holes, which seems to be part of your initial question.
At a certain level, the fact that stars end their lifecycle in a gamut of final states, depending on their mass, like say red dwarfs, neutron stars, or black holes, is somehow a consequence of the difference in strength and range of the diverse forces of nature.
The combination of how massive a star is, with how the different forces of nature interact when a star runs out of nuclear fuel and collapses, gives rise to this gamut of final states.
Let’s consider briefly an analogy: a liquid like water flowing through a pipe. The main forces acting on the liquid are inertial forces and viscous forces. How these two forces compare in relative strength will determine the main behaviour of the flow, from being “nice” or laminar (inertial forces are much larger than viscous forces), to “intermediate” or transitional (inertial forces are still larger than but comparable to viscous forces), all the up to being “unsettling” or turbulent (viscous forces are much larger than inertial forces).
Here we also have a gamut of states for the flow, which is the result of a combination of the forces at play, and there is nothing wrong with the universe because of the existance of turbulent flow, it just how the universe behaves (or at least, a very tiny fraction of the universe).
Regarding your geometrical deduction, there is a few details that, from the way I see it, do not add up.
To start with, at this stage in the life of our universe, it is “flat”, but it was not so during the first half of its current lifetime, so, whatever your numerical coincidence wants to imply does not apply for more than half of the lifetime of our universe.
Besides, our universe is “flat” in four dimensions, with one of those four dimensions being time, so, your numerical deduction is missing more than a few elements to be a workable proof of value.
First, everything we see and measure (information) has a cause (causality) and hence must have a purpose in the total system (grand scheme). We live in a 3D universe and time (Schrodinger’s time) is merely a quantization of causality. We exist only in “now” in a “sea” of complex changes of energy states.
Second, “order” for me is change, dE ≠ 0, hence something different will happen and create a system since it will follow a “law” (purpose). Chaos, dE = 0, no change hence, since energy is conserved, a “singularity” with a very high temperature in a very small space.
Space must always be spherical because of the symmetrical nature of the universe and the governing conservation laws. i.e. in a spherical shell universe any point (mass) inside the shell has a resultant F = 0 and the force of any point (mass) outside the shell is F = – (GmM)/r2 , hence both the inner and outer surface boundaries of a spherical shell universe is govern by the gravitational field, only!
But, the universe, the shell is expanding, why? One view is that changes are obviously still occurring, 4.9% atoms, but maybe these atoms are depleting and converted back “down” into dark matter and inturn down to dark energy hence stretching the galaxies apart which will cause the shell to expand because the local pull of matter on the surfaces is reduced.
So, if atoms are converted “down” to dark matter then black holes would be a good place to start looking for ports (orifices). I say this because “dark” could very well be the “loss” of information (stable particles govern by the speed of light). So what would be the prime candidate of breaking up these particles, gravitational field. But this field has the lowest strength of all the fields we know of? Yes, and is precisely why it must be this field because it has the highest resolution to break up the atoms ( cancel the g-factors). And black holes are regions where the gravitational field reaches maximum and/or a threshold capable of breaking up the strong force. Hence black holes could be viewed as a chaotic orifice from light to dark.
Indeed, the generalizations as described by Prof Strassler help a great deal to us laypeople.
Reading all these arguments (the fine details) that are trying to put the puzzle together, the discussion, or the Grand Scheme, is that there is no unanimous convergence to understanding the grand scheme of nature.
My question is could the discussion on black holes be done outside the context of dark matter and dark energy? I refer you to the mass distribution of the galaxy cluster, CL0024. When I see the plot, inverted 3D mass/area, I immediately think of a possible analogy, correct me if I am wrong, of ocean waves. Peaks (valleys), galaxies, are the whitecaps “breaking” atop of huge waves, dark matter, transversing in a very, very big ocean, dark energy. Like the whitecaps “falling” back into the wave by the force of gravity could the galaxy be falling back into dark matter? Is visible matter dissipating down to the ground state (ZPE) through this very chaotic, (the scrabbling of information is due to the gravitational field reaching its upper limit), orifice we call a black hole?
Could this also explain the “expansion” of the visible universe? The hot energy slowly dissipating down and the growing dark matter “stretching” space-time and hence we (living on the surface, whitecaps) see the galaxies drift apart.
“Black holes” are not just in center of galaxies, but any region where the gravitational field reaches its limits, like supernovae.
Are we living on whitecaps?
I repeate “the generalizations as described by Prof Strassler help a great deal to us laypeople”.
Mr.Oaktree, Iam also have nearly the same conception.
There is conservation of information in what we call space time. Otherwise the radiative photons will slow down. The statistical properties of the Hawking radiation, as usual in quantum theory, is the problem – also cannot be solved by non functioning of relativity in black hole situation.
Like dark matter, the black hole radiation is “non-thermal (not even black-body radiation)”. Information deposited prior to the half-way point remains concealed until the half-way point (massively entangled), and then emerges quickly. So firewall (thermal radiation) is imminent.
But if the information is scrambled (violate information causality), which really becomes space inside the black hole (may contain information of Retrocausality or decrease in entropy), make the firewall (thermal radiation) into new space – means, “sudden expansion of space” ?
Indeed, I wonder what Prof. Strassler’s thoughts are about this?
Adding one more point, you would expect the fundamental force of nature, I assume to be the gravitational field, since it is the weakest (highest resolution), at its maximum intensity, flux, to be the only one capable of scrambling the energy states down to the fundamental parameters, “space-time”.
Here is another question: Are WIMPs, gravitons? … Which leads to another much more fundamental question which I will ask in a discussion about gravitons.
Wow guys you’ve figured it all out. I look for to your scientific papers on the subject and all all the accompanying mathematical and experimental proofs that they most assuredly will contain.