© Matt Strassler [April 28, 2014]
Let me start by asking you a couple of questions with simple, intuitive answers.
Let’s take a bowl and a marble (Figure 1). If
- I want the marble to remain stationary after I place it in the bowl, and
- I want to make sure it will remain in the same vicinity if I move the bowl slightly,
where should I put it?
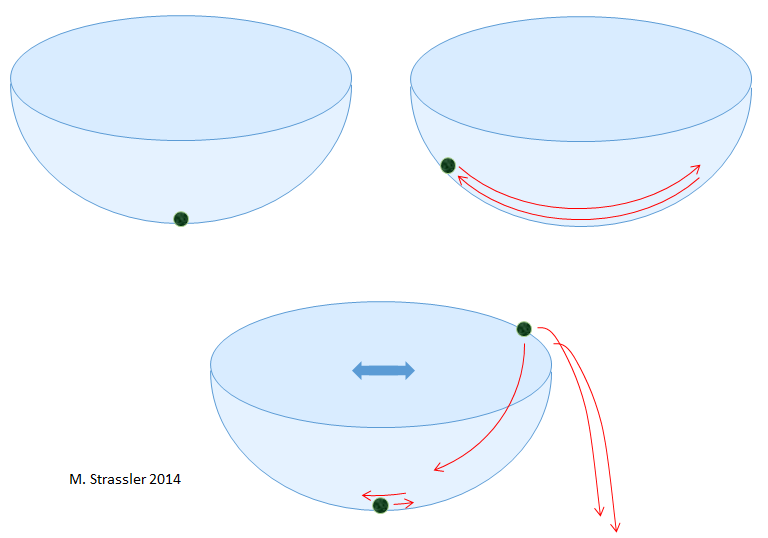
Of course, I need to put it in the center, right at the bottom. Why? Intuitively, if I put it anywhere else, it will roll down toward the bottom, and swing back and forth. Eventually, friction will reduce the height at which it swings, and will bring it to a stop — at the bottom.
In principle, I could try to balance the marble on the edge of the bowl. But if I jiggle the bowl at all, the marble will lose its balance and fall off. So that’s not a place that satisfies the second criterion in my question.
Let’s call a position at which the marble can remain stationary, and from which it will not dramatically depart if the bowl or the marble are moved slightly, a “stable location for the marble.” The bottom of the bowl is such a stable location.
Ok, here’s another question. If I have two bowls, as shown in Figure 2, where are the stable locations for the marble? That’s easy too: there are two places, namely, the bottom of each bowl.
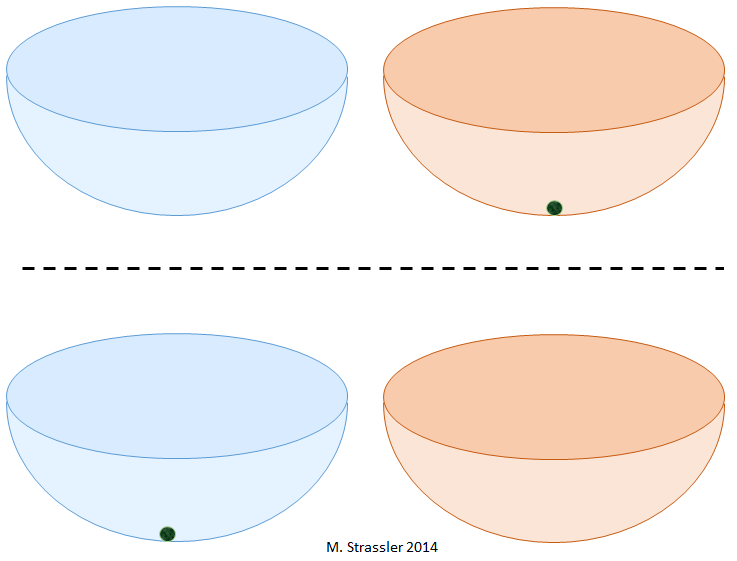
Finally, another one with an intuitive answer: If I place the marble in the bottom of bowl 1, and I then leave the room, seal it shut, ensure that no one goes in or out, and check that there have been no earthquakes or other disturbances, then what are the chances that, ten years later, when I open up the room again, that I would find the marble in the bottom of bowl 2? Of course, it’s zero. For the marble to move from the bottom of bowl 1 to the bottom of bowl 2, someone or something would have to pick up the marble and move it from one place to the other, carrying it over the lip of bowl 1, across to bowl 2, and over the lip of bowl 2. So it’s obvious the marble will still be in the bottom of bowl 1.
Obvious and essentially correct. Yet in the quantum world we live in, no object is ever quite stationary for more than an instant, nor is its location exactly knowable. So one of these answers isn’t quite true.
Tunneling
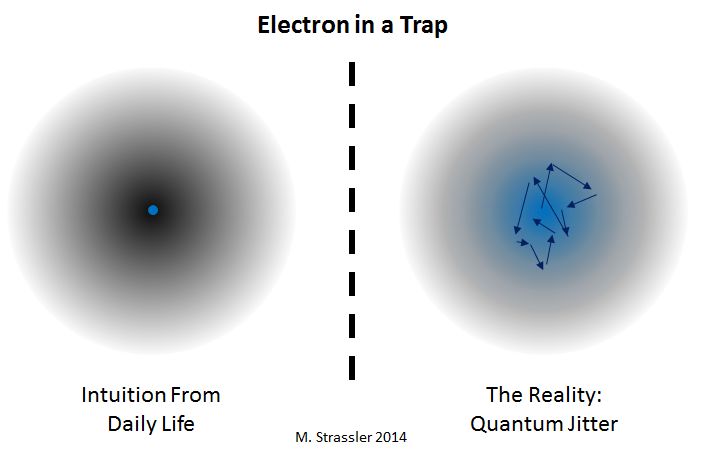
If (Figure 3) I put an elementary particle like an electron in a magnetic trap that acts like a bowl, tending to push the electron toward the center just the way gravity and the walls of the bowl push the marble toward the bowl’s center in Figure 1, then what is a stable location for the electron? Just as you would intuitively expect, the electron’s average position will be stationary only if I place the electron the center of the trap.
But quantum mechanics adds a wrinkle. The electron cannot remain stationary; there is a sense in which its location is subject to a sort of “quantum jitter”. This causes its position and its motion to be constantly changing, or (better) even to be undefined, by small amounts. [This is the famous “uncertainty principle” in action.] Only the average position of the electron is at the center of the trap; if you look for the electron, you’ll typically find it somewhere else in the trap, near but not at the center. And the electron is only stationary in the following sense: it’s typically moving, but its motion is in a random direction, and since it’s trapped by the walls of the trap, on average it goes nowhere.
That’s a bit weird, but it just reflects the fact that electrons aren’t what you think they are, and don’t behave like any object you’ve ever seen.
By the way, it also assures that the electron cannot be balanced on the edge of the trap, in contrast to a marble on the edge of a bowl (as in Figure 1, bottom). The electron’s position isn’t sharply defined, so it can’t be precisely balanced; and so, even without the trap being jiggled, the electron would become unbalanced and almost immediately would fall off.
But the weirder thing is what happens if I have two traps, separated from one another, and I put the electron in one trap. Yes, the center of either trap is a good stable location for the electron. That’s still true… in the sense that the electron can stay there and won’t run away if you jiggle the trap.
However, if I put the electron in trap number 1, and walk away, sealing the room etc., there’s a certain probability (Figure 4) that when I come back the electron will be in trap number 2.
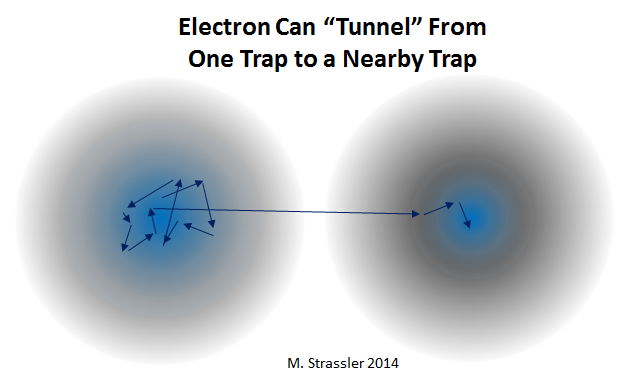
How did it do that? If you imagine that electrons are like marbles, you will not be able to understand this. But electrons are not like marbles [or at least not like your intuitive notion of a marble], and their quantum jitter offers them an extremely small but non-zero probability of “walking through walls” — of going someplace that it would seem impossible for them to go — and ending up on the other side. This is called, poetically, “tunneling” — but you should not imagine that the electron digs a hole through the wall. And you’ll never catch the electron in the wall — in the act, so to speak. It’s just that the wall isn’t completely impermeable to things like electrons; electrons are not things that can be easily trapped.
Actually, it’s even crazier than this: because what is true for the electron actually is true for the marble in the bowl. The marble could end up in bowl 2, if you could give it enough time. But the probability of this happening is extremely extremely extremely small… so small that if you waited billions of years, or even billions of billions of billions of years, that still wouldn’t be enough. For all practical purposes, it will “never” happen.
The point is that our world is a quantum world, and all objects are made from elementary particles and are subject to the rules of quantum physics. Quantum jitter is ever-present. But for most objects that have a lot of mass compared to an elementary particle — a marble, for instance, or even a typical speck of dust — this quantum jitter is too small to observe, except in very specially designed experiments. And the consequent ability to tunnel through walls is also, therefore, never seen in ordinary daily life.
To say it another way: any object can tunnel through a “wall”, but the probability for it to do so typically goes down very rapidly if
- the object has a large mass
- the wall is thick (i.e. there is a long distance between its two sides)
- the wall is hard to penetrate (i.e. to punch through the wall in the usual way would require a lot of energy.)
For a marble to penetrate the lip of a bowl is possible in principle, but in practice might as well be impossible. For an electron to escape from one trap to another may be easy, if the traps are close together and the traps are not very deep, but it may be very difficult, if the traps are far apart or the traps are very deep.
Are We Sure Tunneling Really Happens?
Is this tunneling effect just speculation? Absolutely not. It’s fundamental in chemistry, takes place in many materials, plays a role in biology, and it is the principle used in our most clever and powerful microscopes.
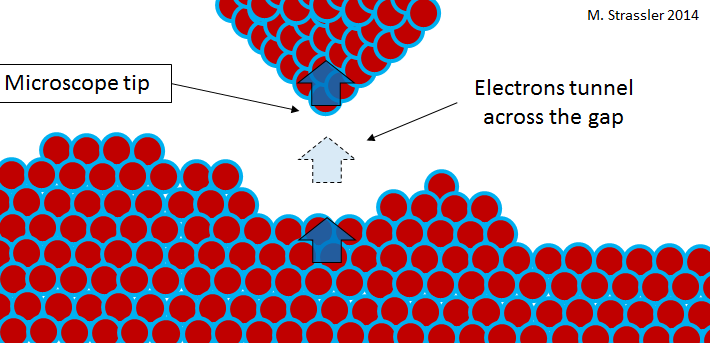
For brevity, let me just focus on the microscope. In Figure 5 is a picture of atoms made using a scanning tunneling microscope, or STM. Such a microscope has a narrow needle whose tip moves just above the material that is being studied. (See Figure 6.) Both the material and the needle are, of course, made from atoms; and on the outskirts of the atoms are electrons. Roughly speaking, the electrons are trapped within the material under study, or trapped within the tip of the microscope. But the closer the tip is to the surface, the more likely the electrons are to tunnel from one to the other. A simple arrangement [for those who want to know: a voltage difference is maintained between the material and the tip — and see further discussion in the next section] can assure that the electrons preferentially flow from the surface to the tip, and this flow is an electric current, one that can be measured. As the tip moves over the surface, and the surface is closer to or farther from the tip, the current changes, becoming stronger when the distance is smaller and weaker when the distance grows. By monitoring the current (or, alternatively, by moving the tip up and down to keep the current constant) as the tip sweeps across the surface, the microscope infers the shape of the surface, often with enough detail to see its individual atoms.
Tunneling plays many other roles in nature and in modern technology, which perhaps I’ll return to later. Soon I’ll discuss some of its implications in particle physics.
Tunneling Between Traps of Different Depths
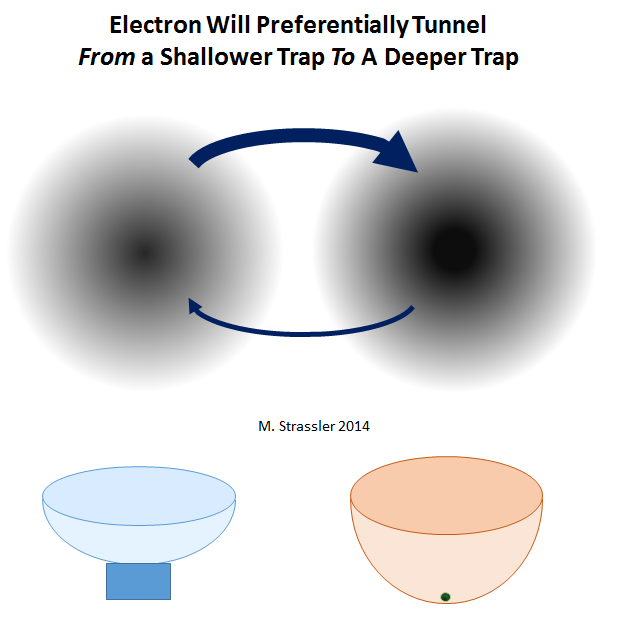
In Figure 4, I implicitly assumed that the two traps were of equal depth — just as the bowls of Figure 2 were of the same shape. That means that an electron in either trap is equally likely to tunnel to the other one.
But let’s now suppose that one of the two traps for the electron in Figure 4 is deeper than the other — similar to imagining that one bowl in Figure 2 is deeper than the other. (See Figure 7.) Well, although the electron can tunnel in either direction, it is much easier for the electron to tunnel from the shallower trap to the deeper one than the other way round. Consequently, if we wait long enough, so that the electron has plenty of time to tunnel in either direction and back again, and then we start doing measurements to find out where the electron is, we will find the electron most often in the deeper trap. [There are some subtleties to this statement; the full story depends also on the shape of the trap, not just its depth, but this is good enough for now.] In fact, the difference in depths doesn’t have to be that large before the tunneling from the deeper to the shallower trap becomes extremely rare.
In short, tunneling will generally occur in both directions, but it is much more likely to occur from a shallow trap to a deep one (Figure 7.)
In fact, this feature is just what is used in the Scanning Tunneling Microscope to make sure the electrons tend to flow only in one direction, as indicated in Figure 6. Essentially, what is done is to make the tip of the microscope a deeper trap than the surface under study, so that the electrons prefer to tunnel out of the surface into the tip, rather than the other way round. [The microscope also works if the reverse is done, with electrons tunneling into the surface more often than out of it.] The traps are made deeper or shallower by using a battery, which creates a voltage difference between the tip and the surface, resulting in an additional energy difference between the electrons in the tip and the electrons in the surface. The fact that it is so easy to force the electrons to tunnel one direction more often than the other is part of what makes tunneling so practically useful in electronics.


133 Responses
Essentially explained the STM. Thank you for the information!
This “electron jump” model looks similar to the random discontinuous motion approach of Shan Gao and others to me. If this is going to be a serious theory and not just an ad hoc apporach it should also reproduce the double slit experiment, so include the phase of the Schroedinger wave function. That would be interesting to see how interference could come out of this “jump” model. I was trying to find where Shan Gao has calculated this in his random jump model but could not find it so far. @Paul: I believe it’s more the “quantum jitter” of the particle that causes the tunnel effect while the atoms that make up the bowls correspond to large objects by comparison and their fluctuations can be neglected.
Using the analogy of the bowls, could quantum tunneling be due to the quantum fluctuations of vacua ie ‘the bowls’?
So that the ‘bowl’ jitters and change ‘shape’ and location? In other words the minima is moving and changing location?
Hi – I need to explain this to a bunch of 17-18 year olds. I think the analogy with the bowls is great and I will use it. However, the question I am often asked is this: we regularly get sparking with high enough potential differences – we only need to look at the Van de Graaf generator for this. Why then don’t electrons jump the gap in the STM in the same way that we get discharge in an air gap from a Van de Graaf generator? In other words, what prevents an electron from classically jumping the air gap in an STM when we know that with a high enough voltage, we can generate an electric field that will ionize the air and allow a current to flow anyway?
Just trying to grasp the concept. Which one is correct? Neither?
– The electron constantly moves. There’s a radius/region with very high probability that the electron moves into, but theoretically, he can move anywhere, so you have a chance to find him in Alaska 😛 . Thus, tunneling is nothing more than a stray particle
– Tunneling is a form of teleportation, so if you could (i know it’s impossible) follow a path of the electron, he disappears from x and instantly appears in y.
You have got interesting articles here. Your site can go viral, you need some
initial traffic only. How to get initial traffic???
Search google for: marihhu’s tips
Good afternoon, my name is Ayodeji IBITOYE a masters student of the University of Ibadan, Niogeria. In search for an head way in a research am doing presently i navigated my way into this place and quite appreciate the beauty of what you have done. Need help in my research. Currently working on my MSc thesis on relativistic quantum mechanics. From the solution of a single particle non-relativistic schrodinger equation for a finite potential well to a relativistic solution(Klein-Gordon), I thought of looking at how a particle trapped in a potential well can be liken to how photons gets trapped inside a shield used in protecting normal cells in radiotherapy….where the particle in a potential well is now the photons..Looking for the appropriate and suitable POTENTIAL to solve Klein-Gordon equation or how do i correctly go about this pls help.
Hello Professor.You are doing an awesome job. This was an awesome article.I am an MD but hugely interested in Physics. I want to self study it from scratch that is completely go through undergrad and grad physics courses. Can you please suggest books from where to start for undergraduate Physics? I am familiar with Mathematics and believe that I can grasp complicated mathematics though of course it will take time.
Thank you!
There are classical theories and quantum field theories.
An example of a classical theory is General Relativity (it presents the usual and expected aspects of classical theories, like localization and strict causality rules, for instance).
An example of a quantum field theory is Quantum Chromo Dynamics (it presents the usual and expected aspects of quantum field theories, like Path Integral solutions and a Born Rule, for instance).
The is a continuum of ideas, or a clear traceability path between classical theories, in particular, the classical theories that care to generalize Newton’s general rules of motion, and quantum field theories.
Kind regards, GEN
My personal view is (a) that one cannot make a physical observation to within a quantum of action. The issue then is,
(b) is the electron a particle in the classical sense that moves, only within a quantum of action we cannot describe such movement, or
(c) is it a dispersed field that localizes when we make an observation, e.g. an impact on a detector?
Unless you can falsify (a), I do not think you can directly tell the difference. All you can do is to construct theories based on whatever view you hold, make predictions, and see what is better. There are two problems then that I see, although maybe someone can show this not to be the case. The problem with (b) is that invariably you need something else to be there that you have difficulty detecting. The problem with (c) is that it is inherently plastic and is constrained only be a number of equations that do not necessarily arise automatically from the proposition. By that I mean, why do not other things happen? I think there is more work to do before this is all settled.
Gastón,
You wrote:
I would say that a good way to explain the expression “not moving in the usual sense” would be that in QFTs, particles do not move just like macroscopic bodies in classical mechanics.
But, while macroscopic bodies that are in motion behave in such a way that we can predict with a lot of precision the trajectory (both the future and the past) of them, based on their current data on dynamics and kinetics, we are not that lucky regarding (quantum) particles in quantum systems (both real systems and imaginary systems).
Kind regards, GEN
Isn’t there a huge difference in how we investigate things via the differences between quantum sized things and large macroscopic things? In macroscopic things we investigate their position and momentum by using things that are many many orders smaller in mass/energy such that what we impact the thing with hardly has any effect in changing its position or momentum. Things are quite different at the quantum level as the things that we use to investigate them with are similar in mass/energy levels and hence the very act of investigation changes the co-variables such that you can never good a good idea of both position and momentum at the same time. I don’t think this issue rules out that entities at the quantum level don’t move in the classical sense. I don’t care for any theory or interpretation that eliminates classical motion in favor of some kind of fuzzy thinking. Hell, there is enough fuzzy thinking in much of the public as things are now and it isn’t helpful.
Vince
Am I right to conclude that the phenomenon of static electricity is not quantum tunneling? I don’t know yet the mechanism that causes the migration of electrons between two electrically neutral materials, but the spark between my fingertip and the door knob tells me that the electrons are accelerating rather than tunneling and the radiated photons is the evidence of acceleration. Is my train of thoughts on the right track?
Electrons have differing affinities for all materials. As such when any two different materials are in contact electrons will move from one to the other until the electric potential balances this flow out. (This is what causes current to flow in batteries.) As a side effect of this you and all objects around you are charged. Not much, but some.
If a material is conducting the charge will disperse through the whole material or conduct away. If it is insulating ‘patches’ tend to build up where materials contact blocking further electron transfer. However if two nonconducting materials of significantly different electron affinity are quickly rubbed together then the transfer can take place over the entirety of both objects. This is aided by the energy of rubbing.
Discharging can in fact utilize tunneling, a slow and gradual process, but this is usually vastly outcompeted by more mundane processes. Direct contact, air itself ionizing and conducting or the charge ‘hopping’ across particles in the air. In these cases energy is emitted in various ways, the electrons themselves are moving, but small volumes of air can also become quite hot in temperature, electrons moving between energy levels in atoms can radiate and so on.
In answer to Dorothy’s question, and underlining the point made by Walter Davies, quantum tunneling is responsible for the existence of all of the chemical elements that were not produced in the early stages of the Big Bang. The most digestible and insight-fostering treatment I’ve encountered is A. C. Phillips, ‘The Physics of Stars’, Second edition, Wiley, 1999.
What about thermal motions of atoms comprising the trap? Is it not possible that their jitter transfers enough energy to the electron to let it traverse the barrier? In other words lets say we start with an electron in the first trap, after a while it tunnels to the second trap, will the total energy/temperature of the first trap decrease enough to account for the extra energy needed for the electron to traverse the barrier? I suspect it won’t cause there wouldn’t be anything strange about the whole process if it were the case but can anyone confirm it?
A trap needn’t be made out of atoms, magnetic fields will suffice. But the question is a valid one. There are two things we would expect to see if this were the case however. The first is the emission of particles from the trap. An electron given enough energy to ‘go over’ the barrier can do so in any direction it wants, it doesn’t need to only do so in the direction of the second trap. So if the trap *was* giving energy to the electrons we would expect to see them escaping the trap in all directions, not tunneling between two close traps.
The second thing we would expect to see is one trap cooling and the other warming; the energy from one trap would go to the electron, which would give that energy to the second trap, warming it.
We do in fact see both these processes if we ‘warm’ the trap enough (Like shaking the bowl with the marble in it.) but tunneling is not only not affected by this, but occurs when the traps are as ‘cold’ as possible.
Matt
Let us try thus thought experiment. Suppose an electron move from point A to B by the process of annihilation at point A and recreation at point B. If this process is randomly occuring it will generate a gaussian distribution pattern at the bottom of the potential well.The very act of annihilation and creation will switch on and off a gravitational field associated with the presence of the electron and therefore generate a gravity wave with a frequency equal to the electron Compton frequency. Question: Will the electron evaporate through graviton emission and therefore increase its Compton wavelength with time?
Stuart, this argument does not work. By an analogous argument you could conclude that for example the electron in the hydrogen ground state must emit electromagnetic radiation. This would be far easier to detect and we know it doesn’t happen. This is actually a point that puzzled people before quantum mechanics was established: Why doesn’t the electron radiate when it is moving around the nucleus and thereby undergoing acceleration? Part of the answer is that the electron in the ground state is not moving in the usual sense. The ground state is an unchanging state. Quantum jitter is not motion in the classical sense, and if you assume so, you come to wrong conclusions. It is just that a random jittery motion is the closest classical analogy that we have to visualize quantum fluctuations in a non-technical way.
I am not clear what you mean by the electron in the ground state (of hydrogen, say) is “not moving in the usual sense”. The state is clearly stationary, but if the electron were not moving in the usual sense, then there should be an electric moment; that there isn’t (unless you think the electron is not an object localized in much less space than the size of the atom) is surely evidence that it does move in the sense that it is not stationary in one place (which would violate the Uncertainty Principle anyway) and which in turn is motion in the usual sense, is it not ? The same surely applies to quantum jitter. Either electron is localized in that space required to define the size of a particle, which is less than the range of where it can be found, or it is not. Which is it?
It is the latter. An electron with well-defined energy in an atom is not localized on scales smaller than the radius of the atom (roughly). (Strictly it is not localized at all, but when you draw a surface along a constant probability density such that the electron is found inside with a probability of, for example, 99%, you get – for certain states – beautiful shapes like this: http://winter.group.shef.ac.uk/orbitron/AOs/6f/index.html , with a size on the scale that we call the size of an atom. Of course the ground state looks more dull, it is 1s.)
If you make the electron localized on a scale much smaller than the atom, the wave function in momentum space will be spread very wide due to the Uncertainty Principle, and the atom will fall apart with high probability. This is exactly what you observe when you direct radiation at the atom with a wavelength small enough to localize the electron on these small scales.
My statement about “not moving in the usual sense” should be taken with a grain of salt as it does not have a precisely defined meaning. As you say the ground state is stationary – that is a precise statement. On the other hand the expectation value for the square of the momentum (and so for the magnitude of the momentum) is not zero, which is also a precise statement. These are both true even though they cannot be reconciled in our usual (classical) intuition. So in some sense there is motion in such a state, but it is not like the electron being first “there” and then “somewhere else”.
I would say that a good way to explain the expression “not moving in the usual sense” would be that in QFTs, particles do not move just like macroscopic bodies in classical mechanics.
But, while macroscopic bodies that are in motion behave in such a way that we can predict with a lot of precision the trajectory (both the future and the past) of them, based on their current data on dynamics and kinetics, we are not that lucky regarding (quantum) particles in quantum systems (both real systems and imaginary systems).
Kind regards, GEN
That is what I thought you meant, but the curse of words is they can often be read to mean something differently.
I think there is too much talk of walls, traps, bowls, etc., which is doing more obscuring than elucidation. At bottom we are talking about protons and electrons. We know that an electron has an affinity to be relatively close to a proton and because of that we say each has a charge. No one has figured out why there is “charge.” We just know that this behavior occurs. We also know that everything is in motion. When we say that something is not in motion we only mean this in a sense that relative to our motion we don’t observe any motion that is different than ours. But, of course, when we examine everything microscopically there is jiggling going on. At the quantum level, this, I suspect, is due to bombardment of the photon field. Light can push comet tails and foil solar sails away from the sun. Light can warm your skin or burn it. Light has mass and falls in the presence of larger masses.
The uncertainty principle doesn’t lead to weird behavior in my opinion. Some physicists are confused by the principle to think that since we can not exactly determine two conjugate variables that there is a loosening of cause and effect. Here is what one person observed many decades ago:
“The implications of Heisenberg’s principle of uncertainty are often seriously confused owing to the expression ‘to determine’; [….] But every argument that, since some change cannot be ‘determined’ in the sense of ‘ascertained’, it is therefore not ‘determined’ in the absolutely different sense of ’caused’, is a fallacy of equivocation.”
–J.E. Turner, (Nature, No. 3191, Vol. 126, December 27, 1930, p. 995.)
The ripple or ripple is here, but the field is everywhere and the ripple should be able to move about the field as a ripple on the water providing that a force acts upon it? The act of measuring can reposition the ripple, or some other force acting on the electron, that is a ripple, or wave or fuzziness? At least that seems to make sense to me.
I meant the wave or ripple that is the electron is here.
If this doesn’t make sense it’s because the weekend has arrived and with it my brain has frozen. Anything for an excuse.
That is one way of looking at it. A particle always has some uncertainty in its position, it is not in two places at once but has varying probabilities of being in various places. When we measure it we ‘confine’ its location and after that it ‘spreads out’ again.
An electron in one trap has a small chance of being in the space of the second trap if that trap is close enough. When we observe the electron usually we will see it in the first trap, but sometimes we will see it in the second. When we see it in the second it ‘spreads out’ the exact same was as if it had always been there. As far as we can tell the electron has tunneled from one trap to the other though it hasn’t moved in the traditional sense.
Question; you state that large, classical objects can tunnel. I am curious as to the view of mainstream physics on this. As far as I am aware a big question is why quantum processes do not appear on classical scales. I have seen two possible solutions; first that they do but the probability is incredibly small, the possibility you seem to stand by. The second is that they do not, there is some sort of ‘cutoff’ due to something suppressing various processes in which case there is no chance at all, not even a tiny one, of a classical object tunneling. Which of these is the mainstream view? Is there any debate at all around this?
Kudzu: You can get large “classical” objects to behave like quantum sized particles. Take a large steel plate with many bowls on top and place a popcorn kernel (or anything else that can jump and not evaporate when heated) in each bowl. Place a heating element underneath the steel plate and then turn up the heat; for a while energy applied won’t be enough to cause the items to climb out of the bowls (let’s not be fixated on the mechanics of popcorn popping). When enough energy is applied the items in the bowls will climb or jump out of the bowl they were in and land in another one.
The uncertainty principle still applies.
In this case this is purely classical; the corn is given enough energy to move from one trap to another by moving against the barrier. And I know that while classical systems can approximate quantum behavior that is not my question; I question whether they do in fact have quantum behavior with a very low probability or whether they are purely classical for some reason.
Not as good as I’d have expected based on Matt’s otherwise unequalled presentations. For me, Atkins’s Physical Chemistry was the one that finally explained this. There was a graph of the wavefunction. The essential point was that for a finite barrier, the probability of being deflected *tends to* zero – but never actually *is* zero. Jitter as a simple motion is just a misleading classical analogy. I could win the state lottery 13 times a row – not zero but unlikely (cf. quantum barrier). But, I can’t win the lottery if I don’t play (a classical barrier).
So, is quantum jitter different than quantum fluctuations? In Matt’s page here: http://profmattstrassler.com/articles-and-posts/particle-physics-basics/quantum-fluctuations-and-their-energy/
He is saying there is a whole lot of energy in what we think of normal empty space. He writes: “But here’s the thing: those fields are never entirely quiet. Quantum fields never quite maintain a constant value; their value at any point in space is always jittering around a bit. This jitter is called “quantum fluctuations”, and just as for the particle in the tiny bowl, it is a consequence of the famous “uncertainty principle” of Heisenberg. ”
Although, surely those fluctuations happen even when we are not making measurements or philosophizing, otherwise, we might as well say that a tree falling in a forest with no one around to hear it doesn’t make a sound. The physics of the universe exists even if we are not here, but it than is meaningless.
They are both the same thing, what’s different is what’s ‘jittering’. In the case of ‘jitter’ a stable particle of specific (average) energy x is jittering. Its position and energy are uncertain. We can say ‘somewhere here is 1 particle of energy about x’
In the case of fluctuations it is the average zero value of a field jittering; ‘nothing’ is jittering. We can say ‘somewhere here is 0 particle of energy about 0’ Because ‘about 0’ is not ‘exactly 0 all the time’ there is some residual energy in every point of space.
Kudzu: For me that ‘nothing’ that is jittering is like air in a room with no audible sounds because we are not sensitive enough to hear that level of potential interaction. To my thinking all fields are composed of material entities. The uncertainty principle is just another layer of thought that gets added to the world out of necessity because the things that we probe the field with are massive when compared with what we are probing.
The probabilistic behaviour of electrons in atoms can be clearly verified with multiple measurements of electrons in atoms that are exactly in the same state.
You can create the multiplicity of measurements in more than one way, and as long as the state of the systems used to measure is the same, you will get the same probabilistic “image”.
Due to this probabilistic behaviour, you will not get the very same result of any given dimension when you do different measurements of the dimension (like say, position).
Hmmm, I’m talking about precision of the measurements, and not about the actual values of the measurements.
If you measure just one dimension, say position, you can have as much precision as your instruments allow you with no problem.
If you do another measurement, you may get a different value of position, but you can still have as much precision as your instruments allow.
Yes, you can theoretically measure a single observable, or even a set of compatible (commuting) observables with arbitrary accuracy. However, you cannot assume in general that repeating the same measurement (or set of compatible measurements) will consistently give you the same results. It depends on the rules governing the dynamical behavior of your system, namely on the Hamiltonian operator. If the observable you are measuring commutes with the Hamiltonian, you will get the same result consistently, theoretically without any jitter, as long as you do not otherwise disturb the state.
An example would be a free electron (no forces acting on it), where you can repeatedly measure the momentum and get the same result. (Not the position!)
In the case of the harmonic oscillator (or the “electron in the bowl”), the Hamiltonian commutes with neither the position nor the momentum operator. So while you can theoretically measure one of them with arbitrary accuracy at a single point in time, you will not get the same result when you repeat the measurement. Both position and momentum will jitter in this case, even if you do not measure both of them.
I like very much your explanation. Please let me ask: in the quantum oscillator there is the classically forbidden region so could one say that the forbidden region gives rise to the tunnelling even if maybe you imply that there is tunnelling only when an eigenvalue is outside the trap?
I assume with classically forbidden region you mean the positions of the harmonic oscillator where the potential energy is classically higher than the total energy, so a classical particle could never be there. Yes, in the quantum oscillator the wave function is not exactly zero in this region, it has exponentially falling tails that reach into this region, as can be seen in this picture: http://en.wikipedia.org/wiki/File:Aufenthaltswahrscheinlichkeit_harmonischer_Oszillator.png
This kind of exponential “leaking” is exactly what is going on in tunneling. It is just that for the ideal harmonic oscillator, the “energy trap” is infinitely deep, so in this case there is no tunneling out of the trap. If the energy barrier is of finite height and width, the exponential falloff is also there, but then there is a remaining non-zero amplitude of the wave function continuing on the other side of the barrier.
Just keep in mind that tunneling is a much more general phenomenon and does not necessarily have to happen in space, there are more abstract cases of tunneling.
Crystal clear, thank you very much.
So there seems to be a relation between this oscillatory tunneling and the wave function spreading as a consequence of the uncertainty principle.
See also this answer on stackexchange: http://physics.stackexchange.com/a/54220/31807
So are you saying that quantum jitter doesn’t exist unless we try to examine the position or momentum? Matt, do you agree with that statement?
The question is to Edwin Steiner.
“Quantum jitter” is a metaphor for the fact that position and (conjugated) momentum – and similar pairs of conjugated observables – cannot have well-defined sharp values at the same time. It is deeply rooted in the mathematical structure of quantum mechanics (to be more definite: in the non-commutativity of the mathematical operators representing the observables, and consequently in the Uncertainty Relation) and applies generally, whether you make a measurement or let a quantum state evolve undisturbed. Of course it affects your results when you do measure, and then it really becomes visible as a kind of jitter or noise in your results.
My point was just that quantum jitter is not motion in the sense of things (e.g. average position) changing with time.
I concur.
The jittery behaviour is a consequence of the Uncertainty Principle, and you must try to measure both the position and the momentum, and not either the position or the momentum (which you can do, and will find no jittery behaviour)
I agree up to the first comma. I do not agree with the rest: For example, if you prepare a harmonic oscillator in its ground state, measure only its position, and repeat the whole experiment many times, you would get a series of noisy, “jittery” position values, even if you do the measurement with the theoretically perfect accuracy. The same applies if you would only measure the momentum, respectively.
If my questions sound dumb, I’m sorry, but I remembering hearing that there are no dumb questions only dumb answers, or wait, maybe that was the other way around.
Could tunneling be related in anyway to the supposed foaminess of Space Time?
I’m not sure which kind of relation you want to imply. If your question is: Could tunneling be due to the supposed foaminess of spacetime? – then the answer is definitely: No. There are no fancy spacetime properties needed for tunneling. You can see tunneling in very simple models of quantum mechanical systems which use a completely vanilla picture of continuous space and time (just normal real Cartesian coordinates). For example see the Wikipedia page (it even has animations!): http://en.wikipedia.org/wiki/Quantum_tunnelling
It’s as if that ripple, in the electron field, representing the electron flattens out and since it is jittering, can pop up in another position? Jittering in my mind being unstable in position.
The jitter is the consequence of the uncertainty principle.
To be able to describe the kinematics and the dynamics of a body, we need to be able to determine without a doubt both the position of the body as a function of time and the momentum of of the body as a function of time.
Due to the uncertainty principle, we cannot do that with particles, that is, to determine at the same time without much doubt (inprecision) the position and the momentum of the particle.
We can determine without much doubt (without inprecision) the position of a particle, but not the momentum, or determine without a doubt the momentum of a particle, but not the position.
So, the best we can do to the describe a particle is to say that it jitters.
If a particle, due to quantum tunneling, is able to “appear” beyond the wall, is something that is not directly related to the quantum jitter, but let´s bear in mind that in QFT everything is somehow related to everything else.
I thought that all particles are in constant motion, meaning never at rest. This motion in relation to itself would not be the same as quantum jittering?
In quantum mechanics you need to carefully define what you call “motion”. What is usually meant by “motion” is that a particle first has an average position x and some time later it has a different average position y. In that case we could say that the particle has “moved from x to y”.
What is called “quantum jitter” in the article is not motion in that sense. For example, take the ground state of the electron in the bowl. The ground state is a state of definite (lowest) energy and does not change at all. Neither the average position nor any other measurable average quantity changes in time in this state. Still: If you repeatedly put the electron in the ground state and then measure either its position or its velocity (actually momentum), you would find that most of the time the electron is not exactly at the center, or is not exactly standing still. But keep in mind that your measurement at the same time destroys the ground state and puts the electron in an eigenstate of the quantity you are measuring! (That’s why I said you have to repeatedly put it back into the ground state to do this experiment.) If the electron were a classical particle – which we know it isn’t – we would conclude from these measurements that it is jittering around. For a quantum particle, however, the jitter is to be understood only metaphorically.
Nice article, thanks! About the comment “the electron is tunneling across empty space. If the electron in question came from the barrier, where did the first one go?”, I have a question. Photons, like electrons (and any other particle) are “two-faced” (both wave and “particle”). I have read in several places that when photons pass through (e.g.) glass, they are really absorbed/re-emitted. If this is so, “where did the first one go”? Similarly, if an electron in the ground state absorbs a photon (absorbs the photon’s energy?), the electron may jump” to a “higher” (more excited, not stable) “orbit,” and if that electron later emits a photon (spontaneously), by giving up that energy (of the emitted photon) it “falls back” to the ground state “orbit” (stable). The reason I bring this up is that I have also read that in this “jumping/falling back” process, the electron has never been observed to “exist” anywhere between the two orbits, i.e., it “disappears” from one orbit, and (simultaneously?) “appears” in the next.
Finally, my question: Could it be said that the electron “tunnels” from one orbit to the next, and if so, is it proper to talk about the electron that “disappears” as being “the same” as the electron that appears in a higher/lower orbit? Like the photon being emitted when the electron “falls back” (or causing the electron to fall back because a quantum of energy was given up to form the photon), is it “the same” photon that was absorbed earlier, or is it a “new” photon?
Regarding the transitions between orbits: The key point to understand is that the different orbits – more precisely the states of well-defined energy – form a complete set of states, i.e. a basis. This means that any possible state of the electron can be expressed as a superposition of possible “orbits”. So in order to change from one well-defined energy to another, the electron never has to “leave” the space spanned by the states of well-defined energy. This is not something intuitive, it can only be understood within the mathematical framework of quantum mechanics. Loosely speaking the electron state “rotates” between two states of well-defined energy, in between being in a superpositions of states of different energy.
As for observing the electron “in between”: You have to be precise about what exactly you observe. If you measure the energy of the electron, you will always get one of the energy values corresponding to a state of well-defined energy, never something in between. If you observe the position of the electron, you can find it (almost) anywhere, but then it will not be in a state of well-defined energy. By measuring its position precisely, you have modified the state of the electron significantly, at then it makes no longer sense to speak of “orbits”.
To address your final question: No, there is no tunneling involved when an electron changes for example from an excited state to the ground state – or vice versa. I think your confusion lies here: Because there is a gap in the possible energies, you assume that there is somehow a “gap” between the two orbits that the electron has to “jump across”. There isn’t. The best picture of two states corresponding to different well-defined energies is the picture of two directions at right angles. This has nothing to do with right angles in usual space, it is about orthogonality in the totally abstract space of quantum states. Just as you can smoothly rotate from facing north to facing west, the electron state can smoothly morph from one definite energy to another definite energy. In between it does not have a definite energy. No “jumping” needed at all.
I should add that the electron by itself actually cannot get from one energy to another. States of definite energy are eternal and do not change. If you take the radiation field into account, however, what looked like an eternal electron state before is no longer exactly eternal and can smoothly change into a state where the electron has different energy. In this process the radiation field provides or extracts exactly the amount of energy that is needed to keep the total energy of constant.
In the microscope you show the direction of path from the surface to the microscope tip. Is that indicative that tunnelling is driven by conservation of a certain variable, energy / momentum and/or curvature of space?
Are the ripples following a predetermined space of equal values?
As I said in the text, it’s the choice of setting the voltage on the tip higher than the voltage on the surface; that raises the energy for the electrons in the surface a bit relative to the energy of electrons in the tip, and that attracts the electrons more strongly to the tip than to the surface. I might have tried to explain that better, actually, now that I think about it.
Sorry, but not clear yet. So, it is the electric field and/or magnetic field that drive the direction? Which way would they go if they are just on the “null” point, purely random? I don’t know how to frame the question, could tunnelling be a part of the mechanism that initiated quantum fluctuations or the reverse quantum fluctuations cause tunnelling. in my mind the later would indicate that the curvatures of space is driving fields and hence the ripples. Is why I asked about the BICEP observation, regions of zero polarization could be plane waves (“ground state” of space) the ripples of space cause bosonic fields and so on to heavy atoms.
Hence, energy is a function of space and indeed the theory of nothingness is possible, since space could eventually go back to plane spherical waves.
Wish I had taken that math scholarship instead of fooling around with nuts and bolts. I apologies Professor MacKenzie, 🙂
A voltage difference leads to an electric field between tip and surface — not strong enough to drag the electrons actually into the air gap, but enough that they will preferentially want to tunnel from surface to tip rather than tip to surface. [You could do it the other way, too, running the electrons in the opposite direction; it wouldn’t matter.]
Thank you. Btw, you don’t believe a fermion is a point mass do you? isn’t more like a swirling flux of energy confined by its own angular momentum which is spinning faster than c?
As a chemist, I can assure everyone that certain phenomena would be near impossible to explain but for the invoking of quantum tunneling. The explanation I have always thought explained it was that the quantum jiggle was associated with a wave function, and when the wave function strikes the barrier, there is a finite probability of transmission unless the barrier provides infinite resistance, in which case there is total reflection, i.e. tunneling is a wave property. Maybe that is naive? The second point that a chemist would say is that an electron turns up on the other side, but it does not necessarily have to be the same electron – it could have come from the barrier, which in turn will have taken the first electron, so the question whether the electron can be found in the barrier is not necessarily applicable. Again, naive?
In the case of the two traps (figure 4) the electron is tunneling across empty space. If the electron in question came from the barrier, where did the first one go?
We could put a muon on one side of a wall made from ordinary matter. It can tunnel through to the other side. The muon on the other side can’t have come from the wall, because the wall doesn’t have any muons in it. Moreover, the first muon can’t disappear inside the wall; there’s nothing in the wall for it to annihilate with. So that obviously can’t work.
Moreover, as we’ll see shortly, entire regions of the universe can tunnel from one phase (not one *place*) to another. The barrier, in this case, is an energy barrier that isn’t located anywhere in ordinary space; it’s in the configuration space of the fields of the universe. I can assure you that we’re not losing one universe somewhere in the configuration space of fields and gaining another one somewhere else… especially since the region that tunnels is separated from the rest of the universe by another, physical wall that goes rushing outward. It’s clearly just one universe, with different parts in different phases… much like bubbles of steam inside of water.
All of this is to say that the electron really tunnels. It doesn’t disappear into the barrier, with a second one reappearing outside.
It is true that one can use a wave function to describe the electron in quantum mechanics, though this is not really the way it works in quantum field theory. Tunneling is a general phenomenon; the specific way that it is described in quantum mechanics, using a wave function method, is not really carried over into quantum field theory, even though the phenomenon of tunneling occurs there too. So there’s nothing wrong with your way of thinking about it using wave functions, but it’s best not to lock your thinking about the physics of tunneling to the specific methodology of quantum mechanics wave functions. The physics is that the electron is not a well-localized object, and if a barrier doesn’t require infinite energy to cross, then the electron has some probability of crossing it.
Clearly, the approach of Quantum Mechanics as it was developed in the 1920s is a good “first approximation” that can explain many aspects of particles and fields, but it does offer a picture as complete as QFT.
One of the most relevant successes of the QM approach was the explanation of radioactive decay done by George Gamow in the late 1920s and it is based in quantum tunneling.
But this explanation is also a “first approximation”, since the Standard Model offers a much better and more complete explanation of this process.
I meant to say ” but it does NOT offer a picture as complete as QFT”.
Sorry!
Hello Matt. Thanks for another informative article. Your articles are very helpful and I am learning a great deal from them.
I have a specific question relating to the difference between how things work in quantum mechanics and how they work in quantum field theory. In QM we were taught that the wave function does not have a physical interpretation but the square of the wave function does. Specifically, the square of the wave function represents the probability of finding a particle in a given region of space. Consequently, the amplitude of the wave function is not named and has no units. My question is, in QFT is this also the case or do you have names and units for field amplitudes? My understanding from your articles is that in QFT, the field is considered physically real and not just a mathematical tool. If that is the case, what do you call the amplitude of the field at any given location and what are its units. In classical electrodynamics, the amplitude of an electric field at a point is called the electric potential at that point and it is measured in units of volts. In QFT does the electron field have “electron potential” and if so, what are its units? Thanks.
Fair enough re the muon example. In fact there are examples in chemistry that can only be explained where protons tunnel, and it is clear that the proton disappeared from one side of a barrier and reappeared on the other, and takes an electron with it. What I was suggesting, though, is if the barrier was material, since electrons are indistinguishable, you cannot be sure the electron that turns up is the same electron, and has not exchanged with another. I was under the understanding (wrong?) that all one calculates is the probability of an electron being on one or the other side of the barrier, and there is no label on the electron.
Meanwhile, I look forward to what we shall see shortly. Your posts are very interesting.
There is no possible “labeling” of electrons, they are indistinguishable from each other (all quantum particles are indistiguishable from each other!). This is exactly what Satyendra Nath Bose bumped into while trying to demonstrate the “wrong” black body radiation equation during a class: he made a “mistake” that allowed him to deduce the Planck formula.
He later realized what the “mistake” was: indistinguishable particles! The probabilistic considerations are different, and that will give you different combinatorics, with a different result.
Another nice article, Matt.
I’d just like to point out that our very existence, in a cosmic sense, depends on quantum tunneling; the proton-proton fusion reaction in stars is strongly inhibited by the electric repulsion of the protons, and without tunneling, the reactions rates would be much much smaller and essentially non existent in our sun. (The reaction rate is, of course, also highly dependent upon the weak force, which requires the two protons to be very close for the weak force to work.) Other reaction processes in stars are not quite as simple as the p-p, but all depend on tunneling through electric ‘Coulomb barrier’.
Thanks for that important reminder. I’ll make sure to cover that someday.
My comment is that the quantum marble behaves differently from its classical counterparty already in the first case of a single bowl.
What happens with two of them looks like a direct consequence.
But for this comparison to make sense you should show why you’re choosing the marble instead of a wave to represent the particle…
Is the uncertainty principle a little like taking a picture of a baseball in flight, you can’t know from the picture where it came from, its speed or momentum or where it’s going? The picture gives only a snapshot of a baseball and its relative position at the time the picture was taken and nothing else.
No, it results from the fact that particles aren’t like baseballs. They’re ripples, only partially localized.
The simplest approach that involves “simpler” mathematics and physics is describing a particle with waves.
You have to use Fourier Analysis to do such a thing, and you end up with a wave packet that represents the particle.
That wave packet offers many interesting quantum mechanical aspects of the particle, like the fact that it is not a very well localized object (the waves that sum up into the wave packet are “distributed” over space and time, even though they present a “lump” where the particle is moving).
The wave packet also gives clear evidence of the uncertainty principle: in the “first approximation” to the uncertainty principle that QM offers, it is a natural consequence of Fourier Analysis.
Kind regards, GEN
As I understand it, and not that it is correct, an electron is more like a piece of fuzz. Is this related to jitter?
The problem is that in certain circumstances you need to think of it as a point; in others, as a wave; in others, as fuzzed out. There’s no one image of anything you’re used to that correctly represents the way electrons (or other particles) behave.
Prof. Strassler, I think it is not really correct when you write “And you’ll never catch the electron in the wall”. If you consider the wave function corresponding to the electron, it would be small but non-zero inside the “wall” and you can interpret the wave function (well, the square of its modulus etc., you know what I am talking about) in terms of the probability to find the electron there. So I would say catching the electron “in the act” is possible, although the probability is typically small, so you need some luck to make it.
Anyway, since this is my first post after following your blog for a long time, I feel obliged to say: many many tanks for the wonderful job you are doing here!
But of course, to make the measurement finding the electron in the wall, you’d have to add quite a lot of energy to the system — thereby changing it dramatically. So the problem is that your statement, while formally true, is experimentally never observed. Energy conservation requires that if you make a gentle, careful, low-energy measurement looking for the electron, you’ll find it only where energy conservation allows it — in one trap or the other. The only way to find it inside the barrier is to try to whack it.
I don’t know why it should be considered weird that electrons (and other particles) jiggle and that sometimes electrons are jostled out of their confinement place. Since, as I’m told, there is about a billion photons for every proton and electron it seems to me that as protons and neutrons are far more massive than either electrons or photons that protons and neutrons must act as a sort of shield/aggregator for the electrons due to the photon field and that electrons hang around the well of protons and neutrons because of the mass shielding effect. The electron jitter is just the result of being bombarded by the photon field. Moving (tunneling) an electron to a different atom could just be the result of a higher energy photon, or combination of photons, coming along to kick the electron out of its shielding well and into the shielding well of another.
Perhaps you can tell me why the above, or which part of it, is naive and why?
Vincent, it was good to read your comment! the interesting picture you provided. I was wondering something similar about the jiggle.
Of course it can only be a partial picture to explain things. Still to be explained would be the reason for the difference between neutrons and protons and why electrons behave differently around each type of nucleon. And then to try to explain the experimental results of probing into the nucleon with such a picture. Nevertheless, I like the picture because it is easy to get ones head around and avoids fuzzy thinking and is in line with the kind of forthright logic that led Democritus to argue for the existence of atoms by way of the logic of their needing to be hard little bits and relatively empty space to explain motion and interaction.
“Nevertheless, I like the picture because..”
Yes, I quite agree with you! on this.
There are a few problems with that; firstly the amount of ‘energy jitter’ needed for tunneling to work is far greater than that we observe. The second is that electrons *are* affected by the jitters in the photon (and other) field in ways that have nothing to do with tunneling and we can model this and our predictions agree immensely well. Finally protons can tunnel as can atoms or photons themselves.
Nice article Matt. IMHO one gets a very different sense of it when you pursue the wave-like nature of the electron, particular when you appreciate that the photon really does take many paths. You say the electron’s field is what it is, and it doesn’t have an edge. I think a hurricane is a nice analogy for this. You have a hurricane 100 miles wide and a bowl or trap 50 miles wide. The eye of the storm is in the middle of the bowl, but that isn’t what the hurricane is.
As the tip of the STM “steals” electrons from the surface being scanned, this must leave some of the atoms on that surface ionised… is this effect ever considered destructive to the surface–can it leave it significantly changed (if it’s thin enough; if you scan it for long enough, close enough etc.)?
There is no ‘stealing of electrons’; in reality there are ‘extra’ electrons on the tip being supplied by the voltage. These are repelled by the other extra electrons and would be much more ‘comfortable’ on the surface. As fast as the electrons leave the tip they are replaced by more until the voltage is removed.
The surface however is often heavily altered. For one only a conducting surface will do, anything nonconducting must be covered in a thin layer of metal or charge will build up near the tip distorting everything. Secondly it must be under a vacuum. These two conditions mean that if you want atomic detail it must be of metal atoms (Notice the gold surface above, not say, carbon.) while organic samples can often be heavily damaged just by preparation.
hey, thanks for the clear explanation.
Matt has described in some other posts that it is frequent in Physics to use equations that describe artificial worlds that help us with grasping a better understanding of how the equations behave, and on most situations, these artificial worlds have equations that at the same time, are easier to tackle than the equations for the real world, and at the same time, they gives us a lot of insights about the equations of the real world.
The equations for well potentials that can realistically model atoms are a little bit difficult to tackle with, so, in undergraduate Physics courses it is common to use simple square well potentials to get a better grasp of quantum mechanics.
In many of these simple square well potential scenarios, quantum tunneling is very clear and easy to discover and explore.
Kind regards, GEN
Good point!
A stable, persistent, resonant disturbance in a field.
Resonance is a distinctive and important property to describe a particle in this way.
Thanks a lot for clearing my mistake!
mmm, particles are the manifestation of a certain field, but that is not the same as saying that particles “are” fields.
There is an electron field, which is unique, and there are electrons, that are not unique, they are all identical and cannot be differentiated from each other: electrons are the result of quantum jitter of the electron field.
Kind regards, GEN
No, Gaston, I would not say “electrons are the result of quantum jitter of the electron field”. That is mixing up both terminology and concepts.
Jitter is quantum fluctuations. I have written about them here: http://profmattstrassler.com/articles-and-posts/particle-physics-basics/quantum-fluctuations-and-their-energy/ They are very short lived disturbances in fields.
An electron is a long-lived, well-behaved ripple in the electron field, with a well-defined [rest] mass. It is a stable, resonant disturbance in a field, a very special one, and very different from general jitter.
An analogy: if you have a guitar string, the fact that the guitar string isn’t at absolute zero temperature means it will jiggle a tiny bit, in random ways. If you had a very powerful ear, you could hear this jiggling as white noise. But if you pluck the string, it will vibrate at its resonant frequency, for a long time. You hear this as a pure tone. Quantum jitter is white noise; an electron in an electron field is a pure tone.
The same is true for any field, and its particle.
Is quantum tunnelling caused by quantum entanglement? “Spooky action-at-a-distance” … Albert Einstein
It was Einstein, after thought experiments with his colleagues Boris Podolsky and Nathan Rosen, who outlined that quantum theory applied not only to single atoms (and the fundamental particles that make up the “atom”) but also to molecules made of many atoms. His rational was a molecule containing two atoms could also be described by a single mathematical expression, a wave function. So, Einstein realised that if you separated these atoms, even by a vast distance, they would still be described by the same wave function. In the jargon, they were “entangled”, as if their fate was connected in some way.
Hence, if “everything” follows the same theory, as described by the quantum wave function then the traps are two solutions, eigenvalues for the “electron field” hence the electron can pop up in any one of those two “spaces”. Which one could be driven by, simply , chaos (what you call quantum jitter), purely random.
I understand the math, covered Fourier transforms in college, but I still cannot grasp what is creating all these fields (space at different energy levels)? Yes, if there is one space then “everything” that exist in that space is “riding” the same wave and hence “entangled” but, what is twist and stretching and oscillating this space?
What is “space”? Do we live in a 3D world because our world’s solution is 6 quarks or did the 6 quarks create the 3D space. i.e. the cartesian coordinates are defined the “average” alignment of 6 quark’s “centers” in the atomic space.
Are there two types of spaces one which existed before the quantum jitter (inflation) and our 3D space which is defined by the 6 quark solution (and one electron to balance the quantum jitter in the atom).
My intuitive imagination tells me, Energy ~ F(space).
No, it’s really not an entanglement effect. I would have said so if it were.
Does “no” mean that the fundamental particles, like that electron, are “closed” fields? And these closed fields can “ride” on open fields, like the EMF?
I get that but, could these closed fields be tightly wrapped spaces all curled up in the continuum of one space and one field?
‘Entanglement’ in sense it is used in QM involves two or more ‘particles’; waves within a field. Tunneling involves only one particle at a time. Tunneling can be considered as a result of the wave nature of particles however; an electron which is a perturbation of the EMF does not have a precise location, its wave extends as far as the EMF itself. (With some caveats.) When we measure the electron then there is a large probability it will be in the first trap but also a small probability it will be in another trap, that probability rapidly falling off to zero as the distance between traps increases. The electron hasn’t moved between the traps; in one (inaccurate) sense if we haven’t just observed it it could be in both traps.
“… an electron which is a perturbation of the EMF…” I question the validity of the statement, I hope the good professor could verify it. But I hope your are correct!, 🙂 I’ll explain why.
Also, you write ” … When we measure the electron then there is a large probability it will be in the first trap but also a small probability it will be in another trap, that probability rapidly falling off to zero as the distance between traps increases.”
I really hope this is correct, so for the skepticism but our measuring techniques are not very good, as we saw with the FTL neutrinos, 🙂
So what to make of this? Symmetry, perturbations, fields, waves, fermions, bosons, tunnelling and all the rest of the concept we have formulated thus far, what is the common feature(s) which can be factored out of these ideas?
Energy and Space … and I dare say you may even be able to reduce this to just one by saying … Energy ≅ Space.
So how can a single entity create such a magnificent universe? We don’t know why perturbations occurred but we do know that energy tends to one direction, to the ground state. One variable, one law and the rest are derived from this simple mechanism. If you can accept energy and space are one then you can visualize what a singularity could be, a isotropic state of all the energy (space) that make up our universe. Energy is the property of curved space much like a compressed spring.
So for me an electron, fermion, is a curled up volume (3D space) created by an initial condition which is common to all electrons and stable because it is trapped (closed), it requires a much higher energy to undo it (open it from the tight curvatures). Much like a knot on a rope, if you pull on both sides the rope will break before the knot is released.
We (fermions) are all curled up 3D spaces (6 quark solution) in a single medium of space continuum. i wish one day I can visualize what caused the perturbations.
Here is another question that may have an answer, recently BICEP detected the possible gravity waves via the polarization pattern of the earliest photons. In the same “light” are there any patches of zero polarization (plane waves)?
Thanks for this informative article Professor. I heard tunneling in the avenger movie, they were discussing about stabilizing the quantum tunneling effect to lessen the energy required to break through the coulomb barrier. But now I see tunneling is about the uncertainty principle so stabilizing it is impossible.. I mix up science and fiction some of the time and I appreciate that you’re here to explain, thanks! 🙂
Single orbital (non hybridized orbitals), like S, P, D and F (the first four orbitals that correspond with the first four levels of energy) are symmetrical orbitals, but they are not gaussian distributions.
Besides, the gaussian distribution is one of a few distributions that is not skewed (it is symmetrical and not slanted to one side), and so, for the gaussian or normal distribution, the three parameters of position, the mean, the mode and the mean, the all share the very same numerical value, so, in the gaussian distribution, there is no numerical difference between the average value, the most likely value and the middle value.
Kind regards, GEN
“This is called, poetically, “tunneling” — but you should not imagine that the electron digs a hole through the wall. And you’ll never catch the electron in the wall.”
Intuitively, your statement sounds right. but is it really the case? How do you know the electron can never be in the wall?
What are the methods used to verify this experimentally and theoretically?
Intuitively, sound(=vibration in the filed made of atoms etc.) can penetrate a solid wall without digging a hole, so maybe an electron (vibration in another field? made of what?) can penetrate a different wall in the similar manner if this wall can conduct “all the vibrations” necessary to reconstruct the electron in another side of the wall. Is this how the tunneling works in a way?
“The closer are the tip and surface, the more easily electrons can tunnel across the gap.”
Sure, but how do you know the electrons are really “tunneling” instead of just traveling/flowing across the gap? Electrons can just flow without tunneling, can’t they? Can you distinguish the two in this condition? Why do you need to introduce “tunneling” in explaining the (change in) electron flow in STM?
“Quantum `jitter’ is ultimately responsible for this remarkable possibility.”
->why? Because without Quantum `jitter’ nothing can occur? What exactly is the mechanistic connection between tunneling and quantum jitter at the most fundamental level?
The answers to your questions all boil down to: experiments, and a theoretical tool derived from those experiments which is used to predict the results of many other experiments.
We can observe electrons moving across barriers that, were the electron to go through the barrier the way you and I are used to, would require more energy than the electron has available. In particular, in the STM, the “wall” is just the air gap outside the surface of the material under study. The electrons do not have enough energy to leave the surface of the material under study and wander off into the air. If they did have enough energy, they’d just leave the surface on their own, without the need for the microscope tip! [This energy can be measured using the photo-electric effect, whose explanation won Einstein the Nobel Prize.] The electrons stay in the surface unless the tip is very close to the surface… but there is no need for the surface and tip to touch. Instead — even though no energy has been added, and the electrons still do not have the energy needed to exit the surface — they end up moving out of the surface and appearing in the tip, generating an electric current.
Why should you trust our understanding? Because although my article is qualitative and descriptive, our understanding is quantitative and predictive. The STM wasn’t designed by accident! And getting the shape of the surface out also doesn’t occur by accident. Calculations, based on the mathematics of quantum mechanics which underlies our understanding and interpretation of our experiments, play a role.
To say this another way: we use the mathematics of quantum mechanics and experiment in synch. We know from many experiments that tunneling appears to occur. We have equations of quantum mechanics that purport to describe this phenomenon. Why do we believe these equations? Because they make precise quantitative predictions for how tunneling (and other phenomena) occur — not just vague qualitative predictions — and these predictions agree with precise experiments.
Using our equations, we know how to calculate what would happen in a world where quantum jitter was smaller, or even absent. And one can easily see in those equations that when you turn off quantum jitter, you also turn off tunneling. There are wave-like aspects to electrons, which are part and parcel of this quantum jitter; and these wave-like aspects are responsible for tunneling. If electrons weren’t wave-like in this respect, they would not — could not — tunnel.
Q1)You did not explain why the electron cannot be in the wall. You said “you’ll never catch the electron in the wall” (because electron wave attenuates sharply inside the wall?) but If you wait long enough, can you occasionally or monetarily find it in the wall (or gap in the case of STM)? I guess it will not stay in the wall/barrier/gap long as it seems very unstable energetically/potentially. But the electron wave does seep into the wall/barrier/gap, right? The electron wave does exist inside the barrier during crossing and then appears in the other side, correct? “”not”” like apparation/teleportation etc. (=jump from point A to B “without traveling” the distance/wall/barrier between) correct?
Q2)”The electrons stay in the surface unless the tip is very close to the surface..”
I think the distance from the tip to the sample is extremely small in STM. So, it lowers the energetic potential barrier and does not require much energy for an electron to move from one side to the other. And if “quantum jitter” is, in a way, similar to Brownian motion(or thermal jitter), an electron can occasionally(and for a very short period of time? which is consistent because only very short time is required to cross a very small gap.) gain higher kinetic energy than their collective average like an molecule/atom in gas/liquid can sometimes gain higher energy (but not high enough to break off the surface if the tip is not close enough). maybe this can explain the behavior of the electrons in STM? If so, why do you need to introduce something called “tunneling”?
Can you present a physical phenomenon in the way that it does not make sense or cannot be explained without “tunneling”? What is the difference between a “tunneling” electron and a “traveling” electron? Their wave patterns (wave function pattern) are different according to each condition? that is all? everything else the same?
“Using our equations, we know how to calculate what would happen in a world where quantum jitter was smaller, or even absent. And one can easily see in those equations that when you turn off quantum jitter, you also turn off tunneling.”
Examples? I guess it will affect if(or how much) an electron will travel straight or spread out after coming out of a small hole if quantum jitter is small or absent but how does quantum jitter affect tunneling?
As for “Why should you trust .., a role. To say this another way: .. precise experiments.”
So I heard many times but hammering this into people’s head again and again does not help them understand the phenomenon.
In stead, please explain/show a few concrete examples with graphical simulations/representations of an electron wave passing a wall (by theory) and how this matches (or deviates from) observed experimental data (or better yet manifests in observable familiar phenomena). List what can happen and cannot happen as the consequence of or during tunneling, and explain why so.
I’m sorry, but if you want such technical detail, you’re going to have to pay for a private tutor. Seriously. I just can’t take the time to “show a few concrete examples with graphical simulations” etc.; that would take many hours of my time, on a subject that is not central to this website. If I were to do things like that it would bankrupt me pretty quickly, so I’m sorry, but I’ve gone as far as I can go in this direction. I don’t blame you for wanting more, but I suggest that you should take a quantum mechanics class, if you’re prepared to do the math, or that you pay for a smart graduate student at a university to spend the hours required to show you how this stuff works.
I will answer your first question. You will never find the electron in the wall because its presence there would fail to conserve energy — unless you do an experiment that adds enough energy to the system, in which case you *can* find it. But of course, in doing so, you’ve changed the tunneling situation by giving the electron enough energy to go *over* the barrier. Is that confusing? Of course it is; at this point you need the math or very careful explanations with lots of pretty animations. It’s beyond what I can do here.
Sure. Please do what you can as you feel comfortable and not, of course, to the extent that bankrupts you. If you could come up with another relatively simple way to deepen the understanding of and explain the phenomenon in a way that address some of my questions, please do post it, I will appreciate/find it interesting. It might do good to other readers too.
Thanks for this part “unless you do an experiment that adds enough energy to the system, in which case you *can* find it. But of course, in doing so, you’ve changed the tunneling situation by giving the electron enough energy to go *over* the barrier.” as it clarifies things to some extent.
But what I want to know is what is the main/essential difference between A) going *over* the barrier and B) going *through* the barrier(=tunneling?). Sure, A) requires more energy obviously (but must the electron in A) always have shorter wavelength to go “over” the barrier? or this is not the must condition?). but what else is the distinctive difference between A & B? It sounds intuitively strange if nature is doing two different things:it must be essentially doing just one thing (something like what quantum field theory describes) which turn out to look two different descriptions.
“You will never find the electron in the wall because its presence there would fail to conserve energy”
->if the electron can gain kinetic energy from “its surrounding” “for a very short period of time” and use it to cross the barrier, the energy seems to be conserved during the process(but this sounds strange because then the energy on one side is higher than the other and this sounds unlikely to happen. in this case the energy is conserved but entropy seems to be decreased and this cannot happen at least empirically (could such entropy-decreasing process be allowed in quantum field theory with extremely small but nevertheless non-zero probability?). Does quantum field theory have build-in irreversibility of process?). If so, how can going “over” and going “through” the barrier be distinguished? or are they essentially the same process? (though I guess they probably have different wave amplitude/distribution pattern depending on the energy of the electron and the type of barrier)
Could you answer the following part of the questions:”But the electron wave does seep into the wall/barrier/gap, right? The electron wave does exist inside the barrier during crossing and then appears in the other side, correct? “”not”” like apparation/teleportation etc. (=jump from point A to B “without traveling” the distance/wall/barrier between) correct?”
I believe you said in another section of this website that “quantum wave” cannot “jump” (=cannot disappear at point X and reappear at point Y separated by space. This is consistent/obvious intuitively but you did not provide why this is so last time. Is there an explanation for this or it is just accepted as the way it is in quantum field theory?). If this is applicable to an electron crossing a barrier (or tunneling), then the electron always goes “through” the wall regardless of its energy during the process of A) and B). True?
“..you’re going to have to pay for a private tutor.” “..you pay for a smart graduate student ..”
with due respect, Matt, I strongly disagree with you here. Seriously as if everyone can afford to do so.
“I’m sorry, but if you want such technical detail..”
No, I am not sorry, nor do I necessarily want technical details or any other things you are incorrectly guessing, talking, or suggesting improperly that do not directly address/answer my questions. I am pointing out that the information in this page does not seem to be sufficient for one to conclude/confirm “definitively” and “clearly” the existence of tunneling process (=whatever this really is in nature) though the page is a nice introduction (but most of them I have already read/known elsewhere.) and that I want more convincing arguments strongly suggesting that only tunneling model (but no other models) can explain the phenomenon presented here. Do I think tunneling is utter rubbish, and you are talking nonsense? Of course, not. I just want to deepen my understanding of the phenomenon in a way that makes sense to me more than I currently do.
“. You will never find the electron in the wall because its presence there would fail to conserve energy — unless you do an experiment that adds enough energy to the system, in which case you *can* find it. But of course, in doing so, you’ve changed the tunneling situation by giving the electron enough energy to go *over* the barrier.”
Yes, but with a caveat! You don’t have to make the electron go “over” the barrier TO THE OTHER SIDE.
You can make it go “straight up” to another “electronic state”. Picture three bowls, the
two you describe plus another one held above them, centered between them. You can aim
photons at the two lower ones and make the electron go to the upper one … while its in the middle
of the two lower ones … and only there. (Technically this is called a “Franck-Condon factor”.)
And in the real world, sometimes the electron can flow out of the upper bowl without tunneling
down a slide, and do work in the process, or the system can emit a photon and so the
electron ends up in yet a fourth bowl, centered under the third one.
This experiment can learn about the nature of the area between the two original bowls.
It’s how you learn about the nature of the barrier. This is very important in chemistry,
where there are dozens of other “dimensions” to the picture.
Maybe trying too many kids to physics is not a good idea after all? 🙂
Apollo and space shuttle programs attracted so many kids into engineering that it created a generation, maybe two, of really bad engineers. We bad crops for years and we are paying it now with runaway budgets due to poor performance. Both the Challenger and Columbia catastrophic failures were due to systemic problems, a technical way of saying bad crops of engineers.
How many more thousands of useless theories will too many poor physicists create causing so much delays and mistrust with the people paying the bills for the much needed big experiments that have yet to be funded?
The physics faculty should proceed with invitations only, allowing in only the best of the best, then you will see real progress.
There are several ‘essential differences’ between ‘climbing’ and ‘tunneling’. The first is that it is relatively easy to detect something that is climbing a barrier; if you add energy to the STM electrons so they can just jump the gap then I can fire particles at them and knock them out as they move through that gap, detecting them. I can take measurements of them as they pass through the vacuum, there’s no ‘trouble’ detecting them. But in the case of tunneling I cannot do that. The electrons appear to be in one place then be in another without physically moving through the space between.
Another difference is the energy required and how this changes the rate; as I add energy to the electrons the amount of tunneling happening doesn’t really change that much. This is because energy has little to do with tunneling. However climbing is greatly affected. As you note the occasional exceptional electron will jump the gap by getting a higher-than-average amount of energy. as the average energy rises the amount f climbing increases rapidly and continues to do so after the average energy exceeds the amount needed for an electron to jump the gap.
Tunneling by contrast is also highly directional; when electrons have enough energy to leave the surface it tends no matter how far the tip is from the surface; electrons will leave the tip at a given rate though not all may reach the surface. But tunneling is exponentially dependent on distance which doesn’t make sense for climbing. (In many cases of climbing we’re dealing with particles in a bowl getting out of it rather than going from one bowl to another; the electrons can climb out of the tip to any point in space but they can only tunnel to the surface.)
Both processes often occur together, the overall rate being a combination of the two.
In regards to the electron wave, this is actually a fundamental part of tunneling. It’s not so much that an electron is a marble moving about but rather its position and speed are not precisely defined. We can think of the ‘marble wave’ as being spread out across the whole bowl and beyond. In some sense the marble is already in the second bowl though it has a very low chance of being found there. We can imagine observing the marble repeatedly. Most often we will see it somewhere in the first bowl near the bottom. We cannot observe it between bowls since that would violate conservation of energy but there is a tiny chance that we will see it in the second bowl.
“The electrons appear to be in one place then be in another without physically moving through the space between”
This sounds quite contrary to how Matt explained quantum wave in another page. If what Mat says is correct, your statement here is probably wrong. If no “quantum wave” can jump, electron wave cannot jump either and electron wave must be moving (physically? ->whatever this means) through/inside the wall.
@el- I’m no expert, but if you’re sincere in your questions (part of me suspects you’re just anti-quantum theory) I would suggest that your fundamental mistake is in thinking that an electron is something that you can picture in your head and understand. As Matt tries to stress, an electron is like nothing a human brain can picture. No one knows what an electron is doing when it’s not being measured, and in a very real sense it’s meaningless to talk about what an electron is “really” doing. The wave function is not a real wave of anything – it’s an evolving probability wave that at each point in time has solutions that represent the probability of where you’ll measure the electron to be should you make a measurement at that time. Up until the point you actually make a measurement, it’s just a probability function. Thus, an easy way to explain tunneling is that when you solve the wave equation for a given state, there is a tiny but non-zero solution of the wave function that corresponds to the electron being found (as if by magic) in the well of bowl number two. If you make enough measurements, you will eventually find that the electron “tunneled” exactly the number of times your solution predicted (1 in a hundred, 1 in two hundred etc…). No one knows what the electron is “doing” while it’s not being looked at, and as I stated above, it’s not even really a meaningful question.
the last sentence should read – no one knows what an electron is actually “doing” when it’s tunneling, and in a very real sense it’s meaningless to ask. Every time one looks for an electron (i.e. makes a measurement) it is either here or there, but no one knows what it’s doing in between. Only it’s probabilities can be measured.
And it’s never found in the wall because the solution of the wave function that is “in the wall” corresponds to a zero chance of the electron being found there.
ah – better explanation of the wall below – should have known to read all comments first. I’ve just done the simplified wells Gaston refers to (or was it kudzu?).
@andy:”.. I’m no expert..” then, stop making irresponsible statements and wrong assumptions as you do not know what you are talking about. ridiculous.
“Why should you trust our understanding? Because although my article is qualitative and descriptive, our understanding is quantitative and predictive.”
Matt, are you saying that people should trust what you say just because you said so? If so, you are wrong. There should be critical questioning from the people trying to understand the subject and it is completely reasonable, acceptable, desirable and fair. In fact, it should be encouraged. Scientific understanding should never be about swallowing/accepting a comment/dogma blindly from a big figure or rote learning. Stop brandishing your authority, that is the last thing a scientist should do. Of course, many heard QFT predictions match zillions of experiments at a spectacular accuracy. But remember many have no access to fancy expensive gadgets nor required costly resources and cannot verify these experiments. If you can present how to verify QFT predictions experimentally at home with low budget, that would be extremely interesting.
I don’t read Matt’s line as an appeal to authority. I read it as a statement that he can show you all of the steps but he cannot show you all of those steps in a single blog post. I think Matt does a great job building series of blog posts that aim for something above Scientific American but below a real physics education. Not because he doesn’t want you to to learn but because a real education takes years.
Your point about verifying QFT experiments caught my attention. At home the world is mostly classical. That is why classical physics is such a good model.
What is a cheap experiment for seeing quantum mechanics at home? Turn on an electric burner and explain why it turns red. Build a shoebox spectrometer. Look at different lights in the house.
What is a cheap experiment that demonstrates relativity at home? I can’t think of any. You can’t make anything around your house go fast enough to see the effects. If you have a GPS, you are using the results of relativity every day and I suppose you could make an app that simulates how off the location function would be if you turned off the relativistic correction. But that is not verification if you assume the GPS engineers and physicists are conspiring against you.
QFT is the marriage of quantum mechanics and relativity. The simplest example of the effect of QFT that comes to mind is the Lamb shift in the spectrum of hydrogen due to fluctuations in the vacuum of the electromagnetic field. This shift was measured in 1949 and if you really wanted to build the experiment in your garage, I guess you could do it. In terms of equipment it would probably cost less than a new car to set it up.
The key point is not the fix of the gps receivers but the ticking of the atomic clocks on satellites and what is really going on there…
Boring as what you say is nothing new and leads to no concrete experiments nor simple thought experiments to verify QFT’s validity or invalidity. What you say does not add/help much for the people to verify QFT directly. Most of what you say sounds like tautology of what has been circulating around for years. As if the well-informed are not aware of any of them. If you can present simple methods/setup/experiments using what is readily available&cheap such as garbage/trash in dumpsters or at home which verify QFT in the ways that its prediction “inevitably manifests” and “adds up/shows up” in ordinary phenomena observable/measurable in daily scale, that would be interesting but I doubt you can (but if you can, please do so. It would be useful for many.). I do not need any more tautology, history nor other obvious same old things/useless chitchat.
We all know that words are deceiving, so, that is why scientists are very careful with definitions.
It is clear that Matt is describing a probabilistic aspect of the position of particle within the orbital (because of the effect of the uncertainty principle, we have to use a probabilistic description of the position of the particle, and that description is the orbital, since we can’t give a more precise description, like an orbit).
Regarding any kind of statistical distribution (and quantum mechanical orbitals are in themselves a special kind of distribution), there are some important parameters that describe “position”: the mean, the mode and the median.
When Matt describes the “typical” position, he is describing the most often or most likely position, and that clearly is the mode and not the mean. The mean would be the average position.
Kind regards, GEN
I think the statement about “average” vs. “typical” position isn’t as…precise as it could be. For ordinary quantum mechanical systems I’d say that the average position *is* the typical position-just that the probability distrubution of the position has a finite width and, for a “free particle”, average and width define the distribution (since it’s Gaussian). For a particle in a potential this isn’t the case, but the potential is related to the moments of the position and can be reconstructed from them. However, for a fixed, confining potential, the distribution for the position has its maximum at its average value, thus the typical value is the average value.
I agree with Gaston in his comment below; if we use coordinates (x,y,z) with the center of the trap at (0,0,0),
the average location [i.e., if you make many measurements of the electron’s location, the sum of the locations divided by the number of measurements] is at (X,y,z)=(0,0,0), i.e., the center;
while the typical measurement will find the electron at a typical distance from the center [i.e., the most likely value for the distance, the sum of the distances from the center divided by the number of measurements] which is the square root of the average value of (x^2+y^2+z^2), and that is not at zero.
I think Stam is questioning whether I should have been clearer about this. I’m not sure; thinking about it.
Matt, from your answer I see that what you mean by “typical” distance is the standard deviation about the average value;whereas what I mean by “typical” distance is the value of the maximum of the probability distribution of the distance. My reasoning is based on the way these terms are used in disordered systems (and probability theory). In disordered systems it is, often, the case that the average value of a quantity, drawn from a distribution is not at the maximum, because the distribution isn’t symmetric and has a long “tail”–the magnetization of a disordered spin system is a…typical example. In quantum mechanics this isn’t,…typically the case, the dstributions are peaked at their average values, even if they’re not Gaussian. But in quantum systems, with disorder, things are different, e.g. localization of electrons-which is relevant for the discussion of tunneling, when you have barriers, whose width and height vary with the sample. Then the localization length does have a non-trivial distribution, whose average value is different from the typical value.
Stam, the maximum value of the distribution is the mode, again, we are all talking about the mode as the expression of the “typical” value.
Regarding quantum mechanical probability distribution functions (the Born rule), it is not correct to say, as an overall definition, that the distributions “are peaked at their average values, even if they’re not Gaussian”.
For instance, the s orbital is a perfect sphere, so, it has the very same value of probability everywhere, which means that it does not peak at any direction in particular. The average value is zero, as the average value is the barycenter of a sphere, its value is the actual center of the sphere.
For the p orbital, it has 3 lobes pointing towards both directions of the x, y and z axes. So, it has 6 peak values: + Max X, – Max X, + Max Y, – Max Y, + Max Z, – Max Z.
All Max values are identical in modulus: ||+Max X|| == ||-Max X|| == ||+Max Y|| == ||-Max Y|| == ||+Max Z|| == ||-Max Z||.
The average value of the orbital with its 6 peaks is the barycenter of this shape, which again, is the center of coordinates, which means, it is again 0, 0, 0.
Gaston, what things are called isn’t as important as what they mean. That’s why I wanted to stress that what’s physically interesting is whether the value at which the probability distribution attains its maximum value coincides with its average value-or not. In quantum mechanics the answer is Yes. This means that, if one were to run many experiments, numerical or real, the “most probable value” would be the average value–but there would be a non-zero “spread” and, for a free particle all other quantities would determined by these two moments. For an anharmonic oscillator, with a single-well potential, other moments are needed, but the relations between moments allow one to determine the parameters of the potential. And, even for multi-well potentials (with finite barrier width and height), in fact, while the “classical” potential has a maximum between the two wells, so, “classically” it seems as if
the average position *isn’t* the typical position, if one takes into account the quantum fluctuations, one finds that the average value of the position is at the, classical untypical value-but that’s just the result of an incomplete calculation, which illustrates why tunneling is relevant. In quantum field theory, with an infinite number of degrees of freedom, the barrier can become infinitely high and tunneling becomes suppressed-and a phase transition can occur.
Tunneling effects allow many of the magical properties present in solid-state electronics, the kind of electronics behind all kinds of modern computers like in our smart phones, favorite game consoles or tablets.
So, in a sense, the tunneling effect described here is very relevant.
Kind regards, GEN
When and were and how does it matter when electrons tunnel. Can it make a difference? Aren’t they kind of wiggling and changing places all the time?
Here’s just one of thousands of examples of why it can be important in chemistry and biochemistry: http://www.isgtw.org/feature/nature%E2%80%99s-subway-quantum-tunneling-enzymes . There are probably many, many more examples we don’t know about yet.
Yes, electrons (and all other objects too) are subject to quantum jitter all the time; but the fact that the type of jitter in question allows electrons to go through what would naively seem to be impenetrable barriers isn’t obvious to most of us (until we learn the math behind it.) For example, if I just jiggled the red bowl in Figure 2, above, back and forth rhythmically, and just a little bit, that would make the marble move around, but it wouldn’t kick it over into the blue bowl. The details do matter.
Great article!
Just about any article you write points out the fact that to be really able to describe quantum physics, we have to delve into the equations head-on, and work out the details, including the proper interpretation of what the equations mean, and this article in particular is no exception.
What really amazes me with every article is that you have found a useful way to avoid the math mumbo jumbo (at least, on many articles) and describe the main facts with pictures.
Getting back to the concept of quantum tunneling and the equations, we could say a few interesting things about that.
To start with, it is a weird and counter-intuitive concept, but we also know that this is one of those nice mathematical “tricks” that nature has favored.
Regarding the mathematical “trick” in itself, we also know that quantum tunneling is just a “natural” consequence of the general procedure to solve partial differential equations, it naturally emerges out of solving the equation.
When you have a potential well, which in the classical physics realm, objects cannot escape, in a quantum mechanical context, you have those beautiful exponential functions fading out of the well (because these exponential functions have a negative power) and giving the particle a probabilistic path out of the well, thus, the “tunnel” effect.
Kind regards, GEN