By the time Einstein came along with his special theory of relativity in 1905, it had been over 200 years since Newton wrote down his laws of motion. His followers had developed his notions further, elaborating and clarifying them. And two centuries of scientific experiments, of engineering and of technology had been based on these ideas, confirming them directly and indirectly to a very great degree. In all of the life of the 18th and 19th century, Newton’s equations worked. They weren’t likely to stop working in the 20th century, and indeed they didn’t: 19th century clocks, engines, ships, mills, refrigerators, gyroscopes and cannons worked just fine after Einstein’s theory of special relativity appeared in 1905. So how could Einstein “overthrow” Newton? How could Newton have been “wrong”?
It is easy to write a new set of equations and say “I think the conventional equations are wrong and I think my new equations are right.” Anyone can do that. Indeed I get dozens of papers sent to me or mentioned to me every year (by amateur physicists) that say exactly that about Einstein’s equations. But they mostly can be seen to be wrong on the first page, because there’s some experiment or technology that wouldn’t work at all if the new equations were correct. It is extraordinarily difficult to invent equations that are consistent with all previous well-established experiments and technology. Such is the high standard of science, and of nature.
Einstein — and a few of his colleagues — had some clues that some significant changes to theoretical physics might be necessary. In the late 19th century there were two sets of equations (“theories”) being used in physics, for different phenomena. These were Newton’s 17th century equations for how forces cause objects to change their motion (accelerate) and the 19th century equations that govern electricity, magnetism and light, whose complete form was first given by Maxwell, following on the work of Faraday, Ampere, and many others. For phenomena where both sets of equations were needed, one could find situations where the equations led to inconsistent predictions. Knowing that there is an inconsistency is one of the things that allows theoretical physicists to have confidence that they should modify their equations, and can give them a hint as to where that modification might be necessary. But that doesn’t mean finding an acceptable modification is easy.
The trick — and if you think about for a bit, the only possible trick in coming up with new physical theories (and one which, in my experience, very few amateur physicists really appreciate) — is to find equations that extend previous equations, so that it can be proven that in the realms that experiments and technology have already tested, the new equations equal the old equations up to tiny deviations that generally are too small to have yet been noticed in any existing technology and in all (or almost all) previous scientific experiments.
What I’m going to do now is show you how that works for some of Einstein’s equations.
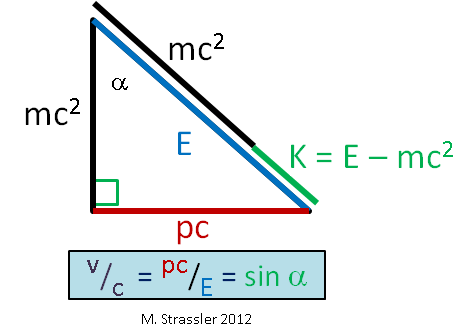
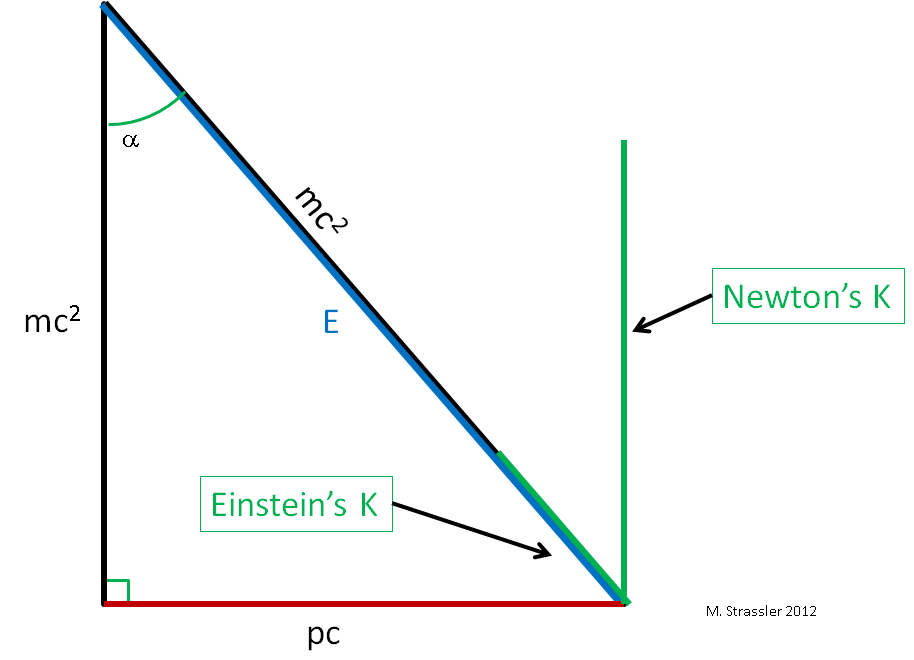
For an object moving freely through empty space, and as viewed by an observer who sees the object moving at a speed v, Einstein proposed relations between energy E, momentum p, mass m and speed v that can be represented through a triangle, as described in detail in this article on mass and energy, and as reproduced more briefly here by the triangle in Figure 1. The energy E is a sum of mass-energy mc2 and motion-energy (which in this article I will call “K”, because the technical term for motion-energy is “kinetic energy”). Einstein‘s equation relating energy and momentum and mass is the Pythagorean relationship
- E2 = ( p c )2 + ( m c2 )2
while the speed v is given by a trigonometric relation
- v / c = p c / E = sin α
(Here and always on this website I define “mass” as a quantity on which all observers agree, sometimes called “invariant mass” to distinguish it from the archaic “relativistic mass”. That is, as in Einstein’s original paper and in his later-in-life viewpoint, mass should be defined so that E = m c2 only for a particle at rest, that is, for a particle with p=0; this invariant mass, unlike relativistic mass and unlike energy, does not increase with speed. I’ll explain why particle physicists take this point of view in an upcoming article.)
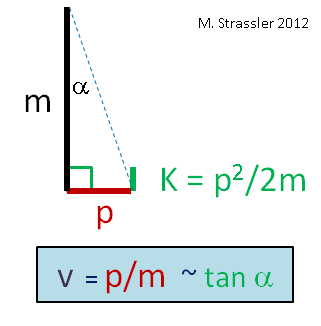
Newton’s equations (and their elaboration by his scientific descendants) have a different set of relations, given by the three line segments shown in Figure 2. Newton and followers did not know about mass-energy — that was something that Einstein proposed (as did at least one other of his colleagues, but only Einstein got the details right). So the only energy they talked about (for an object moving freely) was its motion-energy, (which I’ll call “K”, because the technical term for motion-energy is “kinetic energy”.) Newton and friends also didn’t know about the speed of light. So the pre-Einstein relation between motion-energy K and momentum and mass was
- K = p2 / 2m
while the relation involving speed is
- v = p / m ~ tan α
(When you combine these two relations you get the formula you may be more used to: K = 1/2 m v2.) Now this set of relations is not given by a triangle, but by the three line segments given in Figure 2.
Now how did Einstein manage to get a set of formulas that could agree with all previous experiments? (With all of them!) What’s the trick?
Einstein’s relations are almost identical to Newton’s in the case that an object’s speed is small compared to the speed of light! You can see that in Figure 3. Suppose the triangle has a small angle α, which corresponds to having a speed much less than the speed of light. For Einstein, a particle traveling on its own has motion-energy K equal to its total energy E minus its mass-energy m c2 , as shown in the figure. Notice K is much less than E. Then, as you can see by eye in Figure 3, Newton’s prediction for K and Einstein’s prediction for K are almost the same size; the smaller is the momentum p, the closer the two predictions become. Meanwhile, the formula relating the speed to momentum and mass is almost the same too, because Newton says
- v/c = p/mc = pc / mc2
(in the second equation I put an extra “c” in both the top and bottom of the fraction), while Einstein says
- v/c = pc / E
but these two equations are almost the same when v is small, because mc2 and E are almost the same when v is small. (You can also see this in terms of the angle of the triangle, because tan α and sin α, which are related to Newton’s and Einstein’s formulas for the speed, are almost identical for a small angle.) So Einstein’s Pythagorean relationship, and Newton’s three line segments, are experimentally indistinguishable as long as the speed of an object is very, very small compared to c.
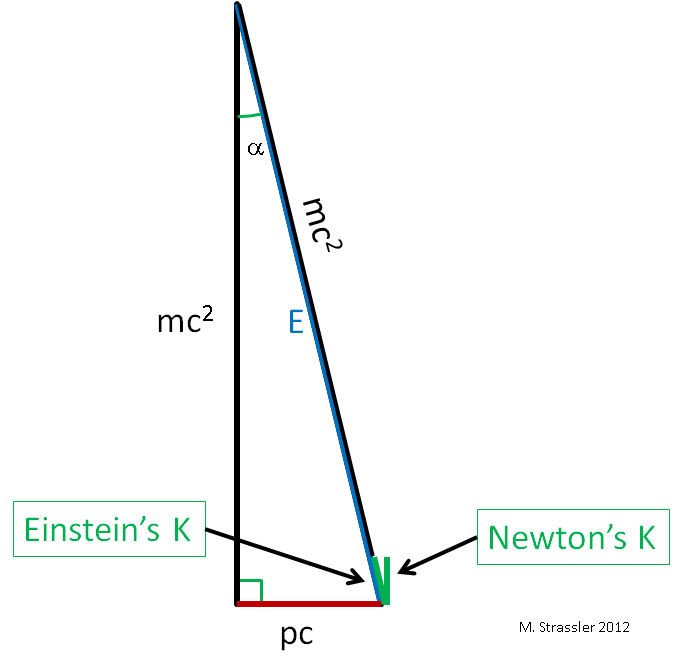
In short, Einstein’s equations are very, very cleverly formed; whenever velocities are small, Einstein’s relations and Newton’s relations are almost indistinguishable. This is why — as Einstein checked himself, before presenting his equations to his colleagues (amateurs, please take note) — all existing scientific experiments and all existing 18th and 19th century technologies were consistent with Newton’s equations. The predictions obtained from Newton’s theoretical framework were and remain correct, for all practical purposes, as long as all velocities of massive objects are slow compared with that of light.
That’s for stuff on the slow side. What about fast stuff?
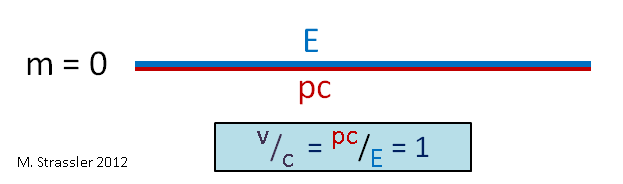
In the 19th century the only objects known that traveled anywhere near the speed of light were electromagnetic waves (including but not limited to visible light.) Those waves were known to have v = c, at least to the accuracy that anyone could measure. But Einstein’s grand and extremely radical proposal was that these waves were actually made from massless quanta (i.e. `particles’ of a sort, called “photons”), which would also satisfy his relations between E, p, m and v. If you put m=0 in Einstein’s equations, the equations still make sense: try it, you’ll find E = p c and v / c = 1 . (See Figure 4.) This is what you would expect for photons — and thus Einstein’s relations work both for ordinary massive objects of daily life and for the massless photons that make up light!
No one could have made Einstein’s proposal before him. Because to propose light was made from massless particles wouldn’t have made any sense. Look at Newton’s equations. If you have an object whose momentum p isn’t zero, and you put m = 0, you get K = infinity and v = infinity! That’s something people already knew experimentally wasn’t true for light. And if instead you take p=0 and m=0, Newton’s equations for K and v are both “0 divided by 0” and thus don’t make any prediction at all.
To summarize, Einstein slipped his proposal in between two things people really knew at the turn of his century. They knew that massive objects obeyed Newton’s equations to very high accuracy up to the speeds of bullets and cannonballs, which though fast are still tiny, tiny fractions of c. They knew that light was made from electromagnetic waves moving at about the speed c. Einstein, in suggesting that light was made from massless photons and that Newton’s laws for massive objects needed to be extended to a set of equations that could govern both massive and massless particles, was a great unifier. And through this unification he made a prediction: that massive objects moving close to the speed of light would not obey Newton’s equations, but his own.
Since experimental techniques weren’t instantly available to check what Einstein was proposing, and the proposal was so radical, there was a lot of pushback initially from people who thought what he was proposing made no sense. But already some parts of his relations were tested between 1908 and 1920. And it didn’t stop there. Technology and scientific technique have come a long, long, long way since then. Many 20th and 21st century experiments and technologies access much higher velocities than were possible in 1905; indeed particle physics experiments and their medical applications depend crucially on particles with speed v comparable to c, as does our detailed understanding of atoms. And for such particles, Newton and Einstein’s equations disagree sharply! This is shown in Figure 5. All measurements done on fast particles agree with Einstein’s formulas, and not Newton’s. The debate is long over (except at the inevitable fringes.) Even the Global Positioning Satellite (GPS) system depends on using Einstein’s equations, instead of Newton’s.
Someday we may find situations in which Einstein’s equations don’t work, and themselves need to be extended. Maybe our first hints will come from an experiment. Or maybe they will arise through the recognition of a theoretical inconsistency. But so far, the special relativity equations that Einstein proposed to govern E, p, m and v, for objects moving freely on their own — and the speed limit that those equations encode, that no object can be measured by any observer to be traveling at a speed faster than c — are still operating without any conflicts.


69 Responses
Clear article, thanks.
I am just an engineer with limited physics knowledge and good mathematical background and…I am very happy I found this page! Thank you
Should the note for Figure 4 state that the vertical/black/mc2-only side collapses? If so, then I still get why you wrote “has no horizontal side” as soacahtoa drawings are normally laid out rotated 90° counter-clockwise as to how you laid yours out, but again I see why you laid it out the way you did for this illustration.
Friends total solar eclipse never ever happened on earth yet because at constant distance moon is far smaller than earth so its always partial or small part of earth can see the sun totally blocked by moon. My observation implies the parity of movements between sun and moon at endless wobbles of earth where solstice minima and maxima was established, if sun is at northern hemisphere moon is at southern hemisphere of earth and there is a point when they aligned causes what we called total solar eclipse at particular place on earth. Because moon never rotates nor revolves around earth at fix gravitational attraction phases of moon is determined by its position higher or lower than earth. Total solar eclipse happens when moon passage with the sun aligned to earth and blocks it physically. Total solar eclipse is a physical obstruction of the moon like a small marble at 1 meter distance totally blocked a basketball at 100 meter distance from the focal point of your very own eyes if by chances moon never passes higher or lower than earth. I have demonstrated it and figured out in my book titled SOCIAL ANIMATION.
Gaddemit ladies and gentlemen, ALL THAT YOU KNOW IS WRONG, Light never travels at all, it is linoums or shinning particles in the space which move or align to energy source.which forms a beam of light towards the source of energy. SUNLIGHT NEVER COMES FROM THE SUN BUT TOWARDS THE SUN. Sources of light is always a vacuum energy like open flame, bulbs or flashlight, once lit or energized shining linoums aligned towards it as light we see. Please refer to my book written 1994 about it, demonstration and theories are there, titled CHAOTIC TRANSITION, by SIMON ROS my pen name AKA.
One more thing, this theory of relativity is obsolete, null and void because whole universe is at fix gravitational attraction like planet earth and moon, Moon never rotates nor revolves around earth, it is fix to see the rabbit image everywhere and everytime on earth. The back or far side of moon was seen for the first time during the survey of landing site for apollo 11 while the far side of the sun was seen only last Feb 06 2011 after sending STEREO behind it. One week, one month or one year never ever happened eversince at fix gravitational attraction planet earth never revolves around the sun independently but revolves with the sun as a dot in a rotating shaft. Our Roman calendar is highly erratic, September must be 7th month while December as 10th and last month but we still celebrates New year on January after assumed 365 days by innocence and folly. Please share this truth to others, I am tired of writing books to inform the public.
I was reading War and Peace and notice this paragraph ” but momentum (the measurement of motion) is the product of mass and velocity.
Could Albert Einstein have read this particular paragraph and develop his idea from it ?.
Leo Tolstoy seem to have been a great mathematician besides being a writer
Now know,, what is exactly the theory.
This site looks like a website that is worth studying indeed. I have almost no education at all concerning the works of Galileo nor Newton ( Don’t ask why, but my parents pulled me out of school before I had a chance to receive any education in physics.). However, I was always interested in motion, and I had noticed something odd about motion that no one else seemed to be concerned about. I eventually found the answer, and at the same time had independently discovered the effects described via STR, and I had independently derived the STR equations, including the Lorentz transformation equations. My method of deriving these seems to be 100% unique, and thus is found nowhere else.
https://www.youtube.com/watch?v=KKAwpEetJ-Q&list=PL3zkZRUI2IyBFAowlUivFbeBh-Mq7HdoQ
Well I am heading on over to your “NEW? START HERE” section.
A friend of mine and I argued this evening about data. I theorized that Einstein, in some form, had data to base his observations and theories on. His point of view was, no the Genius of Einstein was he created these ideas in his mind without the benefit of data . Any particular point of view on this argument ?
absolutely interesting!! Wlady
Helpful information. Fortunate me I discovered your web
site accidentally, and I’m shocked why thi twist of fate did not took place earlier!
I bookmarked it.
Are there any plans to write an article on the AdS/CFT correspondence?
A very brillant man thanks 4 da help
Pretty! This has been a really wonderful article. Many thanks for supplying this information.
Meen eqution of eisteen c
I studied your triangle diagram and I believe it could use some clarification to help show that v cannot exceed c. The problem is that none of the sides are labeled v or c, instead they are labeled pc, mc2 and E.
Of course, the mathematically inclined may make the effort to deduce, from your equations, that pc could stand for v, and E could stand for c, but I think you’ll agree that this is far from obvious.
It might be sufficient to add v and c, parenthetically, to pc and E.
I am glad there are those of you who write in regard to this complicated subject. As a retired simpleton lawyer all of this is over my head as far as math is concerned so you are probably going to tell me to shutup, but I am a practical person and that is why I am writing. As I understand your field, you are theoretical physicist with the main word being “theoretical”, and I will admit all of you are better at math than I am. What I don’t understand is what is the practical use of theoretical physics. Tell me how it is used other than just being mind thought principals. Explain to me how these theories are used to accomplish something. For example Gravity has always interested me and I have been reading for a hour about what Gravity is and the math to compute it and I see the benefit in putting satellites around the earth but things I don’t understand is why for example we are interested in finding other planets that can sustain life. So what. They have discovered some planets they think could sustain life and they are 500 million light years away. Who cares. We can’t even talk to them. In fact the closest star is out of our range to visit. OK so they claim there may be a worm hole. Another theory. Educational I will admit but I want to see the practical use. It also amazes me that you all know that Atoms are made up of electrons, protons, neutrons,etc. yet you can’t see them so how do you really know they are there. Maybe I am wrong because I just had proton radiation from the proton found in the Hydrogen atom and a machine was designed to extract that proton from the Hydrogen atom and cure my cancer. Now I see the practical use of that so I guess you scientist will tell me I am all wet. It’s interesting to tell me that gravity is why the planets travel around the sun in an elliptical path and that we can’t live on any planet or moon in our solar system. My answer to that is that is all interesting but why do I care. We went to the moon but what return did we get. We want to go to Mars, and I say why? We can’t live there and we will gain nothing but knowledge at a great expense. Sorry guys, I am not putting you down, I just want to know the practical side of it.E=mc2 allowed us to create atomic energy. I am not sure it accomplished anything other than warn us of the danger of radiation. That equation also puzzles me. How did Einstein know that you could take mass and multiply that times the speed of light squared and get Energy. Since you guys say you can’t exceed the speed of light then how in the world can you square something you can’t exceed. sydhorn@gmail.com Syd Horn
Your means of explaining the whole thing in this
piece of writing is in fact pleasant, all be capable of easily be aware of it, Thanks a lot.
I want to modify my comments regarding mass and momentum because as I look at the diagram again, the author has surely adopted the common (but regrettable) practice of letting c =1, thus m becomes mc. otherwise, you are welcome to use it.
I think I see a problem with your figure 2 where one leg is momentum, a vector, and the other leg is mass, a scalar. From this you deduced an angle alpha. This immediately raises the problem of how to scale the paper for p (=mv) and m so as to make sense. I don’t see an easy way to do it. In my opinion such a triangle is invalid.
Furthermore you assert that K =p2/2m was the pre-Einstein relation between momentum and mass, showing that there is a way to get the usual 1/2mv2 from K.
Actually the correct sequence would be derivation of 1/2mv2 from Newton’s equations, and then if you let p =mv, you can arrive at p2/2m.
The derivation: W = Int m (dv/dt) (dx = vdt) = Int mvdv =mc2/2.
Also in that figure you show a short segment called K = p2/2m that is foreign to the rest of the figure.
But congratulations on making a wonderful effort to lay out these details.
Correct. I noticed that as well.
Matt, Thank you for all the work you put into these articles + the much greater work you seem to put into responding to the comments.
When you say that the triangle relationship shows that the speed of any massless particle must always be c, are you only referring to the speed of that massless particle in a vacuum?
For example does a photon travel through water at c/1.3?
Or is at always moving with velocity c but every so often it hits a water molecule and gets absorbed and then later re-emitted with the average of the time lost is these absorb/emit interactions c-c/1.3?
You said in this article that “Newton and friends also didn’t know about the speed of light.” but it seems that they actually knew about “the (finite) speed of light” from “Rømer’s determination of the speed of light [1]” but did not incorporate it into the framework of the physics at that time.
1. http://en.wikipedia.org/wiki/R%C3%B8mer%27s_determination_of_the_speed_of_light
thanks. your website definitely deserves an award. this page being a typical example of its superb quality
duncan
you mention you get many crackpot ideas who bleive they can overturn einstein’s equations, but fall over very quickly. would you be able to give 2 or 3 illustrated examples with equations. (not too lengthy)
thanks
I’ll try to do that sometime; it has to be in a context that won’t offend an individual.
These triangle arguments to visualize how Einstein s special relativity smoothly passes into Newton s equations for small enough velocities is so beautiful (as the whole article is), I`ve not seen this presented like this before :-).
It is amazing how Prof. Strassler can generate these nice amazing posts faster than I can keep up reading them, even though he has so much important and urgent things for the LHC to do.
After reading this article I just felt like saying thanks again for this very nice site … 🙂
Hi Matt.
I do not agree, that “techniques weren’t instantly available to check what Einstein was proposing”. There were at least one check instantly available and I think Einstein did it: Perihelion precession of Mercury. The STR explained a large part of the unexplained part of this (the rest is explained by GR).
Professor, thank you for this elaboration on the model using the right triangle. When I saw how “faster than light” makes no sense, modelled on the triangle, things became much clearer to me.
I think Einstein was obsessed with the inconsistency in Faraday’s law and the Lorentz force being seen as different effects which he mentions at the beginning of his 1905 paper. That he had succeeded in showing they were the same phenomena but seen in different frames must have been one of the key reasons behind his confidence in his theory.
He derives kinetic energy in his 1905 paper, and the total energy in a later paper, but I don’t recall him mentioning relativistic momentum. I think Plank did this when defining relativistic force shortly after.
I wonder how much of special theory of relativity is contained in works of Lorentz. Shouldn’t be Einstein’s equations named after Lorentz?
Lorentz certainly was a great scientist and deserves some signficant credit for having guessed some of the right mathematical equations. He (and previously FitzGerald) suggested that moving physical objects changed their sizes in a clever way, which we now, in his honor, call Lorentz (or FitzGerald-Lorentz) contraction. But he did not have the right concepts behind his equations; he didn’t have the whole package. And getting the whole package required a huge conceptual leap that Einstein, with the fresh eyes of a young man and an exceptional level of genius, was able to make. Not that this was immediately obvious to everyone at the time!
I’ve seen this happen, on a smaller scale, in my own career. One of the big developments in my field during the late 1990s is what we now call the AdS/CFT or field-theory/string-theory correspondance. There were many hints of such a thing going back to the 70s, and the work of ‘t Hooft. Many others played with it over the coming decades but couldn’t make it work in a clear way. Polyakov was heading in the right direction quite a few years ago; he figured out key elements of the idea. People like Klebanov and Gubser got many of the right equations in the mid-to-late 90s. These people are all terrific physicists and their names will be remembered, certainly within string theory. But it was Maldacena who managed to think it through, got the point, put all of it together, and in late 1997 made the final, giant conceptual and mathematical step. What he figured out (and what others, following his insight, figured out) changed the subject forever and impacted many subfields of high-energy physics. For this he is justifiably famous.
That sounds like an interesting story for those of us not familiar with string theory (or Maldacena). I’d love to see a more detailed retelling.
Jep, I’d love to see more too 🙂
Could someone explain to me how we define momentum for massless objects? Isn’t it the case that in classical dynamics that if m=0, p=mv=0, and so E=0? That is to say, massless objects have no momentum or kinetic energy?
Multiplying mv by the Lorentz factor doesn’t change this result, does it? So how does an object with no invariant mass hha have a defined momentum?
Your equations and/or your concepts are off, that’s why you’re confused.
Caution — enormous confusion is created by some textbooks and public articles by the use of `m’ to represent both what I call `mass’ (and some call `rest mass’ or `invariant mass’) and the separate quantity E/c2 (which I call `energy divided by a constant’, but others call `relativistic mass’.) On this website I only use `m’ to represent the first quantity. That is the definition used in modern particle physics, to avoid confusions such as yours.
And with that definition, p = m v is not correct in Einstein’s theory. Read my article on mass and energy, http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/mass-and-energy/ , for the correct equations, which are more complex to write down, but are easily visualized using a triangle.
If you use the other definition of m (where m is relativistic mass = E / c2 then you’re led to the ugly conclusion that since all particles (including photons) have energy, all particles (including photons!!) have mass. This is not where you want to end up, conceptually.
Energy is a property of matter. To say it exists without matter is something an English major would write. “Beams of pure energy”. Remember the mass of a photon is relativistic. The rest mass is small.
http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/matter-and-energy-a-false-dichotomy/
Almost right. Einstein and Newton forgot about vector energy mcV, the real law of Gravitation is :
Ehttp://wp.me/wweC= -mGM/r + mcV = -mu/r + cmV Quaternion Energy, with cmV=cP the vector energy aka “Dark Energy”. Newton’s deflection is tan alpha=.5gt2/R where R = 150Gm and g= earth gravity 9.8 and t= R/c.
see my Blog.
I get comments like yours at least once a day. You want to be the next Einstein, but you’re tossing concepts around without understanding them, as though you think Einstein didn’t understand every element of the physics of his time, backwards and forwards. Let’s just see where you’re coming from. Your formula contradicts Einstein’s general relativity. Have you checked that your formula gives the correct perihelion shift for Mercury AND the correct time shift for the Global Positioning Satellite system AND the correct slow-down rate for the Hulse-Taylor pulsar? Because if you haven’t, why are you wasting our time?
Nice article Matt. I am looking forward to see the extension of
E/p = C (For a massless particle)
In the next paradigm shift. Do you have any proposal ?
No.
In this case Kaluza\Klein then had such a process and a structural basis in Einstein’s Equations?
“Einstein’s position, however, gradually changed. From about 1919 onwards, he took a strong interest in the unification programme3. In later years, after about 1926, he hoped that he would and a particular classical unified field theory that could undercut quantum theory. Such a theory would have to contain the material objects -sources and fields- and their dynamics. He would even expect the distinction between these concepts to fade: \a complete field theory knows only fields and not the concepts of particle and motion” [?]. We will study how he wanted to realize these principles in classical Kaluza-Klein theory, and try to see what his objectives and results were.See: Einstein and the Kaluza-Klein particle – http://cdsweb.cern.ch/record/466266/files/0009087.pdf