© Matt Strassler [August 29, 2012]
This is article 3 in the sequence entitled Fields and Particles: with Math. Here is the previous article.
Once we’ve understood the equations for an oscillator — which describe pretty much everything that bounces or wiggles or rolls back and forth, such as a ball on a spring — we can move on to learn about something equally common in nature: waves. Waves are everywhere: sound and light, the rolling motion of earthquakes, ripples on the surface of a pond, etc.
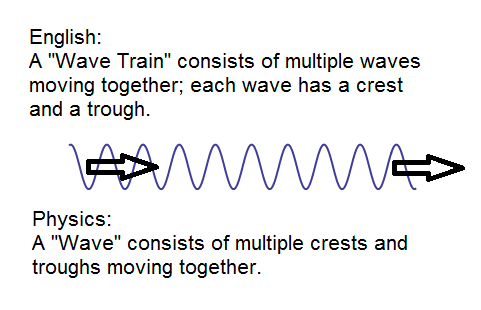
Before we start, a caution: the term “a wave” can be confusing, because what it means in physics isn’t what it means in English. In physics, it doesn’t mean what we often, in English, would call a wave at the ocean’s edge — a single crest and trough. Instead, what “wave” often means in physics is what we might colloquially in English (or in physics too) call a “wave train”: a series of crests and troughs all moving together in the same direction with the same speed. The simplest form of wave would be one where all the crests are the same height and the same distance apart, and we’ll focus our attention on this case.
Waves are truly remarkable things, once you start to think about them. Imagine you and a friend take a long rope and stretch it rather tightly across a room (Figure 2). Then imagine your friend moves one end of the rope (the green end) up and down a few times. A wave will form at his end of the rope, and it will travel across the room (click the figure to animate it) to your end (the red end.)
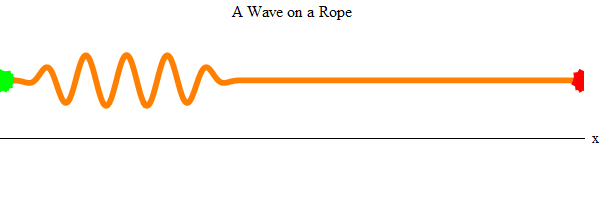
This is amazing. I mean, really: amazing, profound, and crucial to everything in our universe, including you. Look at what has happened. No physical object has moved from left to right — at the beginning, before your friend shakes the rope, the rope is stretched across the room, and at the end, after your own end of the rope shakes and the wave is gone, the rope is still stretched across the room exactly as before. And yet! Energy, and information, has moved across the room. The wave, as it travels, is carrying the energy that your friend expended when he shook the rope — and carrying the information, in its shape, about how many times and how quickly he shook it — to you, where it made your hand shake, and (in this case — though not true for all waves) it even shook your hand the same number of times and in the same pattern. Wow! No physical object moved across the room, but still, energy and information did.
Or wait. Should we think of the wave as a physical object? Just as physical as the rope?
With that extraordinarily deep question in mind (and if its profundity isn’t clear to you yet, do not fear — it will be soon enough) let’s now turn to the little bit of math we need to describe what a wave looks like and how it behaves, and then the slightly more math we need to write down the equations whose solutions are waves. This is analogous to what we did for the classical ball on the spring; if you haven’t read that article recently you may wish to review it.
A Formula for an Infinite Wave at a Specific Time
The reason this set of articles goes directly from the subject of a ball on a spring — an oscillator — to the topic of waves is this: a wave is sort of double oscillator — oscillating both in time and in space. We’ll refer to time using the variable “t”, and space using “x”.
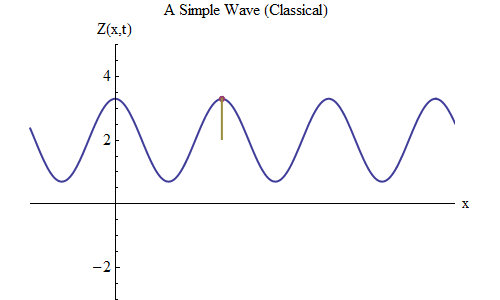
Look at Figure 3 below. It illustrates a wave that extends on in both directions for a great distance, with a huge number of crests and troughs. This is a bit different from the wave we saw in Figure 2, which only had a few crests and troughs. The difference is inconsequential: in Figure 2 I was interested in illustrating something for which the precise shape of the wave didn’t matter; but now we’re going to focus on the math formula for waves, and that’s a lot simpler for waves that have a huge number of equal-height crests and troughs. And this case will also turn out to be very useful for understanding how quantum mechanics changes how waves behave.
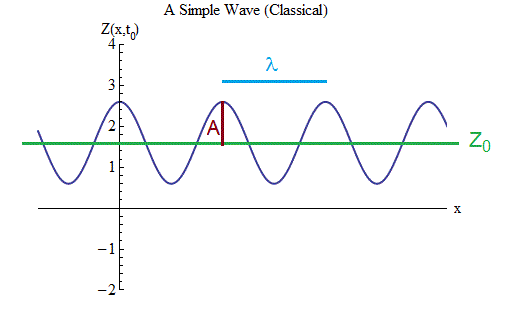
If you click on Figure 3, it will show you an animation of the wave moving to the right — all the crests and troughs moving together.
Our first task is to define some language and write a formula that describes the motion and shape of the wave in Figure 3, just as we did for the ball on the spring.
If you don’t click on Figure 3, so you just look at the static, unanimated figure, you notice that I’ve labeled a few things on the plot.
The plot shows the size of the wave Z as a function of space, at a particular value of time, t=t0: we write this as Z(x,t0). As one traces it across space, it oscillates back and forth, with Z increasing and decreasing repeatedly; at any fixed time, it is an oscillator in space.
Note that Z may or may not itself be related to a physical distance; it might be something like the height of a rope, as in Figure 2, or it might be something rather different, such as the temperature of the air at a certain point in space and time, or the orientation of a magnetic atom at a certain location inside a magnet. But x really does represent a physical distance, and t is really time.
The snapshot of the wave, Z(x,t0) has three interesting properties, the first two of which are shared by the ball on the spring.
- First, there is the equilibrium value Z0, which lies halfway between the largest value of Z at each crest and the smallest value of Z at each trough. (Most of the time we’ll just study waves with Z0 = 0, because often the value of Z0 is unimportant — but not always.)
- Next, there is the amplitude A, the change in Z from its equilibrium value to the top of each crest, or (it’s the same) the change in Z from its equilibrium value to the bottom of each trough.
- Finally there’s the wavelength of the wave — the distance λ between adjacent crests, or (it’s the same) between adjacent troughs, or (it’s the same) twice the distance between each crest and the adjacent trough. This characterizes the back and forth wiggling in space, just the way the period (=1/frequency) characterized the back and forth wiggling in time of the ball on a spring.
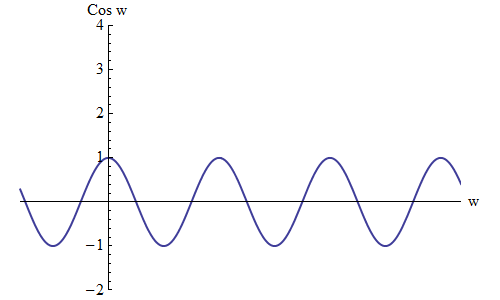
Now, what does the shape shown in Figure 3 look like? It looks like the graph of a sine or cosine function; see Figure 4, where cos(w) [that is, cosine of the number w] is graphed versus w. Now cos(w), is an oscillating function that clearly has equilibrium position at zero, amplitude 1, and wavelength 2π. How do we go from Figure 4 to a formula for the wave in Figure 3? First we multiply cos(w) by A to make the amplitude equal to A; then we add Z0 to the whole thing to shift to the correct the equilibrium value (so that if A = 0 there’s no wave and the whole thing sits at Z=Z0); and finally we replace w with 2πx/λ, because cos w has crests at w=0 and w=2π , so cos 2πx/λ has crests at x = 0 and x = λ. Altogether this gives us
- Z(x,t0) = Z0 + A cos (2π x/λ)
This is almost the same formula that describes how a ball on a spring bounces in time, which was z(t) = z0 + A cos (2π ν t) = z0 + A cos (2π t / T), where ν is the frequency of oscillation and T = 1/ν is the period of oscillation. You see the analogy: Period is to time as wavelength is to space.
Let me make one last remark before we go on. I could just as well have written
- Z(x,t0) = Z0 + A cos (-2π x/λ)
That’s because cos[w] = cos[-w] . The fact that we are free to put a minus sign into the formula for the shape of the wave in Figure 3 will be important later.
A Formula for an Infinite Wave at a Specific Position
Now let’s ask a different question: let’s look at how the wave changes in time, but follow a particular point on the rope, to see where it goes and how it moves. This is shown in Figure 5; you see that I’ve circled a particular point x0 that happens to be at a crest at time t0, and if you click on Figure 5 you’ll see an animation that both shows the wave as it moves to the right and also follows the size of the wave Z at the point x0 as it varies in time: Z(x0,t). And you’ll immediately observe that the height of the wave at this particular point behaves just like a ball bouncing on a spring! And it therefore has the same formula as a ball on a spring, as a function of the frequency ν of the wave, or the period T = 1/ν, where T is the time between the moment when the wave at x0 is a crest and the moment when it is next at a crest, after being at a trough just once.
- Z(x0,t) = Z0 + A cos (2π ν t) = Z0 + A cos (2π t / T)
[I’ve written it both in terms of frequency and in terms of period because physicists usually use frequency, but the period is more similar to the wavelength, so you may prefer that. Either way is fine.]
The Complete Formula for the Infinite Wave
Now we need a formula for Z(x,t), which describes the wave that we saw in Figures 3 and 5 (or any similar wave) at all points x at all times t. And the right answer is
- Z(x,t) = Z0 + A cos (2π [ν t – x/λ]) = Z0 + A cos (2π [t/T – x/λ])
which incorporates both of our formulas for a fixed point in time and for a fixed point in space.
One thing to notice is the minus sign that appears in front of x. I mentioned earlier that we were free to put a minus sign into our formula for Z(x,t0). With a minus sign in front of x and a plus sign in front of t, the formula describes a wave moving to the right, as in the animations in Figures 3 and 5. To see this, note that when t/T – x/λ = 0, the wave is at a crest, because cos[0]=1. So at t=0, there’s a crest at x=0; but if t moves forward a bit, say to T/10, then there’s now a crest at x = λ/10, a little bit to the right of where it was at t=0 — so therefore the crest (along with the rest of the wave) is moving to the right.
What would be different if we put a plus sign instead of a minus sign into our formula for Z(x,t)? Well then there would be a crest at t/T + x/λ = 0, so in that case, at the time t = T/10, there would then be a crest at x = -λ/10, a little bit to the left of where it was at t=0 — and so now the wave is moving to the left (Figure 6).
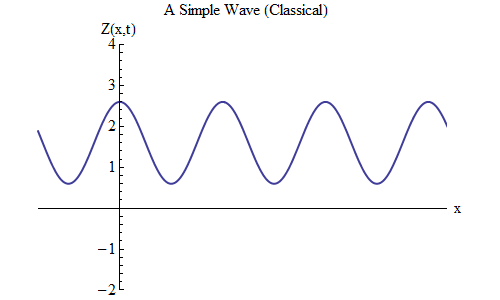
Waves that are functions of x and t can move in either direction, so we just have to choose the right formula for the given wave. More generally, when we work with waves that can move not just along one spatial direction x but in any of our our three coordinates x, y and z, then those waves can move in any direction, and we have to choose the right formula based on the direction that the wave is moving.
Fine point: we could also put a minus sign in front of t instead of in front of x. But +t, +x is the same as -t, -x, because that’s the same as multiplying the whole formula inside the cosine by a minus sign, and cos[w]=cos[-w]. So +t, +x and -t, -x both give a wave that moves to the left, and +t, -x and -t, +x both give a wave that moves to the right.
Equation of Motion for Waves
Now, just as for the ball on the spring, where we first figured out the formula for the oscillatory motion of the ball, and then looked at the equation of motion for which that formula was a solution, we want to do the same here. We’ve found a formula for the shape and motion of a wave. What equation of motion has such a formula among its solutions? Click here for the next article.


8 Responses
Matt, I think it is very valuable that you keep rephrasing (re: waves) “This is amazing. I mean, really: amazing, profound, and crucial to everything in our universe, including you.” I keep thinking that a wave/field requires a physical medium. I think it does most of the time, but its important to realize that physicists might have a hard time with that too. In Grigory’s description of a rope whose molecules are tugging at their neighbors, that physical analogy, while a good starting point, fools me in to thinking that a wave always requires elements of a medium to move. But it’s such a good analogy! Air pressure waves are a good analogy too. The comparison to an oscillator requires an equilibrium and I’m asking if there is an analogy that doesn’t require the movement of physical particles (as if your job isn’t hard enough!).
The ball-on-spring analogy says that potential and kinetic energy keep shifting back and forth. Because energy is conserved, this would oscillate forever with no degradation. The rope wave analogy says that the energy is moving along the wave without degradation too. Macroscopically, we know a force is needed to move a mass across a distance. So is it incredibly amazing that a wave can propagate energy through space without degradation? It would seem some energy is needed to perform the propagation. Can you explain why not?
In the rope analogy, assume both ends are tied to a tree. When you pull the rope up to snap it, the point you’re pulling requires energy to displace from equilibrium. But all the points from that pulled point to an equilibrium requires some energy too. Consider a steel cable vs a rope. The same displacement requires different amounts of energy. So it would seem each kind of field has a different “tension” that determines what amplitude occurs for the same energy input. Since the energy propagates without energy loss, it would not matter when two fields intersect what the amplitude of the waves are, just the energy. Is this true, or would the amplitude of the wave in the field have other affects?
Dear prof. Strassler! Thank you very much for your work! I’ve just found this site, and feel inspired by the new brush strokes in the picture of the world it gives :). However, I can not catch this particular article, and it leaves me distressed :).
The example with a bouncing ball was straightforward: we took an intuitive physical process, we examined the forces which influenced the ball, and recovered the equation that describes the position of the ball. Thus we got the _process_ we called an ‘oscillating motion’, the ball we called ‘oscillator’.
This article started with another intuitive example: a stretched rope and another physical process which starts with shaking one rope end. And there my personal intuition broke. Instead of finding out what and why would happen to a rope, we just stated that the _wave_ (not the rope! as with the ball!) is a ‘double oscillator’: the term that evades me. The term ‘oscillating both in time and in space’ also misled my understanding: oscillation of the ball ment it repeated the position over time.
What _is_ a wave altogether? How and why does the wave ‘move’, if it does altogether? The wave on the rope is bound to move along the rope axis, what about the wave (a wavelet? a single ripple?) of a single photon? Shall it move in a single direction (where sent), or in all directions, as ripples on the water surface?
Ok — I see various points of confusion here. If your intuition is letting you down here, buy a “Slinky” or a long piece of string, and try this yourself!! It will help you build your intuition to see real physical materials acting as I have described.
What is doing the oscillating? As you say, it is the ball in one case, and the specific locations of the rope in the other. I probably misspoke to say it was the “wave”, but I need to reread the article carefully to see if I did this poorly. In the end, it is the wave we are interested in, not the rope. Because it is the wave that will travel across the room, carrying information and energy — not the rope, which in the end did not go anywhere.
Regarding the term “double oscillator”: as the wave moves along the rope, a given point on the rope goes up and down — oscillating, just like the ball on the spring. Is this not clear from Figure 5? You can see that there is oscillation across time by watching a particular point on the rope as it goes up and down — and you can see there is oscillation across space by looking at the shape of the rope at any given moment. This oscillation in both time and space is what makes it “double”.
Now, what is the rope doing? and what is the wave doing? Notice they are two different things. The wave is moving sideways as well as up and down. The rope is only moving up and down. This is the truly fascinating part about waves! If we look only at one point on the rope, it appears to be just like the ball on a spring. If we look across the rope, however, we see its shape is also oscillatory — which is something beyond the ball-and-spring example.
You asked: what determines where the wave goes? The answer is that it depends how it was started. If you wiggle the left hand edge of the rope, the wave can only move to the right — there isn’t any rope to the left. If you wiggle the right-hand edge, the wave will move to the left. But if you wiggle the middle of the rope a wave will move in both directions! More generally, a light bulb will send light in all directions, unless you place it against an opaque wall. A flashlight sends out light in a beam, but that’s because all other directions are blocked off by opaque material and mirrors.
I’m sorry, I wasn’t clear enough. Of course I do not need the rope to predict how it behaves, that kind of simple everyday sort of intuition is shared by most. It is the flow of your explanation, which attracts me most, and which was broken here. And the meaning of words, of course. Forgive me, if i’m sort of wasting your time, but it’s part of my job to create unbroken convincing explanations, and that is why I’m trying to figure all that out.
So, we had a ball on a spring. We tried to push it and saw it had started (due to the forces of the spring) going back and forth. It became an oscillator: it started oscillating over time, that means it’s position *repeated periodically* over time. We could have even noticed its position formed a cosine curve, it gave us an insight on the answer, but only an insight. We asked ourselves why it behaved like that, written down the equations of forces and obtained a solution, which indeed was a cosine.
Now we have a rope: the whole collection of molecules, with adjacent ones being connected to each other with intermolecular forces. We tried to push it and saw:
1) Specific points started going up and down: their height positions repeated over time (just as if it was a small ball from the first example);
2) Heights of points repeated over space: that’s a second repeation involved, though no point of the rope indeed oscillates along the rope (moves back and forth along the rope as ball on a spring).
Thus every point oscillates only up and down, and the heights of all the molecules of the rope *repeat both over time and across space*. That is where the term “double oscillation” doesn’t really fit the everyday intuition: A naive understanding of oscillation is something going back and forth.
The question is: how we can produce the equation for a rope, just as we have produced them for a ball? The following intuition may help: every point on the rope tugs its neighbors. The force on some point of a rope depends on relative positions of adjacent points. Thus how fast the point oscillates over time depends on its current position and on how strong its neighbors pull it: d2Z/dt2 ~ Co * Z + Cx * d2Z/dx2. Or the other way round: How strong the point pulls its neighbors depends on its position and on how fast it moves itself: d2Z/dx2 ~ Co * Z + Ct * d2Z/dt2.
Then we may try to solve these equations and draw the cosine of both time and distance formula and indeed it will fit wat we observe on our rope.
Is that a more or less correct understanding?
Yes, that’s basically right.
I do not see how the football stadium analogy can provide answers to the required conditions for a (physics) wave to propagate. A human wave can be produced with transmission of information (energy) or without (in case each person moves up and down periodically without communicating with each other). When with transmission, it occurs because each person can influence the next (by voice, sight, or touch etc.) but it does not say how/why each person can influence/transmit anything to the next one:i.e. how all the fundamental forces can influence anything at a distance (or how energy(wave) can propagate from point A to B). It feels magical yet real and ordinary like the conservation of energy. I can see/feel(observe) it happen but that’s about it for now. I do not know how nature/universe keeps track of energy/charge or (how all the conserved quantities are (or not) connected or emerge) etc. it just happens. but does not necessarily mean that is the end of the story (for example, the exact connection between mass and energy was not clear until Einstein revealed it.). BTW, when you say “a lattice” are you talking about something like a lattice made of atoms? Or a lattice is like those crystal models:each ball connected with rigid sticks to the next balls repeating the same pattern in 3D? But a lattice (model) is continuous in the sense that the frame(?)/bone is connected (as one piece), is it not?
And, about “physical wave” and “energy”: Assuming a “probability wave” is a physical wave, does it carry energy?
What are the (minimum?) “required” conditions/properties for “a wave” to propagate (or exist) in the universe? When I imagine “a wave” to propagate, it must at least be able to change/affect/influence its immediate neighbor’s condition (something that is right next to it), and this in turn changes another neighbor’s, and so on. My question is:for “a wave” to propagate, does its field (Z(x,t)) or medium have to be smooth and “continuous” (or can be discontinuous)? If so, why is it a required condition? (a field is not a medium but I must admit when I think about how a wave propagates I imagine something more like a medium with some kind of internal structure) It seems even if each local entity (a constituent of the medium?) is not connected to the next one, a wave can still propagates if a constituent can bump into (or interact only at a certain distance with?) the next constituent. If we assume its field (or medium) is continuous(or discontinuous), what kind of theoretical or observational inconsistency does it create or solve? (or maybe neither creates inconsistency?)
Another question:does any type of (propagating or non-propagating) wave always carry energy? or some waves could exist without energy (or with zero energy?)?
Mathematically, all a wave really requires is that there be something approximately continuous (absolutely continuous isn’t necessary — a lattice will do) and roughly uniform, arranged so that activity in one location induces a similar activity in nearby locations.
The best way to understand this is intuitive. Think about a “wave” at a football stadium; what is required for it to propagate around the stadium? A roughly uniform and approximately continuous distribution of spectators; the ability of each spectator to respond to the actions of the spectator next to him or her; and someone to get the whole thing started. And that’s about it.
Any physical wave carries energy. All changes of any sort, in nature, require energy.