During the 20th century, particle physicists learned that it is important to consider all the possible symmetries that the laws of nature governing elementary particles might exhibit. The presence or absence of symmetries can reveal aspects of nature that aren’t otherwise obvious.
Of the many possible symmetries to consider, there are three simple ones that play a unique role: charge conjugation (C), parity (P), and time-reversal (T). These three transformations, which affect particles, space, and time, involve
- C: changing all particles to particles of opposite charge (including electric charge, but also other less familiar charges; even some neutral particles get switched. For instance, neutrinos switch to anti-neutrinos, and neutrons switch to anti-neutrons.)
- P: putting the world in a mirror (more precisely, flipping the orientation of the three directions of space)
- T: running the world backwards in time (more precisely, flipping the direction in which time evolves.)
Each of these transformations has the feature that if you do it twice, you get back to where you started. In jargon, we say P² = P × P = 1 (i.e., if you put a mirror in a mirror, what you see looks the same as if there were no mirrors at all), and similarly C² = 1 and T² = 1.
Also, you can do two of these transformations together. For instance you can do C and then P, which we simply write “CP” (or you can do PC, which is the same — for these transformations, the order doesn’t matter) in which you put the world in a mirror and flip particles’ charge. You can also consider CT, PT, or even CPT. Like C, P and T themselves, any one of these combined transformations, performed twice, gives back the world you started with.
Now what should you do, now that you’re thinking about these transformations? The question which you should ask is this: if I imagine a world which is created from ours by making one of these transformations, do the laws of nature that govern elementary particles and forces work the same way in the transformed world as in our own?
If the answer is “yes”, then everything that can happen in the new, transformed world can also happen in our own; and in this case we say this transformation is a symmetry of our world. More precisely, it is a symmetry of our world’s laws of nature. If not, well, then you can still do the transformation, but it’s not a symmetry of our world, because the world you get after the transformation differs from our own.
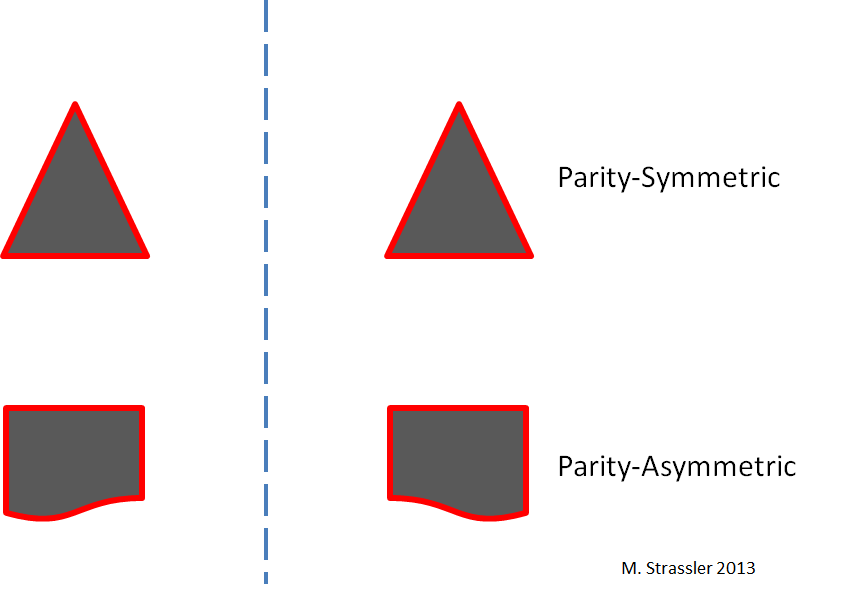
It’s not hard to get a feel for how parity (P) works. A particular object may or may not have symmetry under parity. As shown in Figure 1, reflecting a simple triangle in a mirror gives back a triangle which looks identical to the first one, so the triangle is symmetric under P. But the more complicated shape shown at the bottom of figure 1 does not look the same in a mirror, so it is not symmetric under P.
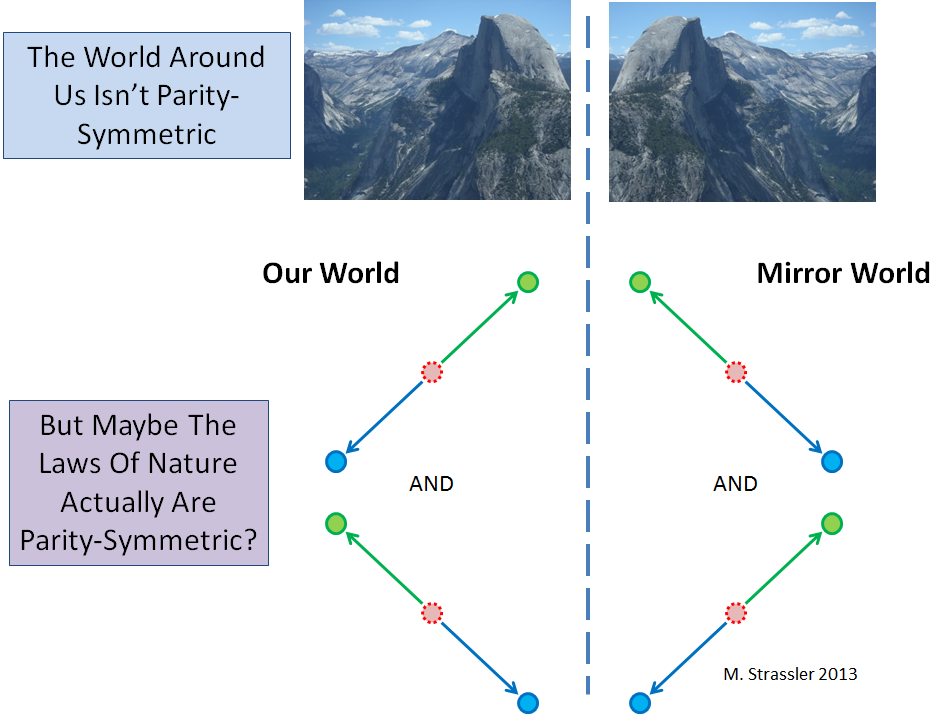
Obviously the world around us is not symmetric in a mirror, as you can see in any natural photograph (see Figure 2, top.) However, we have to distinguish between the symmetry of an object and the symmetry of the laws of nature that govern all possible objects. The underlying processes of particle physics could be symmetric, which would mean that for any process that can happen in nature, the mirror image of that process could also happen (Figure 2, bottom).
But in fact, the underlying processes of nature are not symmetric under P!
The remarkable thing is that neither C, nor P, nor T, nor CP, nor CT, nor PC, is a symmetry of nature. The basic processes that physicists knew about up through the early 1900s — in particular, those involving the gravitational and electromagnetic forces, and therefore those that hold the earth together and in orbit round the sun, and those that govern the physics of atoms and molecules and all of chemistry — are in fact C, P and T symmetric. So it was quite surprising to physicists when, in the 1950s and 1960s, it was learned that the weak nuclear force violates all of these symmetries. The only one of these transformations that is still widely believed to be a symmetry of nature (for profound theoretical reasons) is CPT.
Note that if CPT is a symmetry, then CP and T must have the same effect. Since it is a symmetry, doing CPT gives you back the world you started with, but we also know that doing T twice gives you back the world you started with, so CP must be do the same thing as T. The same is true for CT and P, and for PT and C.
CPT transforms particles and their interactions of our world to anti-particles and their interactions of the transformed world, and vice versa. And since in our world, every type of particle has an anti-particle [possibly itself again], and since every interaction involving various particles has an anti-interaction involving their anti-particles (so to speak), this is believed to be an exact symmetry. More specifically, in any world whose particles are governed by quantum field theory, the math used in the equations of the Standard Model, which describes all the known particles and forces, one can prove that CPT must be a symmetry. (Whether this is true of a fully unified theory [such as string theory] that combines a quantum theory of gravity with the non-gravitational forces isn’t clear; but experimentally no violations of CPT are known.)
C and P Aren’t Symmetries, Because of the Weak Nuclear Force
Up to around 1950, everything physicists knew — all of chemistry and atomic physics, all the effects of gravitational and electromagnetic forces, light waves and the basics of atomic nuclei — was consistent with the world being symmetric under P. But it turns out that C and P aren’t even close to being symmetries of the laws of nature. They are violated about as much as they possibly could be, by the weak nuclear force.
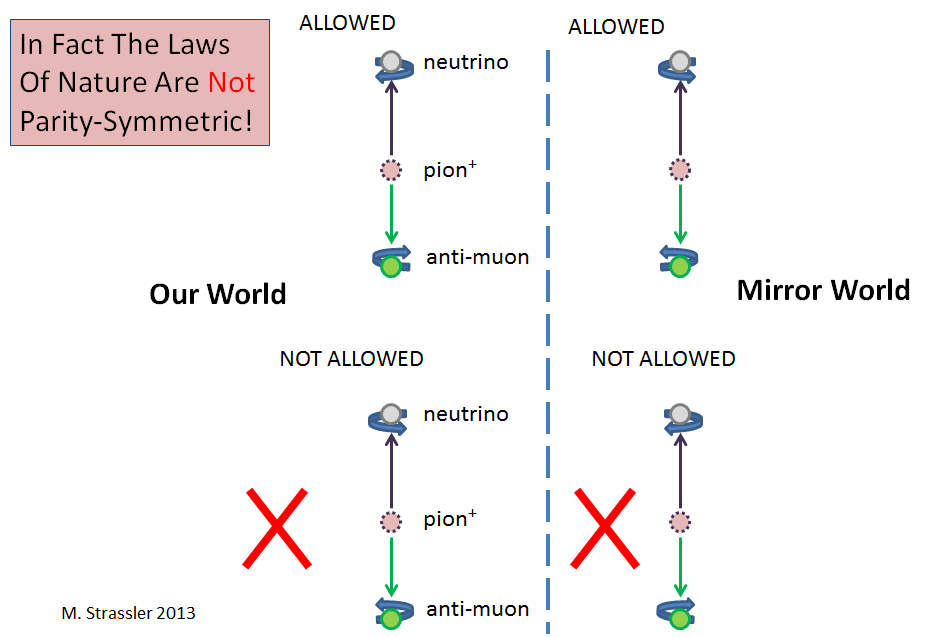
The simplest (but by no means only) example of this involves neutrinos. When a neutrino is created in a particle physics process, it is always produced via the weak nuclear force. And when it is produced, it always spins counter-clockwise, seen from the point of view of someone at its departure point. (Neutrinos, like electrons and protons and many other types of particles, are always, in some sense, spinning; more precisely they have angular momentum that is always present.) In other words, it spins like a left-handed screw (see Figure 3). [The jargon is that it has negative helicity — helicity as in “helix”, appropriate for a screw.] But a neutrino produced via the weak nuclear force never spins like a right-handed screw. Since P would exchange right-handed and left-handed (as you’d expect for a mirror), this means that the weak nuclear force violates P.
As a more specific example (Figure 3), when a positively-charged pion (a hadron made from an up quark, an anti-down quark, and many gluons and quark/anti-quark pairs) decays to an anti-muon and a neutrino, the neutrino is always left-handed and never right-handed. That violates P. And meanwhile, when a negatively-charged pion decays to a muon and an anti-neutrino, the anti-neutrino is always right-handed. This difference between the processes involving negatively and positively charged pions violates C.
This type of P and C violation is now very well-understood. The Standard Model (the equations we use to describe all the known particles and forces) incorporates it very naturally (see here for some discussion), and the details of its equations have been tested very thoroughly in experiments. So while the violation of P and C was a big surprise in the 1950s, today it is now a standard part of particle physics.
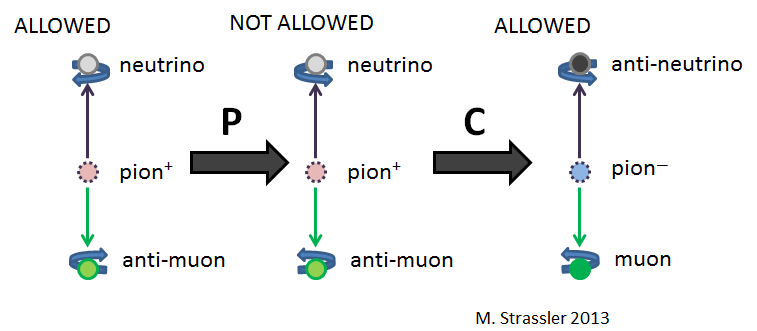
However, if we simply look at the particles themselves (and not in detail at how they interact with one another), CP (which is the same as PC) does at first appear to be a symmetry. That’s because P flips the spin of the neutrino from left-handed to right-handed, but C flips the charge of the pion particle, turns the anti-muon into a muon, and replaces the neutrino with an anti-neutrino; and the resulting process does occur in our world (see Figure 4). So for a brief period, physicists thought the weak nuclear force would preserve CP, even though it maximally violates C and P separately.
[Another way to see this is to look at my article on what the particles would be like if the Higgs field were zero. There you see that there are, for instance, electron-left and neutrino-left particles which come together in a pair, and are affected by the weak isospin force, while the electron-right particle comes separately from the neutrino-right particle, and neither is affected by the weak isospin force. Meanwhile what is true for the electron-left is true for the positron-right, and what is true for the positron-right is true for the electron-left. But P exchanges the electron-left and the electron-right, so clearly it is not a symmetry; C exchanges the electron-left and the positron-left, and since the positron-left is not affected by the weak-force, C is also not a symmetry. Note CP, however, exchanges the electron-left and the positron-right, both of which are affected by the weak nuclear force.]
CP Also is Not a Symmetry
But it turned out, as was learned in the 1960s, that CP is also violated in the weak nuclear interactions. Again this was a surprise, one that we understand well but are still studying today. Here’s the basic story.
Most hadrons [particles made from quarks, anti-quarks and gluons] decay almost instantaneously via the strong nuclear force, in times shorter than a trillionth of a trillionth of a second. One hadron, the proton, is stable; the neutron, on its own, lives about 15 minutes. (Atomic nuclei, made from protons and neutrons, are themselves sometimes called hadrons, but I personally prefer to call them “collections of hadrons.”) But a number of hadrons, historically and even practically of great importance, have short but not so short lifetimes — anywhere from a billionth of a trillionth of a second to a billionth of a second — and for most of them, their decay is induced by the weak nuclear force (while a few others decay via the electromagnetic force.) As I’ll describe elsewhere, some of them — especially mesons that contain one bottom quark or one bottom anti-quark — have one or more decays that have been measured to violate CP. (There are other signs of CP violation in oscillations between two hadrons, similar to oscillations that happen in neutrinos.)
This type of CP violation is very interesting because it occurs naturally if there are three or more “flavors” or “generations” of up-type quarks (up, charm and top) and three flavors of down-type quarks (down, strange and bottom). As Kobayashi and Maskawa pointed out, a version of the Standard Model with only two generations could not have this type of CP violation; there would need to be some entirely new source for it. Since they observed this back before any particles from the third generation were discovered, they essentially predicted there should be a third generation, and for this they were consequently awarded the 2008 Nobel Prize in Physics (along with Nambu, for his extensive work on other subjects.)
So far, there are no signs of CP violation from other sources than the one Kobayashi and Maskawa identified. But if there are particles and forces beyond those we know in the Standard Model, there may well be more places to see effects of CP violation.
However, even within the Standard Model, there’s still one very big puzzle…
The Strong Nuclear Force and CP
Very surprisingly, CP is not significantly violated by the strong nuclear force, and no one knows why. We know the strong nuclear force does not violate CP symmetry very much because of a certain property of the neutron, called an “electric dipole moment”.
The neutron is an electrically neutral hadron, very similar to a proton. The quarks, anti-quarks and gluons which make up the neutron are held together by the strong nuclear force. Now, an interesting question you can ask about any electrically neutral object is whether it has an electric dipole.
A magnet such as you played with as a child is a magnetic dipole, with a north pole and a south pole (see Figure 5.) A magnetic monopole would be either a north pole or a south pole, on its own; you’ve never seen one, and neither has anyone else. Meanwhile, an electric dipole has total electric charge zero but has a positively charge on one side and a negatively charge on the other. This could be as simple as a hydrogen atom, with an electron as a negative charge and a proton as a positive charge.
For a simple electric dipole consisting of two charges a distance D apart, one with charge q and one with charge -q, the electric dipole moment is simply defined to be q ×D. Notice that if the positive and negative charges sit right on top of each other, then this object has no dipole moment; the charges have to be separated in space to be “polarized”. A hydrogen atom normally isn’t polarized. But many molecules have a dipole moment, even though they are electrically neutral. For example, a water molecule H2O has a dipole moment equal to 3.9 × 10-8 e cm, where “e” is the charge of a proton (-e the charge of an electron), and “cm” is 1 centimeter. For comparison, this is just a little bit smaller than you’d get if you separated an electron and a proton by a distance that is about the size of a water molecule. (If you did that, the resulting dipole would have a dipole moment of about 9× 10-8 e cm). This is telling you that the electrons on the two hydrogen atoms in H2O are spending a lot of their time over with the oxygen atom.
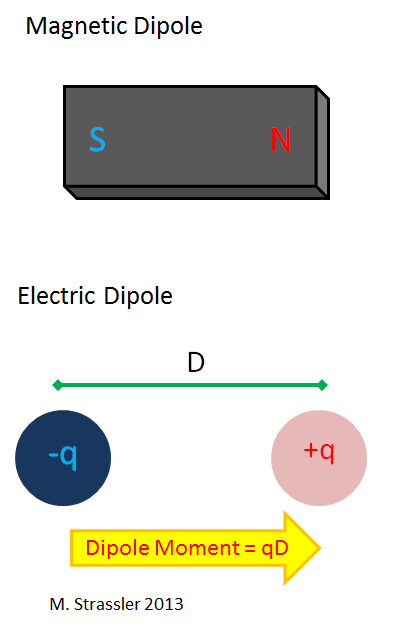
Now, how big would you expect the dipole moment of a neutron to be? Well, the neutron has a radius of about 10-13 cm, so you’d expect D should be about that size. And it consists of quarks, anti-quarks and gluons; the gluons are electrically neutral, but the quarks and anti-quarks have electric charges: 2/3 e (up quarks), -1/3 e (down quarks), -2/3 e (up anti-quarks) and +1/3 e (down anti-quarks). So you might expect q to be about that size. So you’d expect the neutron to have an electric dipole moment with a size in the vicinity of 10-13 e cm. That’s about a million times smaller than the dipole moment of a water molecule, mainly since the radius of a neutron is a million times smaller.
Actually there are some subtle effects which make a more accurate estimate a little smaller. The real expectation is about 10-15 e cm.
But if the neutron had an electric dipole moment, this would violate T, and therefore CP, if CPT is even an approximate symmetry. (It also violates P.) So if CP and CPT were exact symmetries, then the electric dipole of the neutron would have to be exactly zero.
Of course we already know that CP is not an exact symmetry; it’s violated by the weak nuclear force. But the weak force is so weak (at least as far as it affects neutrons, anyway) that it can only give the neutron an electric dipole moment of about 10-32 e cm. That’s far smaller than anyone can measure! So it might as well, for current purposes, be zero.
But if the strong nuclear force, which holds the neutron together, violates CP, then we’d expect to see an electric dipole moment of 10-15 e cm or so. Yet experiment shows that the neutron’s electric dipole moment is less than 3 × 10-26 e cm!! That’s over ten thousand million times smaller than expected. And so the strong nuclear force does not violate CP as much as naively anticipated.
Why is it so much smaller than expected? No one knows, though there have been various speculations. This puzzle is called the strong CP problem, and it is one of the three greatest problems plaguing the general realm of particle physics, the others being the hierarchy problem and the cosmological constant problem.
Specifically, the problem is this. When one writes down the theory of the strong nuclear force — the equations for gluons, quarks and anti-quarks called “QCD” — the equations have various parameters, including
- the coupling overall strength of the strong nuclear force
- the masses of the various quarks
- the theta angle, which does not affect any Feynman diagrams, but nevertheless determines the effects of certain subtle processes [quantum tunneling, with the buzzwords “instantons” or “pseudoparticles”] in the physics of gluons
Huh?! What’s that last one?? Well, this additional parameter of QCD was discovered in the 1970s (and is one of the contexts in which Polyakov, who won a pri$e recently, is famous.) The issue is too technical to explain here, but suffice it to say that if the theta angle isn’t equal to 0 or π, then the strong nuclear force violates CP. More precisely, and more disturbingly, it is a certain combination of the theta angle and the masses of the various quarks [specifically, the product of the complex phases of the masses] that violates CP. And these two things (the theta angle and the quark masses) are not obviously related to each other — so how can they combine to cancel perfectly? Yet for some reason this combination is zero, or at least ten billion times smaller than it could have been. There’s no obvious reason why.
Solutions to this 35-year-old puzzle include the following
- maybe the up quark is massless (this is a very difficult thing to check, because there’s no direct way to measure its mass; indirect methods have long suggested it has a mass a few times larger than that of the electron, but there are subtleties that make these methods difficult to interpret with complete confidence.)
- maybe there is a field called the axion field, which removes this effect; a prediction of this idea is the existence of an axion particle, which has been sought for over 30 years but hasn’t been found up to now. The axion could also serve as the universe’s dark matter, by the way.
There are a couple of other possible known solutions, but I won’t cover them here; generally they don’t have a near-term experimental consequence, unfortunately.
Addenda:
What does CP not being a symmetry have to do with the fact that there is more matter than anti-matter in the universe?
Do right-handed neutrinos and left-handed anti-neutrinos exist at all?
Coming soon…


33 Responses
Matt, I hope you don’t mind me continuing our main thread here because the squashed text won’t allow me to reply to your comment.
You said: “Handedness has to do with how things spin, which you haven’t referred to; but again, it comes with no arrow.”
After our long discussion and getting my thoughts together: I’m referring to the handedness of a coordinate system. Let’s say I have a clock and a right-handed coordinate system to label events in my frame. Someone else won’t observe the anticlockwise rotation of my clock relative to their clockwise clock in their frame, and they won’t observe a left-handedness of my coordinate system relative to their right-handed one.
Handedness of a coordinate system is fine — directly related to spin, too, since a top whose spin axis is the z direction may be made to spin from the x axis to the y axis and not the other way around — and it definitely flips under P. There’s real physics here: the weak nuclear force exhibits handedness, and the decays of muons whose spin axis points along the z axis are not symmetric under P. But why are you talking about “frames”, which don’t have any relation to P, and what does the observation of a rotating clock have to do with your point? I’m losing your thread. What are you trying to understand or to prove?
My thread was about me on the one hand being convinced that there’s an ‘arrow of handedness’ for space, just as there’s an ‘arrow of time’ for time, while you have shown in our discussion that this doesn’t make physical sense. In the end, what I really meant is that the handedness of one another’s coordinate system will maintain this handedness for all observers, just as the hands showing the time on one another’s clock will continue to turn clockwise as time runs ‘forward’.
I’m under the impression that the handedness of points in space can be actively transformed by P, or passively transformed by reversing the handedness of the coordinate system from right to left. Likewise their time coordinate can be actively flipped by T, or passively flipped by reversing the clock doing the time labelling so that its hands turn anticlockwise.
Okay, I think I essentially agree with all of that (except that focusing on a clock with hands probably adds additional confusing details, since the clock could well have been digital.) To speak more precisely, you would say not “the handedness of points in space” but “the handedness of the coordinate system” and/or “of spinning objects”; points don’t know about handedness.
Hi Matt, in the CPT transformed world, is the running of its clocks and the handedness of its measuring devices the opposite to those in our world?
Is C and ‘charge’ Q related to accounting for the structure and self interaction of a particle that flips under P and/or T?
I don’t know what that means, exactly. You can make measuring devices with either handedness, and they change places. And the definition of a running clock is ambiguous: the basic clock is something that vibrates or spins, and what determines whether it counts time forward or backward is how you use it: do you count the cycles forward or backward? A forward-running clock becomes a backward-running clock, but a backward-running clock becomes a forward-running clock — and so it is a question of what we humans chose to design, not of how the world actually works.
And I don’t know why you are asking about Q, structure and self-interaction here. C, P and T will change those things, but they’re not related to them.
As an example to highlight what I was thinking about that may interest other readers, take a charge +q moving at a constant velocity v from left to right on our computer screen and then reflected into the screen under R: (t, x, y, z) -> (t, x, -y, z). The magnetic field lines are now distributed around the charge in an anti-clockwise sense, opposite to what we observe in our world. But this is OK once I examine carefully the Lorentz force F = mdv/dt = qv x B: the LHS picks up a minus sign under R which I can cancel by adding a minus to the RHS that is physically consistent. One way is to add it to (v x B) and rewrite this as B x v , using a left-handed convention in this reflected world.
Likewise for time reversal under T where the RHS picks up a minus from the reversal of v requiring a -B to keep the LHS positive.
My comment was asking whether derived physical quantities in the transformed CPT world are defined in the same way as in our world, but using its transformed physical conventions which is an obvious yes, after thinking about it.
If we could accelerate neutrons and collide them as we do with protons, would the production of Higgs bosons be higher or lower?
For context, you probably want to read this post: https://profmattstrassler.com/articles-and-posts/the-higgs-particle/the-standard-model-higgs/production-of-the-standard-model-higgs-particle/ .
Protons and neutrons are related by an approximate symmetry of the universe in which you exchange all up quarks with down quarks and vice versa. This is called “strong isospin”, for what it is worth. It overlaps with but is not the same as the SU(2) of the Standard Model “weak isospin”.
The gluons in protons and neutrons are unchanged under this symmetry, and so the largest process for Higgs production, from collisions of two gluons ( g g –> H ) , is unchanged
The next common process is u u –> u u H , u d –> u d H, d d –> d d H, where “u” and “d” stand for up and down quarks in the colliding Higgs bosons. The combination of processes form a symmetric set under strong isospin, so they aren’t changed either.
The next is u dbar –> W+ H and d ubar –> W- H. The two processes would switch places, but again, the total rate would be the same.
Same for u ubar –> Z H and d dbar –> Z H.
Finally we have g g –> top anti-top H.
And so on. Viewed as a whole, the processes producing Higgs bosons are symmetric under strong isospin, and so exchanging protons for neutrons makes essentially no difference. The same would be true for exchanging protons for anti-protons.
However, if you switched *one* of the two beams, colliding protons with neutrons or protons with anti-protons, then this would not be true. While g g –> H would be the same, production of a W and a Higgs would change. For instance, in proton/anti-proton collisions (as were used at Fermilab’s Tevatron accelerator), u dbar –> W+ H is larger because there are more energetic down anti-quarks in an anti-proton than in a proton. But that statement becomes irrelevant at a super-LHC with high collision energies, because then you can make Higgs bosons so easily that you don’t need particularly energetic down anti-quarks, and at lower energy fractions the number of down quarks and down anti-quarks in a proton, neutron, anti-proton or anti-neutron is almost the same (as is the case for the number of gluons at lower energy fractions).
Matt, what has been your experience as a professional physicist on how your peers view the reversibility of handedness compared to the reversibility of time?
I find it amazing that left and right handedness is the space equivalent of time reversal forced upon us by SR, supposedly first discovered by Wigner in 1927. Two years earlier Thomas discovered the relativistic rotation of the rest frame of an accelerated point on its world-line as the space equivalent of time dilation.
Well, they’re both violated. In the context of relativistic quantum field theory, violating parity is easy as pie; it takes work to preserve it. It’s not that hard to violate time-reversal, either. So it’s generally viewed as normal that while CPT should be preserved, in a typical quantum field theory neither C nor P nor T will be a symmetry.
Historically, people came in with a bias that symmetries should be preserved in nature, but in retrospect, knowing what we know now about quantum field theory, it would have been a bit of a surprise if C or P or T were preserved. In fact, one of the great puzzles in the field is why the strong nuclear force seems to preserve CP even though there’s a very easy way for it to violate it. [The weak nuclear force violates P and C 100%, and has no problem violating CP (and, since CPT is preserved, violating T as well).]
Your last paragraph confuses me as I’m not really sure what you’re talking about. Time dilation isn’t related to time reversal, and I’m not sure which result of Thomas you’re referring to. But in any case, that’s not related to C,P and T.
I asked my first question because of the debate within the professional physics community on time reversibility within classical electrodynamics, CED, from 1900 to 1950 involving folk like Einstein, Feynman and Wheeler. The reversibility of handedness within CED on the other hand 🙂 was completely ignored by these guys at the time as far as I know, despite being equally important. Even today, there’s papers on ‘the arrow of time’ and time reversibility but nothing on the arrow of handedness and little on the reversibility of handedness, in comparison.
Matt, have you written a post on handedness and how this is related to there being more matter than antimatter in our universe?
There’s a fascinating exchange between you and Tim Preece in the comments in your post on Particle/anti-particle annihilation where you briefly mention this: https://profmattstrassler.com/articles-and-posts/particle-physics-basics/particleanti-particle-annihilation/#comment-8591. It seems a pity to me that this is buried in the comments.
Apologies for not making myself clear in my last sentence which isn’t related to C,P and T, but was meant as another example of how the history of SR has forced physicists to treat time and space on the same footing, even though they may believe they’re doing so at the time. In more detail for other interested readers:
Introductory SR books teach us that the points on a world line can be parameterized by the proper time of an imagined clock moving along it. But the rigidness of the imagined clock/point forces its proper frame to rotate relative to its co-moving inertial frame, when its acceleration is orthogonal to its velocity. So in the famous Twin Paradox: not only will the accelerated twin have aged less than the twin on Earth, but they will also have rotated in a way different to what’s intuitively expected.
The reason for the difference is that handedness isn’t an arrow, and that’s one of the reasons it isn’t discussed that way. Even though time and space are treated on the same footing post-Einstein, that doesn’t mean they are literally the same: time is one-dimensional and space is three-dimensional, and combining them into a four-dimensional structure doesn’t change that. Causality involves light cones — the two light cones of an event at the origin of a coordinate system lies at t = + Sqrt[x^2 + y^2 + z^2] and t = – Sqrt[x^2 + y^2 + z^2] — and that causal structure is not symmetric between time and space. So although time does have an arrow — there is a direction of +t and another of -t, and so T plays into the causality of the theory by switching future and past — space (x,y,z) does not have an arrow, only a handedness (i.e. is x cross-product y equal to +z or -z ?) and so P has no effect on causality, as you can see in the formula for the light cones I wrote, which is symmetric under switching z and -z.
Also, handedness (parity P) is not related to the matter/anti-matter asymmetry, which arises from charge conjugation times parity (CP), which in turn equals T in a quantum field theory or in any theory in which CPT is a symmetry. Parity is 100% broken by the Standard Model, and it breaks CP too; but similar theories that break P and *preserve* CP could not spontaneously generate a matter/anti-matter asymmetry.
(Modern experts often no longer use CPT. Instead they use CRT, where R is a reflection of one coordinate rather than all three; P is the same as R with an ordinary 180 degree rotation. This is just a technical detail though.)
Thanks Matt.
So from your comment, I should look at all four coordinates (x,y,z,t) rather than just (x,y,z) for an ‘arrow of handedness’: future-pointing with +t as one coordinate system, past pointing with -t of the opposite handedness to the first. The ‘arrow of time’ describes these two coordinate systems already so there’s no need for another label ‘arrow of handedness’; although it’s worth pointing out, at least to my mind.
You wrote: “P is the same as R with an ordinary 180 degree rotation”
I’m guessing that this changes when considering (x,y,z,t) space-time rather than ordinary Euclidean (x,y,z) space?
Actually I was trying to say something different. An arrow that can point front or back makes sense when pointing in one dimension. An arrow of time makes sense. But in three dimensions, what arrow would you choose? What is an arrow of space? How would you even define an arrow of handedness? Going to four dimensions makes it worse.
By definition, P (and R) specifically act only on (x,y,z). Time is left unchanged by this transformation; in short, P takes a point (t,x,y,z) to a point (t,-x,-y,-z). T acts on time, so PT flips (t,x,y,z) to (-t,-x,-y,-z) ; RT flips one spatial direction and time, for instance (t,x,y,z) to (-t,-x,+y,+z). An ordinary rotation around the X axis (let’s call it “X”) takes (t,x,y,z) to (t,x,-y,-z), and therefore P = RX and PT = RXT.
Matt, if I have a time-like vector (t,0), I can’t switch the sign of t for this event relative to the event at (0,0) by moving to another frame. The idea of there being an ‘arrow of time’ makes sense in this example. Likewise for a space-like vector (0,r): I I can’t switch the sign of r for this event by moving to another frame: I use ‘an arrow of handedness’ to express this idea; what in your opinion would be a better alternative(s)?
Is it correct to say that (t, r), (-t, r), (t,-r) and (-t,-r) are four coordinate systems with a different handedness and hence can’t be rotated into one another?
Ok, so this makes your issue clearer. The problem is the definition of “r”. What do you mean by “-r”? Normally by “r” we mean a radius vector. But a radius (unlike time) is always positive: r = sqrt[x^2+y^2+z^2]. There is no such thing as negative radius.
[NOTE ADDED: one way to see this is that under T, t –> -t, but under P, r –> r (as you can see from its definition above.)]
In a one dimensional space, we could use “x” instead of “r”, and “x” most definitely can be positive or negative. There is an arrow of space if space is one-dimensional. There is no such thing if space is three-dimensional.
A clearer way to say this is to look at what is happening infinitely far away. In time, there is past and there is future: the arrow of time can point to one or the other. In a one-dimensional space, at infinity there is left and there is right; the arrow of space can point to one or the other. But in a three-dimensional space, infinity consists of a two-dimensional sphere, and there is no special point on that sphere toward which an arrow of space should point, making it undefinable. “Toward the sphere” does not define an arrow.
Also, this does not have anything to do with “handedness”, which is a separate question, so I think you are mixing them up. Handedness has to do with how things spin, which you haven’t referred to; but again, it comes with no arrow.
If neutron has a dipole moment then T is violated? Why? Sorry for the dumb question. but why?
I believe That antimatter never existed in the universe,and the antiparticles are due the transformations of energy into mass and vice-versa,and are not conserved near the speed of light.the antiparticles are originated by the Pt symmetry breaking ,That are holes in the quântica vacuum
The violation of cp indi cate just than antimatter canto existe in the the antiparticles are energy locally bundleled in quantum vacuum, due the transformation not uniform in the spacetime and time, and than are restaure in the spacetime contínuos, w herética speed of light apear as constant tô all nature, and the neutrinos of right handed are reais, e the the antineutrinos are viver by reversão in the symmetry. It is pt is broken doping apear the antiparticles as pt reversão. PT the antiparticles are energies locally bundleled in quantum vacuum, because the transformation of mass and energy are not uniform tô relativististics speeds, apear inglês speed of light tô compensar the asymmetry of spacetime and time and restaure by the junction of spacetime and time into of spacetime
Contínuos. The né apear the broken rotational invariance.cpt in all is conserved
Is it possible that CPT gets violated when gravity is included in a quantum field theory (N fields means N!-1 violations?) If you only have two fundamental forces, could CP or CT get violated? Or is it only single letter symmetry that could get violated?
Or maybe with quantum gravity there is an extra symmetry?
I like how careful and precise you are with language, like when you say “And when it is produced, it always spins counter-clockwise, seen from the point of view of someone at its departure point.”.
I’m assuming you made sure to specify “from the point of view of someone at its departure point” since Neutrinos don’t go at the speed of light it is therefore possible to come up with a frame of reference where that same Neutrino spins clockwise.
Most popular science sources aren’t that careful.
An impressive share! I have just forwarded this onto a colleague
who was doing a little homework on this. And he actually ordered
me breakfast because I found it for him… lol.
So allow me to reword this…. Thanks for the meal!! But yeah, thanx for spending the time to discuss this topic here on your blog.
What is a gauge symmetry?
I have a disused PhD in astrophysics, but my specialty was computational MHD. My courses never had time for particle physics, general-audience material is mostly useless — when you’re asked to take absolutely everything on faith, it’s hard to believe any of it — and the only semi-technical introduction I ever found was Feynman’s QED. But obviously that’s 30 years out of date, and doesn’t have much to say about QCD or the Higgs field to begin with. I’m very glad to have found your site. It’s occupying an important void, I think.
Colin,
Maybe I’m not phrasing this correctly, but I will try:
A gauge symmetry is a transformation to a gauge field (i.e. EM field, weak, strong…) that leaves the physics unchanged. As a concrete example – in Electrodynamics, the electric and magnetic fields are determined by a scalar- and vector-potentials. However, they’re not UNIQUELY determined. We may add to the potentials the divergence of some scalar function without affecting the fields. Thus, there is a “choice of gauge” which can be made for convenience.
Honestly, not even my professors know where the term “gauge” originally came from… but I believe it usually refers to the vector fields in the SM.
the term “gauge” is coming from Herman Weyl’s attempt to unify gravity with electromagnetism in 1919
(https://en.wikipedia.org/wiki/Classical_unified_field_theories)
According to Relativity, there is a symmetry between space and time. Therefore, C and P violations cannot be distinguished from a T violation. So maybe we truly have a time reversal asymmetry instead of a CP violation, even if this violations are relatively well understood. CP seem to be violated because T is not supposed to be violated… :o)
A T violation will produce a C, a P or a CP violation. At least it is a possibility!
PS.: Your blog is one of the best in terms of clarity, reliability and interest among physics blogs.
PS2: (you can erased “one of”)
Thanks for this. Concepts around C, P, and T are somewhat more accessible fo me now. As an aside, I was struck by The diagram discussing magnetic and electric dipoles and the fact that magnetic monopole do not exist (maybe). Is there an analogy here with quark confinement given if you separate the N and S poles in a magnet by breaking it you just get two seperate dipoles. Do quarks behave similarly?