We’ve had lots of great new data on the searches for Higgs particles, especially from the Large Hadron Collider (LHC), in recent months. In this article I’m going to try to summarize the implications of those searches, to the extent possible. [Right now the article is still being built, so some subjects aren’t in yet, but there’s plenty in here for you to read. First version 9/2/11. Second version 9/4/11. Third version 9/8/11. Fourth version 9/10/11.]
You might want to read the Higgs FAQ first, or have it handy [the link opens in a new tab], if you’re not familiar with the Higgs particle, or just need some basic reminders. I won’t provide many of those reminders here.
The Higgs field (or fields) and its particle (or particles, if any) are collectively referred to as the “Higgs sector”. I’ll use that term as a catch-all in the following discussion. The simplest possible Higgs sector is the one that appears in the so-called “Standard Model of Particle Physics”, a set of equations describing all of the known elementary particles and the simplest possible Higgs sector: one Higgs field and its associated Higgs particle. [Actually that’s the way things are after the Higgs field becomes non-zero; to see what things are like before the Higgs field is non-zero, read this article, which shows the Higgs sector actually starts off with four Higgs particles, and ends up with one.] But far more complicated Higgs sectors, with many more fields and particles, might be present in nature. For them, the implications of the current Higgs searches are correspondingly much more complicated to characterize.
So I’ll start by explaining the implications of the Higgs search for the Standard Model Higgs, then gradually move toward more complicated cases. In order, you will find
- The Standard Model Higgs particle
- A Standard Model Higgs sector but with other new particles
- The case of two Higgs particles
- The case of five Higgs particles
- Supersymmetry: Five Higgs particles along with superpartners
- No Higgs particle (to speak of)
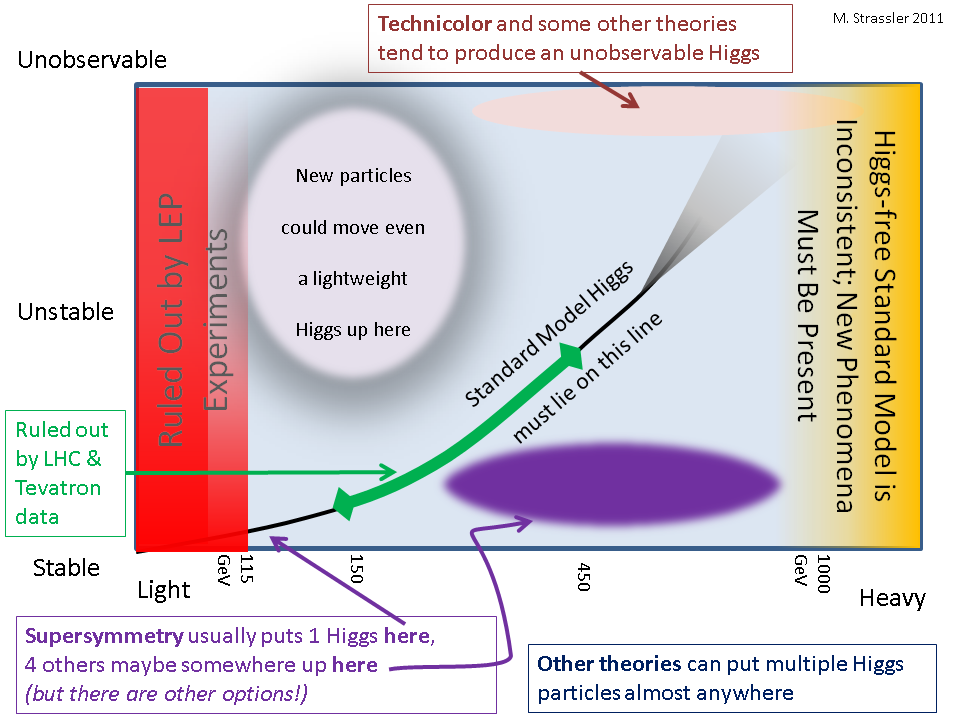
The article ends with a figure which summarizes some of the main observations.
The Standard Model Higgs particle
In using the words “Standard Model” I really imply two logically distinct assumptions:
- the Higgs field and particle are the simplest possible.
- there are no unknown types of particles in nature that interact with the Higgs field/particle.
If either one of these isn’t true, then what follows may be considerably modified.
Given all that we already know about nature, the only thing about the Standard Model Higgs particle that we do not know, if the Standard Model reflects nature, is its mass. If you knew the Higgs particle’s mass, the Standard Model equations would tell you the forces it exerts, how it is produced at the LHC and at what rate, and the probability that it decays in the various ways (or “modes”) that are available to it:
- to two W particles,
- to two Z particles,
- to two photons,
- to two gluons,
- to a bottom quark and a bottom anti-quark,
- to a tau lepton and tau anti-lepton,
- along with a few other more rare decay modes.
In short, it’s rather easy (relatively speaking!) to look for the Standard Model Higgs: for each possible mass, there are definite predictions of exactly what to look for. [Well, not exactly, because predictions are never infinitely precise, and some of the calculations of the Higgs properties — particularly, the rate at which it is produced at the LHC — are extremely tough, and even after thirty years of work are not more precise than 20 percent or so. But ok, remembering that no prediction is perfect, it is still meaningful to say that everything about the Higgs is predicted with reasonable precision if you assume it has a particular mass.]
So at the LHC experiments ATLAS and CMS, they pick one Higgs mass at a time and look to see if their data is consistent with the LHC producing, with the right rate, a Higgs particle of Standard Model type, decaying in its various modes with the right probabilities. I’ve explained the most important techniques they use (at least right now) in this article about the recent Higgs hints.
What do we know about the Standard Model Higgs right now, from a combination of theory and data? Let’s scan through the range of possible Higgs masses, expressing the mass as particle physicists usually do through its mass-energy (E = m c-squared) as a multiple of an amount of energy called a GeV, a bit more than the mass-energy of a proton (for more details see here.)
Above 450 GeV: This range has not been explored directly by the LHC, but there are strong reasons against it from other experiments. During the last 30 years, many measurements of a wide variety of quantities — asymmetries of certain types, similar to this one — decay rates for certain particles — etc., etc., have been made with very high precision, often to a percent or better. They’ve also been calculated to very high precision. And when such high-precision calculations are made, it turns out they indirectly depend on the masses of all the particles we know, especially the heavy ones: on the mass of the W particle, the Z particle, the top quark and, to a lesser extent, the Higgs particle itself. So, we have lots of high-quality measurements, and high-quality predictions, and we can ask: how well do they match?
Now the masses of the W, Z and top quark have all been determined experimentally, with high-precision for the top, very high-precision for the W, and exquisite precision for the Z. So the only thing in our high-quality predictions that isn’t known is the Higgs particle mass. It turns out that if the Higgs is heavy — conservatively, in the range above 400 GeV or so — the predictions don’t work very well at all. In other words, the predictions of the Standard Model equations for the existing high-precision measurements fail if the Higgs particle is in this range. It seems almost impossible that the Higgs could be as heavy as 450 GeV or above, if the Standard Model is correct; experiment and Standard Model theory just don’t match. The predictions work fine, however, if the Higgs particle is lighter — in fact, they work best if the Higgs particle is quite light indeed.
150 – 450 GeV: This range covers a lot of territory, and a few months ago I would have had to say many different things about it. But now I can just say this: with high confidence (and very high confidence in part of the region), the ATLAS and CMS experiments (and in some sub-range, even the Tevatron experiments CDF and DZero) should already have seen a sign of the Standard Model Higgs particle, if it were there. They see no sign, and therefore this region is experimentally ruled out, by the LHC (mainly) and the Tevatron. We can forget it — though I remind you, that’s for the Standard Model Higgs particle only!
130 – 150 GeV: Currently there are weak hints of a Higgs particle in this range, but some of this range, in particular the upper quarter, may be ruled out experimentally by the LHC’s August data. [Previous version said “upper half”, but with more careful analysis I no longer believe that.] The borderline will shift as more data comes in, and as the analysis of the data improves. By the end of the year this region should be definitively gone, unless, of course, the Higgs is sitting there.
115 – 130 GeV: This range, the most favored by indirect experiments combined with theory (see the discussion above about a Higgs heavier than 450 GeV), is the hardest experimentally, and the one in which the LHC will take longest to catch up to the Tevatron, which has an advantage for a technical reason I won’t get into right now. Currently there are no limits in this region, but the search will be at its height during the next six to eighteen months.
Below 115 GeV: Ruled out by the four experiments at the LEP II collider, the electron-positron accelerator which used to sit in the same tunnel as the LHC does now.
Now there are a couple of other comments worth making about the Standard Model, and the Higgs mass. These are a bit subtle. Let us ask this question: could nature consist of the Standard Model — its known particles and forces plus the simplest Higgs — plus gravity and its graviton particle, plus one new type of particle to make up dark matter, and nothing else?
The answer, if we assume for simplicity that dark matter is “inert” and does not in any way interact with the known particles except through gravity, is that this is possible only for the Higgs particle in the range of about 120 to about 160 GeV. Exactly where the upper edge lies doesn’t matter, since that region is already ruled out experimentally. The lower edge is more worthy of debate; is it 120, 125, 130? Maybe even a bit less than 120? But if the Standard Model Higgs particle were at 115 GeV, a plausible but not entirely definitive theoretical argument could be made that there would have to be additional particles in nature that we don’t yet know about. [The Higgs particle mass cannot simply be set like a needle on a dial, as it depends on many other things. What theorists do is use the fact that we know experimentally that the Higgs field is non-zero on average, with an average value of 246 GeV. Given this, we ask, can we find a way in principle that nature could give the Higgs particle any desired mass? It turns out that unless the Higgs mass lies above 120 or so GeV, subtle quantum mechanics effects make it impossible — without adding at least one more particle to the theory — for this value of the Higgs field to remain where it is. Instead, the non-zero value of the Higgs field would long ago have changed, suddenly and catastrophically, destroying the universe as we know it. This issue is called the vacuum stability problem.]
Unfortunately the consequences of this argument are exceedingly weak! These new particles, whatever they are, could be very heavy, perhaps millions, billions or even trillions of times heavier than the particles we can currently create at particle colliders. And we would know almost nothing about their other properties — how many are there, what forces do they interact with, etc. And on top of that, the theoretical argument about vacuum stability itself has some uncertainties. So if the Higgs particle’s mass-energy turns out to be at 117 GeV, and maybe even at 125 GeV, there will be debates about whether this does or doesn’t imply the existence of unknown massive particles. But the arguments won’t be conclusive, and they won’t probably lead very far… unless we get more information from some other experiment, or some new theoretical argument.
In summary: Experiment has narrowed the window for the Standard Model Higgs particle to 115 – 145 (140? 135?) GeV, the upper limit decreasing as the LHC accumulates data. Theory says that the purest form of the Standard Model (with only gravity and an inert type of dark matter) would give an unstable universe for a Higgs mass-energy that lies far below 130 GeV. However, a slightly impure form of the Standard Model, differing from the purest form only through the presence of new particles that are far too heavy to be directly produced, can accommodate any value in this range.
A Standard Model Higgs sector but with Other New Particles
All you have to do to change everything I’ve told you is add one new particle to the Standard Model.
For instance, if you add a new heavy particle that feels the strong nuclear force and interacts in some way with the Higgs, you will change the rate at which the Higgs particle is produced. Other types of new physics can have a similar effect. This can either increase or decrease the rate of Higgs production.
Or if you add a new lightweight invisible particle, so that the Higgs particle can decay to a pair of them, then some fraction of the time the Higgs particle, even when produced, can decay invisibly. In short, the rate at which you produce the Higgs at the LHC and it is visible in your detector goes down, making it harder to find. This could happen if the dark matter of the universe is made from particles to which the Higgs particle can decay, a scenario which is certainly not implausible.
The number of variations on these themes is very, very large. Thus, even a Standard Model Higgs sector can be much harder or much easier to detect in a world with other extra particles. And it is often very much harder to search for and exclude these variants.
One example of this type that is relatively easy to exclude is known as the “Standard Model with a Fourth Generation” — meaning that in each of the four classes of known matter particles (charged leptons, neutrinos, up-type quarks and down-type quarks) of which there are three flavors (for instance, the up, charm and top quarks are the three flavors of up-type quarks) we should add a fourth: a fourth charged lepton, a fourth [heavy!] neutrino, a fourth up-type quark and a fourth down-type quark. In such a world
- the rate for the main Higgs production process goes way up
- the rate for the Higgs to decay to two photons goes way down
relative to a Standard Model Higgs. Therefore the strategy for finding a lightweight Higgs (which in the Standard Model involves looking for its decays to two photons) switches to looking for decays to W and to Z pairs. Because the production rate increases so much, this possibility is rather easy to look for, and has already been almost completely excluded, for any Higgs mass, by the new LHC results.
But here’s another example: suppose the Higgs decays 90% of the time to unobservable particles, such as those of dark matter, and 10% of the time to the modes that we expect in the Standard Model. In this case, the rate at which the Higgs shows up in our searches is 1/10 of what we would expect, and so it will take at least 10 (and as much as 100) times as much data to find it or exclude it. And if the Higgs decays in an undetectable fashion 99% of the time, well, then we’re going to have to find it indirectly. And that’s possible, but takes a huge amount of data and some very clever techniques… it easily could take until 2018 or later!
And a third example: suppose nature offers up a new, rather lightweight hidden particle, one that does not feel any of the three forces of the Standard Model: the electromagnetic force or the strong or weak nuclear force. In this case the Higgs particle might decay most of the time to a pair of these new particles. And in this case, to find the Higgs particle, we would need to know how this new particle itself decays, because what we will observe in our detector are its decay products. But there are many options! And so, to find the Higgs in this case, or rule out this possibility, will require many different search strategies. Most of these searches haven’t even begun yet, and most of them won’t until we’re sure there isn’t a Standard Model Higgs.
The case of two Higgs particles
[For experts: I do not mean two Higgs “doublets”; that comes later. I refer here to an extra singlet.]
Just as one new particle outside the Higgs sector can change everything, so can one new particle inside the Higgs sector. That’s what we’ll consider here: the Standard Model, except with two Higgs particles instead of one. Let’s call the mass of the lighter Higgs particle `m’ and the mass of the heavier Higgs particle `M’.
Experimentally, what we find in such a theory (if M is less than twice m) is two particles that each behaves just like a Standard Model Higgs, except for one thing: the production rate for each of them is less than for a Standard Model Higgs. The lighter Higgs will be produced in the same way, and decay through the same modes with the same probabilities, as a Standard Model Higgs particle of mass m. The heavier Higgs will resemble a Standard Model Higgs of mass M. The only way we’ll know we’re not seeing double is this:
- Measure the rate at which the lighter Higgs is produced; divide it by the predicted rate at which a Standard Model Higgs of mass m would be produced; and call the result b.
- Measure the rate at which the heavier Higgs is produced; divide it by the predicted rate at which a Standard Model Higgs of mass M would be produced; and call the result B.
- Then, if there are two and only two Higgs particles, and everything else is the same as in the Standard Model, b + B = 1.
Now the only thing we know in advance about b and B is that they are both greater than zero and less than one, so both Higgs particles are harder to find than a Standard Model particle of mass m or of mass M. This scenario, therefore, is not as strongly constrained by current data as is the Standard Model; there could still be a heavy Higgs, or even two, with mass above 150 GeV, just with reduced production rates.
Remember that if you are looking for the Standard Model Higgs, you just have to specify its mass, and then everything is determined. In this model with two Higgs particles, we have two masses m and M, and also the parameter b (with B = b). There are now three things to specify before we try to look for these Higgs particles. It is much harder to search in three dimensions of possibilities than in one; compare trying to find your lost keys in an office building, where you have to look in many rooms on many floors, in all parts of the structure, to what you have to do when you know that you dropped your keys somewhere along a single long hallway. And so indeed, with just one extra Higgs particle, the search becomes significantly more challenging, and could take quite a while.
Moreover, if the two Higgs particles are different enough in mass — if M is bigger than twice m — there’s a wrinkle. Depending upon the details of the forces between the two Higgs particles, it may be that the heavier Higgs can decay to a pair of lighter Higgs particles! And if that happens, what I’ve said above about the heavier Higgs, and about how one checks this theory experimentally, may be completely altered. In this case some novel search strategies are required, and discovery could easily be delayed by several years.
The case of Five Higgs particles
A famous case that gets a lot of study is known as the two-Higgs-doublet model, and it has
- two Higgs particles h0, H0 that are electrically neutral and much like the Standard Model Higgs in some ways (similar to the case of two Higgs particles just described above). These are called scalar Higgs particles.
- one Higgs particle A0 that is electrically neutral but is very different from the Standard Model Higgs. This is called the pseudoscalar Higgs particle.
- one Higgs particle H– that carries the same electric charge as an electron, and one H+ that carries the same electric charge as the anti-electron — not surprisingly, referred to as charged Higgs particles.
You might wonder why five is a magic number. The reason goes back to what the Standard Model would look like if the Higgs field, instead of being non-zero on average as it is in our world, were zero instead. In that case there would be four Higgs particles, not one. And in the corresponding circumstance, this theory of five Higgs particles would have eight — 2 x 4 — instead. The counting is that each Standard-Model-Higgs-like set of fields starts off with four particles (and thus four, eight, twelve, etc, depending on how many such fields the model has) and from all of these three are used to make the W and Z particles massive.
There are now many different quantities to keep track of; masses for the five particles (actually four masses, since the H– and H+ charged Higgs particles are each other’s antiparticle and have the same mass), production rates, and a wide variety of decay modes. There is no simple way to describe all the different things that this model can do, and a wide variety of search strategies would be necessary to find it.
It’s impossible to give an exhaustive description of the many possibilities, so I’ll just make a few brief comments about how we look for these particles.
- Similar to (but not identical to) Standard Model Higgs particles, heavy scalar Higgs particles tend to decay to W and Z particles, whereas lighter ones tend to decay to heavy matter particles (such as bottom quark-antiquark pairs and tau lepton-antilepton pairs [top quarks are too heavy]), along with rare decays to photon pairs.
- Pseudoscalar Higgs particles, whether heavy or light, tend to decay like lightweight Standard Model Higgs particles: to heavy quarks and leptons, and rarely to photons.
- Charged Higgs particles also tend to decay to heavy quarks and leptons, but to conserve charge they have to decay to particles with different electric charge. For instance, the H– can decay to a tau lepton and a neutrino, or perhaps, if sufficiently heavy, it can decay to a top anti-quark and a bottom quark.
Unfortunately, while it is relatively easy to make scalar and pseudoscalar Higgs particles, making charged Higgs particles is not so easy, and so they are not so easy to discover. And it turns out that if the heavy scalar and the pseudoscalar are heavy enough, they too can often become quite difficult to observe. In fact, in that regime, where four of the five Higgs particles are heavy and one is much lighter, this model would look, at least at first, a lot like the Standard Model. A lightweight Higgs particle with Standard Model-like properties would be observed first, and only with very careful detailed measurements would it become clear that this Higgs particle is not quite standard. This is an example of why it will be so important to follow-up discovery of an apparently Standard-Model Higgs particle with high-precision studies of its properties; it might not be as simple as it first appears.
Although direct searches for these particles are still in early days, there are already many indirect constraints on this model — that is, if you keep all of the known particles, add the 5 Higgs particles, and nothing else, then one can make many predictions and show that many variants of this model are excluded already. But we will still be looking for these Higgs particles — especially since, if you add more particles — as in supersymmetry — then the constraints on the model actually become weaker, at least in some ways.
More sections still to be written:
Supersymmetry: Five Higgs particles along with superpartners.
Let’s turn now to supersymmetry, a theory in which every known particle must be supplemented by one or more “superpartner” particles, which have the same properties as their partners except that
- if the particle is a fermion, the superpartner is a boson (or vice versa).
- because supersymmetry is hidden, a particle and its superpartners have different masses (which would not be true if supersymmetry were manifest).
In this theory, at least in its minimal version with no additional particles beyond the ones that are absolutely required, the Higgs particles are five in number, taking the form described in the previous section. But there are two interesting differences.
First, the indirect constraints mentioned earlier that restrict the possibilities for the five Higgs bosons are weaker, because some effects that have not been observed [such as the increase in the rate for a bottom quark to decay to a strange quark while spitting off a photon] which could have been caused indirectly by, say, quarks are partially canceled by indirect effects from their superpartners, the squarks. In other words, particles and their superpartners give effects of the opposite sign (if the particles make a negative effect, the superpartners make a positive one, and vice versa). In general, cancellations between particles and their superpartners reduce the size of the indirect effects and thus lead to weaker constraints on the properties of the Higgs particles.
Second, there are new constraints of a different sort on the mass of the lightest of the scalar Higgs particles, the h0. In many theories, the strength of the force that Higgs particles exert on each other is unknown, and could be very strong or very weak. But supersymmetry relates the strength of this force to the forces involved in the weak nuclear and electromagnetic forces [more precisely the weak isospin and hypercharge forces]… and these forces are not particularly strong. Chug through the math and you find at first glance that, as a result, the lightest Higgs particle would have to be lighter than the Z particle, which has a mass-energy of 91 GeV — in which case experiment would already have excluded this theory. But a heavy top quark, which makes a large indirect effect on the Higgs particle mass. The top quark’s mass comes from the strength of the force that the Higgs field exerts on it, and interestingly the reverse is, in a sense, true — a substantial part of the mass of the h0 comes from an indirect effect involving the top quark. The stronger is the force between top quarks and Higgs particles, the larger is this effect. And it turns out (as we learned in 1995 from the Tevatron experiments) that the top quark is heavy, around 172 GeV in mass-energy.
Working out the numbers in the very early 1990’s, before the top quark’s mass was known for sure, a few of my colleagues were able to show that the mass of the h0 could be as large as perhaps 120 GeV if the top quark were that heavy. Since around the year 2000, the experimental lower limit on this particle’s mass is close to 115 GeV. So in this simplest, “minimal” version of supersymmetry, there is only a tiny window left for the h0.
That said, this small window lies within the remaining LHC search window for the Standard Model Higgs particle, about 115-145 GeV or so. In fact, as I mentioned earlier in discussing the Standard Model Higgs particle, the range below 130 is the most difficult region that takes the longest to explore. And furthermore, although the supersymmetric h0 is likely to resemble closely the Standard Model Higgs, this isn’t guaranteed; it might be harder to produce and/or decay less often in the fashion that is easiest to detect in that mass range (to two photons). So unfortunately, even if a Standard Model Higgs particle in the range 115-130 GeV is ruled out, that will not quite be enough to show that there is no supersymmetric Higgs particle sitting there. Somewhat more data will be required for that conclusion to be drawn.
In any case, supersymmetry may well not show up in nature as its simplest version, any more than the Standard Model itself is the simplest theory of its type. And in this case the lightest Higgs particle (or at least the one that most resembles the Standard Model Higgs particle) may well be somewhat heavier than 120 GeV. Still, we do not expect the lightest Higgs particle in a supersymmetric theory to be particularly heavy, and again, that is because the force that it exerts on itself is related by supersymmetry to the electromagnetic and weak nuclear forces, which are not particularly strong.
For this reason, if a Standard-Model-like Higgs particle is discovered where current hints suggest, around 140 GeV or so, it will imply (a) the minimal version of supersymmetry cannot be true, and (b) supersymmetry at the LHC will be viewed as considerably less likely by most particle physicists — though some loopholes will remain for a time.
No Higgs particle (to speak of)
As I have emphasized in the Higgs FAQ, despite the fact that there is an incredible amount of hype about the LHC being built “to find the Higgs particle”, the hype is misleading and even false to a degree. There is in fact no guarantee that there is a Higgs particle. All we know is that there is a Higgs field. But that’s ok! We’re not interested in the Higgs particle anyway, we’re interested in the Higgs field — and to understand that field is the real reason why the LHC was built. And the good news is that you cannot make the Higgs particle unobservable just with the particles and forces we know about. If you can’t find the Higgs particle, it will be because there are new particles and forces running about that should be visible (albeit perhaps with difficulty) in LHC data.
An example of a class of theories in which this occurs is called “technicolor”. [The name is just whimsy; it is given because it is analogous to the theory of the strong nuclear force, which also for whimsical historical reasons is called a theory of “color” (but this is just a word, not actually referring to what we see with our eyes as color.)] I won’t go through this theory in detail here (it needs its own page). For now, suffice it to say is that what happens in a technicolor theory is that there is a new, unknown, very strong force that is present in nature — let me call it the technicolor force — which pulls on new particles, let’s call them techniquarks, that feel the technicolor force but also the electromagnetic and the weak nuclear interaction [more precisely, the weak isosopin and hypercharge forces]. What the technicolor force does is compel the techniquark fields and anti-techniquark fields to bind together to form a new, composite field (see the Higgs FAQ for more insight into composite versus elementary.) This composite field is the Higgs field, in this theory, and the technicolor force compels it to be non-zero. (Recall it is crucial in nature that the Higgs field be non-zero; this is discussed in the Higgs FAQ and in a bit more technical detail on this page.)
[By the way, the technicolor theory is nice because the technicolor force does all of this at around the TeV scale, and this solves the hierarchy problem. Unfortunately the theory has other difficulties, which I won’t go into here.]
The resulting Higgs particle — the ripple of smallest possible intensity in the Higgs field — really never exists at all, and is not detectable. What do I mean by this? Here is a reasonably good analogy.
- Imagine you drop a big rock from high above into a pond. After a moment’s complexity following the splash, the water settles down, and all you see is a nice, outgoing ripple. That ripple can travel all the way across the pond. That’s what a nice, well-defined particle is like — a ripple that lasts a long time.
- Imagine instead you drop a rock in similar fashion into some hot molten tar. After a moment’s complexity, all you will see is a little disturbance near the point of entry, and then, nothing. There’s no ripple. A ripple in tar — or in honey, or in molasses — never really gets going. A liquid that cannot make nice ripples is analogous (and though the analogy isn’t perfect, the equations are really quite similar) to a field that has no associated particles.
You should also read what I had to say about why particles decay. That will give a similar, somewhat complementary viewpoint, with a related but slightly different analogy. The point is the same. If a ripple dies away fast enough — if it dissipates rapidly — you can’t even really identify it as such. And if a particle decays fast enough, it never really existed as a well-defined object.
So this is an example where there is definitely a non-zero Higgs field — a composite of techniquark and anti-techniquark fields — but no Higgs particle.
However, there is certainly something to discover! The technicolor force affects the process in which two W particles or Z particles scatter off each other, which can be measured at the LHC. The scattering rate becomes very different from that predicted by the Standard Model, and in fact, for sufficiently high energy, two colliding W particles can actually create a new particle, called a techni-rho, which would be quite spectacular in data. All of these phenomena are, with some difficulty, accessible to the LHC, once it creates proton-proton collisions with energies at or near to 14 TeV (you may recall it is running at 7 TeV collision energy until it shuts down in 2013 for a repair and improvement.)
I should say that the story behind technicolor is actually much more complicated than I’ve described here. (Of course that is true of supersymmetry too.) Many variants of technicolor are already excluded by data, though by no means all. The point of the presentation in this article was to emphasize that there are plenty of ways to have a Higgs field but no Higgs particle — but they always led to other new and observable phenomena that are not present in the Standard Model.
What are the implications of current Higgs searches for technicolor? If the Higgs particle turns up this year or next, that’s curtains for this brand of technicolor. If no Higgs particle turns up, then technicolor remains viable. In particular, if this scenario, or something like it, is the reality in nature, it is possible that we will not find the associated new phenomena until as late as 2020. Technicolor potentially pushes the LHC, in its current design and working at its maximum collision energy, to its limits. If we’re luckier than that, the new particles and forces that make the Higgs particle unobservable will show up much earlier — but this cannot be guaranteed.
Still to come: Some comments about some other theories…



34 Responses
of course llike your web site however you have to check the spelling on quit
a few off your posts. Manyy of them are rife with spelling problems and I in finding
it ver bothersome to inform the reality nevertheless I will defintely
come again again.
Question: If the higgs boson weight falls within the range predicting a transition from the current higher energy state to a lower state does that not also suggest that what we perceive as the big band could have been a similar transition from a higher energy state to the current one? What does quantum cosmology predict about a previous, higher energy state??
Implication of (heavy) dark matter masses
Dark matter particles are heavy almost by definition. If interact with Higgs field of the standard model, then they should be produced by collisions in either LHC or the the International Linear Collider on the drawing boards.
If they don’t, the implications should be even more interesting since some kind of field and interaction would be needed to make them massive. It would mean there are other fields and even forces in the dark sector.
Also, if we assume that the positron excess in the ATIC-2 (it could not distinguish electrons and positrons but show a sharp dip around ~850 GeV) and AMS-2 (high energy part is still collecting data), is true, and these are derived from dark matter decay, then it should be possible to find some Higgs life field/particle that connects the dark matter to the positrons and then they would have greater chance of showing up in the much cleaner debris of ILC.
What is your (@Strassler) opinion on the eXciting dark matter (XDM) theories that propose at least one new dark force.
Thank you for this nice site that I have just discovered.
I am not a particle physicist and some points are not clear to me:
You wrote here and somewhere else that the Higgs particle does not exist at all. And you give a nice analogy with the stone making ripples on water or honey. What I understand from these analogy is that we call particle something if it does not decay too fast. But where is the limit? For example the top has a lifetime of 10^-25 s (source wikipedia) while I have read somewhere that the Higgs could have something like 10^-22. Is the top a particle or not? What about the Ws and the Z?
Another question connected to the analogy with the electric field, that is, photons are kind of ripples of the electric field.
We don’t see photons in a static electric field, however there are virtual photons that can have attractive or repulsive behavior depending on the charge of the objects we study (is it correct?). Do the Higgs bosons play a similar role in the Higgs field? I mean are they virtual like the photons are in a electric field or like the Ws are in a beta decay?
Thank you for your help
The way I like to say it is that a particle’s mass defines its heartbeat — it ripples back and forth with a time that is T = h/m c-squared, where h is Planck’s constant. If the lifetime of a particle is less than one heartbeat, it basically doesn’t exist. The lifetime of a top quark is very roughly 100 heartbeats; a bit shorter for the W and Z particles. An example of a (composite) particle that barely exists is called the f0, formerly the sigma particle — its lifetime and heartbeat are comparable.
Given that more of the mass of the universe mass is in the form of dark matter than in the form of normal matter, it would not be surprising for there to be a number of dark matter particles equal to or greater than the number of standard model particles. For instance, if dark matter consisted of heavy (>proton mass) neutral, spin zero atom-like composite particles made up of an even number of light (~quark mass) fermions, each being part of a family with three generations and equivalent to normal matter fermions with the distinctions between leptons and quarks removed, what would this do to the Higgs particle possibilities?
Possibly nothing. Possibly everything. You would need to tell me (a) how the particles in the dark matter “sector” got their masses, (b) whether the Higgs field has any interaction with the new particles, and (c) whether the Higgs has any interaction with the fields that give those particles their masses. And a few more things. So your question isn’t specific enough.
If the Higgs field has no interaction with the particles in the dark sector, then obviously there’s no effect on the Higgs particle.
If however the Higgs particle is able to decay often to the particles in the dark matter sector, and all of those particles decay to other particles in the dark matter sector, then it is just as I described in section 2 of the article, and as shown in the figure at the end of the article [in the pink blotch at upper left]; the Higgs decays more rapidly, usually invisibly, and becomes harder to discover.
On the other hand, if the Higgs particle is able to decay often to the particles in the dark matter sector, and some of those particles can decay to known and detectable particles, then new classes of Higgs particle decays can be present, some of which could be spectacular and make the Higgs particle easier to find. Or they could be messy and make it harder. The number of options in this “hidden valley” scenario is too large to try to list here.
It is hard to be specific about dark matter. A logical possibility would be:
The Higgs field has an interaction with particles in the dark sector.
Dark matter fermions acquire mass in the same way as normal matter fermions.
The dark matter equivalent of electroweak bosons remain massless
Some of the dark matter equivalent of gluons acquire mass via a Higgs mechanism similar to that for electroweak bosons.
Thanks
Well I’m not an expert of course. I’m an engineer and I just follow the developments out of personal interest.
But I’m little confused with the symmetry issue. Yes the gauge symmetries are a redundancy of the description but they are also spacetime dependent global symmetries. Thus for each gauge symmetry there is a subset of symmetries for which the symmetry transformation is constant in each spacetime point. That’s why we have conserved charges realted to gauge symmetries etc. These subset of symmetries are real in the sense that they transform a state to a different state.
Your level of knowledge still exceeds that of a lot of particle physics graduate students — I would say that your response to my question (which is exactly the right follow-up) indicates that pretty clearly. I’ll tell you what — these kind of expert level discussions have their place, but what I’m going to do is set up a technical discussion page. I’d like to keep this site from scaring off the less knowledgeable… it’s purpose is not really to serve people who want as much technical info as you do. That isn’t to say that (as long as I have the time) I can’t provide that info, it’s just that I don’t want to fill the site with it. So let me set that up, and I’ll get back to your question.
Whoops?!
But discussing things just at the level of Prof. Susskinds “Continuing Stanford Studies” (http://www.newpackettech.com/Resources/Susskind/) or the “Demystified” book series (for example about supersymmetry: http://www.amazon.com/Supersymmetry-DeMYSTiFied-Patrick-Labelle/dp/0071636412) will be ok I think? These videos and books are intended to be watched and read by interested laypersons. While using these resources I would certainly be happy to ask something here sometimes if it fits in with a post from this blog 🙂
I`ll try it anyway 😛 …
Cheers
You should feel free to ask questions as you see fit. If I judge that we’re talking too much shop and should move the discussion to the technical zone, I’ll recommend that. I’ll try to find a good middle ground.
What is the difference between soft breaking and hard breaking of the EW symmetry? Also, can you talk about how topcolor, light higgs, and the rishon model fit into this higgs field.
Technical question, technical answer: See the answer to the previous question: there is no such thing as breaking of electro-weak (EW) symmetry, because there is no symmetry to start with. The Higgs field is often said cause “spontaneously breaking” (which is neither soft nor hard “explicit breaking”), but this is a gauge-dependent short-hand.
Regarding the other models — I may get to them eventually. Obviously if we see any sign of one of them in the data I’ll write a whole article about it.
Hello
So you are saying that we are absolutely sure that the EW breaks when a scalar field acquires a non zero VEV around the week scale; there is no other possibility. We call such field the ‘Higgs field’ and thus Higgs field exists by definition. Correct?
If I were answering a layperson or even a non-expert scientist, I would say this: there is no known way to have massive particles like the W and Z without a non-zero Higgs field of some type, though the available types are quite numerous. Moreover, a Higgs field also is necessary for the quarks and charged leptons to be massive particles. And finally, the decay of the top quark (which has been studied in some detail now) cross-checks this argument, because its decay to a bottom quark and a W particle tests whether the W and top have gotten their masses from a Higgs field. As you say, I call this field “the Higgs field” by definition, though of course there could be multiple fields playing some role.
For an expert, however, I would answer with much more caution, because in fact there are a number of subtleties here. First I would say: your question is not really well-phrased. The notion that electroweak symmetry is broken is an unphysical statement; electroweak symmetry, being a gauge symmetry, is not a real symmetry at all. [This is widely known among field and string theorists but seems never to have become widely known elsewhere… gauge symmetries are fake symmetries introduced to make calculations simpler. A real symmetry, like the rotational symmetry of a circle, is meaningful because it changes physical objects that are not symmetric, but all physical objects are symmetric under a gauge symmetry.] So clearly your statement that “electroweak (EW) symmetry breaks”, which is a shorthand widely used among physicists (I use it too) but is in fact inaccurate, can’t be exactly correct.
One correct statement is that the Standard Model is an excellent effective theory of W, Z, top and of course the other quarks and leptons, up to energy scales well above 200 GeV. That theory has a Higgs field, and it has two phases: a phase with a massless W,Z and top, and a phase with a massive W, Z and top. It is useful to describe the latter case as saying that there is a Higgs field that is non-zero, but the subtlety there is that this isn’t precise, because there is no gauge-invariant operator which makes this statement. The correct statement is that the W and Z longitudinal modes act (to good precision) as they should in a massive phase of a renormalizable theory with a Higgs field, and interact with top quarks exactly as they should. Period.
People have tried, of course, to get around this, but any modification of the Standard Model at the 100 GeV scale is now ruled out at the percent level by precision measurements. For instance, another way to get massive W-like and Z-like particles is to make them composite, built out of new particles in just the way that the ordinary rho particles are built from ordinary quarks. This excellent idea for the W and the Z is called the Abbott-Farhi model, but the model would suggest violations of Standard Model predictions that (I believe) would be at the 10% level or more — a range which is now excluded.
More generally, any attempt to make a version of the Standard Model that does not have a Higgs field would predict quantum mechanical corrections to Standard Model predictions that should be of order 10% or so. With dozens of measurements working at the percent level or better, this seems excluded by the data.
So my statement is partly a principled one and partly one that follows from data. Data forces us to a simple, renormalizable effective theory at the 100 GeV energy scale; such theories must have at least one Higgs field to reproduce the data. [But not necessarily a Higgs particle!!]
You stress in several places in your blog that the LHC is guaranteed to find the Higgs field regardless of the particular manifestation. But from the description of possibilities that you give above it seems that the Higgs could be nearly impossible to find (in a reasonable amount of time). Already, the technicolor scenario seems to strain the energy possibilities of the LHC. Perhaps, certain versions are even harder to detect such as a technicolor Higgs but also such that it interacts with a large or highly preferred hidden sector. Maybe something precludes such a scenario or maybe this difficulty doesn’t effect the detection mechanism for technicolor but… Bottom line is it seems quite possible to evade detection at the LHC. Or is my pessimism ill-founded? (Thanks.)
I think your remarks are not entirely ill-founded, but overall pessimism is certainly not warranted at this time. Don’t forget that the LHC experimentalists have many, many tools at their disposal; that they and their theory colleagues are very creative; and that we do not yet know the full capabilities of the LHC, which are likely to increase with additional hard work. Yes, there are scenarios which would be quite unpleasant and difficult. But in many of them we would discover other particles or processes along the way. So let us not, at this very early stage, become overly concerned. (By the way, I am preparing an article about this very issue, so keep an eye out for it in the coming week or two.)
thanks for your response. Just a quick follow up, “bottom line” question. Do I understand correctly that the currently quoted exclusion ranges for the Higgs mass apply only to the standard model higgs i.e. apply only to the case where there is higgs doublet and nothing else? The current exclusion ranges (must be above 114 GeV, cannot be 145–466 GeV except for some pockets around 250), all this does not apply if anything is different i.e. there are more higgses or some extra very massive particles, or if the Higgs is some effective field ? Anything besides the minimal Higgs scenario implies completely different (in most cases much weaker) bounds based on current data? Is this correct?
Essentially what you say is correct, I would just slightly water down your use of “completely” and “much”. If anything in the Higgs sector or what it interacts with is different from what is in the Standard Model, the bounds are different and often weaker. And it is common that the bounds are completely different and often much weaker. If we don’t find the Standard Model Higgs particle, the number of searches that the experimentalists have to carry out is huge. It could take all decade.
Higgs particles are fragile creatures, easily altered.
Supersymmetry with three “higgs particles”? Independently of the model, a massive gauge supermultiplet has one massive gauge boson, one four component spinor (or two 2-component ones), and one scalar. So for three massive gauge bosons, three scalars is the minimum, even if then there is not a mechanism to give mass to fermions.
Ah, I see. You are concerned because the particles are not organizing themselves the way you would expect if supersymmetry were exact. But you must remember that supersymmetry is hidden [“broken”] in nature, so particles do not organize themselves so nicely… for the same reason that electrons and selectrons do not have the same masses.
The right counting is the follows. If supersymmetry were exact, then of the 5 Higgs particles (h0, H0, A0, H+, H-), one neutral Higgs and the two charged Higgses would be superpartners of, and would have the same masses as, the Z0, W+ and W- particles, respectively. That would leave the other two neutral Higgs particles to be superpartners of the Higgsino particles.
But that couldn’t be the real world… so there’s no point in having LHC experimentalists search for it.
Does that answer your question?