Already I’ve had a few people ask me for clarification of a key point in the book, having to do with a certain type of unusual “standing wave.” It’s so central to the story that I’ve decided to address it right away.
The point that there are two quite different types of standing waves; the familiar ones you may know from musical instruments or from physics class, and less familiar ones that play a key role in the book. You can jump right to my new webpage comparing these two types of standing waves, or you can read the post below, which provides more context.
Note: Going forward, you’ll see a lot of posts and new webpages like this one. One of the great things about 21st century books is that they aren’t contained within their covers. I’ve always planned to continue the book into this website, allowing me to expand here upon key issues that I knew would will raise questions from readers. So even though the book in printed form is done and published, it will continue to live and grow on this website.
The Stationary Electron as a Standing Wave
In the book’s chapter 17, I suggest a sort of mental image of a stationary electron. In particular, electrons should be visualized as waves, not as little dots, and a stationary electron is a standing wave — a wave that vibrates in place. [I focus on a stationary electron because it’s the best context in which to understand an electron’s “rest mass” (see chapters 5 and 8.)]
If you know something about standing waves already, perhaps from music classes or from a first-year physics class, this statement is potentially confusing. An electron could be stationary out in the middle of nowhere, light-years from the nearest star. But the standing waves of music and physics classes are never found in the middle of nowhere; they are always found inside or upon objects of finite size, perhaps upon a guitar string, inside a room or in the Sun. So how could a free-floating, isolated electron out in the open be a standing wave?
This mismatch is naturally puzzling, and indeed it has already raised questions among listeners of my recent podcast appearances. [Here’s the conversation on Sean Carroll’s podcast, and here are the first half and second half of the conversation with Daniel Whiteson on his podcast.]
The point, which I didn’t have time to address in the podcasts and which is discussed in the book only in examples (see chapter 20.2), is that there is a type of standing wave that is not covered in first-year physics classes, and that appears in no human musical instruments that I’m aquainted with. Unlike familiar standing waves, it needs no walls.
Familiar Standing Waves
A string or other extended vibrating object may have many types of standing waves. For a string, the four simplest standing waves are shown below (Figure 25 from the book chapter 11; illustration by C. Cesarotti).
But we can just focus our attention on the simplest of all such waves, the one at upper left, which has a single crest that over time becomes a single trough and back again, over and over.
Classic examples of these simplest standing waves are found on the strings of guitars and pianos; somewhat similar waves are found in organ pipes and flutes. As budding musicians quickly learn, it’s generally the case that the longer the string or pipe or bell, the lower the frequency of the wave and the lower the musical note. An organ’s lowest notes come from its longest pipes, and shortening a guitar string with your finger causes the instrument to create a higher note.
[It’s not quite as simple as that because, as covered in chapter 10, there are other ways to change frequency; tightening a string raises it, while replacing air with another gas can raise or lower it. But for a fixed material with fixed properties, what I’ve said is true.]
A simple version of this basic idea is illustrated by taking a box whose sides are of length 
[In math, we would write
,
where 
Unfamiliar Standing Waves
However, there are other standing waves whose frequency of vibration does not decrease in this way. For standing waves of this unfamiliar sort, doubling the length of the box does not cause the frequency to drop in half. In fact, if the box is big enough, doubling its size barely has any effect on the frequency at all! (This can happen in unfamiliar materials, or in familiar materials treated in unusual ways; see chapter 20.2 for a couple of examples.)
If you put one of these unfamiliar standing waves in a box and make the box larger and larger, its frequency won’t drop all the way to zero. Instead it will settle down to a steady frequency, which I’ll label 
[In math, the wave’s frequency
The precise form of the expression depends on details of the box and the vibrating material; but the details are not important here.]
Summarizing the Two Waves
The size and shape of a large box thus affects these two types of standing waves differently,
- impacting the shape and the frequency of familiar standing waves, while
- impacting the shape of unfamiliar standing waves, but not their frequency
This difference is illustrated in animations found here, and in the graph below, which shows how the frequencies of familiar and unfamiliar standing waves depend on the length of the box.
A Wave that Stands Without Support
Suppose, then, that we take an unfamiliar standing wave and dismantle its box, or let its box grow to infinite size. Do we then have a standing wave that stretches all across the entire universe?! Well, mathematically speaking, this would indeed be true. But in realistic situations, the standing wave will always run into some obstructions around its edges. Perhaps your hand is close by, as is the ground and a nearby wall; trees and mountains block the wave in other directions, and so forth. Even out in deep space, the space is not completely empty; there are always stray particles moving by.
These objects will affect the shape of the standing wave. But if they are far enough away from the core of the standing wave, they do not affect its frequency — at least, not by an amount that anyone could readily notice or measure.
Thus even a realistic standing wave, with a diameter far smaller than the size of the universe, will vibrate at its resonance frequency if it is sufficiently isolated. That’s more than enough for the purposes of the universe.
The Importance of These Waves
And so an isolated, stationary electron corresponds to an unfamiliar standing wave whose shape is determined by its local environment, but whose frequency is not. It will vibrate at the same rate whether it is in deep space far from any stars, or whether it is in an empty, airless box the size of a sugar cube.
Why should we care? Because there is a direct connection between the frequency of this standing wave and the electron’s rest mass. Explaining that connection is the most important goal of the first two-thirds of the book (through chapter 18). In addition, there’s a link between this issue and the Higgs field — a topic of the book’s remainder (especially chapter 20.)
I hope I’ve managed to write this post in a way which is useful even if you aren’t reading the book. For those reading it, it may well be helpful in clarifying chapters 17-20, where these issues take center stage. If you have found this post confusing, please leave comments, or ask a question on my new Book Questions page. As always, your questions and suggestions will help me improve this website.
43 Responses
I agree with Michael Ehling here, this was clear enough even if I have not (yet) read the book.
On the Wave 0 (homogeneous solution) and Wave 1 (particular solution) solutions, I hadn’t appreciated how quantum physics explore all likelihoods – allowed by relativity – that classical physics do not. I am reminded how non-local entanglement behavior explore the correlations that lightcone causality is silent about. Roughly something like “Everything that isn’t forbidden will eventually (and even the unlikely “forbidden” things may) happen.”
Torbjörn, your premise is incorrect. Homogeneous and inhomogeneous solutions correspond to real particles and virtual particles, and have nothing to do with there being two types of standing waves.
The two types of standing waves are homogeneous solutions to two different wave equations. See https://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/waves-classical-equation-of-motion/
Matt, thanks! I admit to the confusion, since I remembered the non-resonant, extinguishing field disturbances of “virtual particles” which can have complex mass (but sum to zero mass eventually). In essence, they could be the particular solution of the initial problem.
The idea of wavicles being non-resonant when boxed in and slowly broadening when not is new to me, but I can see how that works out with the math.
[So it is “virtual particles” (and in their own ways, massive particles) that do exploration.]
Hi Matt Strassler,
Now that I’ve made a fully supportive comment, it’s time to get back to being me:
“Unlike familiar standing waves, [an electron standing wave] needs no walls.”
You are a very sharp fellow, so you have to know that’s not correct. The wave you showed is even _called_ “particle in a box” because… you know… boxes have walls!
More specifically, and simplifying terribly about those other two pairs of walls, particles get into these kinds of lowest-energy (single lobe) states _only_ when reflectively bound at each end. What you have shown is a variant of an electron p-orbital (not s, p) “cut and unwrapped,” so the ends reside at opposite ends of the box instead of interacting with each other.
So, someone reading this might now say: “But electrons exist in free space without walls!” Sure they do: As _wave packets,_ which are more akin to multi-frequency sharp laser pulses than simple sinusoidals. And even those wave packets spread and spread pretty quickly!
So fine, fine, fine. Terry, you silly fellow, take the box end off and… Voila! You have a simple sinusoidal wave representing an electron! No walls are needed! Point proved!
Except…
No, that’s not what you get, not even close. What you get is a _very fast spreading wave function_ that represents two superposed states: An electron moving to the left, whose wave component looks like a rapidly spreading cork-screw motion in the “rope,” or an electron moving to the right with a similar but opposite helicity cork-screw motion. Both have well-defined velocities (momenta) due to the sharpness of the original confined-to-a-box states, and both move _away_ from the box region faster than they spread in their length, thus quickly leaving the box region empty of any electron probability at all.
The electron escaped, but you don’t know in which direction. Conveniently, this is what you would expect at the classical limit of removing both walls with a box bouncing between them.
The wave function, however, has two regions of location probability with a potentially huge gap between them. There’s a word for that: Entanglement! You don’t need spin to get entanglement. You only need a true, universal unknown bit of information, and in this case, the unknown is a true, single bit, literally a qubit:
Did the electron go left (call that “0”) or right (“1”)? Both have equal probability!
If the box worked well enough to produce a resonant standing wave, then the two states were truly and genuinely quantum entangled. When you collapse this superposition, you get _either_ an electron moving left with a well-defined momentum or the same electron moving the right with equally well-defined momentum.
So again, do electrons travel in one direction in a fashion mostly like particles? Sure they do, though the “particle” part often gets grotesquely exaggerated in the minds of many beholders. Our brains work that way. What is going on is almost entirely waves until the wave function hits something and “clicks” into a captured electron. But more importantly, to get a particle-like electron moving in one direction only, you need a more complicated wave function than a simple, inherently two-way-ambiguous sinusoidal. It works best if you have fairly complicated wave packets, ideally ones that work a bit like solitons.
———-
And since I do this sort of thing intentionally and frequently and have even helped more than one small company become a big company by doing it (I love it when that happens), has anyone built a quantum computer using the kind of super-simple qubits I just described? I’ve never seen them in the literature, yet they are one of the purest, simplest, and truest forms of qubit I can imagine. It seems like there’s potential there.
I think “boxed in qubits,” biqs, makes a decent name for momentum pair qubits.
Thank you, Matt Strassler, for tempting me down this analysis path! Until you claimed “no walls,” I had always accepted, as you did, that the single sinusoidal is the best capture of a free electron. I never would have gone down this path without you tempting me!
You would do nothing more than confine particles in boxes and release the box ends simultaneously. You then get a qubit splitting off along two literal branches, which could interact with other similarly set-up qubits. The speed would not be tremendous, but I’m guessing these qubits would be much easier (and probably “warmer”) to create than most cryogenic approaches to quantum computing.
Momentum-pair, particle-in-a-box qubits would be much easier to design since they convert into mechanical ball computers at the classical limit.
Terry, you’re writing increasingly long posts here, and as they are full of misunderstandings, they aren’t helpful to you or to anyone else. I can’t respond to something this long, other to say that it’s full of errors from start to finish.
When you say “You are a very sharp fellow, so you have to know that’s not correct.”, you are only showing that you don’t yet understand the math or the physics that I’m trying to convey, and that you are overconfident in your knowledge. You need to read chapter 20.2 of the book.
I love it! The electron-in-a-box jump rope! If x is the length, I like projecting the complex phase plane onto yz, which makes the up-and-down wave into a lovely one-loop skip rope, with excited states matching the fancy tricks folks do by adding two or three peaks and troughs to the rope, versus just one. As Feynman noted, the speed at which the skip rope rotates becomes another way of saying “its rest mass.” If the rope starts moving left or right relative to the observer, the simple loop starts looking like a helix. The final bonus feature that I like best for quantum visualization is that if you scale the total volume enclosed by the rotating loop to 1, the fraction-of-1 volume enclosed by any one or two perpendicular-to-x slices becomes the probability of finding the electron in that region using sufficient high-frequency probe: Highest in the middle, dropping off to zero at the ends.
I was just reading the book today and wondering what the answer to this was! Thanks for the answer, it was very helpful.
One thing I am having trouble with in the book is the insistence that “wavicle” and “wavefunction” be treated entirely separately. Of course, trying to treat these as entirely separate entities would cause coherence problems mathematically. For instance, QFT is a generalization, not a replacement of, traditional quantum theory. Thus, all the elements of quantum theory, such as the wavefunction, must be deducible from QFT. If the wavicle could not reduce to something at least related to the wavefunction in the non-relativistic limit, this would create internal contradictions in the theory. In addition, I’m not exactly even sure what the “units” of a wavicle are. That is, what function describes a wavicle as a function of space, what PDE describes its evolution over time, and what are the units of the variables in that equation? (For the non-relativistic wavefunction, one has units of probability amplitude and the equation being the TDSE)
When reading through the book, I tried substituting in “single particle position-space wavefunction” for “wavicle” and it seems to work just fine for most cases. Even if you do have to account for relativistic effects, you can just use the appropriate position-space wavefunction. So for instance for electrons, the Dirac equation wavefunction would be the one to use, and for Higgs the Klein-Gordon equation wavefunction would be used.
There is a direct relation between the wave function for a single particle and the shape of a wavicle. This is precisely what has led to so much confusion, starting already with Schroedinger himself.
But wavicles are simply a quantum version of classical waves with which you are more familiar. They are waves in fields that exist in three-dimensional space. The function that describes the wavicle, and the differential equation that it satisfies, ARE the equations of the quantum field… the quantum generalizations of the same types of equations that are used in classical electromagnetism. See https://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/
A wave function is something that has absolutely no classical analogue. (Well, that’s not quite true; something similar arises in Hamilton-Jacobi theory; but you wouldn’t want to confuse it with ordinary classical waves there either.) It is a wave that exists on the space of all possibilities. In a field theory, a wave function is a function of an infinite number of variables. For instance, a classical field is a function F(x,y,z;t) of space and time. The wave function of a field tells you the probability amplitude that the field takes the value F(x,y,z), and so it is Psi[F(x,y,z),t] — a function not of space and time, but rather a function of a function of space.
And so wavicles DO NOT reduce to the wave function in the non-relativistic limit. Instead, the wave function tells you the probabilities that the wavicles will be doing this or that. Again, wave functions live in the space of possibilities, which is much larger than the physical three-dimensional space that you and I live in. One can make a beam of wavicles; but the wave function describes the beam. Any attempt to conflate them will leave you in permanent confusion, so I strongly urge you to give up this line of thinking. Trying to insist that wave functions and wavicles are related simply takes you down exactly the same erroneous road that Schroedinger had to walk back; he really thought he’d shown that quantum physics was nothing other than showing that particles are actually waves, until he realized that in multi-particle systems, something much more mysterious is going on… and that leads to quantum entanglement, EPR, Schroedinger’s cat, and all the other intricacies of quantum physics.
Dr. Strassler:
on the “wave packet” or “blob”….. its usually described as being fairly localized in that the highest probability of the “location” is where the amplitude is highest, with the tails trailing off towards zero asymptotically, similar to your Figure 22 on page 141? isn’t this more like a wave pulse than a periodic wave? if the blob does not interact with anything, would it just keep spreading out to infinity? and if it interacts with something, lets say exchanging momentum and /or energy, it collapses back to a more “localized” state?
Yes, the wave packet will spread out… VERY SLOWLY, compared to the frequency of the standing wave. For instance, if you put an electron in a empty box the size of a sugar cube, and then removed the box, the electron’s wave will spread out more slowly than human walking speed, and thus take many seconds to reach the size of an ordinary room — all while vibrating a million billion times per second. So from the electron’s point of view, this is an incredibly slow effect.
The numbers behind this claim will form the basis of a future post, since you’re far from the only one with this question.
Are the electrons in a cathode ray tube best thought of as being in a wave-packet state? Are solitons not macroscopic examples of wave-packets?
The precise states of particles in a beam depend significantly on how the beam was prepared. But one may often imagine them as in states where they are very nearly in a state of definite momentum in one direction and fairly well-localized in the other two directions. In an extreme case one could imagine them as simple traveling waves heading in the z direction with their shape in the x and y directions modulated by packet structure (as in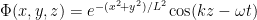
.)
The length scale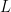
is not constant over time, and would gradually grow. That’s one reason (often not the most important) why efforts are always needed to keep the beam focused.
A soliton is specifically an objects that retains its structure indefinitely thanks to topology or to interactions. Wave packets are temporary and do not survive indefinitely, and they exist even in theories without topology or interactions. So naively, I’d say it’s best not to think of them as related, though maybe there are some situations where it’s useful to do so…
Prof. Strassler:
Thank you for the reply and stating a formula which greatly aids in a correct conceptualization. How close experimentally can a quantum be put in the state you presented. I presume it is a matter of scale so that the spatial extent of a proton at CERN with momentum known to several significant figures must have a spatial extent that “fits” within the equipment.
That is an issue in beam dynamics, and would be different for each collider. It also doesn’t really matter. What accelerator physicists are focused on is having a large number of particles traveling together, all with almost the same energy (and so the cosine part of the formula is important), but the shape of the overall beam is far more important than the wave packet of any one particle. The particles all affect one another, since they are all electrically charged, and they are also continuously being affected by the electric and magnetic fields of the accelerator. For these reasons, no one pays attention to the exact x and y dependence of the individual particles, as each one is different and of no consequence in the measurements. It’s just important to know that the quantity L is smaller than the dimension of the beam, and that’s assured by all the focusing magnets that make up part of the accelerator.
In almost any circumstance I can think of, it is enough to have a wave packet of the form F(x,y)cos(kz- omega t), where the function F is a localized blob of some type, not necessarily the one I wrote down. I am sure, however, that there are experts who, if they wanted to make a single particle on its own with exactly that packet shape, could get pretty close; but I can’t think of a reason why they would need or want to.
Clearly an electron is not a vibrating column of air in a tube, and (probably) not a vibrating string, but those are helpful analogies in understanding how it can be understood as a standing wave. Perhaps a better analogy, however, would be the wave of a pebble dropped in water. While the underlying physics controlling the resulting wave may be a little complicated, what we see is a localized standing wave with no boundaries, but with a comparatively small wavelength and greater amplitude at its central location. Like an electron, it is more likely to react to intersecting waves by splashing in the center, but it can at times interact at other, smaller crests as well.
No, there’s a reason I do not use a pebble dropped in water as an analogy. The relationship between shape and frequency is badly wrong. The standing wave for a stationary electron has only one crest, which alternates with having only one trough; the wavelength is infinite.
This is way clearer and crisper than I had hoped for, confirming to my mind that it’s OK to view the electron as having a real existence in some local region of space independent of an observer, and that probability and uncertainty kick in as the electron is increasingly confined to a region with a length roughly equal to the electron’s wavelength.
How correct was Louis de Broglie’s ideas on the wavelength of the electron compared to the picture you’re presenting?
I’m under the impression that he was seen as not quite correct at the time because the ‘wavelength’ was interpreted as that of a ‘wave function’ used to calculate probabilities; and not a physical wave length.
There is already probability and uncertainty if you ask whether a photon will scatter off this delocalized electron. You never escape these things in quantum physics. So don’t get too carried away with the idea of certainty and reality; quantum physics will come back and bite you.
De Broglie was focused on momentum and wavelength, not on energy and frequency. But he was right about that.
The confusion about wavicles (i.e. “particles” understood properly as waves) versus wave functions started right from Schroedinger himself, and has remained a source of confusion for 100 years. Quantum field theory got it straight, but not enough people learn it. You could also say that Einstein was seen as not quite correct for a time; Einstein originally suggested that quanta of light are “packets”, not “particles” — i.e., not dots. In a sense, he was right about that, but it took a while for people to get beyond Bohr’s views to see it clearly.
This is ongoing with respect to use of “wave packet.” Just trying to avoid undue indentation…
So, when using the “Pythagorean” energy equation you seem to be invoking your “Class 1” wave equations for which energy cannot vanish. Is this correct?
And, you ask us to think “field-theoretically.”
Presumably, the field is believed to be well-formed with respect to all of “empty space.” Is the isolation of a wave packet intended to correspond with region of the field having a uniform non-zero value with a boundary in the field having an average value of zero?
I think what you are saying is that there is a relation between E^2 = (pc)^2 + (mc^2)^2 and the Class 1 wave equation; exactly. The Class 1 wave equation, applied to a quantum, gives the energy-momentum relation with a non-zero “m”.
A cosmic field exists throughout empty space; I’m not sure what you mean by “well-formed”.
A wave packet is just the rough shape of a particle in a particle beam — which means it has roughly a definite momentum and a roughly constrained position, too, but not so definite in either that it violates the uncertainty principle. I don’t think I understand the rest of your question… but in any case, a field needn’t have an average value of zero for it to have a wave packet within it. The Higgs field with a Higgs boson in it could have the form “constant + wave packet”.
Thank you. I have to think about statement for the Higgs boson.
Dr.Strassler:
Was actually on a YouTube channel called Science Asylum by Nick lucid. Video: Quantum Fields Visualized.
A viewer asks, “is Wave Packet” a more correct term for the disturbance in the quantum field’?
The reply from Science Asylum: “No, wave packets are more of a quantum mechanics thing than a quantum field theory thing.”
I’m just trying to keep “terms” straight from a laymen’s perspective. Nick Lucid has some very good stuff on his channel.
I was glad to see you bring in the description of electrons in atoms in your answer to a question above, as I’ve wondered how my (probably dated) understanding of atomic structure fits in with the modern quantum field picture. I “grew up” with the molecular orbital description of chemistry, in which the electrons of an atom occupy probability regions (orbitals) with shapes of varying complexity depending on how many electrons they could accommodate: “s” orbitals were spherical and could only hold two spin-paired electrons, “p” orbitals were dumbbell-shaped and could hold three pairs of electrons, and so on through “d” and “f” orbitals. An awful lot of chemistry could be explained by visualizing how the orbitals of different atoms might overlap so as to allow their electrons to interact and form new chemical bonds.
In the quantum field picture, are the wave functions for the electrons in atoms the same as the ones used in the older orbital picture, or has the understanding of how electrons are arranged in atoms been changed substantially these days?
Not much has changed; most of atomic physics of the upper part of the periodic table is well described using the methods you described. The orbital shapes haven’t changed. In this context, quantum field theory just urges you to remember that the energy of the electron has an extra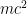
in it, which affects the orbitals’ frequencies — but in atomic structure and in most atomic processes, that shift in frequency is just a constant hum that doesn’t affect anything, so you can safely pretend it isn’t there.
That said, I am not an expert in the more subtle aspects of atomic physics. As you get to atoms with many more electrons, where on the one hand the outer orbitals can mix and on the other the inner orbitals are pushing their electrons close to the speed of light, there are probably a lot of interesting subtleties. Maybe one of my readers is more expert than I am about this. Even in this case, though, I would naively suspect that one can rely on relativistic versions of quantum mechanics, and that the full machinery of quantum field theory is not required.
Once you go beyond atomic structure to atomic and nuclear processes, however, then at some point you have to start using quantum field theory. Again, I’m not the expert on that, so I can’t give you specifics off the top of my head.
Sorry to post unrelatedly here, but: Will your book be published in the UK? Where can it be preordered if so, and is there a similar discount as to the American site you linked to a while ago? Thank you
Checking with the publisher. [For future reference: for a question like this, you can use the Contact Me page under “About” in the menu.]
Amazon are selling it at £23, from March 21st. (Link)
Thanks!
When I describe the wavelike nature of the electron to my high school physics class, I liken it to a standing wave traveling around the edge of a “singing bowl”, where there is no need for fixed edges because it is traveling in an area of space that is curved by the electric field such that it has a circular path. Is there any truth to this analogy/math that would back it up or am I horribly damaging my students?
Hmm… it’s not terrible, but it’s not really right either.
1) It’s more that the electron *fills* the bowl rather than traveling on its edge; in the ground state, the electron’s density looks like https://chemistrytalk.org/wp-content/uploads/2023/08/Screen-Shot-2023-08-12-at-1.43.07-AM-2-300×281.png and it vibrates in place, without changing its density over time. It has, in fact, no path at all.
Bohr’s original picture of hydrogen is not actually correct, even in 1920s quantum theory. While he guessed that electrons are on special orbits, the fact is that he got the right answer for the wrong reason; it was a lucky break. The correct picture (necessary to do anything more complicated than hydrogen) is that electrons do not orbit per se, especially the electrons in the lowest energy states, but instead form standing waves of various shapes inside the energy-well created by the electric field. In hydrogen, the various standing waves happen to closely correspond, by luck, to Bohr’s imagined orbits. So a somewhat better analogy than a traveling wave on the edge of a bowl would be to look at the standing waves of water in a bowl — which you could even demonstrate.
2) Perhaps this is just my misunderstanding your writing, but you don’t really want to say that “space… is curved by the electric field.” You probably meant “the curvature of the bowl is analogous to the deep energy-well created by the electric field.” The idea of space itself being curved triggers potential connections with gravity and Einstein, which would create confusions.
3) The standing waves in atoms and the standing waves I’m referring to in this post are somewhat but not precisely related, and indeed this is something I need to flesh out on this website. The issue is that quantum field theory and relativity add something that 1920s quantum physics (and its surviving form in most undergrad chem and physics textbooks) don’t have. In the usual story told to undergrads, the electron’s vibrational frequency is 1/2 m v^2, expressed in quantum language. That would decrease to zero if the electron were outside an atom, floating in empty space. In quantum field theory, we add in the mc^2 energy, which means that the electron vibrates much, much faster than undergrad quantum implies, and this vibration remains, even when the electron is in empty space.
[A lot of this is explained in chapter 17 of the book. But I will indeed need to say more about how atoms work within supplementary material on this website.]
mmm, feels ‘unfamiliar, because a standing wave ‘stands’ because of addition of a left-traveling and a right-traveling wave. both of same handedness. But my good old ‘familiar’ waves are produced by sources (and mirrors), not by vacuum. Looks like nature deep down is all ‘unfamiliar’ to us non-physicists. (ps. the book will come out here next month, ordered it, waiting…)
All standing waves are made somehow — there has to be a source. So that’s no different.
The surprise is that there doesn’t have to be a mirror… and that, indeed, is the key difference.
Suppose you make an electron and a positron from scratch, and do it in such a way that the positron moves away while the electron is left stationary in front of you. Congratulations, you have created a standing wave. And no, you do not need to think about it as a sum of waves moving in opposite directions; the equations for this wave are different from the ones you are used to.
Yes, Dr. Matt, that was clear even through I have not (yet) read the book.
Great! thanks for the feedback.
Dr Strassler:
Regarding the standing wave, standing on its own, in an infinite universe. I had always thought that the wave was able to stand on its own, mathematically, because the addition of many, many waves, similar to a Fourier analysis, allows one to construct a waveform that basically cancels everywhere (destructive interference) except for where the electron has the highest probability of being, where the wave forms exhibit constructive interference. in a certain sense, almost giving localization of the electron. Is that an improper understanding?
So, the answer is yes, and yet not quite, because you are missing something that is almost never taught in university quantum physics classes, and is only covered in graduate school. This deserves a long answer, and I will write one soon and put it into the FAQ for the book’s Chapter 17.
For today, here’s a short answer, suitable only for math/science nerds (apologies to everyone else.)
You are referring to what is generally called a “wave-packet”, and we may as well just call “a blob.” You can make an electron into a shape of a blob. (It will quickly expand into a larger and larger blob, unless something constrains it. But as we’ll see, this doesn’t matter.)
So let’s analyze this the way any quantum physics course would do in a university. Let’s call the width of the blob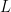
. By Fourier analysis, the range of wavelengths that contribute to this blob range between 
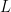and infinity. That in turn means, in quantum physics, that the speed that the electron can have ranges between 0 and 
, where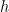 
is Planck’s constant.
In quantum mechanics class, we would then conclude [dropping all factors of 2 and
below to keep things uncluttered] that the electron’s energy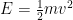 
can lie between 0 and 
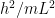. By the Planck-Einstein formula ![E=f[h]](https://s0.wp.com/latex.php?latex=E%3Df%5Bh%5D&bg=ffffff&fg=000&s=0&c=20201002)
, which applies for any quantum including an electron, we conclude that the frequency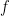 
lies between 0 and a maximum of 
.
As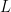
goes to infinity, this maximum frequency goes to zero, similar to (though slightly different from) the familiar standing waves I started with. And so, for large blobs, the electron’s frequency is tiny. So says quantum physics class.
But this leaves out something huge: Einstein’s relativity!!
We have forgotten, in our first quantum class, that the electron’s energy is not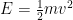
. Instead, it is approximately 
.
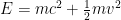When we account for this, and are slightly more careful with our relativity formulas, which state that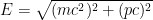
, where 
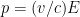is the electron’s momentum, we find that the frequency now lies roughly between a minimum frequency 
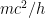and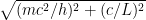 
.
This last expression, not accidentally, is of the same form as what is shown in the last equation in the post above! When the blob is large, the electron’s frequency lies in a very narrow range, not around zero but instead at and just above the electron field’s resonant frequency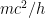
. Thus it is a standing wave whose frequency is large, not tiny; and if the blob is very wide, the average frequency remains high and the range of frequencies becomes extremely small.
And so, you see, by asking your question and including special relativity as we should of course, we obtain results consistent with this post. It all fits together!
Dr Strassler:
thank you for your detailed response, I had to read it a few times, but I believe I got the crux of it. Would “Wave packet” be a proper “term” to use in QFT?
I’ll give a less compact and more detailed explanation on the website sometime later this year. For people who’ve never really encountered quantum physics before, it’s not an issue that needs covering, so I didn’t mention it in the book. But for those who have, it’s crucial to highlight the difference between 1920s Born-Heisenberg-Schrodinger quantum mechanics and the later formulations of quantum mechanics and quantum physics; if you leave out the electron’s mass-energy, you truly fail to understand what an electron is.
Yes, “wave packet” is used widely.
Dr Strassler:
Thank you. The only reason I asked about ‘Wave Packet” being a proper term is because on another website, someone made an issue of “Wave Packet” belonging to Quantum Mechanics, not Quantum Field Theory. Again, sometimes confusing for us laymen.
Whose website says that? Maybe there’s some issue I’m unaware of.
But in none other than Steven Weinberg’s first volume (of three) on quantum field theory, when he is still defining what he means by quantum field theory, he defines scattering amplitudes; and to do it, he uses wave packets. It’s right there in his table of contents: in section 3.1 on “‘In’ and ‘Out’ States”, the first subsection is “Multiparticle states”, and the second is “Wave Packets”. They are rarely used except when setting up the basic mathematics, because you can usually get away without them. However, I’ve never heard someone complain that they should never ube sed in Quantum Field Theory. [One does have to be careful about what they mean in an theory with interactions, however.]
Dr.Strassler:
Was actually on a YouTube channel called Science Asylum by Nick lucid. Video: Quantum Fields Visualized.
A viewer asks, “is Wave Packet” a more correct term for the disturbance in the quantum field’?
The reply from Science Asylum: “No, wave packets are more of a quantum mechanics thing than a quantum field theory thing.”
I’m just trying to keep “terms” straight from a laymen’s perspective. Nick Lucid has some very good stuff on his channel.
Well, he’s wrong on this one.
Regarding wavepackets, they are (right or wrong) often used to model cosmological redshifts as the photons are traveling through expanding space.
I had tacitly assumed that they model the quantum field behavior in a cosmological setting well enough in a simple manner, and it seems from the discussion here I may go on using them.