It is quite amusing to find that just as I am drafting an article on mass and energy, in which Emmy Noether, one of the important mathematicians and mathematical physicists of the last century, makes a central appearance, the New York Times decides this is the day to make her deservedly famous among the wider public. A contemporary of Einstein’s, whose respect for her intellect is well-documented, Noether is certainly revered among physicists, but is surprisingly unknown outside of physics and mathematics.
If it’s any indication of her influence on my field, a search of a repository of papers in particle physics, quantum field theory and string theory over the last four decades finds her name in the title of 279 articles, which is pretty darn good for a mathematician who died over 75 years ago; for comparison, Einstein and Feynman’s names appear in over 5000 and over 1500 paper titles respectively, though they were full-time physicists and many things in modern physics were named after them. What Noether did in mathematics I can’t properly characterize — an expert in modern algebra will have to describe that — but within physics, Noether’s name is most commonly associated with a profound mathematical theorem of great importance for physics. It is the theorem that clarifies why some quantities in nature (such as energy and angular momentum) are conserved (physics language for “preserved”, or “unchanging over time”.) We’ll be celebrating the centenary of this theorem in 2015 (it was written down in 1915, though only published in 1918).
I’ll be putting up my mass and energy article up in stages; some part of it should go up tomorrow. In the meantime, enjoy the well-written and apparently correct New York Times article, whose only flaw, perhaps, is that it slightly over-states Noether’s role in physics (she wasn’t as important as Einstein, but that’s hardly a criticism) while almost completely neglecting her important achievements in pure mathematics, some of which also had a later role in physics. And also enjoy Einstein’s memorial tribute to her, which is likely the first time that her name appeared in the Times, and which gives perhaps a more properly balanced description of her achievements.



15 Responses
What i do not realize is actually how you
are now not really much more well-liked than you might be right now.
You are so intelligent. You already know therefore considerably on the subject
of this subject, made me in my view believe it from so many various angles.
Its like women and men are not fascinated unless it’s something to do with Girl gaga!
Your personal stuffs nice. All the time maintain it up!
Integrable or non-integrable – it does not matter. When we write the system energy, for example, we write a symbolic formula without knowing the numerical values of solutions involved into it. The funny thing is that in the Classical Electrodynamics with its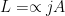 , we formally write down some conserved quantities, but solutions involved in them are non-physical. To get a physical solution we discard the self-action contribution and arrive at the third derivative
, we formally write down some conserved quantities, but solutions involved in them are non-physical. To get a physical solution we discard the self-action contribution and arrive at the third derivative 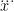 that leads to runaway solutions. Only using approximate
that leads to runaway solutions. Only using approximate  helps construct something that looks as a radiative reaction force, but the energy is not conserved in such a case. I wonder what the use of the Noether theorem (apart from self-fooling) is in this particular case.
helps construct something that looks as a radiative reaction force, but the energy is not conserved in such a case. I wonder what the use of the Noether theorem (apart from self-fooling) is in this particular case.
Integrable or non-integrable – it does not matter. When we write the system energy, for example, we write a symbolic formula without knowing the numerical values of solutions involved into it. The funny thing is that in the Classical Electrodynamics with its $L = – jA$, we formally write down some conserved quantities, but solutions involved in them are non-physical. To get a physical solution we discard the self-action contribution and arrive at the third derivative $\dddot x$ that leads to runaway solutions. Only using approximate $\dddot x^{(0)}$ helps construct something that looks as a radiative reaction force, but the energy is not conserved in such a case. I wonder what the use of the Noether theorem (apart from self-fooling) is in this particular case.
Integrals of motion exist without any symmetry; it is just an existence of solutions. Integrals of motion follow from the equation system, no Lagrangian is necessary. Symmetries may simplify the form of integrals of motion, but they do not fix the form: any combination of integrals of motion is also an integral of motion, so the form is not fixed. I am afraid the meaning of the Noether theorem is highly exaggerated in this respect.
That is an interesting point of view. I’m not sure how I feel about it. I do not know practically how I would use that point of view in the context of quantum field theory and quantum string theory, where generally the system is not integrable, and you have to go beyond equations of motion to calculate anything.
One thing that is for sure is a historical fact: that techniques based on Noether’s theorem proved very useful in the development of certain subfields of high-energy physics.
Matt, It’s well to remember that Emmy Noether was responsible for two very important and related theorems, not just one. The first more familiar one shows that the existence of a global symmetry implies a conservation law, but holds only provided that the equations of motion are satisfied. The second theorem relates to a local symmetry, and yields an identity (a “Bianchi identity”) among the equations of motion themselves. One place in which both theorems are discussed is http://nd.edu/~kbrading/Research/WhichSymmetryStudiesJuly01.pdf.
thanks…
Is invoking Noether’s theorem the only proper fundamental way to answer the question “what is energy”?
i.e. energy is the thing that is preserved/conserved because of time-translation symmetry.
I don’t know of another way. I don’t believe that Noether was the first to recognize a connection between time translations and energy, but I can’t recall the history. Nevertheless her theorem shows how general it is to link symmetries and conservation laws — both exact ones and (equally important!) approximate ones.
Though my dissertation would have been blank pages without Noether’s theorem, I had no idea it was named after a woman. Live and learn.
Not surprising that the article is so good — Ms. Angier is the best science writer I’ve ever read in a newspaper.
Thanks for discussed Noether’s theorems in your last post and again for this post about her. For a physicist, the principles of conservation are the “only” backbone for physics. Yet, I did not know Noether was the one who formulized it.
As a great physicist you are Matt, it is very difficult to disagree with you. Yet, I must disagree with your following saying this time.
Matt: “…perhaps, is that it slightly over-states Noether’s role in physics (she wasn’t as important as Einstein, but that’s hardly a criticism)…”
There is no doubt about Einstein’s greatness. His theories are definitely valid in terms of “physics”, that is, verified zillion times experimentally. Anyone doubts about this is simply “stupid”. However, I have two opinions about Relativity theories.
1. Even without the Relativity theories, physics can go on, still developing the Quantum physics and the modern particle physics although we might lack good guideline to build the accelerators. Yet, from trials and errors, we can still build it, and perhaps discovers the Relativity theories from this trials and errors efforts. Einstein’s greatness was that he envisioned the “relativities” without the experiences of building an accelerator. On the other hand, physics will be greatly handicapped without the principles of conservation.
2. While GR (General Relativity) is a valid physics theory, it nonetheless is a “failed” theory. The “goal” of GR is to be a unified gravity theory, and it failed on that goal. There are many reasons for its failure. In my view, two of them are the killers.
a. The final gravity theory must know what the “mass” is exactly. Yet, the GR put the “mass” into the theory as a prerequisite without knowing what the mass is. Then, the best the GR can do is showing that “mass” has an “attribute” of a “geometry” structure, and this is, indeed, a great insight for physics. However, this new insight was not connected strongly with his old insight that “mass” is equivalent to the “energy”. That is, the logic connection between the SR (Special Relativity) and the GR is very weak. Although they both are great theories, but they are not truly unified between the two themselves, let alone to unified “mass” and “electric charge”, which is required for a true Super Unified Theory.
b. Both SR and GR were misunderstood, even by Einstein himself.
For SR, there are two “absolutes” as the prerequisites.
i. The light speed is a Nature constant.
ii. All Inertial frames of reference are equivalent.
For GR, there are also two “absolutes” as the prerequisites.
a. The light speed is a Nature constant.
b. All “mass” is the same, the equivalence principle.
The fact is that the GR had abandoned the second requirement of SR and had chosen a “special” frame, the mass frame. This choice has two great consequences.
First, the logic connection between GR and SR is greatly weakened. Again, while GR and SR are not unified themselves (although not contradicting to each other), how can GR be a base for a unified theory?
Second, in reality, the GR is only a special case (with an accelerating frame) of SR, while this special case is named General Relativity. By naming a great theory with wrong name, we could misunderstand the context of that theory by such an error.
It is on this ground that I believe that Noether’s work is more important than Einstein’s.
I don’t agree with your statements; even if you were correct in what you say about relativity (which I must admit I completely disagree with) you perhaps have forgotten that Einstein invented the concept of a quantum (in the context of the photon) and made major contributions to quantum theory, explained Brownian motion, understood stimulated emission (which leads, down the road, to the laser), combined with Bose to predict Bose-Einstein condensates, co-posed one of the sharpest puzzles about quantum mechanics (the EPR paradox), and a number of other things. It does not diminish Noether’s achievements to say that they were less than Einstein’s, or than Newton’s, or than Riemann’s.
I’m glad you mentioned her. During her life she got screwed for far too long by narrow minded humans, despite the support of the likes of Hilbert, Klein and others. As some later screwed Jocelyn Bell Burnell.
Her life was in some ways quite tragic, especially given its untimely end. She might have had quite a good stay in the US, had it lasted. I do not know much about what her life was really like, though.