Matt Strassler [15 Jan 2012]
In this article and the next, we will learn why extra dimensions lead to “Kaluza-Klein (KK) partner” particles (described in the previous article in this series, which you should read before this one.) If a known type of particle of mass m can travel in a dimension of which we are unaware — an “extra” dimension — then we will eventually discover many other types of particles, similar to the known one but heavier, with masses M>m.
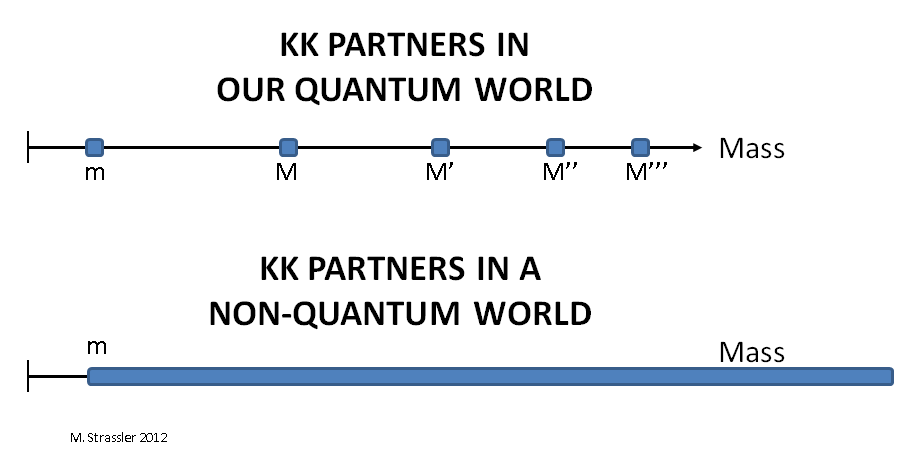
In this “Step 1” article I’m going to begin to explain to you why this is true, but I will give you only half the argument. This half will tell you why there are KK partners, and why they all have masses M > m. But this part of the argument will incorrectly suggest that there is a type of KK partner particle for every mass M that is larger than m. Only in Step 2 (the next article), when we include a little bit of quantum mechanics, will we get the right answer: that these particles come with very specific masses, a discrete set, with the first new one somewhat heavier (and perhaps much heavier) than the known one. See Figure 1.
Let’s start from a naive question about the strip — the ship canal in our previous examples, which you should definitely read about if you have not already. An observer that, like the freighter in our examples, knows nothing about the short dimension thinks the ship canal is just a line, not a strip. But if this observer is scientifically minded, he or she still knows a thing or two. First, the observer knows about motion forward and backward along the strip; velocity and momentum along the strip make sense to this observer. Second, the observer also knows about energy, and knows that energy is related to mass and motion. Specifically, a particle’s energy E is related to its mass m and its motion (in particular, its momentum p along the strip) by Einstein’s famous formula
- E2 = m2 c4 + p2 c2
which says that a particle’s energy is given by a combination of mass-energy and motion-energy. For a particle that is motionless and has therefore no momentum (p=0), this formula reduces, as it must, to E2 = m2 c4, or in other words, E = m c2 .
So if there is a small boat motionless in the canal, an observer who knows about both dimensions and observes the boat will say: Its momentum is zero, and its energy is all mass-energy: E = m c2. And an observer who knows only about the dimension along the strip will say exactly the same thing. See Figure 2, upper panel, where the viewpoint of the observer who knows about two dimensions is shown in the upper part of the panel, while the view of the observer who knows about only the long dimension, and thinks the ship canal is just a line, is shown in the lower part.
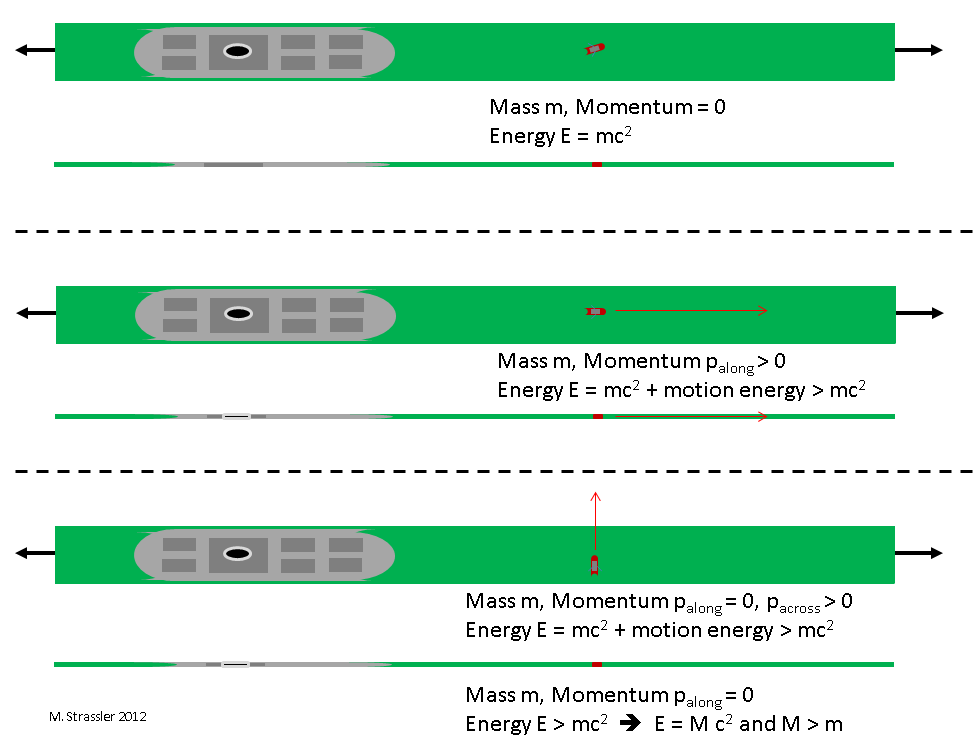
If instead the small boat is moving along the canal, an observer who knows about both dimensions and observes the boat will say: Its momentum along the canal, palong, is non-zero, and its energy-squared is
- E2 = m2 c4 + (palong)2 c2 .
And an observer who knows only about the dimension along the strip will again say exactly the same thing. See Figure 2, middle panel.
But what does an observer think he or she is looking at when studying a particle that is not moving along the strip but is instead moving across the strip? See Figure 2, lower panel.
An observer who knows about both dimensions and observes the boat will say: Its momentum along the canal, palong, is zero, but its momentum across the canal, pacross, is not zero, so its energy-squared is E2 = m2 c4 + (pacross)2 c2. Notice this means, necessarily, that E > m c2, because the boat has motion-energy as well as mass-energy.
However, an observer who knows only about the dimension along the strip cannot possibly say the same thing, because this observer knows nothing about the possibility of pacross. What the observer will think, looking at this particle, is that it is not moving. After all, it is not moving along the strip, and that is the only type of motion the observer can detect. And so, according to the observer, all of the particle’s energy, whatever it is, must be due to its mass.
So when looking at a particle that has palong=0 and non-zero pacross , the one-dimensional observer makes a mistake, but a very interesting one. This observer says: Hmmm. The momentum of this object is zero, and so its energy should be equal to its mass times c2, as was the case for the boat in the upper panel. But its energy E is larger than m c2, so this can’t be the same boat that we saw in the upper panel. Apparently nature has another type of small boat that we didn’t originally know about, similar to the first one, but with a different and larger mass: M = E/c2.
In other words, if a boat of mass m is moving with momentum pacross across the canal, the naive observer unaware of the extra dimension will incorrectly infer that what is being observed is a boat of mass M > m, with
M2 = m2 + (pacross /c)2 > m2 .
From this line of reasoning, we learn a correct piece of information: the signature of an extra dimension is the presence of particles that are similar in character to known particles (which are the particles that move only along the strip) but which appear heavier (due in fact to their unobserved motion across the strip.) And this immediately generalizes from the strip (with its one long dimension and one short dimension) to our own universe (with three long dimensions and perhaps one or more short dimensions); when known particles move in extra (i.e. unknown) dimensions, they appear to us to be heavier versions of themselves.
But the intuition we’ve obtained here is also wrong, because naively it would seem that a particle moving across the strip could have any momentum that it wants, and therefore an observer should see particles with every possible mass M that is bigger than m, as shown at the bottom of Figure 1. And that’s not correct. Instead, only very specific values of M are allowed, as shown at the top of Figure 1 — a discrete set, not the continuous set of masses that our argument would have implied. And that’s because of quantum mechanics. It’s because “particles” are actually quantized waves, or “quanta,” which was not true of the little boat used in the examples above. In the next article we’ll see why this makes such a difference.


23 Responses
I’m confused about the argument used to deduce that a 1-dimensional being on the ship will measure the energy to be greater than before.
To someone standing still outside a moving ship, the ship’s energy will be greater than its rest mass because of kinetic energy. However, an observer on the ship will consider the ship to not be moving, and will measure the energy to be equal to rest mass. If the observer on the ship can somehow tell the ship is moving and therefore has a kinetic component, isn’t that a violation of relativity?
I just realized my last question was not written well; here is the revision:
If the observer on the ship measures the ship’s energy to be greater than the original rest mass from before, isn’t that a violation of relativity? The observer would obviously think the kinetic component was zero.
Great blog, Matt. Found it while reading about Higgs. I hope you will entertain a basic question. So, it would seem that KK partner particles exist only in mathematical reality to satisfy an equation. There is no real another boat with mass M>m, the “existence” of M is based on a wrong supposition that there is no Pacross, only that E is measured to be higher. There is no experimental way to measure M of the larger boat, and so, there is no way to experimentally measure M, M’, M”… for KK partner particles because they do not exist in physical reality. How would we reconcile this with the existence of an extra dimension, which does have a physical reality?
Are you so sure that small dimensions have the same fundamental constants? — And the same fields and force carriers that we know so well? Is there symmetry or a transfer function for how the same thing “looks” from one side or the other in that small dimension?
Your question doesn’t have meaning, as stated.
Fundamental constants are not things that dimensions have — so what do you mean by asking whether “small dimensions have the same fundamental constants”?
Space is the region in which things can happen; the number of dimensions is the number of quantities needed to specify where you are.
A point or region in space can have properties such as laws of nature, constants (or local constants) that govern the behavior of physical things, etc.
But a dimension is not a point or region in space.
Think about the canal example that I’ve used elsewhere: there’s the long-dimension along the canal and the short-dimension along the canal. Can you ask whether the dimension that is associated with motion across the canal has a different electron mass than does the long direction? that’s not a meaningful question.
I can ask whether points near one side of the canal have electrons with the same mass as do points near the other side. But that’s a different question.
Before I ask my question I just want to say I found your blog by accident a short time ago and I love it. I’m currently reading your back catalog and it’s great to see such intuitive and easy to follow explanations. I’ve always had an interest in physics (debated studying it in school but went with engineering instead) and I read books by Kaku and Smolin which are great but don’t get into the nuts and bolts of things as much as I’d like them to.
Anyways, my question is, do these methods hold true for higher spatial dimensions that may be larger than the 3 we occupy? Is there a way to formulate extra dimensions larger than our 3 that are also finite, though large, in size? Would particles moving in these dimensions appear to have more mass than we predict using only 3 dimensions?
The methods I’ve described here are not unique to a world with 3 very large spatial dimensions, and nowhere have I used the fact that the extra dimensions are small. Everything I’ve said would be true if the extra dimensions I described were a millimeter, or a mile, across.
The restrictions on the sizes of extra dimensions in our world come entirely from experiment, not from theory.
Ah okay, I guess I was just making some assumptions then. So based on the experimental results there’s restrictions on the size of any extra dimensions because the KK particles would have been already for certain cases. I think I’m catching on.
So can’t the 2 higher generations in the SM be KK partners of the first generation? They do differ by mass only, don’t they?
Explained in the next article: it’s a good question, but there’s a good answer, and the answer is negative; the properties of the muon and the tau are not consistent with being KK partners of the electron.
I do not understand one point. If this picture is right, then the KK partners shall be omnipresent. They cannot decay to their lighter partners, because it breaks momentum conservation law. So either there are no extra dimensions or none of known particles can move through them.
It’s a great question… especially since I carefully avoided it here. (It will be important when we discuss how to discover extra dimensions experimentally, which I will write about in a little while!)
Your statement is roughly true [once you make a KK partner, you can’t entirely get rid of it] for a tube (see the next article http://profmattstrassler.com/2012/01/20/why-extra-dimensions-lead-to-kaluza-klein-particles-part-2-of-2/ where the tube is discussed in detail.) There momentum around the tube is strictly conserved. But even there, what will happen is that because most particles decay, most KK partners (which are, of course, just the same particles moving in a small dimension) will also decay to other particles, some of which have less or no momentum in the extra dimension. So the only particle that is guaranteed to be stable is the lightest of all the KK partners… for instance, even the lightest KK partner of the W particle can probably decay to the lightest KK partner of the photon, plus an electron and an anti-neutrino. Sometimes there may be a couple of different stable KK partners. Of course, that’s not necessarily bad. The universe has dark matter, which may well be made from a new stable particle — perhaps the KK partner of a photon? (That’s pure speculation, but not crazy.)
But the tube is very special. On a strip, you notice that a particle’s momentum is not conserved, for the same reason that a ball inside a room does not conserve its momentum when it hits the wall. It can bounce elastically, and reverse its momentum. Or it can shatter into pieces, even pieces that only have momentum perpendicular to the wall. In a similar way, quanta (which is what “particles” really are — they have wave-like properties, see the following article again) can lose momentum when there are walls around. It turns out that on a strip, a quantum’s momentum can change by an even number of units of the minimum momentum… so the 2nd-lightest KK partner can decay to ordinary particles directly, because of the edges of the strip. Only the lightest KK partner of any particle can be stable — and typically only the lightest of these avoids decay.
Finally, even the strip is special. On a complicated shape with edges, there are often no conservation laws left (imagine a ball bouncing in a strangely-shaped room — its momentum would be changing wildly every time it hit a wall) and all of the KK partners can decay to known particles.
Thank you for the answer. After reading the Part Two, I realised that my comment was irrelevant. If only standing waves are allowed on strip, than then momentum is conserved exactly in KK partners decay as standing waves carry no momentum (it is superposition of two waves with opposite momentum). I think that only standing waves are allowed on tube as well, it is somehow related to the freedom of choosing reference frame.
No, you had it right on the tube; there is a conservation law there. See my comments elsewhere about KK partners of the photons potentially being dark matter.
Thanks a lot Professor, really clear explanation. Can’t wait for the 2nd part!
Another great article and a super Focussed and fascinating educational site. I haven’t heard such an excitable, classy and lucid explanation from the giants Greene, Susskund, Smolin or Krauss. Is Matt leading up to a simple explanation of all the masses for all the standard model zoo particles.
Scientists blogging lyrically around their own succient and rigidly dry peer reviewed papers is the publishing future and a true godsend. Well done Prof Strassler.
Great stuff
Gerard Hammond,
Garvan institute of medical research, Sydney
Well, thanks, but I’m not going to give you a simple explanation for the masses of the particles in the standard model zoo — we don’t have one yet!
Very nice and intuitive!
Just started to read 🙂
There seems to be something wrong with the formula “m c2” in the text describing figure 2 …?
Fixed; thanks!