Extra Dimensions & Newton’s Gravity

Matt Strassler [June 20, 2012]

Suppose that we, and everything out of which we are made — all electrons and all atomic nuclei (and the quarks and gluons that make them up) — are free to move in three spatial dimensions, but are tethered to the wall of one or more extra dimensions, like the boat shown in Figure 3 of the preceding article that is free to move along the wall of a canal but unable to move across it. Suppose also that not only the things we are made from but all the photons (particles of light) that we see (and more generally the electromagnetic field that holds our atoms and molecules together) are stuck on the wall, as are the neutrinos that play a crucial role in the sun’s nuclear furnace and that stream in great numbers through our bodies. Our entire lives and everything we know with our senses and our technology, stuck along a wall, unable to detect through motion or sight that the world extends in a direction perpendicular to the ones that we know.

What experiment could we do to determine that this is the case — that there are extra spatial dimensions which we are unable to detect, because we are tethered at one side?  And how big could such extra dimensions be?

The precise answer depends on the shape of space — the shape of the extra dimensions, certainly, and more generally on the shape of all the dimensions put together. That probably sounds very cryptic, but I’ll gradually try to give you some feel for what this might mean.

The first step along this road is to learn something about why Newton’s law of gravity says that the gravitational force between two massive objects [slow-moving, compared to the speed of light, and not too compact — so that we don’t have to worry about Einstein’s corrections to Newton’s law] is inversely proportional to the square of the distance between them. We must also learn why the same dependence on distance also applies to the force between two electrically charged objects, Coulomb’s law. The reason for this dependence is purely geometric. And this implies in turn that we can learn about the geometry of space by studying Newton’s and Coulomb’s force laws! (Most of the other force laws in nature turn out to be affected by other issues and are not quite as good for this purpose; long story.)

It is possible (not that Newton or Coulomb knew this — it was understood in the mid-19th century) to compute the distance dependence of the gravitational and electrical forces between two objects a distance L apart using a remarkably simple trick (which doesn’t work without some additional conditions — we’ll see a couple of them later.) Here it is:

• Take one of the two objects;
• Draw a surface surrounding one of the objects that lies at a constant distance L from the first object;
• Measure the “surface area” A of that surface (we’ll see in a moment that you have to understand the word “area” with some flexibility here.)
• Then if the surface is nice and symmetric, the strength of the force is inversely proportional to that area!

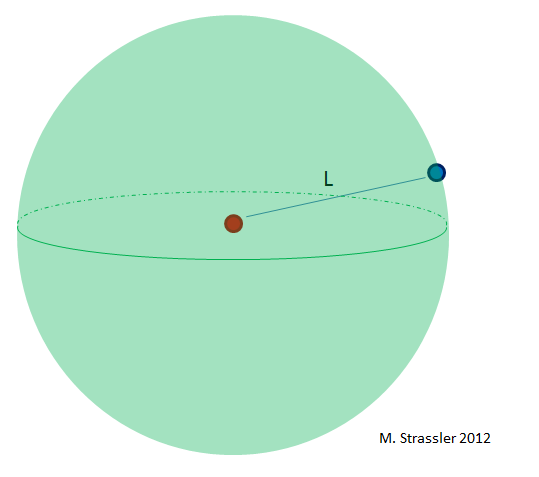
This is the simplest version of what is called Gauss’s law. Let’s check it.

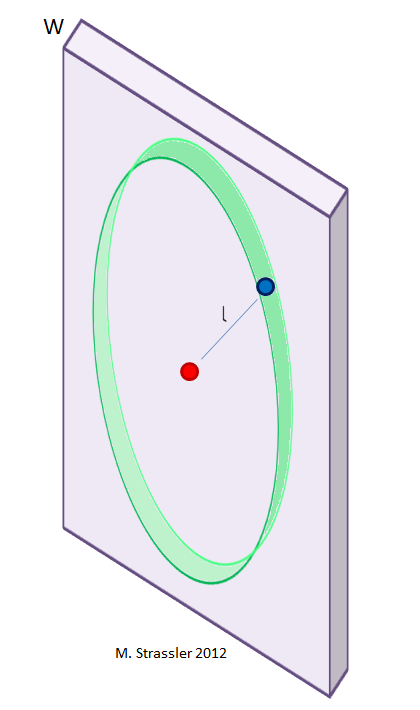
In Figure 1 is an object in red, and an object in blue a distance L away. (Just to be absolutely clear: this is a picture meant to represent ordinary three-dimensional space, with three dimensions of infinite extent.) Let’s draw a surface that contains all the points that are a distance L away from the red object: that’s a sphere, of radius L. That’s the greenish sphere in Figure 1.

• What’s the area of the sphere? 4 π L²
• What’s the force law? It is inversely proportional to L².

And again, this is true for both Newton’s law of gravity and Coulomb’s law of electrical forces. It’s a purely geometric effect.

Suppose we lived in a world that had only two spatial dimensions, such as the one drawn in Figure 2. Then the same calculation would tell us that we should draw a circle of radius L around the red object. What is the “surface area” of this circle? The idea of surface “area” mentioned above implicitly means that we should measure the size of the edge of the surface — in the case of a sphere, that was the area of the outer surface of the sphere, whereas in this case it is the perimeter of the circle we should measure.

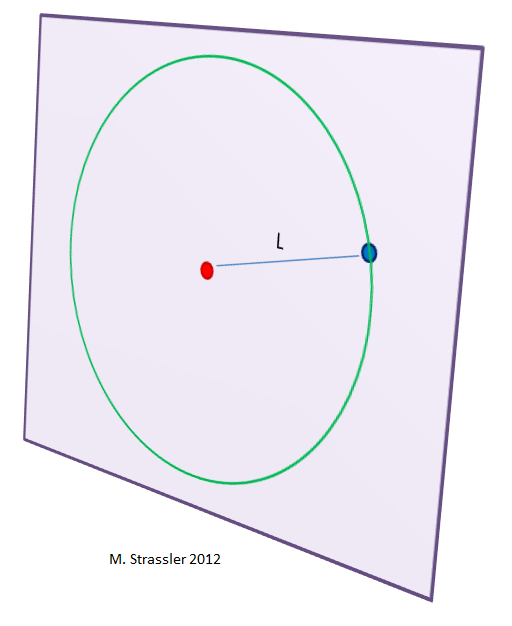
• The perimeter of the circle is 2 π L.
• Therefore the force law is inversely proportional to L.

This would be true both for gravity and for electrical forces in a two-dimensional world.

Now you can guess what the answer would be in a world with 4 spatial dimensions. In a world with 4 spatial dimensions, the surface surrounding the red object would be 3 dimensional, and so its “surface area” would be proportional to L³, and gravitational and electrical forces would be inversely proportional to the cube of the distance between the two objects. And so on: if we lived in a world with D spatial dimensions, these force laws would be inversely proportional to (L)^D-1.

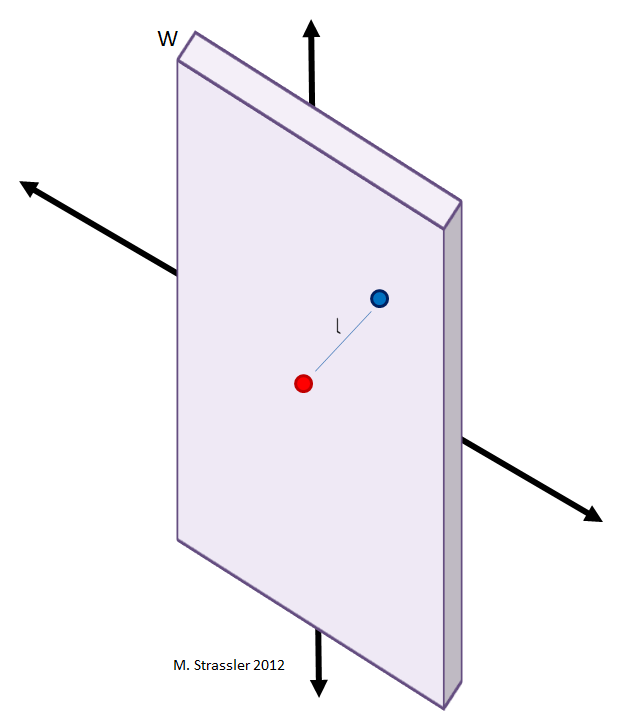
All along here I’ve assumed that all the dimensions are infinite (or so big that their size doesn’t matter for any practical experiments.) But the case we were interested in is the one were 3 dimensions are infinite or very large, and some number n of them are finite in size. What happens to the force laws in that case?

To get a feel for this, let’s do the case where 2 dimensions are infinite and one dimension is small in size. This is the case where the universe has the shape of a slab, like the interior of a table top, as shown in Figure 3.

Now what is the shape of the surface containing all points a distance L away from the red object? Well, that depends on how large L is relative to the width W of the slab.

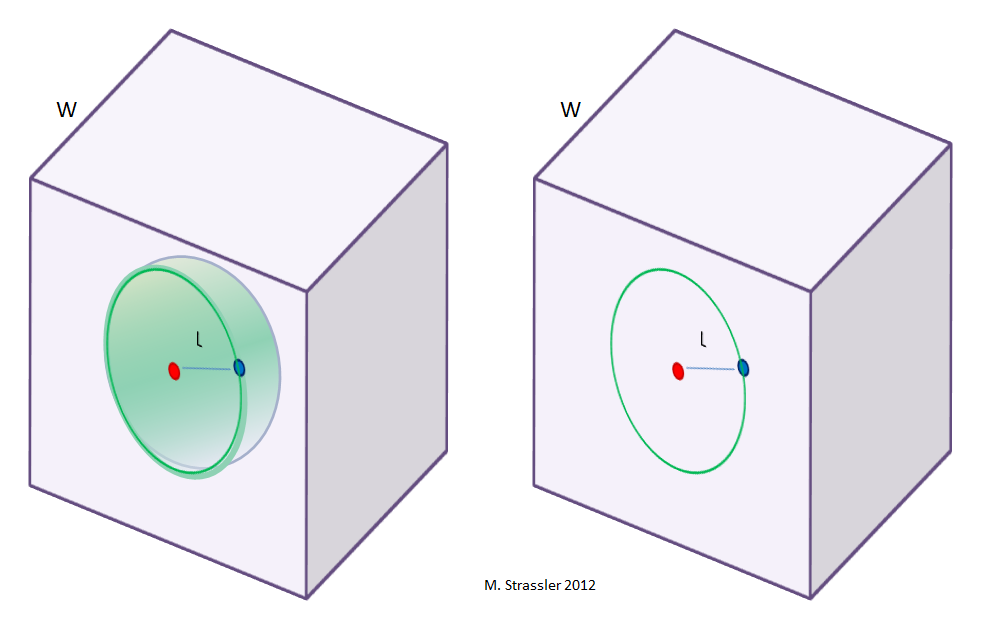
• If L is much smaller than W, the shape of the surface is a sphere, which fits easily inside the slab (Figure 4). Its surface area is 4 π L².
• If L is much larger than W, the shape of the surface is a ribbon (Figure 5), of width W, in the form of a circle of radius L.
  Its surface area is 2 π L W.
• If L is about the same size as W, the shape of the surface is complicated, so we cannot use our trick for calculating the force law.

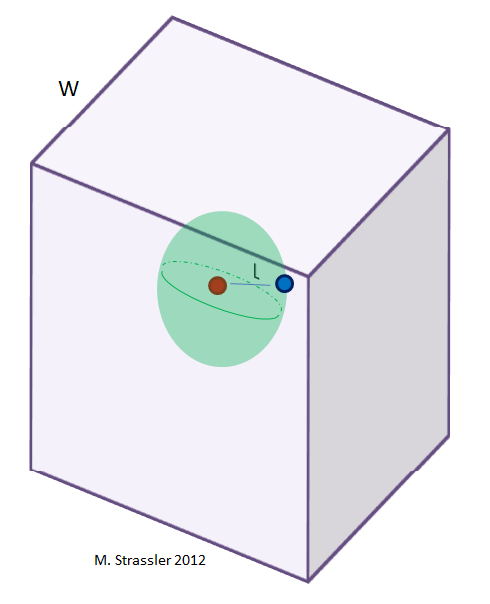
From this we learn that the force law is

• Inversely proportional to L, if L >> W;
• Inversely proportional to L², if L << W;
• Something a bit complicated if L and W are about the same size.

And so we learn how, if we were apparently two-dimensional creatures living inside the slab of microscopic width W, we might prove that the world is in the form of a slab as follows: perform careful measurements of electrical or gravitational forces and show that although at very long distances the force laws are proportional to 1/L, and microscopic distances something changes and the force law becomes 1/L². And the value of L where the force law changes would then give us an estimate of W, the width of the previously unknown extra dimension. Conversely, if we saw no change in the law, that would tell us W had to be smaller than any L down to which we could perform the measurement.

Now let’s add a dimension. We are apparently three-dimensional creatures; but suppose we are living inside a (3+n)-dimensional slab of width W? How could we find out? Answer: measure Coulomb’s law for electric forces and/or Newton’s law for gravitational forces very carefully, at as small L as possible. If we measure the force to be

• Inversely proportional to L², for large L;
• Inversely proportional to L²⁺ⁿ, for small L;

with a transition between the two at L ~ L₀, then that would suggest that there are n additional dimensions with a size W ~ L₀. And conversely, if NO deviation from the 1/L² force law is observed for L ~ L_min, then that tells us there are NO extra dimensions with a size W > L_min.

Now, what do we in fact know about electric and gravitational forces? About electrical forces we know a great deal via this method. (Let’s go through the argument, but keep in mind that the absence of Kaluza-Klein partner particles of the photon, discussed here, is an even more powerful test for the absence of extra dimensions affecting the electric field.) These forces hold atoms together and the details of all our atomic physics calculations depend crucially on the 1/L² law being correct down to about the size of a typical atom. Electromagnetic effects on nuclei aren’t as important, but still we would see big effects on nuclear physics if the force law for electric forces changed a lot. So all of this indicates that electrical forces can’t vary significantly from their three-space-dimensional form down to something like few tens of millionths of a billionth of a meter, a bit larger than the typical atomic nucleus.

About gravity, however, we know much less. So weak is gravity that the gravitational forces between elementary particles cannot be measured. Technically, precisely measuring the gravitational forces between small and close objects, without getting confused by the effects of stray electrical forces, proves very difficult. The smallest L for which anyone has managed to test Newton’s 1/L² law for gravity is about 0.000 03 meters (30 micrometers, or 30 microns, or about one thousandth of an inch.) In short, we only know that gravitational forces can’t vary significantly from their three-space-dimensional form down to something like few hundred thousandths of a meter, or a bit larger than the typical human hair!

So now it is time to return to the possibility that we and everything we are made of and everything we see and everything that affects us — except gravity — are trapped on the wall at the edge of an extra dimension.

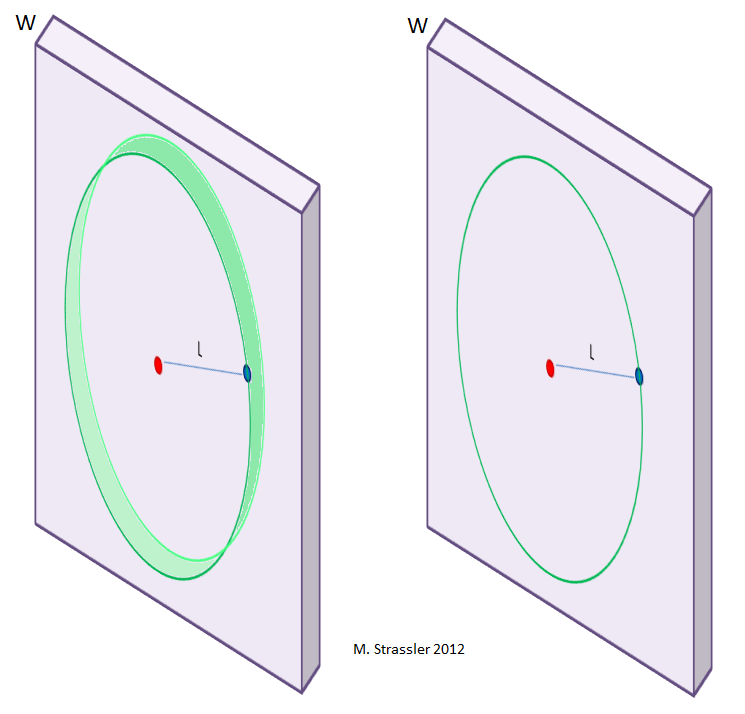
First, imagine we are two-dimensional creatures living in a trapped on a two-dimensional side of a three-dimensional slab, as shown in Figures 5 and 6.  What will we find for the forces between two objects? Because electric fields are trapped on one side of the slab, we will calculate them by drawing a circle around the red disk that passes through the blue disk, as we did in Figure 3, and they will give the two-dimensional force law 1/L for any L no matter how small.   (See Figures 5 and 6, right-hand side.) They are completely insensitive to the presence of the extra dimension across the slab. But gravitational fields, not being trapped on the wall of the slab, will take a more complicated form. Why? Because for large L >> W the gravitational force between the red object and the blue object will be computable using the ribbon in the left-hand side of Figure 5; but for small L << W the gravitational force between the objects must be calculated by drawing a half-sphere around it (Figure 6, left-hand side), extending around it; and the area of that half-sphere (half the radius of the corresponding sphere) is 2 π L², as long as L is much less than W. In short, in this imaginary world, we will find

• Electric forces are inversely proportional to L, for all L;
• Gravitational forces are inversely proportional to L, if L >> W;
• Gravitational forces are inversely proportional to L², if L << W;
• Gravitational forces are a bit complicated if L and W are about the same size.

Conversely, if we see gravitational forces inversely proportional to 1/L down as far as we can measure, that (in this imaginary world with two dimensions of infinite extent) tells us that there is no extra dimension of a size larger than the smallest experimentally accessible L.

Ok, what about the realistic case, where we are apparently three-dimensional creatures who might be trapped in a three-dimensional wall with n extra dimensions around us? (See Figure 4 of the preceding article for a reminder about some of the various geometric options.) If all known particles (including photons) and their corresponding fields (including electric fields) are trapped on the walls, but gravitons and gravitational fields are not, and if the widths of the extra dimensions are all about W in width, then we expect

• Electric forces are inversely proportional to L², for all L;
• Gravitational forces are inversely proportional to L², if L >> W;
• Gravitational forces are inversely proportional to L²⁺ⁿ, if L << W;
• Gravitational forces are a bit complicated if L and W are about the same size.

So the fact that Newton’s law for gravity has been measured to hold down to 0.000,03 meters tells us that if there are any extra dimensions of this type, they must be smaller than about 0.000,03 meters. That may sound small, but remember that is many tens of thousands of times larger than a water molecule! On the atomic scale, it’s huge! and yet the effect of this type of enormous extra dimension on atomic physics would be too small for us to measure. (In fact, until around the year 2000 or so, the best measurements only tested Newton’s law down to a millimeter [0.04 of an inch!] The improvements in the measurements of gravitational forces were motivated, at least initially, by the work of Arkani-Hamed, Dimopoulos and Dvali, who in 1999 shocked the particle physics community by pointing out that the possibility of millimeter-sized extra dimensions was consistent with all existing data.)

A comment: I’ve focused on the case where we are trapped at one side of the extra dimension.  It is possible to be trapped on a wall that cuts down the middle of the slab (parallel with the exterior walls but at some distance from them.)  The arguments I’ve given here need only minor adjustment; the conclusions about the force laws don’t change.   (The details of what the gravitational force law does for L ~ W could be used to help determine the precise shape of the slab and the location of the region on which we are trapped.)

Another comment: I’ve assumed here that the geometry of space is very simple, so that the properties of the three dimensions we know don’t depend on where we are in any of the extra dimensions. If I relax that assumption, things can get more complicated. In particular, there is a loophole which allows the extra dimension to be much larger than 0.000,03 meters, but only at the expense of making it even harder to move in that direction. We’ll get back to this possibility of “warped extra dimensions” — the work of Randall and Sundrum — later.

First, let’s see that there are (in many cases) more powerful limits, coming in an indirect and tricky way from Kaluza-Klein partner particles of the graviton itself.

Kaluza-Klein states for gravity. [coming soon]