Transit of Venus and the Distance to the Sun

Much has been written and is still being written about the 2012 transit across the Sun by Venus. You can read in many places (here’s a good one) about how rare this transit is, and why it is so rare: naively Venus, which circles the sun more rapidly than does the Earth, should pass between the Earth and the Sun once every orbit (Figure 1), but because the orbits of the two planets are not well aligned (Figure 2) Venus often appears to pass above or below the Sun from the Earth’s perspective.

Rather than rehash what so many have written about, I wanted to add a few little details that aren’t so easy to find on the internet.

You may have read that with a technique based on earlier reasoning from 1678 – 1716 by astronomer Edmund Halley (of Halley’s Comet fame) and James Gregory before him, the transit of Venus in 1761 was used to determine the distance from the Earth to the Sun (and to Venus and all the other planets) with to a precision of about 2 percent, by far the highest precision yet obtained. (It had been hoped the measurement would be about ten times more precise, but an unexpected optical effect, called the “black drop effect”, whose cause still generates controversy, interfered.) But you may not have read that this measurement was based — as are so many measurements of distance in astronomy, out to the relatively nearby stars — on the principle of parallax, the same geometrical fact used by our eyes and brains to produce depth perception, our ability to tell how far away objects are just by looking at them.

Without parallax, it isn’t hard to figure out how far Venus is relative to the Sun — that is, to determine the ratio of the radius of Venus’s orbit L_V to the radius of Earth’s orbit L_E. That’s why it was widely understood quite early in Renaissance astronomy what the relative distances were from the planets to the Earth and to the Sun.  But to determine  L_V and L_E separately requires a parallax measurement, and a transit of Venus can provide a good one.   The transits of Venus in the 1760s provided a rather precise measurement of L_E – L_V , the “absolute” distance from Earth to Venus; and that allowed L_E and L_V and the distances to all the other planets to become known, to a precision of a couple of percent.   (There was an earlier measurement of the distance from Earth to Mars that was precise to about ten percent, made in the late 1600s; this too was based on parallax, but that’s another story.)

One preliminary point: The Earth and Venus, and even the Sun, are so small compared to the distances between them that drawing pictures that are really accurate is basically impossible. When making pictures that illustrate what is going on, it is always necessary to make the planets look bigger than they are, relative to the distances between them, just so you can understand the important conceptual points being made. Do keep this in mind! None of my pictures below are to scale — they can’t be.

Here we go.

The Relative Size of Venus’ Orbit Compared to Earth’s Orbit

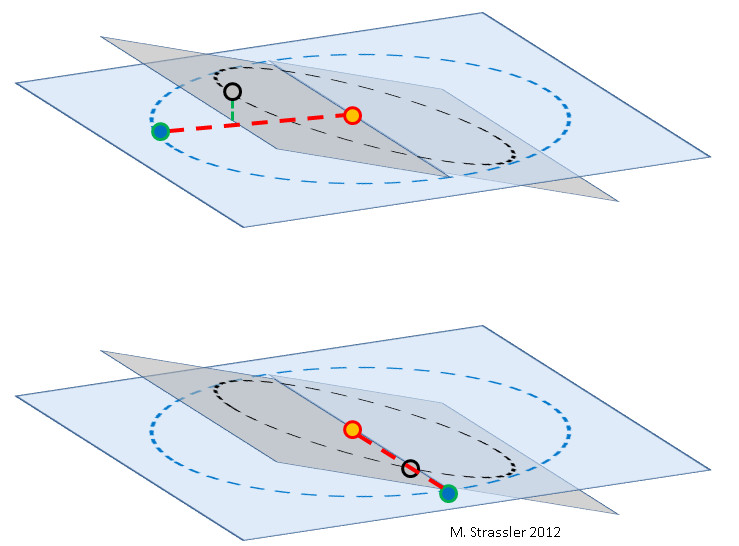
To understand the basic reason why it is easy to determine L_V/L_E , we’re going to assume, for the purposes of making an estimate and seeing the basic principles involved, that the orbits of Earth and Venus around the sun are circular and that they are aligned — that they lie in the same plane (shown in slanted perspective in Figure 1, and from directly “above” in Figure 3). In fact the orbits of Earth and Venus are slightly elliptical and they are not perfectly aligned (Figure 2), and as noted earlier this explains why transits of Venus are rare. But the ellipticity and non-alignment are minor points for the following argument, so we can ignore them initially, and put them back in later to get more accurate answers (which I would do, carefully, if I were teaching a class for future experts, but won’t do here as it doesn’t add much conceptual understanding.)

What we’re doing here is a physicist’s classic technique; make an approximation that is sufficient for current purposes, and don’t work harder than necessary.  It’s a very powerful way of thinking about science, and about knowledge in general — any question you ask only needs to be answered to a certain degree of precision, so use the simplest technique that gets you the answer to that level of precision.  This method’s been used for centuries, to great effect, and it applies far beyond physics.

So we’ll make the approximation that the orbits are circular and aligned, and the answers we’ll get will be approximately correct, to a few percent. That will be enough to illustrate the basic conceptual principles involved, which is my current goal.   You can trust me that it’s possible to make a much more accurate and precise calculation, or you can become an expert and figure it out for yourself. But the approximation used here will not only give a pretty good answer but will be enough to show you why it is easy to figure out the ratio of L_V to L_E, but not to figure out L_E or L_V separately.

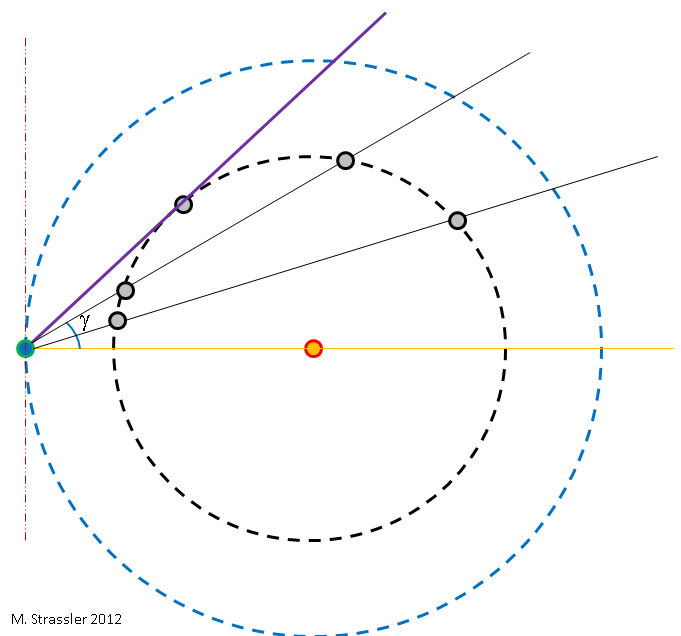
During the year, as Earth and Venus orbit the Sun at different rates, the relative positions of Earth and Venus change relative to the Sun. If, on a particular date (day, month and year), I choose to draw a picture with the Sun at the center and the Earth off to the left, as in Figure 2, then Venus may be anywhere in its orbit, depending on the date. And that means, relative to Earth’s point of view, the angle between Venus and the Sun in the sky will vary, depending on the date. This is shown in Figure 3, where the angle is called γ. The angle is easily measured; find Venus is in the sky just after sunset or just before sunrise, and measure the angle between Venus and the Sun; see Figure 4.

What you can see from Figure 3 is that γ has a maximum size, shown by the angle between the orange line and the violet line.  As it travels in its orbit, Venus will appear in a different location at each sunset; for a while, night after night, it will be in a higher location above the horizon, and then eventually begin to fall back toward the horizon.  By watching Venus night after night, just after sunset, and measuring γ night after night, we can determine the maximum value of γ, which I’ll call γ_max.

It’s obvious from Figure 3 that (as drawn in Figure 4) γ_max is less than 90 degrees, because the violet line must lie between the orange and red lines, which are perpendicular. You can see geometrically that this is a consequence of the fact that Venus is always closer to the Sun than is the Earth.  These angles explain why Venus is always visible either just after sunset or just before sunrise (except for the few days when it lies in front of or behind the Sun.) Venus can never be directly overhead after dark, for this would require it to lie to the left of the red line, which it can never do.

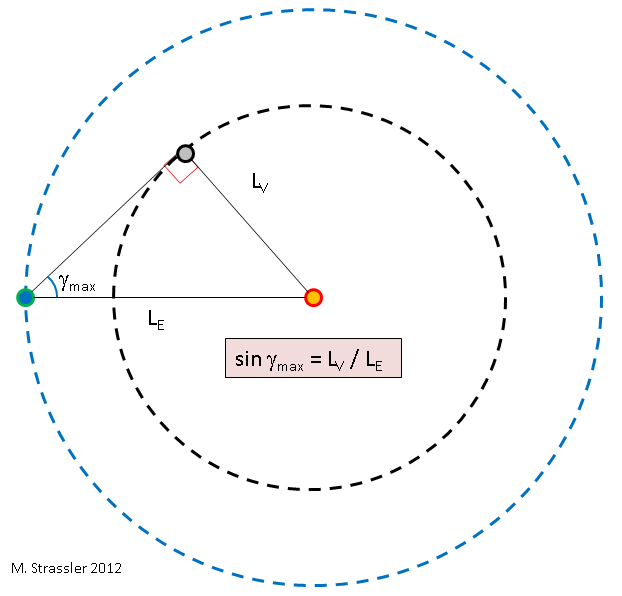
Now — we can determine the ratio of the radii of the two orbits — of L_V to L_E — using  γ_max.   It’s simple geometry, Figure 5. The point is that when Venus is at its maximum angle from the Sun, the line from the Sun to Venus is perpendicular to the line from the Earth to Venus, and so the lines joining the three objects form a right-angle triangle. From this we obtain, using standard trigonometry, that

• L_V/L_E = sin γ_max.

And from this (and other simple geometric arguments) we get the ratios of all the distances to the other planets.

Again, this isn’t exactly right, for the reasons mentioned at the start; the planetary orbits are ellipses, and the ellipses don’t lie in the same plane. In other words, L_E and L_V aren’t exactly constant over the year, and γ_max is actually something more complicated that has to be thought about in three dimensions, as in Figure 2, not two dimensions as in Figures 1, 3 and 5. But with precise measurements over many years of the positions of Venus and the Sun in the sky, it is possible to determine the precise orbits of Venus and the Earth around the Sun, and improve the argument. The main point is the same; all of the measurements of the location of Venus and the Sun in the sky allow only a measurement of the relative sizes of the orbits of Venus and Earth. But the overall size — the actual values of L_E and L_V — cannot be determined. A different method is needed.

The Transit of Venus, Parallax, and the Distance to the Sun

If you aren’t familiar with parallax already, or just want a review, you can read my article on parallax.

The reason that a transit of Venus allows for a measurement of the absolute size of the Earth’s orbit and Venus’s orbit is that the transit of Venus can be observed with precision at different locations on the Earth, giving two different high-precision perspectives on the apparent location of Venus relative to the Sun, taken from positions that are separated by a known distance. This parallax measurement (a bit of a tricky one) in turn allows the absolute distance from Earth to Venus to be determined from the parallax angle and the distance between the two observing points on Earth, just as the different views of an object from our left and right eyes allows our brains to provide us with depth perception — a sense for how far away the object is.

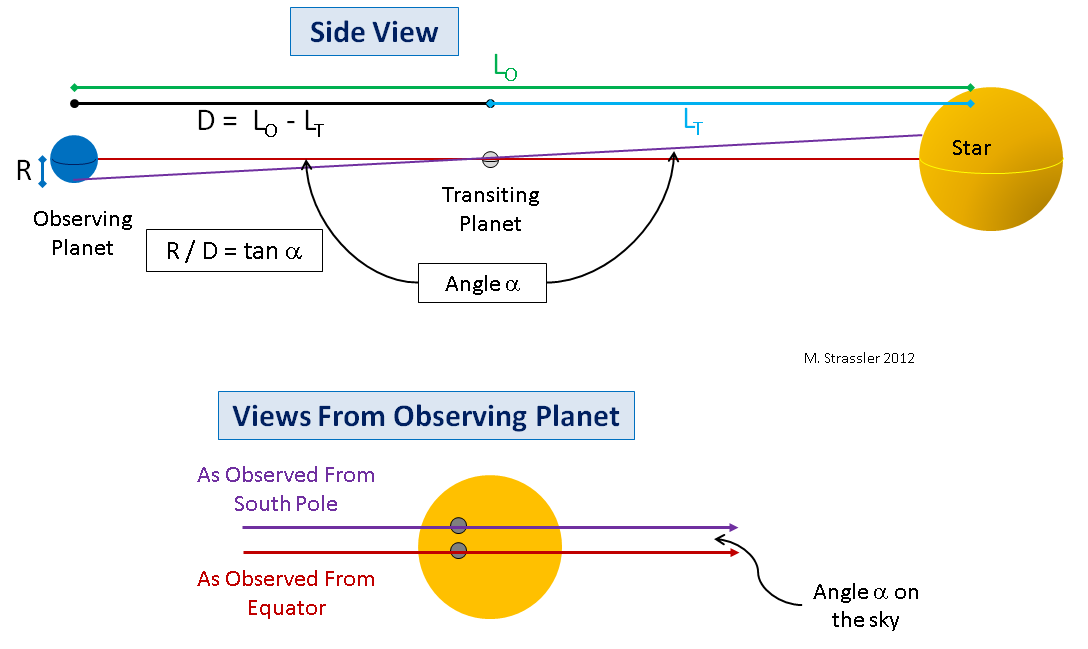
To illustrate the point, let me draw how this would work with large planets so you can see in a figure what’s going on. In Figure 6 I show a planet where a transit is to be Observed (later to be the Earth), and a planet that’s Transiting (later to be Venus), in front of a star. And I’m going to imagine the simplified situation (just to make the geometry more obvious and the basic point easier to visualize at first) where the planets and the star are perfectly aligned (which will not be the case for this year’s transit) so that from the point of view of someone on the equator of the observing planet, the transiting planet will appear to move along the equator of the star. This is shown from the “side” at the top of Figure 6; note the red line from the equator of the observing planet to the star, passing through the equator of the transiting planet.

With this perfect alignment, an observer on the equator of the outer planet will see the inner planet traverse the equator of the star.  This is shown as the red curve in the lower part of Figure 6.  But an observer at the south pole of the outer planet will see the inner planet traverse the star on a path (violet line) that lies north of the star’s equator. (The reverse would be true at the north pole.) If the angle α on the sky between the paths taken by the transiting planet, as seen from the equator and the pole of the observing planet, is measured, and the radius R of the observing planet is known, then we can draw a right-angle triangle that connects the transiting planet, the center of the observing planet, and the pole of the observing planet, whose small angle is α. Simple trigonometry then tells us that the two planets are a distance D apart during the transit, where

• D = R / tan α

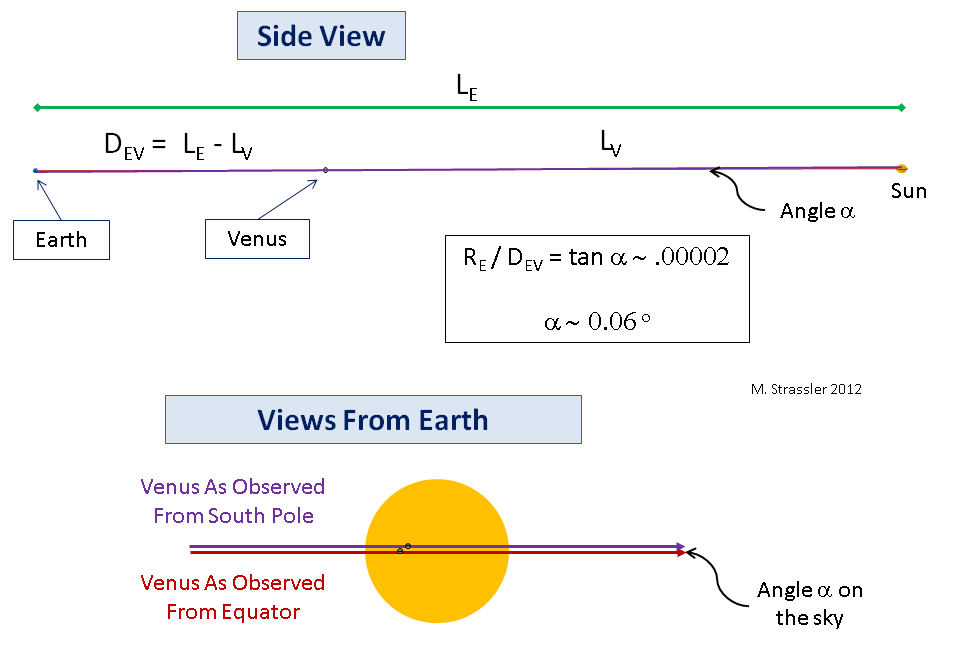
Now the same applies for the Earth, Venus and the Sun, except that the Earth and Venus are so small, and the distances between them and the Sun so vast, that it turns out that the angle α would be only about 1/20th of a degree! (That’s quite tiny but also quite measurable, but to measure the distance to the Sun precisely, as 18th century astronomers hoped to do, would require a very precise measurement of this tiny angle, which is not so easy.) That’s far too small an angle for me to draw, so you have to trust me that what actually is happening is just a very extreme version of what I drew in Figure 6, with the planets and the star (the Sun, of course) much smaller than I drew them, relative to the distances. Even what is shown in Figure 7 still makes the planets look far larger than they are. But the idea is the same: the distance D_EV between the Earth and Venus during the transit can be determined be measuring the parallax angle α, (bottom of Figure 7; note the sun’s angular diameter is about 1/2 of a degree).

Now there are all sorts of unanswered questions here.

• I’ve told you how to measure D_EV, the distance from the Earth to Venus during the transit. But wasn’t the goal to measure L_E and L_V, the distance from Earth to the Sun and from Venus to the Sun?
• Nobody went to the Earth’s south pole to watch Venus transit the sun in 1761 or 1769.
• I assumed the Earth, Venus and the Sun were perfectly aligned, so that a point on the equator of the Earth would see Venus moving across the equator of the Sun. But that certainly isn’t the case, and isn’t even that close to being the case during a typical transit (and it won’t be in 2012, in particular).
• The angle α is small enough that it is hard to measure precisely — especially since, in the days before photography and instantaneous communication, and lacking a clear indication of where is the Sun’s north pole, ensuring a precise comparison of two measurements of Venus’s path made at two very different locations on the earth would have been very challenging indeed. Yet the original goal was to measure the angle to better than 1 part in 500 (though this was set back to 1 part in 50 by the “black drop effect” mentioned earlier.)

Ok, so how do we get around these issues?

First, how do we go from a measurement of D_EV to a measurement of what we want, L_E and L_V? That’s easy, because we already know all the ratios — in particular we already know L_E/L_V (approximately, from Figure 4, or more accurately, if we do our astronomy more carefully) from the maximum angle γ_max between the Venus and the Sun as seen from Earth. We also have D_EV = L_E – L_V = L_E (1-L_V/L_E), from Figure 7. So we can get an (approximate) measure of L_E by using

• L_E = D_EV / (1 – L_V/L_E)  =  R / tan α / (1 – sin γ_max)

where α is the parallax angle measured during the transit and γ_max is the maximum possible angle between Venus and the Sun (Figure 5). Doing it more precisely involves more elaborate geometry, but the basic ideas are the same.

Second, even if the alignment between the planets and the Sun were perfect, the two measurements of Venus’s path don’t have to be made at the equator and either pole of the Earth. They can be made at any two latitudes on the Earth. The geometry gets a tiny bit more complicated, but not much, and the principles remain the same.   See Figure 8.

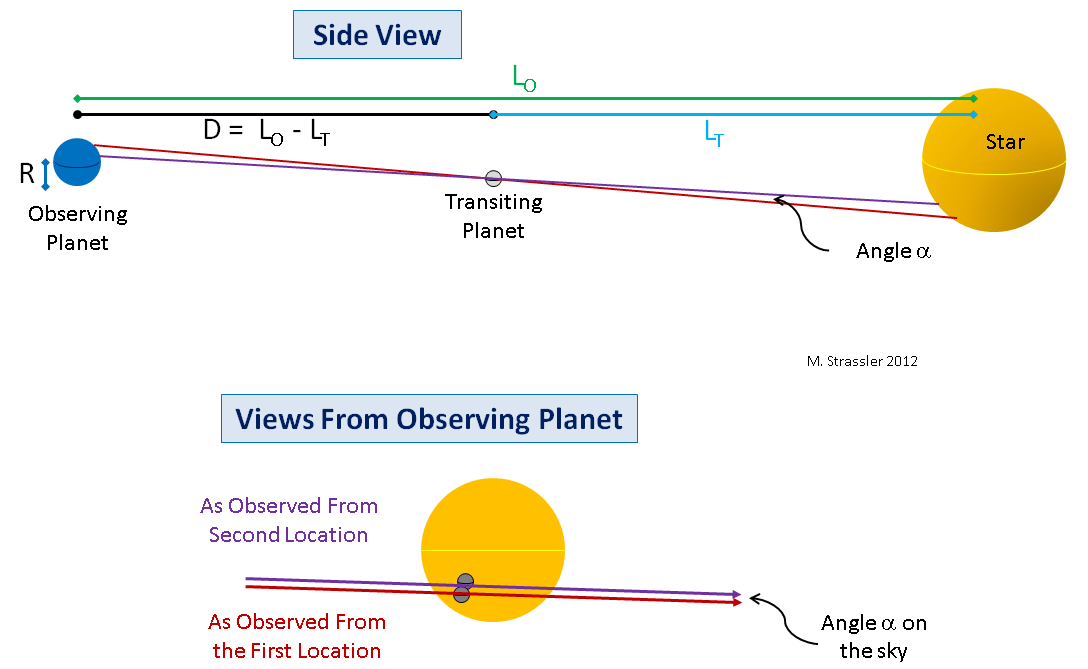
Third, even without perfect alignment, there will still be a small parallax angle that arises when the measurements are made from two different points on the earth, and if that angle can be measured well, it can be turned (through somewhat more complicated equations) into a measurement of D. This point is also illustrated in Figure 8, at bottom.

Now the fourth issue — the challenge, especially historically, of measuring the angular shift α in the path of the Venus’s transit, is one which leads us to an alternative attempt to try to measure timing — either the duration of the transit, or just the time at the start or the end of the transit — rather than angles. The first was apparently proposed by Halley, based on earlier ideas of Gregory, and the latter was suggested as a further refinement by Delisle. (Halley’s method did not require different locations to have synchronized time; Delisle’s later method did require it, and thus relied on more advanced clock technology.) It’s much easier to make a precise measurement of duration — even back in the 17th or 18th century — or of the moment of the beginning and end of the eclipse — than to precisely measure the location of Venus relative to the Sun’s disk, especially without photography. You can see that the purple and red paths of Venus crossing the sun are of slightly different lengths, because of the fact that they are not crossing the sun at the same location, and that means that duration of the transit will be different by an amount related to the parallax angle. Unfortunately things are more complicated than they look at first — because the Earth is rotating, and moving around the Sun, which means that a given observer is moving a considerable distance while Venus is transiting the Sun. So it takes some real effort (somewhat complicated and tricky, though very easy with modern computers) to determine the difference in the timing of the start and end of the transit that two different observers on the Earth will detect, depending on the distance to the Sun. Halley, at the turn of the 18th century, already understood all of the geometric principles involved (and if you subtract the dated English phraseology and style from his text, you may be impressed by the modern-sounding sophistication of his statements, and you will see that scientists of three hundred years ago were in many ways much like scientists today, possessed of the same intellect and lacking only scientific technology of the present.)

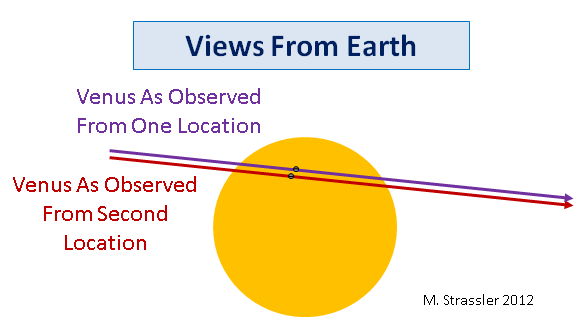
All this is to say that parallax — that difference in apparent location that observers at a particular time but at different locations on Earth will ascribe to Venus relative to the Sun — was historically an important method by which the overall size of the solar system was determined. Today there are more powerful methods available, but you can enjoy knowing that what you see in the skies today has great historical significance… or you can simply enjoy the vision of Venus proceeding in its stately motion around our star.