© Matt Strassler [April 30, 2022]
Please feel free to point out errors or suggest improvements; this is a dynamic document.
This page is the second of several (first one is here) that together will explain the “Triplet Model”, a very simple method for shifting the W boson mass upward relative to the predictions of the Standard Model.
Particles
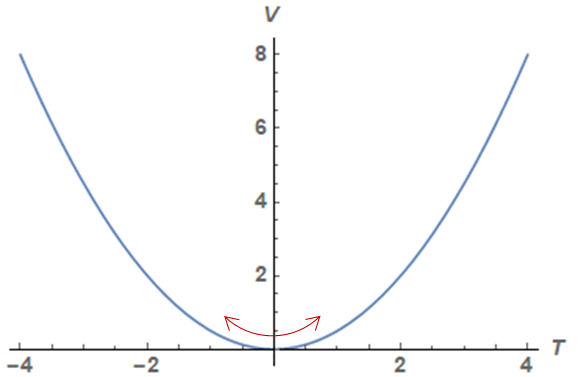
A particle is simply a tiny ripple in a field. For example, suppose we have a field T with potential
- V = ½ mT2 T2
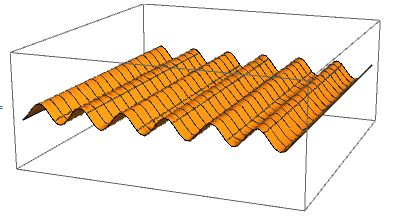
A particle will correspond to a ripple in space that moves with time, as in
- T(x,y,z,t) = f(x,t) = a cos([E t – p x] / ħ)
where the cosine function gives us a ripple moving in the positive x direction, and a, E, p and ħ are constants:
- E is the particle’s energy (all of its energy, not just its motion-energy);
- p is the particle’s momentum (and the speed of the particle is pc2/E);
- a is the amplitude of the ripple (fixed by details of quantum physics but unnecessary here);
- ħ, Planck’s constant, is a fundamental constant of nature.
[A sine function would work just as well as a cosine.] In this formula, E/ħ, which multiplies t in the cosine, determines how the ripple changes with time; the larger is E, the quicker the time dependence. Similarly, p/ħ, which multiplies x, determines the space dependence of the ripple; the larger is p, the quicker is the x dependence.
When we substitute this into the equation of motion (which I’ve now written more carefully, so as to get the units right)
- [(time variation of F)2 – c2(space variation of F)2] = – [c4 / ħ2] the variation of V with F
where c is the cosmic speed limit (a.k.a. the speed of light), we obtain
- [ (E2 – p2c2)/ ħ2 ] f(x,t) = [c4 / ħ2] mT2 f(x,t)
which is true as long as
- E2 – p2c2 = (mT c2)2
This is the formula that relates the energy E and momentum p of a particle of the field T to its rest mass mT. Notice that for p=0, we get E = mT c2, Einstein’s formula relating energy to rest mass for a stationary T particle.
We learn from this that when we see a term ½ mT2 T2 in the potential, that’s an indication that the T particle, a ripple in the T field, has a mass mT.
We might consider a more complicated potential, such as
- V = + ½ mH2 H2 + ¼ λ H4
The vacuum of this theory has <H>=0, which I called the “unbroken phase” in the previous discussion of this potential. If we put a ripple like the one we used earlier into the equation of motion, it won’t quite work, because the equation of motion will have a term proportional to H3 , and thus the ripple will appear cubed in the last term:
- (E2 – p2c2)/ ħ2 f(x,t) = mH2 [c4 / ħ2] f(x,t) + λ [c4 / ħ2] f(x,t)3
The last term would seem to mess everything up, and in fact it does; our ripple does not solve this equation.
But it almost solves it as long as f(x,t) is extremely small… and that’s the case here. To have just one H particle, we need to take the amplitude a really small. As long as λ is small too, then λ [c4 / ħ2] f(x,t)3 will be tiny compared to the other terms in the equation. (This is because if a number x << 1, then x3 << x.) The consequence of being an almost-solution to the equation, rather than a true solution, is that our ripple may or may not live forever, but it will still live for a long enough time to be meaningfully described as a particle.
However, something quite different happens in the broken phase, for which
- V = – ½ μH2 H2 + ¼ λ H4
where μH2 > 0. If we follow the logic above, a ripple in the H field of the form H = a cos([E t – p x] / ħ) would seem to have mass equal to the square root of (- μH2 ), a negative number. Would that mean the H particle’s mass is imaginary?
Tachyons?
A particle with an imaginary mass is called a tachyon. The equation of motion for a tachyon implies that E2 – p2c2 = (mT c2)2 < 0. With energy less than its momentum (times c), such a particle naively travels faster than the cosmic speed limit. That doesn’t sound very healthy…
… and in fact, it is not. We have made a mistake. In one of the vacua of the broken phase, < H > = μH /λ1/2 . In that vacuum, we should not be looking for a particle to be a ripple of the form H = a cos([E t – p x] / ħ), as we did earlier. That would be a ripple around H=0, a field that is constant, uniform and zero.. Instead we must look for a ripple of the form
- H = <H> + a cos([E t – p x] / ħ) = μH /λ1/2 + a cos([E t – p x] / ħ)
so that it is a ripple around the actual vacuum, where the field is constant, uniform and non-zero. When we do this, we find no tachyon.
The standard way to see this is to shift H, by writing
- H(x,y,z,t) = < H > + h(x,y,z,t)
where < H > is a constant, h is the shifted H field, and <h> = 0; the ripple we want will be a cosine in h. Traditionally, since “< H >” takes up a lot of room, physicists often replace < H > with “v” to stand for “vev”. So let’s say
- H = v + h
where v is a constant, H is the original field, and h is the shifted field. Then
- V = – ½ μH2 (v+h)2 + ¼ λ (v+h)4 = – ¼ μH2 v2 + μH2 h2 + λvh3 + ¼ λh4
Remember this is the same potential as before, simply rewritten in terms of h instead of H!
In this new form, the first term is a constant and plays no role in determining the vacuum. The term proportional to h vanishes exactly, so <h>=0 is indeed the vacuum. Since the h2 term in this potential has a positive coefficient +μH2 , a ripple in the H field around the true vacuum H = v has a positive mass (√2 μH) as it should, not an imaginary one. There is no tachyon in the real vacuum.
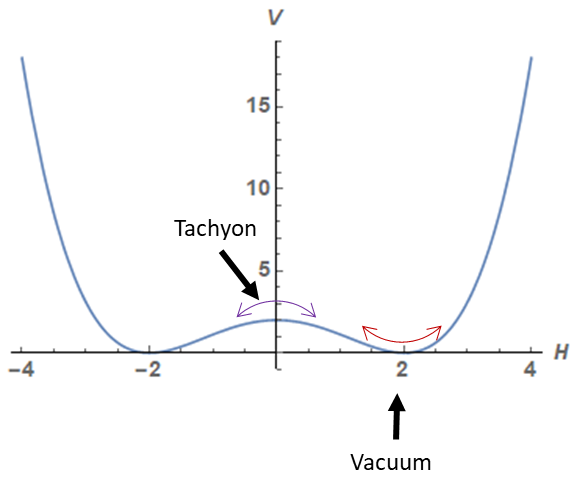
In fact we will never find, in a real vacuum of a quantum field theory, a tachyon; a tachyon is simply a sign that we have chosen a state in which all variation of V with the fields is zero, but which is not a [local] minimum, and therefore not a vacuum.
By the way, the broken phase has another possible vacuum in which < H > = -μH /λ1/2. The logic in that vacuum is exactly the same as in the one I just considered, so all the conclusions are the same too.
The Anderson/Higgs/Brout-Englert Mass-Generation Mechanism
Now what would happen if we had fields H and W and a potential
- V = + ½ mH2 H2 + ¼ λ H4 + ½ mW2 W2 + ⅛ g2 H2 W2
or
- V = – ½ μH2 H2 + ¼ λ H4 + ½ mW2 W2 + ⅛ g2 H2 W2
The first case is the unbroken phase; it would have <H> = 0. Also, <W> = 0, and the coefficient of W2 is mW2, meaning the W particle has mass mW.
- Mass of h particle = mH
- Mass of W particle = mW
But in the second case, we are in the broken phase, < H > = v = μH /λ1/2. Again <W> = 0. Shifting H and writing H = v + h, we find
- V = constant + μH2 h2 + λvh3 + ¼ λh4 + ½ mW2 W2 + ⅛ g2 v2 W2 + ¼ g2 v h W2
We can collect the purely W2 terms
- V = constant + μH2 h2 + λvh3 + ¼ λh4 + ½ (mW2 + ¼ g2 v2) W2 + ¼ g2 v h W2
Now the W field’s mass – the terms multiplying W2 – has shifted
- Mass of h particle = √2 μH
- Mass of W particle = (mW2 + ¼ g2 v2)1/2
In short, a non-zero vev for H (i.e. <H>, or in other words, v) shifts the mass of the W.
And in fact, if mW were zero, then in the unbroken phase the W would have zero rest mass, while in the broken phase its mass would be ½ g v. In short, this is an example in which a massless particle has developed a mass. This is a crude cartoon, but it captures much of the essence of the Anderson/Higgs/Brout-Englert mechanism for mass generation.
To understand why certain mass parameters, such as mW here, must be zero for some fields, and why the corresponding particles therefore require this mechanism in order for them to have any mass at all, requires a longer discussion. We will get back to that later.


25 Responses
Thanks for the technical glimpse into mass mechanisms! I have been lured here because of your publication of “Waves …” and with a little time on my hand found myself unexpectedly looking into “The Anderson/Higgs/Brout-Englert Mass-Generation Mechanism”.
So some nitpicks that tripped me up:
1. Pavel’s note on “variation of V with F” that should be T is still there.
2. On “Then V = – ½ μH^2 (v+h)^2 + ¼ λ (v+h)^4 = – ¼ μH^2 v^2 + μH2 h^2 + λvh^3 + ¼ λh^4
Remember this is the same potential as before, simply rewritten in terms of h instead of H!
In this new form, the first term is a constant and plays no role in determining the vacuum. The term proportional to h vanishes exactly, so =0 is indeed the vacuum.”
2.1 Unless I’m mistaken the – ¼ μH^2 term should be = – 1/2 μH^2. (It isn’t used, of course.)
2.2 Perhaps the “term(s) proportional to h vanishes” is clearer, since there seem to be a lot of unspoken cancellations here.
Test failed, the comment system removes automatically anything that is between > and H < (operator?) is.
Not sure what to do about that; maybe if you use a slash before the greater than sign? Note also that v_H is another way to write “vev of H” and maybe you’ll have to use that in comments.
This is just a test, maybe this form prints, using > and < as brackets in a comment has some unexpected consequences:
And also, please explain what and vev is,
End of test
“vev” stands for Vacuum Expectation Value. It was defined on the first page, https://profmattstrassler.com/technical-zone/the-triplet-the-w-mass/1-the-vacuum-of-field-theory/ , but I should have reiterated it here.
Very interesting and illuminating so far, as it allows a deep view into how a theoretical physicist thinks. Since I am not sufficiently knowledgeable about either quantum physics or relativity, I cannot comment upon the validity of what Prof. Strassler has written. But as I am knowledgeable about thermodynamics and chemistry, I can comment about what has been left out so far, and what I hope will be addressed in a future post. And what has been left out so far makes that what has been written bogus. Period.
Why? Because the mathematics presented are based upon equilibrium thermodynamics, i.e. firstly the assumption that enough time has passed that the minimum of the potential has been reached, and secondly that particle size considerations and quantum fluctuations do not prohibit reaching minimum. The latter means that, so far as it has been presented, Prof Strassler’s derivation presumes that the uncertainty principle is not applicable.
Let me illustrate my – general – statements with a few examples. We are all familiar with what happens when mixing hydrogen gas with oxygen gas at room temperature: Nothing, it is just a mixture of two gases, and no more. But add a spark to it, or a little bit of platinum sponge, or heat it a few hundred degrees, and – boom – the hydrogen reacts with the oxygen and forms H2O (water, in the form of steam). If I had been sufficiently patient and waited a few million years, my hydrogen/oxygen mixture would have turned into water at room temperature as well, for the same reason that adding a catalyst (platinum), or a spark, or thermal energy (heat): hydrogen and oxygen atoms need to fly into one another at a sufficiently high velocity to overcome the repulsion originating in their hull electrons all having the same charge. What needs to be considered here is the probability with which the repulsion is overcome by the momentum exchanged in any individual collision.
The same argument, with different names, holds for quantum physics as well. On a large scale, our sun is still fusing hydrogen into helium, releasing energy. If equilibrium thermodynamics were to apply, the sun would not be radiating any energy at all, having burned all its hydrogen, transformed into a white dwarf, radiated all its heat and eventually fused with all the other matter in the universe into a single black hole. This has not happened – yet?
On a smaller scale, the W boson does decay into other particles, indicating again that it is itself not in the minimum of potential energy that is possible to achieve – which is a single universe-wide black hole, without any quarrelsome human in it.
In chemistry, the probability of a reaction to occur is ultimately determined by the probability that two molecules (and all molecules are particles) collide. Chemists learn to manipulate this probability using catalysts, temperature, and, particularly in Organic Chemistry, by manipulating the shape of the electron cloud surrounding a particle. In quantum physics the probability of an event is determined, at least to the best of my knowledge, by Werner Heisenberg’s uncertainty principle, which arises from particles being “ripples in a field”, and thus that the smallest observable distance is determined by the size of that ripple. This may not be true, and the uncertainty principle may need to be revised: compare https://en.wikipedia.org/wiki/Super-resolution_imaging and https://en.wikipedia.org/wiki/Uncertainty_principle. (As often, the math here is out of my reach, but I am trying to learn)
To come back to the beginning of a long and circuitous argument, figure 4 in the first post shows a nice representation of the phase transformation gas -> liquid, i.e. a mathematical representation of the critical point. But it leaves out entirely what happens during the transformation, when liquid droplets are created: The volume occupied by the liquid phase contains less energy EsubLiquid than the gas phase, i.e.
EsubLiquid = – a times DropletRadius cubed
but to get there, a new surface has to be formed that previously did not exist:
EsubSurface = + b times DropletRadius squared
thus in toto the energy released during phase transformation is
EsubTransformation = EsubSurface – EsubLiquid = b times DropletRadius squared – a times DropletRadius cubed
(a and b are taken as constants here, describing volume and surface energy respectively. Both are positive scalars)
Since a particle will occupy a volume, it also must have a surface. Thus, what I have presented here must hold for any quantum particle as well, and not just for the gas -> liquid transition. It also means that a particle is located, in the framework given by figure 3 of the first post, on the graph, in the boundaries given by
0 >= V >= -1 and 2 >= T >= -2
It also means that, in the framework of the only figure of this post, particles will have complex mass and can travel at velocities both smaller and larger than the velocity of light, as they exist somewhere on the curve between
0 <= V <=2 and -2 <= T <= 2
and not on either minimum of the potential.
And lastly: please explain what a potential density is. I have taken potential here to mean potential energy as a function of some coordinates (x,y,z,t), and have no idea what to divide it by to obtain a density. And also, please explain what and vev is, since that (operator?) never appeared anywhere in my math training.
Density: literally, energy per unit volume as a function of position (x,y,z) and time (t). Nothing more.
Regarding uncertainty and thermodynamics: these are fair questions. There’s a lot of dissipation going on that would require further discussion. You are correct that as the universe cools, thermal fluctuations in the H and W fields are large, but they dissipate because the H and W particles (i.e. ripples in those fields) decay; this helps these fields find their minima very rapidly, on microscopic time scales, once the temperature is low enough that the H and W particles can’t be produced by thermal effects (k_B T < m c^2 ). In the end all the unstable particles of the Standard Model decay into more stable ones, and the fields for those particles reach their minima. What remains is the photon and neutrino radiation from the heat of the early universe, along with a small number of stable particles (electrons, protons, neutrons, and a few of their anti-particles, which are for some reason rare.)
Quantum fluctuations of the fields around their minima are not relevant for this story, but yes, that requires a long discussion too. What we mean by "the potential" has to be unpacked; what I'm really using here, though it's not obvious at all, is a quantum-corrected version of the potential, so many of these effects have implicitly begin accounted for already. But that gets us into the concept of "renormalization" (i.e. accounting properly for the shifts caused by quantum effects *before* you start calculating) and this is a long story that is not illuminating for my current purposes.
[(time variation of F)2 – c2(space variation of F)2] = – [c4 / ħ2] the variation of V with F
If I understand it well, there shall be T instead of F.
As in the first webpage, I meant “F” to be a general field. But I should have said so, or used T. Will fix that.
Prof. Strassler:
Is it true that the only energy in a quantum field above the vacuum energy coms from ripples and disturbances? Ripples are your name for the quanta of the field while disturbances are your non-confusing name for the conventional name of virtual particles. It seems ripple is one of those brilliant approximations like point mass, rigid body and ideal gas.
Since all quantum fields are subject to the Uncertainty Principle they undergo vacuum fluctuations. I presume these vacuum fluctuations are disturbances. So every quantum field contains disturbances but may or may not contain ripples. For a quantum field to contain ripples must there be either a source function for the field, interactions with other quantum fields or both.
Would the circular waves created by rain drops falling on a small otherwise still pond be a good analog for the free particles in a two dimension non-interacting quantum field? Would the chop in the ocean be a good analog for a disturbance in a quantum field?
Many thanks for your efforts to bring an understanding of quantum field theory to the non-professionals.
The best way to say it is that a ripple is a solution to an equation of motion like the one written above, where only F appears, whereas a generalized disturbance need not be a solution to that equation. In math language, a ripple satisfies a homogeneous equation, whereas a generalized disturbance need not satisfy that equation (though it may, in some contexts, satisfy an inhomogeneous equation which has a source of some sort, where that source might indeed be other fields.) But this is a long, long story. I can’t teach all of this at the same time, I’m afraid. Perhaps I’ll come back to your question at some point in another context.
“Would the circular waves created by rain drops falling on a small otherwise still pond be a good analog for the free particles in a two dimension non-interacting quantum field? ” Not a bad analogue, but not the full story either. “Particle” is a misnomer: a particle is a quantum of a wave. So a circular ripple would be an analog for a free “particle” in a superposition of states with different directions of motion, or alternatively, for a large collection of free particles each moving in different directions. A “plane wave” is a simpler analogue in many cases, in that it better represents what we intuitively think of as a “particle”, namely something with a definite momentum.
“Would the chop in the ocean be a good analog for a disturbance in a quantum field?” Neither yes nor no, I think. It at least moves your mind away from simple ripples, so that’s good. But context matters; it won’t always be helpful. Moreover, things can happen in quantum physics (especially superposition) which have no classical-physics analogue. So any such image will be useful in some ways and incomplete in others. (The best way to learn how this works is to see how the math and physics work together in examples… which I haven’t really attempted to show up to now.)
Little nitpicking! “p is the particle’s momentum (and the speed of the particle is pc/E)”
pc/E is v/c.
Ooops! thanks…
In the formula
(E2 – p2c2)/ ħ2 f(x,t) = mT2 [c4 / ħ2] f(x,t) + λ [c4 / ħ2] f(x,t)3
there shall be mH (or I misunderstood it)
Thanks for catching that — fixed!
Very interesting as usual.
In the H cube case you mentioned interestingly: « is that our ripple may or may not live forever, but it will still live for a long enough time to be meaningfully described as a particle ». Could that be interpreted as a virtual particle?
Thank you.
No, there’s still an honest-to-goodness particle here, as long as the cubic term is small enough. But to explain this properly, and be really precise about what a “particle” is, we would have to account for quantum physics and consider the full context of the theory; the mathematics required suddenly jumps from pre-university to post-university. That’s why I pushed this issue under the rug.
So can we safely assume (as a layman) that when you use the word “particle” you don’t mean a sphere with finite radius, like the first image here https://scitechdaily.com/subatomic-particle-disintegration-violates-the-standard-model-of-physics-completely-unexpected/
Elementary “particles” are certainly not correctly depicted as spheres with finite radius. In the picture you cited, the quarks and anti-quarks are drawn as vastly too large, and their wave-like properties are not indicated. The quarks are much more like the photons than the picture would suggest.
That said, composite particles like the Kaon and pion, like protons and neutrons, *do* have a size. To depict them is even more difficult, because they do have a radius and yet retain some wave-like properties. Moreover, they are far more complex than drawn in the picture. So there’s not really a way to draw them without leaving some qualities out.
«A particle is simply a tiny ripple in a field.»
This confuses me. Why are you calling a ripple “particle”? Why not call a ripple a ripple? And what is the mass of a ripple? Is it its frequency?
The ripple’s amplitude is quantized (it can only have particular values) and the smallest value corresponds to a single particle. If you want more details I suggest you read through https://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/
Frequency is related to *energy*. But if the particle is stationary (p=0), then frequency is proportional to rest mass, because of the relationship (for a stationary particle) between E and m.
Momentum ‘p’ varies with the Mass Parameters never is Zero. Only if Mass factor lose inside the Vacuum as a Model (standard), ‘p’ is Zero and ‘Reast’mass’ replace it in mathematics?
/The same potential as before, simply NOT rewritten in terms of h instead of H!/?
In one of the vacua of the broken phase, H is NOT = + a cos([E t – p x] / ħ) = μH /λ1/2 + a cos([E t – p x] / ħ)
so that it is a ripple around the actual vacuum, where the field is constant, uniform and non-zero.
….instead the connecting (the correlation which appears like tachyon) is replaced by “Rest-mass “, the imaginary ‘matter waves” by Paul Dirac was rather to understand the Machine than Machine understand Humans.
In the broken phase, the “Local Maximum (connection) in the vacuum is there, at HighEnergy, so all the conclusions are the same too?
Holography is represented by Electron. Radio-active decay (ground state or localization) is electromagnetic radiation. Opposite to this (local maximum) is “Mass creation”. ?
Just spotted: “Similarly, p/ħ, which multiplies x, determines the time dependence of the ripple”. Probably space dependence shell be there.
Fixed – thanks!