It’s been quite a while (for good reason, as you’ll see) since I gave you a status update on the search for supersymmetry, one of several speculative ideas for what might lie beyond the known particles and forces. Specifically, supersymmetry is one option (the most popular and most reviled, perhaps, but hardly the only one) for what might resolve the so-called “naturalness” puzzle, closely related to the “hierarchy problem” — Why is gravity so vastly weaker than the other forces? Why is the Higgs particle‘s mass so small compared to the mass of the lightest possible black hole?
POSTED BY Matt Strassler
ON December 11, 2013
[Note: If you missed Wednesday evening’s discussion of particle physics involving me, Sean Carroll and Alan Boyle, you can listen to it here.]
I still have a lot of work to do before I can myself write intelligently about the Fukushima Daiichi nuclear plant, and the nuclear accident and cleanup that occurred there. (See here and here for a couple of previous posts about it.) But I did want to draw your attention to one of the better newspaper articles that I’ve seen written about it, by Ian Sample at the Guardian. I can’t vouch for everything that Sample says, but given what I’ve read and investigated myself, I think he finds the right balance. He’s neither scaring people unnecessarily, nor reassuring them that everything will surely be just fine and that there’s no reason to be worried about anything. From what I know and understand, the situation is more or less just as serious and worthy of concern as Sample says it is; but conversely, I don’t have any reason to think it is much worse than what he describes.
Meanwhile, just as I don’t particularly trust anything said by TEPCO, the apparently incompetent and corrupt Japanese power company that runs and is trying to clean up the Fukushima plant, I’m also continuing to see lots of scary articles — totally irresponsible — written by people who should know better but seem bent upon frightening the public. The more wild the misstatements and misleading statements, the better, it seems.
One example of this kind of fear-mongering is to be found here: http://truth-out.org/news/item/19547-fukushima-a-global-threat-that-requires-a-global-response, by Kevin Zeese and Margaret Flowers. It’s one piece of junk after the next: the strategy is to take a fact, take another unrelated fact, quote a non-expert (or quote an expert out of context), stick them all together, and wow! frightening!! But here’s the thing: An experienced and attentive reader will know, after a few paragraphs, to ignore this article. Why?
Because it never puts anything in context. “When contact with radioactive cesium occurs, which is highly unlikely, a person can experience cell damage due to radiation of the cesium particles. Due to this, effects such as nausea, vomiting, diarrhea and bleeding may occur. When the exposure lasts a long time, people may even lose consciousness. Coma or even death may then follow. How serious the effects are depends upon the resistance of individual persons and the duration of exposure and the concentration a person is exposed to, experts say.” Well, how much cesium are we talking about here? Lots or a little? Ah, they don’t tell you that. [The answer: enormous amounts. There’s no chance of you getting anywhere near that amount of exposure unless you yourself go wandering around on the Fukushima grounds, and go some place you’re really not supposed to go. This didn’t even happened to the workers who were at the Fukushima plant when everything was at its worst in March 2011. Even if you ate a fish every week from just off Japan that had a small amount of cesium in it, this would not happen to you.]
Because it makes illogical statements. “Since the accident at Fukushima on March 11, 2011, three reactor cores have gone missing.” Really? Gone missing? Does that make sense? Well then, why is so much radioactive cooling water — which is mentioned later in the article — being stored up at the Fukushima site? Isn’t that water being used to keep those cores cool? And how could that happen if the cores were missing? [The cores melted; it’s not known precisely what shape they are in or precisely how much of each is inside or outside the original containment vessel, but they’re being successfully cooled by water, so it’s clear roughly where they are. They’re not “missing”; that’s a wild over-statement.]
Because the authors quote people without being careful to explain clearly who they are. “Harvey Wasserman, who has been working on nuclear energy issues for over 40 years,…” Is Harvey Wasserman a scientist or engineer? No. But he gets lots of press in this article (and elsewhere.) [Wikipedia says: “Harvey Franklin Wasserman (born December 31, 1945) is an American journalist, author, democracy activist, and advocate for renewable energy. He has been a strategist and organizer in the anti-nuclear movement in the United States for over 30 years.” I have nothing against Mr. Wasserman and I personally support both renewable energy and the elimination of nuclear power. But as far as I know, Wasserman has no scientific training, and is not an expert on cleaning up a nuclear plant and the risks thereof… and he’s an anti-nuclear activist, so you do have to worry he’s going to make thing sound worse than they are. Always look up the people being quoted!]
Because the article never once provides balance or nuance: absolutely everything is awful, awful, awful. I’m sorry, but things are never that black and white, or rather, black and black. There are shades of gray in the real world, and it’s important to tease them out a little bit. There are eventualities that would be really terrible, others that would be unfortunate, still others that would merely be a little disruptive in the local area — and they’re not equally bad, nor are they equally likely. [I don’t get any sense that the authors are trying to help their readers understand; they’re just bashing the reader over the head with one terrifying-sounding thing after another. This kind of article just isn’t credible.]
The lesson: one has to be a critical, careful reader, and read between the lines! In contrast to Sample’s article in the Guardian, the document by Zeese and Flowers is not intended to inform; it is intended to frighten, period. I urge you to avoid getting your information from sources like that one. Find reliable, sensible people — Ian Sample is in that category, I think — and stick with them. And I would ignore anything Zeese and Flowers have to say in the future; people who’d write an article like theirs have no credibility.
POSTED BY Matt Strassler
ON December 9, 2013
I’m sure you’ve all read in books that Venus is a planet that orbits the Sun and is closer to the Sun than is the Earth. But why learn from books what you can check for yourself?!?
[Note: If you missed Wednesday evening’s discussion of particle physics involving me, Sean Carroll and Alan Boyle, you can listen to it here.]
As many feared, Comet ISON didn’t survive its close visit to the Sun, so there’s no reason to get up at 6 in the morning to go looking for it. [You might want to look for dim but pretty Comet Lovejoy, however, barely visible to the naked eye from dark skies.] At 6 in the evening, however, there’s good reason to be looking in the western skies — the Moon (for the next few days) and Venus (for the next few weeks) are shining brightly there. Right now Venus is about as bright as it ever gets during its cycle.
The very best way to look at them is with binoculars, or a small telescope. Easily with the telescope, and less easily with binoculars (you’ll need steady hands and sharp eyes, so be patient) you should be able to see that it’s not just the Moon that forms a crescent right now: Venus does too!
If you watch Venus in your binoculars or telescope over the next few weeks, you’ll see proof, with your own eyes, that Venus, like the Earth, orbits the Sun, and it does so at a distance smaller than the distance from the Sun to Earth.
The proof is simple enough, and Galileo himself provided it, by pointing his rudimentary telescope at the Sun 400 years ago, and watching Venus carefully, week by week. What he saw was this: that when Venus was in the evening sky (every few months it moves from the evening sky to the morning sky, and then back again; it’s never in both),
- it was first rather dim, low in the sky at sunset, and nearly a disk, though a rather small one;
- then it would grow bright, larger, high in the sky at sunset, and develop a half-moon and then a crescent shape;
- and finally it would drop lower in the sky again at sunset, still rather bright, but now a thin crescent that was even larger from tip to tip than before.
The reason for this is illustrated in the figure below, taken from this post [which, although specific in some ways to the sky in February 2012, still has a number of general observations about the skies that apply at any time.]
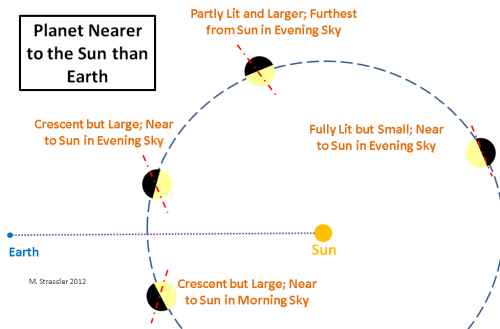
So go dig out those binoculars and telescopes, or use Venus as an excuse to buy new ones! Watch Venus, week by week, as it grows larger in the sky and becomes a thinner crescent, moving ever closer to the sunset horizon. And a month from now the Moon, having made its orbit round the Earth, will return as a new crescent for you to admire.
Of course there’s another proof that Venus is closer to the Sun than Earth is: on very rare occasions Venus passes directly between the Earth and the Sun. No more of those “transits” for a long time I’m afraid, but you can see pictures of last June’s transit here, and read about the great scientific value of such transits here.
POSTED BY Matt Strassler
ON December 6, 2013
Today, Wednesday December 4th, at 8 pm Eastern/5 pm Pacific time, Sean Carroll and I will be interviewed again by Alan Boyle on “Virtually Speaking Science”. The link where you can listen in (in real time or at your leisure) is
What is “Virtually Speaking Science“? It is an online radio program that presents, according to its website:
- Informal conversations hosted by science writers Alan Boyle, Tom Levenson and Jennifer Ouellette, who explore the explore the often-volatile landscape of science, politics and policy, the history and economics of science, science deniers and its relationship to democracy, and the role of women in the sciences.
Sean Carroll is a Caltech physicist, astrophysicist, writer and speaker, blogger at Preposterous Universe, who recently completed an excellent and now prize-winning popular book (which I highly recommend) on the Higgs particle, entitled “The Particle at the End of the Universe“. Our interviewer Alan Boyle is a noted science writer, author of the book “The Case for Pluto“, winner of many awards, and currently NBC News Digital’s science editor [at the blog “Cosmic Log“].
Sean and I were interviewed in February by Alan on this program; here’s the link. I was interviewed on Virtually Speaking Science once before, by Tom Levenson, about the Large Hadron Collider (here’s the link). Also, my public talk “The Quest for the Higgs Particle” is posted in their website (here’s the link to the audio and to the slides).
POSTED BY Matt Strassler
ON December 4, 2013
Ah, the fast-paced life of a theoretical physicist! I just got done giving a one-hour talk in Rome, given at a workshop for experts on the ATLAS experiment, one of the two general purpose experiments at the Large Hadron Collider [LHC]. Tomorrow morning I’ll be talking with a colleague at the Rutherford Appleton Lab in the U.K., an expert from CMS (the other general purpose experiment at the LHC). Then it’s off to San Francisco, where tomorrow (Wednesday, 5 p.m. Pacific Time, 8 p.m. Eastern), at the Exploratorium, I’ll be joined by Caltech’s Sean Carroll, who is an expert on cosmology and particle physics and whose book on the Higgs boson discovery just won a nice prize, and we’ll be discussing science with science writer Alan Boyle, as we did back in February. [You can click here to listen in to Wednesday’s event.] Next, on Thursday I’ll be at a meeting hosted in Stony Brook, on Long Island in New York State, discussing a Higgs-particle-related scientific project with theoretical physics colleagues as far flung as Hong Kong. On Friday I shall rest.
“How does he do it?”, you ask. Hey, a private jet is a wonderful thing! Simple, convenient, no waiting at the gate; I highly recommend it! However — I don’t own one. All I have is Skype, and other Skype-like software. My words will cross the globe, but my body won’t be going anywhere this week.
We should not take this kind of communication for granted! If the speed of light were 186,000 miles (300,000 kilometers) per hour, instead of 186,000 miles (300,000 kilometers) per second, ordinary life wouldn’t obviously change that much, but we simply couldn’t communicate internationally the way we do. It’s 4100 miles (6500 kilometers) across the earth’s surface to Rome; light takes about 0.02 seconds to travel that distance, so that’s the fastest anything can travel to make the trip. But if light traveled 186,000 miles per hour, then it would take over a minute for my words to reach Rome, making conversation completely impossible. A back-and-forth conversation would be difficult even between New York and Boston — for any signal to travel the 200 miles (300 kilometers) would require four seconds, so you’d be waiting for 8 seconds to hear the other person answer your questions. We’d have similar problems — slightly less severe — if the earth were as large as the sun. And someday, as we populate the solar system, we’ll actually have this problem.
So think about that next time you call or Skype or otherwise contact a distant friend or colleague, and you have a conversation just as though you were next door, despite your being separated half-way round the planet. It’s a small world (and a fast one) after all.
POSTED BY Matt Strassler
ON December 3, 2013
Take a ball of loosely aggregated rock and ice, the nucleus of a comet, fresh from the distant reaches of the solar system. Throw it past the sun, really fast, but so close that the sun takes up a large fraction of the sky. What’s going to happen? The answer: nobody knows for sure. Yesterday we actually got to see this experiment carried out by nature. And what happened? After all the photographs and other data, nobody knows for sure. Comet ISON dimmed sharply and virtually disappeared, then, in part, reappeared [see the SOHO satellite’s latest photo below, showing a medium-bright comet-like smudge receding from the sun, which is blacked out to protect the camera.] What is its future, and how bright will it be in the sky when it starts to be potentially visible at dawn in a day or two? Nobody knows for sure.
[Note Added — Now we know: the comet did not survive, and the bright spot that appeared shortly after closest approach to the sun appears to have been all debris, without a cometary “core”, or nucleus, to produce the additional dust and gas to maintain the comet’s appearance. Farewell, ISON! Click here to see the video of the comet’s pass by the sun, its brief flare after passage, and the ensuing fade-out.]
I could not possibly express this better than was done last night in a terrific post by Karl Battams, who has been blogging for NASA’s Comet ISON Observing Campaign. He playfully calls ISON “Schroedinger’s Comet”, in honor of Schroedinger’s Cat, referring to a famous and conceptually puzzling thought-experiment of Erwin Schroedinger, in which a cat is (in a sense) put in a quantum state in which it is neither/both alive nor/and dead. Linking the comet and the cat is a matter of poetic metaphor, not scientific analogy, but the metaphor is a pretty one.
Battams’ post beautifully captures the slightly giddy mindset of a scientist in the midst of intellectual chaos, one whose ideas, expectations and understanding are currently strewn about the solar system. He brings to you the experience of being flooded with data and being humbled by it… a moment simultaneously exciting and frustrating, when scientists know they’re about to learn something important, but right now they haven’t the faintest idea what going on.
POSTED BY Matt Strassler
ON November 29, 2013
Buy The Book
Reading My Book?
Got a question? Ask it here.
Media Inquiries
For media inquiries, click here.

