Matt Strassler [20 Jan 2012]
In the previous article in this series, I explained why a type of particle that can travel in an extra dimension will seem, to naive observers who do not know about the extra dimension, to have Kaluza-Klein (KK) partners — heavy versions of the original type of particle. What I pointed out to you was that when the original particle (with mass m) moves in the direction of an extra dimension, it appears to a naive observer to be stationary and heavier than it should be, as though it is another type of particle. This class of apparently new particles, similar to the original one but heavier, are called KK partners.
In the case of a strip, if a particle of mass m is moving across the strip with momentum pacross, an observer who believes the strip is a line will think the particle is a KK partner with zero momentum and mass M, where
M2 = m2 + (pacross /c)2 > m2 .
Though largely correct, this argument seemed to imply that there should be one KK partner for each and every mass M that is larger than m. But that’s not the case… because our world is a quantum world. (See Figure 1 of the previous article.) Let’s now learn why quantum mechanics changes this picture.
The key feature of quantum physics that we need is this: for a quantum “particle” traveling in a dimension of finite length, not all possible values of pacross are allowed. Stated more generally: quantum mechanics tells us that a “particle” that is moving in a dimension that is finite in length can only have certain particular values of momentum in that direction.
This is one of the most important and odd consequences of quantum mechanics! At first glance it is very counterintuitive, because what could stop you from giving a particle that has momentum p a tiny little push, so that it has just a tiny little bit more momentum than p ?
What is a “quantum”?
You may have already noted that I have started putting quotation marks around the word particle, because in the current context I need to distinguish the term“particle,” as used to describe electrons, photons, muons, quarks, gluons, and all the rest of the known elementary “particles”, from the intuitive notion of particle that we inherit from our experience of dust, sand, salt, and grit. Electrons and photons are not like little specks of dust, or grains of sand. In fact, it is better to call a “particle” such as an electron, photon, quark, etc. a “quantum”, which is a more subtle object. These “quanta” [plural of quantum, as memoranda is plural of memorandum] are ripples in fields, more like waves than particles in many respects. In fact, the best way to understand a quantum is to first think about waves. [Another crucial linguistic point: when I say, “wave”, I don’t mean something like a single ocean wave that breaks once on the beach — I really mean a “wave train”, with many crests and many troughs.]
An example of such waves would be electromagnetic waves, among which are the light waves that our eyes can detect. Now imagine taking such a wave — say, the light from a laser — and dimming the light, further and further. How dim can you go? It turns out that in our quantum world, there is a dimmest possible flash of light, which we call a “quantum” of light, or a “photon”. A photon is the light wave whose wave-height, and whose intensity, is the smallest possible. [These concepts and names are due to Einstein, who — despite his reputation for having been unhappy with the conceptual implications of quantum mechanics — was one of the founders of the theory. Caution: like most words, quantum can have multiple meanings, though you won’t see any of the others in this article.]
There’s nothing intuitive — at least nothing that I personally find intuitive — about the fact that light waves are made from quanta, because no process of which we are consciously aware exhibits this effect. But our bodies, through processes of which we are not aware, use this fact all the time. In fact, though light from a light bulb looks continuous to our brains, our eyes are actually absorbing photons one at a time. Moreover, I’ve seen, with my own eyes, clear evidence that light is made from quanta; it’s not something I know just from books. I’ll explain that some other time.
We physicists often call this quantum of light a “particle of light” because in many respects it does behave like a particle. Any given photon that is traveling in a straight line on its own has a definite energy and momentum; all photons have the same mass (in particular, zero); a photon cannot be divided into smaller pieces; and a photon can be emitted or absorbed only as a whole. These properties roughly (though imperfectly) correspond to what our intuition would expect of particles, such as grains of sand, marbles, dust specks, etc.
But the word “quantum” is in many ways a better word than “particle”, because some of the properties of a quantum are similar to those of particles and some are similar to those of waves. A well-known example of wave-like behavior is that a quantum can pass through two doors simultaneously, and can interfere (in the same sense that waves can interfere, where a wave crest and wave trough can cancel each other out) with itself. And we’re about to see another example.
You should keep in mind that what is true for the photon is true for all the known “particles”. Really, each one is a type of quantum — a wave of smallest possible height in a corresponding field. The electron is a quantum in the electron field. An up quark is a quantum in the up quark field. The Z particle is a quantum of the Z field… and so on.
Kaluza-Klein Partner Quanta
Now it’s time to learn what I’ve been promising to explain to you: why the wavelike nature of quanta implies that the masses of Kaluza-Klein partners take certain specific values, rather than all possible values larger than the mass m of the original “particle.” The famous physicist Louis de Broglie (following initial insights of Einstein) was the first to state clearly that the relation between waves, particles and quanta implies that for a quantum there is a relation between
- its momentum (a particle-like property) and
- its wavelength (a wave-like property) [where again you must read the word “wave” as “wave-train”, not as a single wave at the beach — and the wavelength is the distance between crests of the wave-train]
and this relation is simply: momentum = h / wavelength .

Here h is Max Planck’s famous constant, as fundamental a constant of nature as is the speed of light. Planck introduced this constant in 1900 while trying to resolve a puzzling physical phenomenon that I’ll explain elsewhere; it was the first step toward our quantum picture of the world. Wherever you try to describe a phenomenon in which quantum mechanics plays an important role, h will appear. [In many formulas you see the quantity ℏ, which is just h divided by 2π , because often that quantity is more convenient for keeping formulas simple.]
Now in some ways it turns out to be a little simpler to explain what happens for a quantum traveling on a tube, rather than on the strip that we’ve used in all the previous examples. [I discussed the strip and the tube together in the context of Worlds of 2 Spatial Dimensions.] Almost everything I’ll say for the tube turns out to be true on the strip too. For this reason I’ll explain both of them together.
The Lightest KK Partner

Let’s think about a quantum traveling on the strip (of width W) or tube (of circumference S). First, imagine a quantum traveling in the long dimension [long meaning infinite, or so long that it might as well be infinite as far as any of us can tell.] A wave traveling along the strip or tube can move along the long dimension in either direction, and can have any wavelength (the distance between its wave crests). See Figure 2. Such a quantum can therefore have any momentum along the strip or tube, according to de Broglie: the momentum can be zero, very small, small, large, in either direction, etc. In principle you can make the momentum a little bigger (or a little smaller) by pushing on the quantum in the direction (or opposite the direction) of its motion.

But now consider a quantum (i.e. “particle”) traveling across the strip or tube. First of all, it clearly cannot have a wavelength that is longer than the distance across the strip or around the tube! This is easy to see on the tube: there has to be at least one crest and at least one trough somewhere around the tube, moving around the tube, as shown in Figure 3. If the wavelength is larger than S, the wave will not connect smoothly back on itself, as shown in Figure 4 (left). The largest wavelength the wave can have is exactly S; the one and only trough in the wave must be on exactly the opposite side of the tube from the one and only crest.

The crest and trough of the wave in Figure 3 move around and around the tube, somewhat analogous (see Figure 5) to an ordinary non-quantum particle (here I really do mean something like a grain of sand, not a quantum or “particle”) running around the tube, but crucially different: while the ordinary intuitive particle could without a problem go slightly slower or slightly faster, giving it a slightly larger or smaller momentum, the quantum corresponding to the wave cannot have a slightly larger or slightly smaller momentum, because that would correspond to an unacceptable wavelength, such as in Figure 4.

On the strip it is a little trickier, but as shown in Figure 6 it turns out that there has to again be one crest at one wall and one trough at the other, which change over time as shown in the figure: the crest doesn’t move, but it decreases in size and then turns into a trough, while the trough turns into a crest. [Note that unlike Figure 3, where the crest and trough stay the same size but move around the tube, the crest of this wave doesn’t move as it shrinks. This is therefore called a “standing wave”. Think of a wave on a guitar string or a violin string for a similar (but not identical) example. ] Intuitively this standing wave corresponds to an ordinary non-quantum particle going back and forth across the strip. (Less intuitively, but more accurately, it corresponds to an ordinary particle doing both at the same time. But that rather strange and cool quantum fact is not essential right now.) This is indicated in Figure 7.

In both cases there is a largest possible wavelength (S for the tube, 2 W for the strip). And that means there is a smallest possible momentum (h/S and h/ 2 W for the tube and strip). And finally, that means there is a lightest-possible Kaluza-Klein particle! which has mass M, where
- M2 = m2 + (pacross / c)2 = m2 + (h / c S)2 (tube)
- M2 = m2 + (pacross / c)2 = m2 + (h / 2 c W)2 (strip)
Notice for a massless particle (m=0) the formulas simplify to
- M = h / c S (tube)
- M = h / 2 c W (strip)
and these last formulas are approximately right if S or W is also very small, as will often be the case in plausible speculations.

So now we have learned that because “particles” are really quanta, with some wave-like properties,
- the lightest KK partner has a mass M which is quite a bit larger than m, and
- since the formulas above for M have 1/W and 1/S in them, the smaller is the extra dimension, the heavier is the lightest KK partner.
- In fact once S and W are so small that M is much larger than m (or if m is zero to start with), then M is approximately proportional to 1/S or 1/W.
Ok!! That’s the main point, so please make sure you understand it before proceeding. There are a few more things to explain though:
- why there are many KK partners, with different masses M, M’, M”, etc. (where by definition M < M’ < M”, etc. )
- why the masses are separated from one another
- why the masses all grow as the extra dimension(s) become smaller
- why the KK partners of different types of particles that all may travel in the same extra dimension(s) will have similar masses, especially for heavier KK partners
- why the KK partner masses tell us directly about the shape, size and number of extra dimensions
The answers follow very quickly from what I’ve already told you.
Beyond the Lightest KK Partner

Next: why are there many KK partners? That is simply because the quantum waves on the strip or tube can have many different wavelengths. In Figures 8, 9 and 10 you can see waves that have 1/2 or 1/3 of the maximum wavelength, corresponding (according to Einstein and to de Broglie) to quanta of double and triple the minimum momentum.

More generally, any wavelength is allowed for which there are n crests and n troughs, where n is any positive integer (1,2,3,4,…), so that the wavelength of the wave is S divided by n (or 2 W divided by n), and the wave fits neatly inside the circle of circumference S or the line of length W. Any other wavelength (see Figure 4) is not allowed. Correspondingly, given the de Broglie relation momentum = h / wavelength, any momentum of the form n h / S (or n h / 2 W) is allowed, and for each value of n we have a KK partner of mass
- M2 = m2 + (pacross /c)2 = m2 + (n h / c S)2 (tube)
- M2 = m2 + (pacross /c)2 = m2 + (n h / 2 c W)2 (strip)
This now answers most of the questions above, at least for the tube and strip:
- there are many KK partners (one for each integer n>0),
- their masses are well separated from one another (since when you change n by 1, the mass M changes by a lot),
- their masses all grow as the extra dimensions shrink (because the last terms in the formulas become larger as W or S become smaller),
- heavy KK partners for different particles with different masses m have similar masses M (because for large enough n, the second terms in the formulas are large compared to m2, making the KK partner masses approximately M = n h / c S for the tube and n h / 2 c W for the strip, almost independent of m.)

Now we need to answer the last question: why does the number, size and shape of the extra dimensions determine the masses of the KK partners — and thus, conversely, why does measuring the masses of many KK partners permit a determination of the properties of the extra dimensions, much the way listening to the sound of a musical instrument can allow one (in principle) to determine its shape, size, and materials?
Take the simplest (and overly simple!) example first. Let’s consider two extra dimensions and re-use our classic ship canal, including (as we did at the end of a recent article giving examples of extra dimensions) the fact that the canal has depth too, so we can think about waves moving around inside it. (The sound you hear in a hallway, or any underwater sound in the ship canal, would involve waves of this type.) The cross-section of the canal (if we slice it at some point along the longest dimension) is just a rectangle, of width W and depth D. Now just as an ordinary non-quantum particle, even if stationary from the point of view of the long dimension, could move along either or both of the extra dimensions (and thus have momentum either in the width or the depth dimension), so a wave will have a wavelength in both extra dimensions. [This simple separation of the wave into what it is doing in the width dimension and what it is doing in the depth dimension is quite special to a rectangular canal, and will not generally occur in other examples.] For instance, as shown in Figure 11, at the top, one allowed wave would have three troughs in the width direction and one in the depth dimension. We can specify how many troughs and crests there are in the width direction by an integer n1 and similarly in the depth dimension by a number n2, and for each n1 and n2 (where one or both is greater than zero) we have KK partners. For a massless (m=0) or nearly massless quantum, its KK partners have masses
- M2 = m2 + (pwidth/c)2 + (pdepth/c)2 = m2 + (n1 h / 2 c W)2 + (n2 h / 2 c D)2
Thus you see that the pattern of masses is different from the case of one extra dimension, and that the pattern can tell us both W and D.

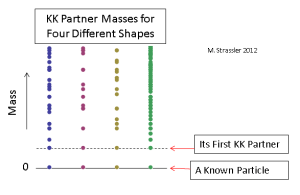
If instead the cross-section of the canal is a different shape — say, a triangle, or a half-disc, as shown in Figure 12 at the bottom, then we will get a different pattern of masses that reflects the precise shape of the triangle or half disc. And we can stop thinking about practical ship canals, and imagine a three-dimensional space whose cross-section is any other finite two-dimensional shape seen in Figure 1 of my article on Worlds of Two Spatial Dimensions: a full disc, or even a sphere or torus. Each of these various shapes will give us a different pattern of KK partner masses. And if the number of extra dimensions is three, or four, or five… vastly more patterns are possible.
Examples of a few patterns, for massless particles, and with the size of the extra dimensions chosen so that the first KK partner mass is the same in each case, are shown in Figure 12. Clearly quite a few KK partner masses must be measured if one is to infer the shape and size of the extra dimensions (or even confirm that any newly discovered heavy particles actually are KK partners) so understanding the nature of any extra dimensions would take time.
Could the Known Heavier Matter Particles be KK Partners of the Lighter Ones?
Now an obvious additional question arises. We know that among the known elementary particles, there is the electron, and there are heavier versions of the electron: the muon and the tau. There is the up quark, and heavier versions of it, the charm and top quarks. There is the down quark, and heavier versions, the strange and the bottom quarks. Are the heavier known particles KK partners of the lighter ones?
It’s tempting at first glance, but the answer is a resounding no. Sorry. It’s not a dumb question by any means. It’s just that it has a smart, negative answer.
The muon and tau, the charm and the top, the strange and the bottom all get their masses from the Higgs field, not from momentum in extra dimensions. This is abundantly clear from detailed experiments. I’ll write more about this later, but as a first hint, read the article on what the world would be like if the Higgs field were zero. Notice that were the Higgs field zero on average, the electron, muon and tau would all be massless [and in fact would be broken up into two types of particles each.] That’s not consistent with the muon and tau being KK partners of the electron.
And there are many other reasons. Perhaps the most serious is that it turns out that since the electron is electrically charged and is surrounded by an electric field, the photon must travel in any dimension that the electron travels in (though the reverse is not true). So if the electron has KK partners, the photon should have KK partners too. But from our formulas (and similar ones that are more general), since the photon is massless and the electron mass (0.0005 GeV/c2) is light compared to the mass of the muon (about 0.1 GeV/c2), if the muon is a KK partner, the photon should have a KK partner of a similar mass. But such a particle, if it existed, would have been discovered decades ago. In fact there are no KK partners for the photon observed in experiments up to masses considerably larger than the Z particle mass… many hundreds of GeV/c2. (The Z particle itself can’t be a photon KK partner; it isn’t similar enough to the photon.) That means that any KK partners of the electron have to be at least that heavy too.
Where do we go next? Experiment.
We’ve gone from theory (the possibility of extra dimensions, and associated math and geometry) to predictions (KK partners.) Next step: what do we know about extra dimensions from experiments? We haven’t seen any KK partners in experiments yet, but we should still ask what we learn from their absence? Quite a lot, actually, as I’ll explain soon… along with a description of how efforts to find signs of extra dimensions continue at the Large Hadron Collider and elsewhere.


46 Responses
thank you for this series, i loved the reading!
one thing bothers me though – maybe i got caught in the representation – but still; can a particle’s angular momentum be considered a movement in an extra dimension? given that any movement in a scale below macro level can be hidden from our (human) perspective.
does it all boil down to scale (which seems to be determined quite arbitrarily here), or is there more to how we intrinsically define extra dimensions?
Hello, with respect to quantizing the wavelength of the KK particles, why does the wave need to be periodic? Why couldn’t it overlap on itself as it does in Fig 4?
Why visitors still use to read news papers when in this technological globe everything is existing
on web?
Today, I went to the beach front with my kids. I found a sea shell and gave it to my 4
year old daughter and said “You can hear the ocean if you put this to your ear.” She placed
the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is
entirely off topic but I had to tell someone!
Absolutely fascinating
I always used to read paragraph in news papers but now as I am a user of net thus from now I am using net for articles or reviews, thanks to web.
Thank you. That’s as good of an explanation as I’ve ever seen, and although it is not completely satisfying, that’s the quantum regime for you: not completely comprehensible intuitively, but it works.
My response was to Matt.
Matt, Thanks.. I have been following these excellent articles and comments on dimensionalities. I am a builder researcher self-employed working in residential construction and am currently doing related research into modular dimensional units as structural geometric arrays of bricks, blocks and panels in application to built environments.
This has been surprisingly chalanging, which is the reason I have read these articles with such interest. It appears that the brick mathematicaly is quite complex, has a ancient history and is perhaps more like an algorithum, because of its three variable dimensions, its physical quantity and it’s ability to produce complex form from self similarity through iterations over time while respecting the limits imposed by applied physics. More importantly it also appears that the geometric stucture and the forces it must contain to stand are somehow interchangeable, perhaps similar to that of the energy mass relation. The math research indicates to me that there are subtle differences as to how our three spatial dimensions interact with each other and with time and gravity.
Can you comment on any research done on dimensional differences or are they treated equally?
Hello Bradley,
While I cannot consider myself a carpenter…..geometrically foundation building is very important?
“This is a practical application to using methods to make square things that will rest above it. So while this might smell of a blend of metaphorical thinking it is truly has an applicability to using what was handed to us for building better those foundations.”
I hope Matt will leave this link ( http://eskesthai.blogspot.com/2006/06/foundational-perspectives.html ) for you
This short paragraph ” ” above can mean many things to different experts…..for you… it may just be about how one could do housebuilding.
Best,
Plato, Thank you,
I read and really appreciated the essay you forwarded to me in response to my earlier post. It was remarkably prescient and touched two aspects that I recognize as familliar clues to my analyses from which I will try to reframe my question.
” We are all familiar with our three known dimensions of space and one of time, (and for the moment I would like to not include time and higher dimensions). A point in space has no physical quantity as a line dimension needs a length and the three space length dimensions together constitute a 3D volume. From this unit cube we can describe a 3D array of any scale as a coordinate grid array of space. An object in this space by the above definition would be an object of three dimensions in a space of the above array of three dimensions.
Very often when we try to understand this mathematically we reduce to two dimensions as a first step, which is a unit grid, to simplify adding the 3D volume later. This is very much how the design process works for a house and when the foundation is laid a height stationary transit level can be employed to facilitate the 2D layout of the house.
The essay described an application of the Pythagorean right angle theorem, the first triplet 3/4/5, a very old method used even today to ensure the correct positioning of the corners to achive a grid square. In all of this prologue lies the question. Does the mathematics of this process limit the results that can be obtained of describing a 3D space from a simplified 2D foundation to which the necessary volume is added, perhaps by layers to achive a 3D form?
At this point, to make things relevant to a discussion of physics I would point out that the algebra which Is used here is the foundation mathematical method Einstien was looking for to add time as a dimension, and was introduced to him by his close friend Bepo’ who came across the works of Bernarnd Riemann, 50 years before Einstien, he proposed the concept of geometry and force being unified which I understand was instrumental to Einstiens theory’s of relativity and gravitation . Further to this again the mathematics of higher dimension are extra terms added to the Pythagorean theory, though more difficult to visualize but relevant also. What I have found interesting about all this is that how we analyze things from a simplified imaginary 2D perspective to try to get an understanding of the vastly more complex real three dimensional space, all of which could limit or complicate the results obtainable.
In the brick analogue this is demonstrably true as in practice it has only two practical and nesesary units needed, a ratio of 1:2 to complete the foundation layer, the third dimension of the brick is more related to the weight of one brick of one scale unit appropriate to handling in the building process and through trial and error was averaged to three brick layered thereby completing a equal unit 3D cube, again a mathematical analogue.
Through a long process mostly spent examining the historical record can I infer now that how we construct a picture of 3D reality is still somehow incomplete and a two dimensional representation of a gravitational field afecting a three dimensional object I find equally unsatisfying. It was only after I seriously started looking at the math did things start to make some sense of what the geometry of a brick would need to be to really work in 3d… But for now, it’s late and I need sleep. I really hope this is a positive contribution to this discussion.
Thanks
Matt,
Here is my very first question:
What is a field exactly? I asked Lawrence Krauss the other day at a presentation and he looked puzzled and said “numbers” (like a matrix of numbers). We know fields exist, like magnetic fields that can be seen via iron filings, but what is the field itself made of? Force carriers like gauge bosons in a matrix?
And are quantum fields some kind of space/time sheets on which ripples occur? People analogize fields as grids or screens where events occur probabilistically, but do we know what the field is constructed of?
Thanks for any answer you may offer.
Well, let’s step back. If we ask, what is X made of, the answer may be: it is made from Y. If we ask what is Y made of, the answer may be: it is made from Z. But at some point, these questions have to stop. Something is the fundamental ingredient from which everything is made.
In modern quantum field theory, fields ARE that ingredient. They aren’t made from anything; everything is made from them, and their ripples (more precisely, their quantized ripples, which we call quanta, or particles.) More precisely: the elementary particles of nature are ripples on the elementary fields of nature, and as far as we know, those fields are just what exists.
Now we don’t know for sure that this is the case. There are also composite fields in nature — the proton field, for instance — that are not elementary, and can be understood as built from more elementary fields. And at any given time we do not know that what appears to be an elementary field really is one, because future experiments might reveal it to be composite — just as people once thought the proton might be elementary, but then learned through experiment that it is not. And maybe fields are in fact made from something else; there have been plenty of speculations about that, but no evidence one way or the other.
So part of the problem in answering your question is that I can only give you our most recent viewpoint on what is and isn’t elementary. But in quantum field theory, the elementary fields (whatever they are) are the basic ingredients.
A field (elementary or not) in physics [not the same use of the word as in mathematics] is a function of space and time. More experimentally, a field’s “value” (i.e., how big or small the field is) is something that I can measure at every point in space, and at every time — (or at least, something I can measure over a large region of space and time.) Typical examples: density of air, wind velocity, electric fields, temperature of water, etc. Give me a point in space and time, and (assuming that I can actually do the measurement) I will give you a number, or set of numbers, that represent what the field’s value is or was at that moment and that location. And typically, a field is something which changes continuously according to given rules — differential equations, to be more technical — that can allow me to use the field’s value everywhere and now (and, also, its value just a moment ago) to predict what its value will be in the future [within the constraints of quantum physics, which doesn’t allow perfect prediction.]
Why is the wave on the strip quantized by Neumann boundary conditions, rather than Dirichlet? (ie. shouldn’t the wavefunction go to zero at the endpoints?)
In other words, why didn’t I make the waves go to zero at the edges (the way the waves on a violin string go to zero at the bridge and at the top of the neck)? The answer is pedagogical: my chain of examples in all the preceding articles used water waves in a canal as the key analogy. And of course such waves do not go to zero at the edge. But you are right that different types of extra dimensions, and even different particles in the same extra dimensions, may act differently. It doesn’t change my qualitative conclusions.
Thank you for the explanation.
Is there in today’s physics a concept of quantum of time?
There isn’t a strict notion of a quantum of space or of time — if what you mean by “quantum” (in distinction to the meaning of the term “quantum” that was used in this article) is a smallest possible jump.
First, time is not a field, and it does not have quanta the way fields do.
An electric field has waves, those waves are made from quanta (in the meaning of the term used in the article.) Time and space are where fields live.
Now, of course, gravity is a result of a gravitational field, and there is a gravitational quantum (a “graviton”) which is a ripple in space-time. But that ripple is not in any sense to be though of as the smallest-possible-bit of time — it’s a totally different thing.
It might well be that, in the full theory of quantum gravity, that time and space themselves have interesting quantum mechanical properties that include a smallest possible distance and a smallest possible length of time. But whether or not these can be thought of as similar somehow to quanta is far from obvious. For example, in string theory you cannot make extra dimensions smaller than the string scale; there is a smallest possible length for an extra dimension. But neither must the length be a multiple of the minimum size; 1.823 times the minimum length is perfectly ok for the size of an extra dimension.
In other words, the length is NOT quantized; it need not be either the minimum size or twice the minimum or three times the minimum, but can be anything in between, as long as it is bigger than the minimum.
Huh ?
Why can the extra dimensions not be smaller than the string scale ?
I mean Prof. Susskind said in an online lecture that the string scale is assumed to be at most about 1000 times the Planck scale, so why can the size of the extra dimensions not lie between these two scales in principle ?
I don’t have time to answer this question properly today or very soon, but the answer is your first hint that the world of string theory is much, much deeper than it looks at first. [Even those who might hate what string theory did to high energy physics must be truly hard-headed if they don’t admire this theory.]
Start here
http://en.wikipedia.org/wiki/T-duality
It isn’t written well for the layperson, and raises many questions, but you in particular probably know enough to get the point. Sometime soon I’ll write a short article answering this question, with pictures and diagrams that help make the point much clearer.
Thanks a lot Prof. Strassler
So it is T-duality that comes in here …?
The Wikipedia link is good, it nicely agrees whit what I`ve learned from Prof. Susskind.
To keep happy learning more about some cool physics just for the heck and the fun of it, I`ve started to avoid places (in the internet) where the hard-headed sourballs usually gather. This works well to avoid being upset and annoyed, if they dont pop up too often at places where I dont expect them at least …
Unfortunately I got recently forced to take a time-out from reading my string demystified book (which is a little bit technical) to mend some mathematical weak spots of mine first before I proceed …
So I look forward to enjoy the article with the pictures and diagrams to keep in touch with physics I like 🙂
Cheers
Hi Matt,
The historical part was an important ingredient for my self and I think this article below will help some understand that history. I appreciate the efforts you have gone through with which to explain this subject.
“After having formulated general relativity Albert Einstein did not immediately focus on the unification of electromagnetism and gravity in a classical field theory – the issue that would characterize much of his later work. It was still an open question to him whether relativity and electrodynamics together would cast light on the problem of the structure of matter.” Einstein and the Kaluza-Klein particle by Jeroen van Dongen- http://cdsweb.cern.ch/record/466266/files/0009087.pdf
A distinction that was brought up in my own observation was that this subject was more about “super gravity” then String theory, and “the circle” was more about the “distance around the circle” which seemed relevant to the size of the dimension? http://profmattstrassler.com/articles-and-posts/some-speculative-theoretical-ideas-for-the-lhc/extra-dimensions/how-to-look-for-signs-of-extra-dimensions/kaluza-klein-partners-why-step-2/#comment-5609
“If string theory is right, this is physically identical to the familiar dimensions being circular with incredibly tiny radii of about 1/R=1/1061=10-61 times the Planck length! There are our well-known familiar dimensions in an alternate description provided by string theory. [Greene’s emphasis]. In fact, in the reciprocal language, these tiny circles are getting ever smaller as time goes by, since as R grows, 1/R shrinks.” (Greene, The Elegant Universe, pages 248-249)
In a sense it was more the understanding that when one looks at the cosmos with such an articulate view of such geometrical constructions there is a far reaching connection to how one is seeing the cosmos from a microscopically considered position and that they were intrinsically connected? Would you agree?
Best,
“A black hole is an object so massive that even light cannot escape from it. This requires the idea of a gravitational mass for a photon, which then allows the calculation of an escape energy for an object of that mass. When the escape energy is equal to the photon energy, the implication is that the object is a “black hole.””
http://2.bp.blogspot.com/_cldxKGOzgeM/RgvqNYHLZ_I/AAAAAAAAAaM/ehAmOtJ0LTk/s1600/bh5.gif
…..gravitational mass for a photon?
Understanding why nothing escapes a black hole certainly does not require an idea of “gravitational mass” for the photon. You can do all sorts of things with the math, but in my view and most of my colleagues, the clearest way is just to understand it as a consequence of the geometry of space time. Massless or massive particles traveling within that geometry simply are unable to return, once they enter the black hole. This is not the only way to look at it, but “gravitational mass” sounds deeply confusing and misleading, and only useful for an observer sitting outside the black hole, whereas thinking about the geometry of space-time is clear to all observers.
[Host’s note: Commenter intended this as a reply to embercadero]
I’m not an expert by any means so anyone is free to correct me if I get something wrong but here’s what I remember reading about extra dimensions and how they got started.
Back around the 1920s (give or take) after Einstein formulated his theory of relativity there was some talk of trying to unify gravity with electromagnetism. Two theorists, Kaluza and Kein, came up with a pretty elegant theory that combined gravity and electromagnetism in a such a manner that when when Maxwell’s Equations were written in terms of 4 spatial dimensions out popped Einstein’s equations of Relativity. The Kaluza-Klein theory was eventually disproved for reasons that elude me at the moment but their work did get physicists and mathematicians thinking about higher spatial dimensions.
That’s my dime store remembrance of it all. You could probably find a much more thorough explanation elsewhere online or in a books.
That’s almost right, except that you have one thing reverse:
“Kaluza and Klein… came up with a pretty elegant theory that combined gravity and electromagnetism in a such a manner that
when Maxwell’s Equations were written in terms of 4 spatial dimensions out popped Einstein’s equations of Relativity.no, when Einstein’s relativity was written in 4 spatial dimensions, out popped Maxwell’s equations.It’s easy to get electromagnetism from gravity, but the reverse is not true.
I didn’t put this history into the current articles mainly because I didn’t have time yet to make sure I get it exactly right.
How large would the extra dimension need to be for the Large Hadron Collider to see an extra dimension?
(Guessing, 10^-18 m.)
Which sizes of extra dimensions have been ruled out due to lack of effects/observations?
jal
That will be the next set of articles; your guess is right for certain classes of extra dimensions, but for other classes it is far too pessimistic.
Thanks for this series of articles. I am amazed at how straight forward this all seems with your explanation. Even while reading the previous article, I had more or less guessed the reason the apparent M masses were quantized. My favorite part of this installment was when I said to myself, “Wait, could any known particles be KK partners of other known particles?” And then the very next paragraph was you answering that exact question. I also enjoyed your explanation of particles i.e. quanta. In reading this stuff from various sources, I had come to the same conclusion, that if I thought of these things first as waves they seem a lot less mysterious!
In the past, I have heard string theory skeptics (physicists) cite the requirement for unknowable extra dimensions as a reason string theory was too out there to be taken seriously, but this seems to render that argument toothless. I realize extra dimensions don’t imply string theory, but nonetheless this is a prediction that string theory makes that is testable.
When you say that a particle with momentum in extra dimensions would appear to have more mass to a naive 3D observer, are there gravitational implications of this? Could this be dark matter? I am guessing the answer is, we don’t know because we have no theory of gravity at the quantum level. In general relativity, mass warps spacetime. In principle, would this “naively experienced” mass act like “real” mass in this regard?
Let me not address the string theory physics and politics here — the situation is complex, more than you have stated. I’ll do that at another time. Suffice it to say that the existence (or not) of extra dimensions is an experimental question, not a theoretical one.
In Einstein’s theory of gravity (general relativity), it is really energy and momentum that warp space-time, not mass directly. The reason that we think (and talk) about mass doing the job is because a particle at rest (or moving slowly) has very little momentum, and the energy it has is all mass-energy (E=mc2 energy). So for the sun and the planets and galaxies, the warping effect is proportional to mass. But light (massless, but energetic) can warp spacetime too.
So if I see a photon moving in an extra dimension that I know about, I’ll describe it as warping space by an amount related to its motion-energy. Meanwhile, if you don’t know about the extra dimension, and the photon seems to be a stationary but massive KK partner to you, you’ll see it warp space in the same way, by an amount proportional to what you think is mass-energy. It doesn’t matter that I think the photon’s energy is motion energy and you think that same energy is the mass-energy of a KK partner of the photon. The gravitational effects (at least in the large dimensions) are the same.
Dark matter is probably made from particles. Those particles might be KK partners of the photon (i.e., photons moving in an extra dimension.) But there are many other possibilities for what dark matter might be.
My understanding is that dark matter doesn’t interact with light (hence the name). Would this be true of a KK partner of a photon? I’d have assumed that KK partners would interact with the same forces as the ‘normal’ particle.
Photons do not interact directly with each other (which is why lasers are not disrupted by sunlight, for instance.) And so KK partners of the photon do not interact with photons either.
Of course, photons do interact with ordinary matter. But KK partners of the photon would typically interact in a way that involves both ordinary matter and the KK partners of ordinary matter… for instance, the collision of a KK partner of the photon and an electron would produce a KK partner of the electron … and since the partners of ordinary matter are also very heavy, any resulting indirect interactions with ordinary matter would be extremely weak.
Thanks, Matt. This is great. I did not understand light too warps spacetime. It’s going to take some time to wrap my head around the implications of that even without hidden dimensions. This seems to imply that if you fired a powerful enough laser that you could in fact generate gravity.
Nice post, it’s great to have a well explained description of topics like this.
One little typo though: “In both cases there is a largest possible wavelength (1/S for the tube, 2/W for the strip).” You mean a wavelength of S and W/2 I assume.
Thanks! And it was worse than that; I had W/2 instead of 2W in many equations… hopefully all fixed now.
Oh yeah, 2W. I should have noticed that too!
Hi Matt
I missed one thing in this excellent series of aricles. What was the initial reason that physicists started thinking that nature may have more spatial dimensions than 3? Was there any particular reason for such suspicion, coming from experiment or other theories, or was it just someone’s “let’s see what happens if…” kind of thinking?
Yes, I probably should have addressed this. Look at Carmen’s reply below, which gives an answer which is basically right (except for one mistake, which I corrected in my reply.) I just haven’t set up my articles in an order that makes it easy to explain this point yet.
2 questions:
1) On a tube there are 2 directions for waves to travel around. Both have the same mass but 2 of the same direction would interact in a different way than 2 of different direction, right? Is there something like special relativity for such a particle (seeing the same-direction particle as a “simple” particle and the different-direction particle as having twice the minimum momentum?)
2) What if extra dimensions have planck scale size? My first guess is that kaluza-klein partners would have masses at planck scale, too. But couldn’t in that case gravitaitonal effects totally mask the extra-dimension effects?
1) Good question; in the case of the tube, there are, as you say, always two KK partners with the same mass, one going around the tube one way, one going around the other way. These are related by a symmetry. We know of many examples in nature of particles that are very similar in their properties and have exactly or nearly the same mass, and that is because of an exact or approximate symmetry. For example, the positively charged pion and negatively charged pion have exactly the same mass, because they are related by the (believed-)exact symmetry known as CPT; the uncharged pion has nearly the same mass, because the three pions are related by an approximate symmetry, which would be exact if the up and down quarks had exactly the same mass.
2) If extra dimensions have Planck-scale size, then indeed quantum gravitational effects will be important and I don’t know what will happen. What I’ve told you assumed the extra dimensions were larger than that.
Interestingly, in string theory, the smallest size you can have for extra dimensions is string-scale, which is always larger than Planck scale (though possibly not by very much); if you try to make the dimensions smaller, the physics becomes very complicated from one point of view, but it turns out there is a different point of view which is simpler, and from that point of view the dimensions are getting bigger, not smaller. Weird! But very important — and a very deep subject indeed, far beyond what I can explain with what is currently on the website… But probably Brian Greene must mention this in his first book, though I can’t recall it.
Hi Matt,
Firstly I’d like to thank you for the amazing articles you’ve put up here – I stumbled across them yesterday and they’ve already been of great help and interest to me. I have a slight question about your response above regarding the symmetry you mention (that relates the two KK partners with the same mass travelling around the tube in opposite directions. Is this the symmetry that gives rise to KK parity? And if so, is the fact that it is due to these two particles the reason why the total KK number entering any vertex is forced to be even?
Cheers for the help!
Yes — with one addendum.
KK parity is a symmetry that arises when flipping the extra dimension “left-to-right” leaves it looking the same, in which case KK modes have a parity quantum number that has to be even in any interaction — i.e., the interactions have to be left-to-right symmetric. This would be true, for instance, if the extra dimension were an interval — a finite distance with two reflecting walls. Or if there were two extra dimensions with a non-isoceles triangle. [If it were isoceles there would be a order-six symmetry! — the rotations by 120 and 240 degrees combined with flips left-to-right.]
Specifically for a circular extra dimension: the symmetry is even stronger because there is translation invariance around the tube, so there is a momentum quantum number for motion in the compact direction that can be any integer. This is a case with a U(1)_KK symmetry. In this case every KK partner has an integer charge associated with it, no just an even or odd parity; and those charges have to add up to zero in any interaction. So that is stronger than KK parity, where things just have to be even under the parity. On a torus (two circles combined together) there would be two such symmetries. Other symmetries arise on other regular surfaces, such as spheres. The general question is: what is the symmetry of the extra dimensional space? the KK modes will have charges under that symmetry group and the interactions will have to respect that symmetry.
let me guess the answer will be periodic boundary conditions(for something like a rolled up dimension). These periodic boundary conditions will mean that so you have a continuous function the impulse k(using the natural unit system) will have to be a mutiple of pi divided by the length of the dimension(so the wavefunction is continuous). For straight bountary conditions the particle cannot reach outside the length of the dimension so the wavefunction needs to be 0 at the ends of the dimension. This means k must be multiples of pi/2 divided by the length of the dimension.
Is that right? I am guessing before you wrote your article.
You’ve got the basic idea; it’s just details from there. What we call a “particle” is really a “quantum” — a ripple in a quantum field that has the minimal allowed intensity — and a quantum is sufficiently wave-like that when moving with low momentum in a dimension of finite length, it behaves more like a wave than a particle… with the consequence that only certain momenta are allowed. Now I have to figure out how to explain that slowly, with pictures.