Of Particular Significance

Zero-Point Energy of Fields (Part 2)

© Matt Strassler [February 19, 2024]

This article is the fourth in a series on zero-point energy; here’s the first, the second, and the third. The last of these covers the zero-point energy of a simple class of fields: bosonic fields whose corresponding particles have zero mass. Here we’ll move on to look at other fields: fields whose particles have mass, and fermionic fields. Along the way we’ll encounter the idea of “supersymmetry”, which proves useful conceptually even if it is not true in nature.

[For brevity, throughout this article, I’ll use the word “mass” to mean “rest mass”.]

If the Field’s Particles Have Mass

How does zero-point energy work for a field that has a non-zero resonance frequency $f_0$ , and thus has particles (i.e. wavicles) with rest mass $m_0$ , where the two are related by

$m_0 = f_0 \frac{h}{c^2}$

Here $h$ is Planck’s constant (the cosmic certainty limit) and $c$ is the cosmic speed limit, also known as “the speed of light”. (The origin of this relation between mass and frequency is carefully explained in the first two-thirds of Waves in an Impossible Sea.)

Examples of bosonic fields with a non-zero resonance frequency would include the W field, the Z field, and the Higgs field itself. We’ll come back to fermionic fields, such as the electron field, in the next section.

Compared to the previous article, which described what happens when $f_0=0$ (and therefore $m_0=0$ ), the zero-point energy of known fields doesn’t change very much. There’s just a tiny shift, one that depends on $f_0$ . Specifically, the zero-point energy density $\rho$ (the energy found in a region divided by the region’s volume) is now

$\rho \approx \# \frac{hc }{\ell_p^4} \left(1+f_0^2 \ell_p^2/c^2\right)$

where $\#$ represents a numerical constant that we don’t care about, and $\ell_p$ is the ridiculously tiny Planck length, about 10^-35 meters. This formula is discussed in somewhat more detail at the end of this article.

More revealingly, we can write this in terms of the mass $m_0$ of the particles associated to the field, and the Planck mass $m_{pl}$ , which is about 10¹⁸ times larger (i.e. a billion billion times larger) than a proton’s mass:

$\rho \approx \# \frac{hc }{\ell_p^4} \left(1+m_0^2 /m_{pl}^2\right)$

[I use a subscript-“pl” here for “Planck” rather than “p”, because m_p is often used to refer to the proton’s mass.]

Since all known elementary particles’ masses are less than a thousand times a proton’s mass, $m_0/m_{pl} < 10^{-15}$ for all known particles. For most purposes, we can easily ignore this incredibly tiny shift in the zero-point energy density.

And yet, in the universe we live in, that shift is very important.

For every known elementary field with a non-zero resonance frequency, that frequency (along with the mass of the corresponding particle) depends upon the average value of the Higgs field; and therefore, the field’s zero-point energy, too, depends upon the Higgs field ‘s value.

As we will see in the next article in this series, this is the origin of the hierarchy puzzle.

In short, as argued (without math) in Chapter 23 of Waves in an Impossible Sea,

quantum field theory predicts a huge zero-point energy (or vacuum energy) for each field, and
if that field’s stiffness depends on the Higgs field’s average value, then its vacuum energy does too.

The latter then feeds back on the Higgs field’s behavior, and specifically on its own stiffness and resonance frequency, leading to the hierarchy puzzle. But we’re getting ahead of ourselves; more on this in the next article. We have other things to do first.

Bosonic Fields vs. Fermionic Fields

So far, all my calculations have been appropriate for elementary bosonic fields, whose particles are elementary bosons — photons, W bosons, Z bosons, gluons, and Higgs bosons (assuming the latter really are elementary.) For elementary fermionic fields, whose particles are fermions — electrons, muons, taus, neutrinos and quarks — the calculation is almost the same, except for a crucial minus sign.

$\rho_{\rm fermionic} \approx {\bf -}\# \frac{hc }{\ell_p^4} \left(1+f_0^2 \ell_p^2/c^2\right) = {\bf -}\# \frac{hc }{\ell_p^4} \left(1+m_0^2 /m_p^2\right)$

The origin of the minus sign goes all the way back to the zero-point energy for a single ball on a spring; such an object is a boson, and has zero-point energy $+\frac12 f h$ , where $f$ is its frequency. More generally, a vibrating bosonic object is called a simple harmonic oscillator. There is a fermionic version of such a thing, whose zero-point energy is negative: ${\bf -}\frac12 f h$ . The standing waves in a bosonic field each have a positive zero-point energy, while those in a fermionic field have negative zero-point energy, but otherwise the calculation is the same.

Could Bosons and Fermions Cancel Each Other Out?!

This observation might naturally lead you to wonder about a possible solution to the cosmological constant problem (which was briefly described in the previous article.) The problem is that the zero-point energy density of each cosmic field is gargantuan when compared with the measured total energy density of empty space. (We know this because a large zero-point energy density would be expected to cause the universe to expand at spectacularly high rate.) Perhaps, if the universe had exactly the same number of fermionic fields as the number of its bosonic fields, the former contributing negative zero-point energy and the latter positive zero-point energy, their zero-point energies would cancel out, and the total energy-density of empty space would be zero, or very nearly so.

Remarkably, this clever idea can be turned into full-blown math, under the name “supersymmetry”. Were this symmetry an exact or even approximate property of nature, it would assure that for every bosonic field, there would be a fermionic field with similar properties. (Jargon: these two fields are referred to as each other’s “superpartners”.)

This is a promising notion and brilliant mathematics. But… it wouldn’t solve the cosmological constant problem, not in a universe like ours, anyway.

A serious failing (though not the only one) is that for the cancellation to occur, not only should there be one fermionic field for each bosonic field, but also they would have to have exactly the same resonance frequencies. Equivalently, the masses of their respective particles would have to be identical. If you had a bosonic field with resonance frequency $f_B$ and a similar fermionic field with resonance frequency $f_F$ , the sum of their zero-point energy densities would be

$\rho_B + \rho_F \approx \# \frac{hc }{\ell_p^4} \left[\left(1+f_B^2 \ell_p^2/c^2\right)-\left(1+f_F^2 \ell_p^2/c^2\right)\right] =\# \frac{h}{c\ell_p^2} \left[(f_B^2-f_F^2)\right]$

If the two frequencies aren’t equal, then the answer isn’t zero. We can write it as

$\rho_B + \rho_F \approx \# \frac{hc }{\ell_p^4} \left[(m_B^2-m_F^2)/m_{pl}^2\right]$

If both particle masses are far less than the Planck mass, then this $\rho$ would be much smaller than we’d find for either field separately. But to get (almost) zero $\rho$ we’d need the two superpartners to have (almost) identical mass, i.e. $m_B = m_F$ . Otherwise the cancellation is incomplete, and there’s still lots of zero-point energy density left over, far more than inferred from the universe’s changing expansion rate.

Exact supersymmetry would indeed predict $m_B = m_F$ for every superpartner pair, so the cancellation would be perfect. But experiment clearly shows that this just isn’t true in nature. For instance, the electron (a fermion) would have to have a superpartner, a boson usually called the selectron, which would be electrically charged like the electron, and whose mass would be almost identical to that of the electron. Such a particle would easily have been observed even a century ago.

At best, only a rather approximate form of supersymmetry, in which superpartners of known particles do exist but have masses that are significantly larger, might be true of our world. In such a form of supersymmetry, the zero-point energy density cancels only partially, and the cosmological constant problem is not resolved.

Still, such partial cancellations from imperfect supersymmetry could have been good enough to address another issue: the hierarchy puzzle. I’ll discuss this in some detail in the next article in this series, but in brief, this would have required that typical superpartners of known particles have masses between 100 and 1000 times the proton’s mass. But were this true, the ongoing experiments at the Large Hadron Collider [LHC] ought to have discovered at least one type of superpartner particle by now, and probably many more. None have been found, and so yet again, experiment says “no”.

Nevertheless, when one is trying to understand the nature of the hierarchy puzzle, the fact that supersymmetry could have resolved it is conceptually useful. For this reason, we’ll look at it more closely in the following article of this series.

The Effect of a Resonance Frequency: The Details

Now let’s quickly dive into the math behind the claims in the first section above. In terms of the resonance frequency $f_0$ , the calculation of the zero-point energy is almost the same as for a field with $f_0=0$ , presented in the previous article in this series. We have the same sum over standing waves

$E_{{\rm zero-point}}^{{\rm total}} = \sum_{q_1=1}^{q_{{\rm max}}} \sum_{q_2=1}^{q_{{\rm max}}} \sum_{q_3=1}^{q_{{\rm max}}} \frac{1}{2}q f h$

but our formula for $q$ changes from

$q=\sqrt{q_1^2+q_2^2+q_3^2}$

$q=\sqrt{q_1^2+q_2^2+q_3^2 + (f_0L_u/c)^2}$

which follows from a change in the wave equation.

Notice that when $f_0=0$ , this does indeed agree with the formulas in the previous article. But there’s something new; we can set $q_1=q_2=q_3=0$ . Then the field’s standing wave has no distinct crests or troughs; it consists only of the field vibrating uniformly. This is pure resonance: the standing wave vibrates with the field’s resonance frequency $f_0$ . (See Chapter 17.1 of Waves in an Impossible Sea, notably Fig. 41, and Chapter 20.2, notably Figure 48 at right.)

Click here to learn the change in the wave equation and what happens with 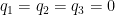$q_1=q_2=q_3=0$

The wave equation for a field $\phi(x,y,z,t)$ with a resonance frequency is

$(\partial\phi/\partial t)^2 - (\partial\phi/\partial x)^2 - (\partial\phi/\partial y)^2- (\partial\phi/\partial z)^2 + f_0^2 \phi= 0$

which reduces, when $f_0=0$ , to the wave equation encountered in the previous article. With this change, there is a new solution that is absent when $f_0=0$ , namely one that does not depend upon $x$ , $y$ , or $z$ at all:

$\phi(x,y,z,t) = \sin(2\pi f_0 t)$

which is the same sort of solution one would write for a ball on a spring, vibrating at its resonance frequency $f_0$ . The whole field vibrates together, like a ball on a spring. With minimal possible amplitude, such a vibration would correspond to a single, stationary wavicle of the field $\phi$ .

As for $f_0=0$ , as shown in the previous article, the sum again is proportional to the maximum possible $q$ to the fourth power. But there is a small shift because of the changed formula for $q$ :

$\rho \approx E^{{\rm total}}_{{\rm zero-point}}/L_u^3 \approx \# \frac{hc }{\ell_p^4} \left(1+\frac{f_0^2 \ell_p^2}{c^2}\right) \approx \# \frac{hc }{\ell_p^4} \left(1+\frac{m_0^2}{m_{pl}^2}\right)$

Click here to see how to estimate the correction:

There are various tricks that would give an estimate. One way to do it is to notice to replace the sums with integrals and just do the integration. Another is to write the first term of a Taylor series:

$q=\sqrt{q_1^2+q_2^2+q_3^2 + (f_0L_u/c)^2}\approx \sqrt{q_1^2+q_2^2+q_3^2} + \frac12(f_0L_u/c)^2/\sqrt{q_1^2+q_2^2+q_3^2}$

and use the facts that (in the notation of the previous articles)

$\sum_{q_1=1}^{q_{{\rm max}}} \sum_{q_2=1}^{q_{{\rm max}}} \sum_{q_3=1}^{q_{{\rm max}}}\ \sqrt{q_1^2+q_2^2+q_3^2}\sim q_{max}^4 \sim (L_u/\ell_p)^4$
$\sum_{q_1=1}^{q_{{\rm max}}} \sum_{q_2=1}^{q_{{\rm max}}} \sum_{q_3=1}^{q_{{\rm max}}}\ (1/\sqrt{q_1^2+q_2^2+q_3^2})\sim q_{max}^2 \sim (L_u/\ell_p)^2$

from which the claimed result can be obtained.

For all known elementary particles, the ratio $m_0/m_{pl}$ is tiny, and so the correction to the energy density is extremely tiny too; but it depends on the Higgs field’s average value, and that will play a central role going forward.

Zero-Point Energy of Fields (Part 2)

If the Field’s Particles Have Mass

Bosonic Fields vs. Fermionic Fields

Could Bosons and Fermions Cancel Each Other Out?!

The Effect of a Resonance Frequency: The Details

Leave a ReplyCancel reply

Recent Posts

Buy The Book

Reading My Book?

Media Inquiries

Zero-Point Energy of Fields (Part 2)

If the Field’s Particles Have Mass

Bosonic Fields vs. Fermionic Fields

Could Bosons and Fermions Cancel Each Other Out?!

The Effect of a Resonance Frequency: The Details

Leave a ReplyCancel reply

Recent Posts

Buy The Book

Reading My Book?

Media Inquiries

Order Waves In An Impossible Sea