MATT STRASSLER
Of Particular Significance

Zero-Point Energy of Fields (Part 1)

© Matt Strassler (February 15, 2024)

This article is preceded by two others, which show that

  • the zero-point energy of a ball on a spring is E=\frac12 f h, where f is the frequency of the ball’s vibration and h is Planck’s constant (the cosmic certainty limit) ;

  • the zero-point energy density of a guitar string (its zero-point energy divided by its length) is independent of its length, and is given by \rho_0\approx hv/\ell^2, where v is the speed of the guitar string’s traveling waves and \ell is the minimum distance that can separate one wave crest from another, which may be the distance at which the internal structure of the string becomes important.

Overview

Now we will turn from the guitar string to a cosmic field — an entity found everywhere in the universe, across all its three dimensions of space. (The classic example is the electromagnetic field [which is just the electric field and the magnetic field of the universe, thought of as a single entity.] ) As I’ll explain later in this article, the arguments I made for the guitar string, when modified for fields, show that the zero-point energy density of a field is

  • independent of the size of the universe, and
  • inversely proportional to a power of \ell

But whereas we found \rho_0\approx hv/\ell^{{\bf 2}} for a guitar string, for a field in three spatial dimensions we have a different power of \ell

  • \rho_0\approx hv/\ell^{{\bf 4}}

For a field of the universe, the wave speed v in question is the cosmic speed limit c, while the shortest distance that we can hope is meaningful for the universe is the ridiculously small Planck length \ell_p, approximately 10-35 meters. This gives us, for a cosmic field,

  • \rho_0 \approx hc/\ell_p^4 = 10^{114} \ {\rm Joules \ per \ cubic \ meter}

That’s an absurdly large amount of energy! If we could (but we can’t!!!) convert this zero-point energy to mass via E=mc^2, this would correspond to 1097 kilograms, more than the mass of all the stars in the visible part of the universe! … and that’s in one cubic meter, smaller than your bedroom!

You might well guess that so much energy in such a moderate space would collapse gravitationally and form a black hole. Surprisingly, however, this is not the way gravity works.

Thanks to Galileo’s principle of relativity and Einstein’s modification of it, this positive energy density has to be accompanied by negative pressure, of the same size. And thanks to Einstein’s theory of gravity, the response of gravity to such a large negative pressure would be to cause the universe to expand at an incomprehensibly fast rate. In an instant, the universe would be gigantic beyond imagining, and much more empty than it is. This would be cosmic inflation, at the fastest possible speed.

Clearly, if you look around you, you see this isn’t happening. So something is wrong. This is the first indication of what is known as the cosmological constant problem. Either

  • our calculation of a single field’s zero-point energy density (and the negative pressure that goes with it) is wildly in error, or
  • when you add together the zero-point energies of all the universe’s fields, they somehow almost perfectly cancel each other, or
  • gravity doesn’t behave quite the way Einstein thought it did, or
  • …well …maybe there’s something more clever going on, perhaps something that no human has yet thought of.

Bosonic Fields with Massless Particles

Now, what justifies all these statements? Fortunately, we are still able to use pre-university math, except at one step, which is explained in an aside that you can read or skip as you like.

While a string extending in just one direction has standing waves with a certain number of crests or troughs that follow each other in one dimension, a standing wave for a field in a three-dimensional box has crests and troughs in three dimensions.

This is hard to draw, so for intuition, let’s look at a vibrating, square-shaped rubber sheet in two dimensions. As you can see in the figure below, the crests and troughs form a two-dimensional grid. The total number of crests and troughs on the grid is a product of two integers: the number of crests and troughs along one direction times the number of crests and troughs along the other direction.

A two-dimensional standing wave inside a square; its troughs and crests form a grid. The numbers q1 and q2 count the numbers of troughs and crests found along any line that crosses the square in the two directions, with the total number of troughs and crests equaling q1q2. In waves within three dimensions, three such numbers are needed.

In three dimensions, we will have a three-dimensional grid, and so the total number of crests and troughs is a product of three integers. So instead of the single sum over one-dimensional standing waves

  • E^{{\rm total}}_{{\rm zero-point}} = \sum_{q=1}^{q_{{\rm max}}} \frac{1}{2} q f h

that we had for our one-dimensional string, we will now have a sum over three-dimensional standing waves

  • E_{{\rm zero-point}}^{{\rm total}} = \sum_{q_1=1}^{q_{{\rm max}}} \sum_{q_2=1}^{q_{{\rm max}}} \sum_{q_3=1}^{q_{{\rm max}}} \frac{1}{2}q f h

which is very similar to what we had for a guitar, except that q is no longer an integer, and is instead

  • q=\sqrt{q_1^2+q_2^2+q_3^2}

The expression in square roots can be obtained by looking at the equation that governs simple waves. (The precise expression isn’t crucial; we’d get the same rough answer below if q were instead equal to \ ~q_1+q_2+q_3, or any other reasonable guess. But we may as well do it correctly.)

I have also assumed, in writing this expression for q, that the field whose zero-point energy we are computing has no resonance frequency. As carefully explained in Waves in an Impossible Sea, such a field has “particles” [or more accurately, “wavicles”] whose rest mass is zero. In this situation, the field’s lowest possible frequency f is set by the distance across the universe L_u and the cosmic speed limit c at which traveling waves travel, f=c/L_u. (We’ll come back to the case with a non-zero resonance frequency in the next article in this series.)

Click here to learn why we get the above square-root formula for q and why f=c/L_u:

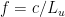Here’s the only place where we need university-level math. The wave equation that governs a wave in a field \phi(x,t) inside a box of length L in one dimension, with waves subject to the cosmic speed limit, is

  • (d\phi/d t)^2 - c^2(d\phi/d x)^2 = 0

(where, strictly speaking, these derivative symbols ought to be partial derivatives, but that has no practical impact here.) The solution is a standing wave,

  • \phi(x,t) = \sin(2\pi f_q t) \sin( q \pi x/L) \ ,

where q must be an integer if the field is to vanish at the edges of the box. Plugging this solution into the wave equation implies

  • (2 \pi f_q)^2 - c^2(q \pi /L)^2 = 0

and thus the frequency has to be an integer times the lowest frequency f = c/2 L:

  • f_q = q c/ 2 L = q f

Now let’s repeat this for a wave in three dimensions, in a box whose sides have length L_u. The wave equation becomes

  • (\partial\phi/\partial t)^2 - (\partial\phi/\partial x)^2 - (\partial\phi/\partial y)^2- (\partial\phi/\partial z)^2 = 0

and for a solution

  • \phi(x,t) = \sin(2\pi f_q t) \sin( q_1 \pi x/L_u) \sin( q_2 \pi y/L_u) \sin( q_3 \pi z/L_u)

the wave equation gives

  • (2 \pi f_q)^2 - c^2(q_1 \pi /L_u)^2- c^2(q_2 \pi /L_u)^2- c^2(q_3 \pi /L_u)^2 = 0

and so the frequency of the wave is now

  • f_q= \sqrt{q_1^2+q_2^2+q_3^2} (c/2L_u) = \sqrt{q_1^2+q_2^2+q_3^2} f

which was what we were trying to prove.

The final answer in this case is then, approximately, given by the three sums. Whereas one sum over q gave us something close to q^2/2, the three sums over q_1, q_2, q_3 give us something close to q^4 (as you can verify yourself with a programmable calculator). The conclusion is that, as claimed earlier,

  • E_{{\rm zero-point}}^{{\rm total}} \approx \# q_{{\rm max}}^4 fh

where \# represents a numerical constant that we won’t need to care about.

In the previous article in this series, I estimated the maximum q for a string’s standing wave in terms of

  • the length L of the vibrating object, and
  • the length scale \ell at which we expect to see some kind of substructure or breakdown of the object

This formula continues to apply here for a field, with the overall length being the distance across the universe L_u, and the short length scale where the notion of space itself may break down being the Planck length \ell_p). Roughly speaking, then,

  • q_{{\rm max}} \sim L/\ell = L_u/\ell_p

Since f=L_u/c for the lowest frequency of the field in a box with sides of length L_u, our expression for the zero-point energy now becomes

  • E_{{\rm zero-point}}^{{\rm total}} \approx \# {L_u^4 f h}/{\ell_p^4} = \# {L_u^3 h c}/{\ell_p^4}

and so, as claimed earlier, the energy density — the zero-point energy of the field per unit volume — is

  • \rho_0 \approx E^{{\rm total}}_{{\rm zero-point}}/L_u^3 \approx \# {hc}/{\ell_p^4}

As noted above, that’s an astounding 10114 Joules in every cubic meter of the universe!!!

What Does All This Energy Do? The Cosmological Constant Problem

You might think that you could now use Einstein’s relativity formula E=mc^2 and learn that the field’s zero-point energy contributes an insane 1097 kilograms of mass for each cubic meter of space. 1097 kilograms is far, far more than the mass of all the stars in the universe — far more than needed to create a black hole in such a small region. And your conclusion would be correct, if you could think about a cubic meter of space as though it were a stationary object, one to which E=mc^2 would apply.

But space is not an ordinary, stationary object; it must obey Galileo’s relativity principle, which states that you cannot say whether you are or are not stationary relative to empty space. This means that the empty space of the universe doesn’t satisfy the rules that would allow you to apply Einstein’s simple relativity formula to it. (These points are addressed in some detail in Waves in an Impossible Sea. In particular, despite certain naive intepretations of E=mc^2, energy and mass are not always the same thing.)

Instead, remarkably, Galileo’s and Einstein’s relativity principles require that space have not only energy density but also pressure . . . and that this pressure be equal to minus the energy density. If this were not the case, then you could measure your motion relative to empty space, and the principle of relativity would be violated.

Why is this true? Click here for some insight

The point is that in the presence of energy density \rho and uniform pressure p, the energy-momentum tensor T_{\mu\nu}, mentioned in the next paragraph, is a 4×4 diagonal matrix with entries \{\rho,p,p,p\}. But steadily moving observers will not all see it that way. An ordinary gas has \rho \gg p > 0, and you know from experience that it violates the relativity principle: the wind you feel when you move through air certainly reveals your motion! For a substance or a substance-like thing to hide its motion, giving the same energy-momentum tensor to all steadily moving observerse, requires that p=-\rho, and thus sets the energy-momentum tensor proportional to the metric tensor g_{\mu\nu}; this is the only possibility that maintains the relativity principle.

This is where it becomes important that we are dealing with Einstein’s theory of gravity and not Newton’s. Newton attributed gravity between objects to the objects’ masses. But Einstein’s theory says instead that gravity arises from energy, momentum, pressure, and so forth, all organized together in what is known as the energy-momentum tensor. (I wrote a little about that tensor here.)

In many situations, only the energy is large, and that’s the only important part of the energy-momentum tensor. Then you can use E=mc^2 to relate energy to mass, and recover Newton’s gravity formula as an approximation to Einstein’s. But this is not one of these situations.

How can we understand intuitively why gravity might cause this positive energy and negative pressure to expand, opposite to what we expect gravity to do? An ordinary gas in a box will indeed act like any ordinary object: it has energy density and positive pressure, and gravity will tend to cause it to collapse. If the gas is made of slow objects, like atoms at room temperature, the pressure will be small and positive. If the gas is made of objects moving near or at the cosmic speed limit, such as a box full of bright light, then the pressure will be +1/3 the energy density, and gravity will still cause this gas to collapse. But with negative pressure equal in magnitude to the energy density, it goes the other way. (The balance point is when the pressure is -1/3 the energy density.) As a result, for zero-point motion, the negative pressure wins over the positive energy, and gravity’s response is to cause expansion rather than contraction… and to do so exponentially fast. This is the central principle that drives what is known as cosmic inflation, which may have occurred early in the universe.

If the energy density were really 10114 Joules per cubic meter, you can’t even begin to imagine how fast that cosmic inflation would be. There’s no point in even trying; it’s beyond description. Suffice it to say that this is not happening in our universe. Measurements of the universe’s behavior show that its “dark energy” — more correctly, despite its name, the dark energy density and negative pressure of the universe — is only about 10-9 Joules per cubic meter.

It seems, then, that our calculation of the zero-point energy is either wrong, incomplete, or irrelevant. This is the cosmological constant problem. (Well, part of it, anyway.)

But our calculation isn’t wrong in an obvious way; it’s not a matter of our being bone-headedly stupid. The very same calculation of zero-point motion and zero-point energy applies (with \ell the spacing between atoms) to ordinary three-dimensional crystals. For instance, it contributes to the prediction of the temperatures at which they melt. In fact, thanks to these zero-point effects, helium atoms at standard atmospheric pressure never freeze at all, even at the lowest possible temperature (“absolute zero”). A hundred years of experiments confirm that zero-point motion and energy cause real, measurable impact on physical objects.

It’s only when we try to apply these ideas to the fields of the cosmos that we sometimes [but by no means always] run into trouble. More on that in later articles — though for now, if you’re impatient, here are two lines of thought for you to consider:

Maybe the Planck length is longer than we think?

There is one obvious place that we could be seriously wrong. I’ve assumed that Einstein’s theory of gravity, and our understanding of fields and their zero-point energy, extends all the way down to the Planck length, 10-35 meters. We have no experimental evidence that this is true. Maybe it just isn’t.

We do know that our understanding of fields is so good that not a single measurement at the Large Hadron Collider [LHC] yet conflicts with it. The LHC is our largest and most powerful particle accelerator, and its collisions test our understanding of physics down to lengths of about 10-19 meters, about 10,000 times shorter than the diameter of a proton. Let’s call that distance \ell_{LHC}. Maybe, instead of the zero-point energy being

  • \rho \approx \# {hc}/{\ell_p^4}

it should only be

  • \rho \approx \# {hc}/{\ell_{LHC}^4}

That does indeed make a spectacularly huge difference! Instead of 10114 Joules per cubic meter, we would only have 1050 Joules per cubic meter. Remember, that’s like taking a number with 114 zeroes and replacing it with one that has only 50 zeroes; it’s an enormous reduction.

And yet, it’s not nearly enough. Again, experiment shows that the total energy density of the universe is only 10-9 Joules per cubic meter. So even if our understanding of quantum fields is completely wrong at distances below those studied by the LHC, it doesn’t matter: the predicted zero-point energy, based on what we know experimentally, is still way, way too big. This is what makes the cosmological constant problem so hard; it seems to fly in the face of what we think we already know for sure.

Maybe Einstein’s gravity doesn’t work at microscopic distances?

We don’t have direct tests of gravity at distances much below millimeter scales; it’s so weak that it’s very hard to measure. For this reason, we might wonder if there’s a problem interfacing gravity with the zero-point energy below a certain distance. Then the zero-point energy would be there — our calculation of it would be correct — but gravity wouldn’t respond to it to the degree expected.

This sounds good on paper, but it proves quite difficult to make it consistent. There have been some very clever ideas about how to do it, most notably by Raman Sundrum, but as far as I know, they really only work for particles that have rest mass. In general, it’s very hard to make them consistent for light— for its particles, “photons”, that have no rest mass — and probably also for neutrinos, with very low rest mass. Briefly stated, it’s hard to modify gravity, making it dramatically weaker than expected at distances of a few tenths of a millimeter, without messing up Einstein’s principles at more familiar distances. Maybe it’s not impossible, but so far, no one has done it.

Click here for the next article in the series.

27 Responses

  1. Can cosmologists work out how much of the expansion rate of our universe is down to dark energy alone?

    How significant is the contribution to the total zero point energy from fields interacting with one another?

    Reply

    1. 1) The expansion *rate* is not due to dark energy. The change in the expansion rate is affected by dark energy and yes, that is worked out precisely, and is in fact the main way that the amount of dark energy is measured.

      2) It’s potentially as large as the zero-point energy itself. To answer the question in any detail, you need to know what the interactions are like near the Planck length scale (or whatever is the true scale at which the calculation should be stopped), but that’s not something we know. (The strong nuclear force, for instance, may be no stronger than electromagnetism at that scale. But it’s also possible that electromagnetism and the strong nuclear force are both strong, if there are additional unknown particles that have very high masses.)

      At a minimum, gravitational effects are potentially as large as any other part of the calculation, if the Planck length is the relevant scale. If the scale is much lower than that, then gravitational effects may be minimal. Or not. It depends on the details.

      Reply

  2. To compress a volume of gas isothermally one need to get rid of excessive heat generated during the compression, so its energy content can’t remain the same. If a volume of gas is compressed adiabatically, i.e. during a star collapse, its temperature rises so the energy is conserved. But several measures of gravity like surface gravity, self-gravity, space-time curvature definitely rise.

    Reply

    1. As Serge says, your example has to be thought through carefully, and the answer isn’t so simple. More generally, getting details straight in Einstein’s gravity is hard; even defining the mass or overall density of an object unambiguously can be extremely subtle and often impossible… and when it’s easy to do, its gravitational effects are often the same as in Newton’s theory unless you come close to the object.

      First, though: you notice that in discussing zero-point energy, I never mentioned temperature. That’s because zero-point energy is a zero-temperature effect — that is, it is a property of the system even when at zero temperature. My choice is appropriate for the universe, because any thermal effects are tiny compared to the calculation I’ve done for you.

      Let’s get an easy thing straight first. Take a solid object like the Earth, at zero temperature. If you take two such objects with the same mass but different density, then (a) they will generate the same gravitational pulls on any object far away [i.e. at sufficiently large distances, mass determines the gravitational acceleration] but (b) the gravity at the surface of the two objects will be different, because the object with greater density will have a smaller radius, and so the gravity at its surface will be larger. That’s true in Newton’s gravity, and Einstein’s gravity doesn’t change it.

      However, now imagine filling the entire universe with rock, or with some other substance. For this purpose, imagine the universe is infinite, which means that it has no central point — all points within it are equivalent. That means that the substance can’t collapse gravitationally. Why? A ball of material collapses toward its center, but there’s no center in this infinite universe, so where could it collapse to? Any part of the material is pulled to the left by an infinite amount of material and to the right by an equally infinite amount of material (and this is true in any direction) so the net gravitational pull on any one part of the material is zero.

      [The same would be true if the universe were finite but had no center. This is hard for non-math people to imagine, unfortunately; but a 1-dimensional example would be a line segment where the point at the left end is the same as the point at the right end, so you can travel to the right forever— when you reach the right end you discover you’re at the left end too, and so you can keep going. The universe can be just like this but in three dimensions.]

      In Newton’s gravity, that’s the end of the story. But not in Einstein’s. Einstein’s theory says that space (and time) will respond to the presence of the material, and the space itself will expand or contract. If the material is a gas, this the gas’s density can decrease or increase uniformly. If the material is a liquid or solid, its response to the growth or shrinkage of the space that it occupies can be quite complicated.

      Overall, it’s very easy to ask simple questions in general relativity only to discover that the answers are ambiguous and much more subtle than you realized. For example, what is the density of a black hole? Sounds like a simple question, but it’s completely ambiguous and even meaningless. (To define the density, you want to ask: how is the energy density of the black hole distributed right now? But “right now” has no unambiguous meaning.) Even if you ask “what is the energy density locally”, you find that is ambiguous. Identifying meaningful questions in general relativity is an advanced subject, and part of why defining a quantum version of gravity is very subtle. Because of these issues, I choose my questions carefully, hoping to avoid these ambiguities.

      Reply

    2. Thanks for the response, and I realize compressing a gas isothermally requires the removal of energy put into the gas by the compression. I was thinking more along the lines of a cylinder / piston arrangement. The gas is originally at some temperature, T1. I do work on the gas compressing it, while also removing energy during the compression. As such, after the compression, the gas is still at the original energy content associated with T1. The energy that was put in by the compression has been removed, so the gas itself has had no net energy added to it, but the energy associated with T1 is now in a more “dense” state. I read Dr.Strassler’s response, but thanks anyway.

      Reply

      1. Dr.Strassler :
        I realize compressing a gas isothermally requires the removal of energy put into the gas by the compression. I was thinking more along the lines of a cylinder / piston arrangement. The gas is originally at some temperature, T1. I do work on the gas compressing it, while also removing energy during the compression. As such, after the compression, the gas is still at the original energy content associated with T1. The energy that was put in by the compression has been removed, so the gas itself has had no net energy added to it, but the energy associated with T1 is now in a more “dense” state. In other words a higher pressure. Thank you for your in depth response.

        Reply

        1. Dr Strassler:
          Oops, meant to add this to the above, before I hit send.
          I was actually verifying my understanding of a response you gave to another poster:

          “In Einstein’s theory of gravity, high pressure gases feel more gravity than lower pressure gases”
          That was the origin of my original post /question concerning a compressed gas, at a higher pressure, but original temperature (same amount of moles & total energy content)
          That was the intent of the original question of my post.

          Reply

          1. In the non-relativistic limit (molecular speeds << the speed of light), the ideal gas law says p = n (k_B T), where n is the molecular number density and k_B T is proportional to the kinetic energy *per particle*, up to a numerical factor. Therefore p = (numerical factor) * kinetic energy density; you can’t compress the gas, leave the energy density the same, and change the pressure (or vice versa). Anything you do to the pressure affects the energy density in the same way — in the non-relativsitic limit.

            Moreover, in this limit, the kinetic energy is much less than the E=mc^2 energy stored in the particle masses, so p << total energy density for a gas of particles in non-relativistic motion.

            If the temperature becomes so high (k_B T ~ mc^2 for the molecules) that the particles move at speeds near c, then the kinetic energy dominates over the E=mc^2 energy. p = n (k_B T) is still true, but now it implies that p ~ total energy density, up to a numerical factor.

            So the effect I am referring to is independent of the one you were trying to imagine. It arises from corrections to the usual first-year-university physics formulas, due to the fact that Einstein’s relation between temperature, energy and motion is different from Newton’s, even though the ideal gas law is the same.

            Reply

      2. Cylinder/piston arrangement is a very good example. Even if you maintain the gas at a constant temperature keeping the internal energy of the gas constant, some of the applied work is stored as its potential energy, similar to a spring. Later you can extract that energy by releasing the piston and making useful work. If you keep the piston thermally isolated during the release, the gas will cool. This is how heat pumps work.

        Reply

  3. Dr.Strassler:
    That was a good read, helped clarify some points for me. Eagerly awaiting your book. This may sound very layman, but I would like to give it a shot. In Eisenstein gravity, it’s not just the magnitude of the energy, but the concentration (density) of the energy ( I realize there are other factors, like momentum, but I’m just detailing the energy part). For instance, in an ideal gas, the energy content is indicated by the temperature. If I was to compress a volume of gas, isothermally, the magnitude of the energy content would remain the same, the mass of the gas would be the same, but the same amount of energy, squeezed into a smaller area, would have greater gravity….correct?

    Reply

    1. Yeah, those news outlets don’t know what they’re talking about. It’s not really their fault, because it’s tricky to explain. It’s not actual gravity that’s being used; it’s an imaginary gravity, or gravitational mimicry by other forces, that allows you a method to study the very same energy-momentum tensor of the proton that you could study if you really did have strong enough gravity.

      What it’s similar to would be the following. Suppose there was no actual photon and no actual electric and magnetic forces — or suppose they existed but were almost too weak to measure. You might still be able to study the electric charge distribution of the proton, not with a real photon, but instead using a physical effect that, in a particular context, mimics a much stronger electric interaction than the one you actually have.

      What’s behind these articles is this: there is a perfectly ordinary electromagnetic process, known as deeply virtual Compton scattering (DVCS), from which you can extract the same information that you could obtain if you had much stronger gravity than you actually do. That’s why the diagrams at the top of the page that you cited do not contain any gravitons, or anything gravitational at all; it’s all electrons, photons and protons, for which gravitational effects are as small as always. The cleverness of the theorists behind it is in recognizing how to extract the same information that scattering off of gravitons would give you, even though you can’t actually do that.

      But all this tells you is where the energy, momentum, and other internal features of the proton are located. That’s what’s contained in the energy-momentum tensor. It tells you actually nothing about gravity itself — about how spacetime responds to that energy, momentum and so forth.

      I hope that’s clear; let me know if it fails to get the point across.

      Reply

      1. Thanks, another question. It’s generally stated that quantum corrections to GR become important near singularity hidden inside a black hole. Does it mean that even newly available gravitational wave signals and direct black hole observations still can’t probe truly quantum regime of gravity as they observe areas just outside the black hole horizon?

        Reply

        1. No, it is widely believed that we are nowhere near measuring anything obviously quantum about gravity. Collisions of black holes and the consequent creation of gravitational waves are just as classical as would be the collision of two large electrically charged spheres and the consequent creation of electromagnetic waves.

          It’s not so much the location as the nature of the measurement. There are measurements that one could make near a black hole horizon (or, indeed, anywhere) that would reveal gravity’s behavior in naively quantum regimes. But we can’t do those measurements. The sense in which the region near of high curvature near the putative singularity would, in principle, be a good place to look is that all physics at that location is extreme. But of course, it’s widely believed that we cannot measure anything behind the black hole’s horizon, including the region near the singularity.

          What I’ve just said is all mainstream views. People do sometimes suggest radical alternatives for how quantum gravitational effects might show up.

          Reply

          1. Sometimes it feels like particle physics is hitting a wall. No new effects at LHC, dark matter searches null results. What are best hopes for the next big breakthrough? Cosmological probes of the inflation, or neutrino physics?

            Reply

            1. This is too big a question for today. The short answer is that I don’t know; the long answer involves laying out all the issues in detail. Let’s talk about this at a later time when I put up a post that’s more directly relevant.

              Reply

          2. How is Leonard Susskind’s paper, Strings, Black Holes and Lorentz Contraction, seen today as a possible observational test of quantum gravitational effects?

            In the introduction he writes:

            “In particular the usual Lorentz contraction of particles must saturate when their momenta approach the Planck scale. In other words the physically measurable longitudinal size of a particle must tend to a constant and not decrease like its inverse momentum. Furthermore the transverse size of boosted objects must grow with momentum. These requirements would certainly seem unbelievable if it were not for one circumstance. They are found to be true for the propagation of relativistic strings.”

            I’m wondering if the signals at LIGO and future versions etc may observe effects of the Lorentz contraction of black holes as they collapse into one another in ways that may seem ‘impossible’ to measure today.

            Reply

            1. This is an advanced topic, and my sense is that you may not be interpreting it correctly. I have not written about it on this blog (though I have as a scientist); it’s not something one can understand without advanced quantum field theory. Moreover, the effect is true of elementary particles, not of anything macroscopic like the black holes that LIGO observes. In short, this is absolutely nowhere close to observability.

              Reply

        2. I think that’s a definite maybe.

          There isn’t a quantum theory of gravity, there are various ideas in that direction (or even in other directions) and some of them have potentially observable effects. This is covered in Section 5 of our draft paper to Living Reviews ( https://arxiv.org/abs/2312.02130 ).

          “There is consensus that trans-Planckian curvature scales are governed by an as of yet unknown quantum theory of gravity which modifies the core of a BH. However, quantum-gravity effects may affect the structure of BH spacetimes at much lower curvature scales and even structure outside the horizon.”

          That “structure outside the horizon” could be observable with the EHT, but would probably require its extension into space, such as by the Black Hole Explorer (formerly the EHE, now at https://www.blackholeexplorer.org/ )

          Reply

    2. No, I don’t thing so. This uses a mathematical analogy to gravity, through this from MTW

      “Any mass-less spin-2 field would give rise to a force indistinguishable from gravitation, because a mass-less spin-2 field would couple to the stress-energy tensor in the same way that gravitational interactions do.”

      to do calculations with the strong force (QCD). If the calculations didn’t match observations it would be a test, not of gravity, but of QCD.

      Reply

      1. Understanding the problem from a different perspective always reveals the path of minimum effort to its solution. Take some time to read the article for the perspective to become clear. I will also be giving an online talk on this paper this coming Thursday at 8am EST to a specialist audience who may have questions.

        Reply

        1. Since I published today’s webpage, I have received three proposals for scientifically sophsticated solutions to the cosmological constant problem — i.e., by people who do know how to write and understand equations. All of them claim, of course, to be cogent. But they contradict each other, so at least two of them are wrong. I’m sure each author has a different opinion on the validity of the other papers.

          This is a hard problem, and there have been a slew of proposed solutions to it; you’re not the first and you won’t probably be the last. Even the cogent solutions usually either have an error or simply don’t agree with some aspect of existing data.

          But if you’re right, I’m sure it will become clear eventually.

          Reply

  6. Nice, but I don’t read why ‘in a box’ is also relevant when the length of the box is taken to infinity. Standing waves have sizes that are fractions of the box size. But when taken to cosmic scales? No wave interference there, just traveling waves. I’m sure you considered this but left it out for clarity. But it bugs me.

    Reply

    1. Yes, it’s absolutely a fair question. I did finesse this point, for clarity, although I knew some readers would wonder about it. Maybe I should add an aside about it in the text.

      Notice that the energy-density doesn’t depend on the size of the box, so we can take the box to infinite size and still get the same energy density. As another sign of this, notice that the dominant contribution to the zero-point energy is from the standing waves that have the smallest spacing, and care the least about the size of the box. They are affected by the small-scale structure of the universe, not its large-scale structure. It’s the waves with the smallest frequencies that care most about the overall size of the box.

      You can do the same calculation for traveling waves in an infinite box. You’ll then have to deal with some infinities that I didn’t have to, because the total zero-point energy of the universe will be infinite. (In fact, the way most people deal with it is to take a box with periodic boundary conditions — a three-dimensional torus — which does indeed have traveling waves, and then take its size to infinity.) But if you do it right, you’ll find the same zero-point energy density that I did. Of course, that calculation would be harder to follow. I think the waves-in-a-large-box calculation is easiest for a person with just pre-university math to keep track of, even though it does leave this lingering question.

      Reply

Leave a Reply

Search

Recent Posts

Buy The Book

A decay of a Higgs boson, as reconstructed by the CMS experiment at the LHC

Order Waves In An Impossible Sea

Harvard Book Store
Book Passage
Powell's Books
Elliot Bay Book Company
Vroman's Bookstore
Amazon
Barnes & Noble