Matt Strassler 11/14/11
One of the most confusing things about the Big Bang is that it involves an expanding universe. Any reasonable person, hearing about the Big Bang, will imagine something that he or she has seen expanding: a cloud of smoke exploding outward, or a balloon expanding as it is filled with air. This is very natural. And having imagined this, the reasonable person will ask, “But what is the universe expanding into?”
This reasonable though seemingly paradoxical question is simply the wrong question. It is a consequence of having imagined the wrong thing. My goal here is to set your thinking straight.
Let’s go back and look at Figure 3 from the Worlds of 1 Spatial Dimension article, the relevant part of which is shown at the top of Figure 1 below. Notice there are two very different representations of the aeolian line (the dimension of possible wind-directions, which include the directions north, south-east, west-north-west, etc.) One representation is as a line segment whose left end is the same as its right end. The other is as a loop drawn in a plane. Now wait a second, you might ask. These look different. The loop surrounds an area, so it has an inside and an outside. The line segment doesn’t seem to have this. So how can these represent the same thing?
Fig. 1: (Top) A circle can be represented as a line segment with its two ends the same point (marked in red) or by a loop drawn in a plane (where the open red dot is the same point as the red dots on the segment.) From the line segment representation it is easy to see that a circle has no inside and no outside. (Bottom) A torus can be represented as a rectangle with its upper and lower edges the same (marked in red) and its left and right edges the same (marked in blue.) The torus can also be represented as the surface of a tire, or doughnut. To see these two representations are the same, join the top and bottom to form a cylinder, then the two ends to form the tire. Though the tire appears to have an interior, the rectangle representation makes clear that a torus does not intrinsically have an inside or an outside. The joining seams are shown as dotted lines.
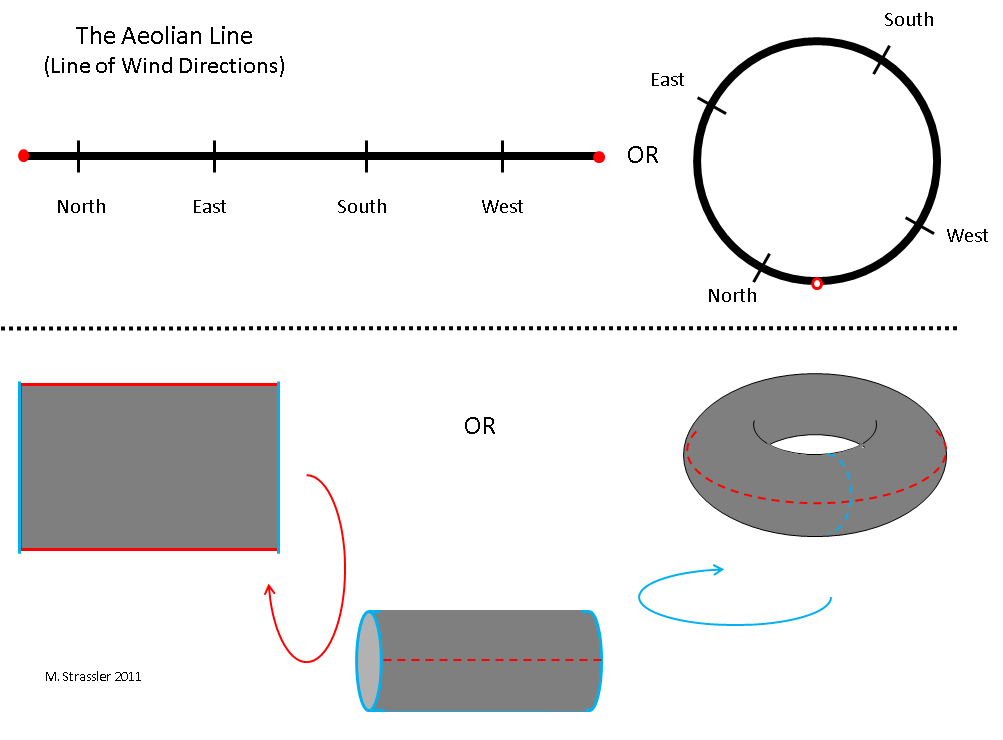
Ah! This is indeed a crucial question, and the answer is vital to understanding spaces. The two representations — the loop, and the line-segment with its two ends matched — do represent the same one-dimensional aeolian line. The area that the loop surrounds is a property of the representation that we have chosen, not a property of the aeolian line itself! We must never confuse properties of pictures that we use in visualizing a space with properties of the space itself!!! That is very easy to do, but it is crucial not to do it.
As another example, it looks as though the doughnut (torus) drawn in Figure 1 has an inside and an outside. But it doesn’t. Just as a circle can be represented as a line segment with the left end and right end being the same point, a torus can be represented as a rectangle whose top and bottom edges are the same and whose left and right edges are the same. (To see that this is true, take a piece of paper. Attach the top edge to the bottom edge. You will now have a cylinder. Now you have to use your imagination to bend the left and right ends of the cylinder around so that they touch: but you will quickly see this will give you a torus.) There’s no inside or outside for our rectangle with matched edges, so there’s no inside or outside for a cylinder or for a torus. In other words, what is essential about a space is what you would learn about it if you traveled within it. To see the circle has an outside or an inside, you would have to travel across it: but if your circle is the aeolian line, that’s impossible. You cannot ask the wind to cut across the circle from north to south-east! It can only go around the circle, via east or via west and south. The only thing intrinsic to the aeolian line is the line itself!
And similarly, you cannot ask the tight-rope walker, from Figure 6 of the Worlds of 1 Spatial Dimension article, to cross from one side of the circular high-wire to the other. The only safe motion for the walker is to go around the circle one way or the other. So there is no way for the wind, or the walker, to find out whether there is or isn’t an interior or exterior to the circle.
This conceptual point is actually really important in understanding the expanding universe. If you are like most people, you’ve probably wondered (as I did when I was young), “What is it expanding into?” Well, in asking this question you are making the same mistake as for the circle: you are confusing something expanding with a representationof something expanding.
Fig. 2: Fig. 2: We are used to thinking about an inflating balloon expanding within three-dimensional space. It seems to have an interior and an exterior. But this just is a representation of an expanding sphere. An ant on the sphere could just as well represent it as a disk whose outer edge is a single point (as in a map of the globe with the north pole at center and the south pole at the edge.) It is then clear that it has no inside or outside, and does not expand "into" anything. It just expands, period, and this is evident to the ant from the fact that the distance between any two locations (such as the yellow and blue points shown) increases.
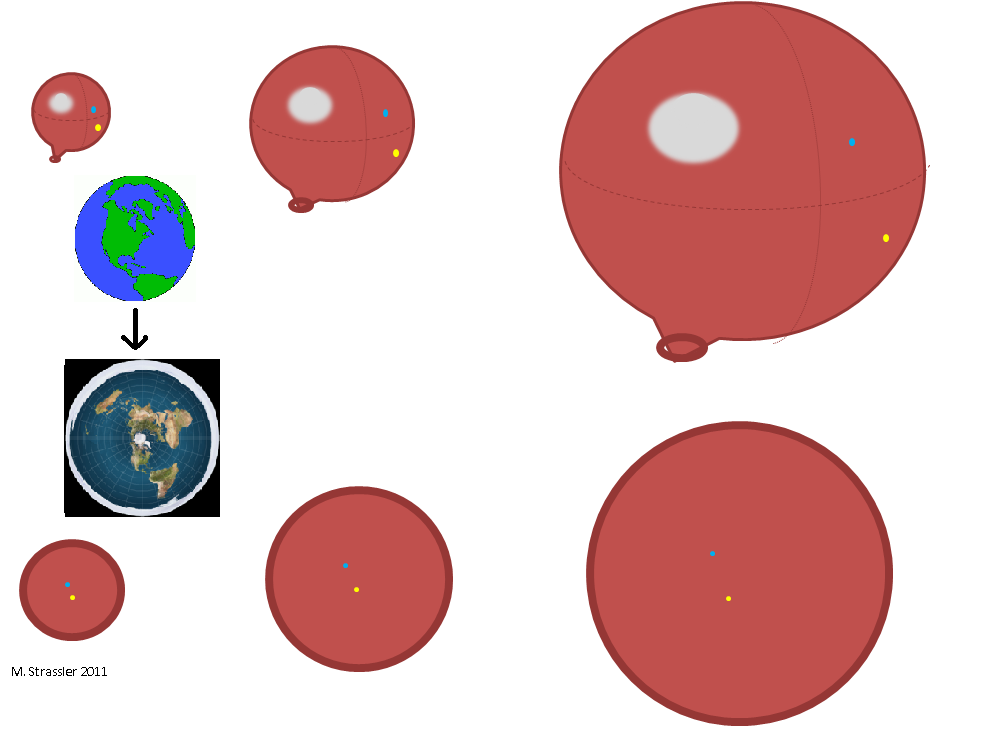
For example, you might imagine an expanding balloon. A balloon looks to us as though it is growing into the larger three-dimensional space in which it sits. But if you were an ant on the balloon, you would not know anything about some rumored interior or exterior; all you would know is that the space on which you can walk has become larger. In fact you might (as an ant cartographer) represent the space as a disk whose edge is all one point (for instance, the point where the balloon is being inflated). You wouldn’t think about inside and outside; all you’d know is that the distance between the yellow and blue points (and indeed between all pairs of points on the balloon) is growing.
Another two-dimensional space is the surface of the earth itself. Suppose you woke up one morning and the earth’s surface had doubled in size. You wouldn’t know whether the earth looked different to an observer out in space, or whether the diameter of the earth had grown. All you’d know is that when you walked to work or drove to get groceries it would take longer than it used to.
That the interior or exterior of the balloon is a property of the representation of an expanding space, and not of the space itself, is more obvious in the case of an infinite plane. It is possible for an infinite plane to expand, though it is not expanding into anything. It fills exactly the same space after it expands as before; but the distances between objects on the space (for instance, the dots shown in the figure) has grown. The plane is intrinsically growing in size; it isn’t inside a larger space, and so it obviously does not — cannot meaningfully — expand into that larger space. It just expands, period.
Fig. 3: An infinite plane can expand. It doesn't expand into anything; but the distance between any two points, including between any pair of colored points drawn above, grows as the plane expands.
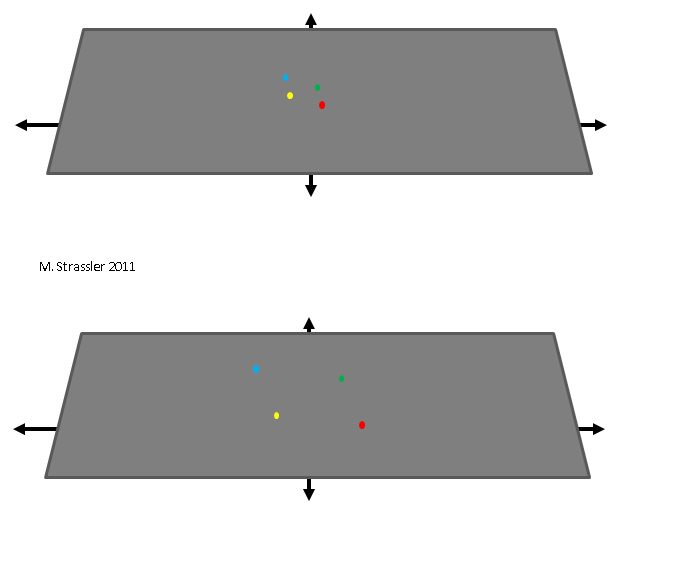
So it is with the universe. Like the plane just described, the space of the universe simply expands. There’s no way to see this from the outside; there is no outside. But you can tell the universe is expanding from within the plane itself: the distance between all of the big objects in the universe (in particular, between the galaxies, the universe’s great cities of stars) grows and grows as the universe expands. Over time, it takes longer and longer to go from one big galaxy to the next. That’s what the Big Bang did: it took small regions of space and made them huge. It wasn’t an explosion; it’s not like a bomb going off. It’s an expansion of space itself.
Prof. Matt Strassler : “In other words, what is essential about a space is what you would learn about it if you traveled within it.”
Savas Dimopoulos: “Here’s an analogy to understand this: imagine that our universe is a two-dimensional pool table, which you look down on from the third spatial dimension. When the billiard balls collide on the table, they scatter into new trajectories across the surface. But we also hear the click of sound as they impact: that’s collision energy being radiated into a third dimension above and beyond the surface. In this picture, the billiard balls are like protons and neutrons, and the sound wave behaves like the graviton. ” – http://archive.sciencewatch.com/may-june2001/sw_may-june2001_page4.htm
Finding and understanding a inside\outside has been very difficult. Seen an example as a cookie being baked and with chocolate chips ……the distances between these chips are expanding…..as the universe. Okay then, Dark matter or dark energy? There is then an abstract notion about the distances? Greene may of call this a liminocentric view in the relationship of ourselves with the world? It is the difficulty of explaining our views in relation to what is to come in looking at the sphere?
http://4.bp.blogspot.com/_cldxKGOzgeM/R7EQnddHDQI/AAAAAAAAAuk/-4sKU3816wI/s320/inside1.jpg
“This is a torus (like a doughnut) on which several circles are located. Unlike on a Euclidean plane, on this surface it is impossible to determine which circle is inside of which, since if you go from the black circle to the blue, to the red, and to the grey, you can continuously come back to the initial black, and likewise if you go from the black to the grey, to the red, and to the blue, you can also come back to the black.” – Conventionality of Topological Structure – http://www.bun.kyoto-u.ac.jp/~suchii/topology.html
best,
“If conceived as a series of ever-wider experiential contexts, nested one within the other like a set of Chinese boxes, consciousness can be thought of as wrapping back around on itself in such a way that the outermost ‘context’ is indistinguishable from the innermost ‘content’ – a structure for which we coined the term ‘liminocentric’.”
Hard concept to grasp professor. So if the universe is not expanding “into” anything how come in the pass we were expecting it to “bounce back” from “somewhere”?
The “bounceback” refers to a time when expansion stops and contraction starts. This may or may not happen.
As with expansion, the bounceback is not “from” somewhere. In the balloon analagy, you are not outside the balloon looking in, you are part of the balloon itself
I’ve often wondered about this thought experiment…
Presumably, the distance between the particles (speaking loosely here) making up the person or instrument measuring this distance also increases in this scenario? But if that is the case, how would any measured distances change?
If I am the one measuring distances for example, and the spaces between my atoms increases by the same proportion as those in the space I’m observing (since, after all, the colored dots in your diagram include those making up my body), then my legs and hence my steps would also be bigger, making it hard to see how I would notice the change.
If I get a bit more savvy and try to use a pulse of light to measure the distances, then doesn’t the distance between successive crests or troughs of the EM wave also increase, just like my step sizes, compensating for the expansion in the underlying space?
Good question. The point is that space is expanding relative to the size of a person or instrument.
What sets the size of a person or instrument? Well, really what it is important to all ordinary objects is the size of an atom. An atom is an object built by trapping electrons (using electromagnetic forces) around an atomic nucleus. The size of an atom is set by the mass of the electron, the strength of the electromagnetic force, Planck’s constant and the speed of light. None of these is changing while the universe is expanding — so as the space within the universe expands, atoms do not. Similarly, hydrogen molecules, proteins, DNA, crystals — all of these have sizes that are set by the masses of the objects that make them up and the strengths of the forces that hold them together.
The expansion of the universe effectively tries to drive everything apart — and everything that is not attached to something else will find itself further apart from everything else that it is not attached to. But once attachments occur — strong-nuclear ones that hold atomic nuclei together, electromagnetic ones that hold atoms and molecules and instruments and humans together, and also gravitational ones that bind stars and gas together into galaxies — the expanding universe is not able to break those attachments. And that is why there are objects of a fixed and definite size inside a universe that on average is expanding uniformly.
Would it be possible to come up with a set of changes to the masses of particles, the speed of light and other constants that would be indistinguishable from an expanding universe? Matter getting smaller rather than space getting bigger. I expect that there’s a flaw somewhere but I’d be interested in your thoughts.
You can actually do that if you want. You can rewrite all the equations so that instead of space expanding and other things remaining the same size, everything else is shrinking and space is staying put. But you haven’t changed the results of human experiments, which will be shrinking along with everything else. So we have two entirely equivalent descriptions of the world, one with an expanding universe and one with shrinking protons, atoms, stars, planets, and changing masses for all the particles — and it is up to you to choose the one you prefer. Here’s where Occam’s razor makes an appearance. There is no harm, and much benefit, in choosing the simpler one, so apply Occam’s razor and select the version of events with an expanding universe… remembering, always, that this was a choice. We can also put the earth at the center of the solar system, if we are willing to make all our equations for the laws of nature much more complicated; but Occam recommends “no”.
The existence of multiple equivalent descriptions of the world is something scientists are quite used to. I stress the word “equivalent”; no experiment could distinguish them. There is much arbitrariness in our scientific choices. But it is fine to be arbitrary, as long as you remember what your choices were and why you made them. Sometimes Occam guides our choices; sometimes there are two comparably simple descriptions of a phenomenon, and then Occam doesn’t vote. In fact scientists often keep multiple descriptions around, since one may be useful in one context and another in a different context.
But for the universe, it is pretty clear that it is simpler to think of space expanding and atoms and protons as of fixed size.
P.S. Further to my question above, when people talk about this expansion, in relation to the big bang, are they talking about the expansion of *space* or are they talking about the expansion of *spacetime*?
If it refers to space, then I’ve never understood how they separate out a particular choice of space from the assumed spacetime of general relativity.
If it refers to spacetime, then the diagrams above are even more misleading to our intuition because the geometry is totally different than the one our brain is using to process these pictures.
If an infinite plane can expand does that not define it as less than infinite to begin with?
No. Infinity can expand, even though it is infinite before it expands and infinite afterward.
Take the numbers 1,2,3,4,5,…. going on to infinity. Double them: 2,4,6,8,10,… going on to infinity. I can now insert new integers between them: 1,3,5,7,9,… In other words, by doubling the integers (an infinite set) I have found room for new integers that wasn’t there before.
Conversely, nothing finite can expand to become infinite. Take any set of integers: 1,2,3,4…, 1000. Double them, and insert integers between. Now you have a larger set of integers: 1,2,3,4…,2000. But no matter how many times you do this, you will still have a finite set of integers.
Hi, Matt – This post inspires a couple of questions that have nagged at me over the years –
My mental picture of the universe is of an infinite volume that is everywhere peppered with galaxies in pretty much the same way that our surrounding few billion light years are. Is that the right model, or are all bets off beyond the observable horizon? Assuming it is thought to be the right model, I have talked to (and even corrected) people who instead imagined a finite ball of galaxies expanding into otherwise empty space. But is it actually known that that model is wrong? You can certainly imagine an expanding ball of galaxies a few hundred billion light years across, with our observable universe as a little ball buried somewhere deep inside. To us, that would look more or less the same as the infinitely-many-galaxies model. Are there non-Occam grounds to reject the second model? I suppose if it the second model were true it ought to generate an anisotropy in the CMB, but what if the giant ball were big enough we couldn’t detect it? There might also be strong theoretical grounds to reject such a wildly inhomogeneous early universe. Are there?
In the same vein, some of the lay explanations for the anthropic-principle arguments for how we ended up with physical constants that permit life seem to suggest that these “other universes” are actually just really large scale inhomogeneities in a single infinite space time continuum. Do I understand that right? Or do you know? I do realize you’re not a cosmologist.
Mark, your mental picture is certainly closer to correct than the “finite ball of galaxies in empty space” picture, which is quite wrong. However, once we go outside the observable part of the universe into the regions beyond, your guess is as good as mine.
The theory of inflation predicts that some part of the universe beyond what we can see will be similar to the part we can see, but the size of that part isn’t predicted, and anyway inflation theory is not well-enough tested for us to rely upon it yet. We certainly have no idea what happens at the edge of that region, and we see no signs of any edge in the part of the universe that we can observe.
Many variants of inflation predict the universe on the larger scales (far beyond what we can see) is a very complicated place and that most of it (but define “most”! that will occupy you for a while) is probably very different from the part that we can see. If in fact the universe is huge beyond imagining and very inhomogeneous, arguments using an “anthropic-principle” (or better, a “selection-principle”) do say that just as we live on a rock in a universe that is mostly not rock, we may live in a rather unusual part of the universe because, hey, that’s the only place we can live. So the answer to your last paragraph is “yes, you understand that right”. One very, very big universe, with lots of different regions, only a few of which are habitable.
I’ve read a little bit about the the inflation model, but I have a hard time understanding how the model can be thoroughly tested. Since we are “stuck” in our observable universe, it seems difficult to gather enough evidence for or against various inflationary models.
I imagine this is similar to our galaxy many billions of years in the future – at a time when space is expanding so fast that no other galaxies are observable. Inhabitants of that time period would look out into space and incorrectly assume that our galaxy is the entire universe, and that the universe is static and infinite.
Perhaps I just do not have enough technical knowledge to understand the ramifications of inflation that can be verified by experiment.
It’s not obvious how this is done. It’s quite a sophisticated subject!
Certainly here are limits to what one can test, clearly, for the reasons you stated; you can’t actually see what’s outside our horizon.
However, it turns out that inflation makes a prediction that quantum fluctuations in the field that drives inflation (called the “inflaton field” — this is the field that provides the temporary “dark energy” or more accurately “cosmological energy density” that causes the inflation) lead directly to the density of the universe not exactly constant, and those regions of slightly larger density collapse and form the galaxies and clusters of galaxies we see today. The details of inflation, as the inflationary period comes to a close, determine precisely what are the average size of and distribution of those slightly more or less dense regions. A lot of details about these regions of higher and lower density can be determined by very precise measurements of the leftover heat from the Big Bang (the cosmic microwave background) and from other measurements that are sensitive to how dark matter and galaxies are distributed. These measurements can be used then to rule out various models of how inflation occurred in favor of others.
Interesting, thanks for the reply. Sounds like I should read more of the summaries from WMAP. I understand that the measured anisotropy of the CMB was used to calculate the geometry of spacetime, but I did not realize it also was used to check predictions made by the inflation model(s).
By coincidence, I was recently having a discussion/argument with someone who was using “The God of the Gaps” to explain the matter/antimatter asymmetry of the Hadron Epoch. He had heard (probably on the internet), that “the laws of physics were suspended a millisecond after the Big Bang” and that resulted in all visible matter. The conclusion was that God must be responsible.
I was trying to explain in a general sense why God of the Gaps does neither science nor religion any favors, quoting people ike Georges Lemaitre. However, I realized that I did not even know the leading hypotheses as to why the asymmetry may have happened, let alone how we might test our theories.
One last comment… this dicussion and others I’ve had with non-science educated adults have made me realize something you and your colleague may find important. The average adult has no idea how cutting-edge physics theories are tested! They think it is like “philosophy,” by definition untestable, which places it on the same grounds as religion. This view is likely something perpetuated by the media and/or pop science. They know generally what a particle collider is, but they have absolutely no idea what it actually does and why that is significant! Nor do they know about the stunning science being done by spacecraft like WMAP, Planck, JWST (hopefully), etc.
Hello Prof. Strassler,
I found this link very very instructive:
http://www.astro.ucla.edu/~wright/infpoint.html
and this one also:
http://www.astro.ucla.edu/~wright/photons_outrun.html
Going backward in time (reversing time) I see more clearly now that we can understand the universe untill its density becomes so high that our laws of physics break down but that the universe was (probably) already infinite at that point in time. Is that a correct view?
The expanding balloon concept of the universe with the surface representing 3 dimensional space makes a lot of sense to me. The surface is infinite in so much as it is a seamless surface. One could travel along it’s surface forever. One could eventually come back to the starting spot unless there was a speed limit (c) equal to the rate of the expanding surface area. Could the ever increasing surface area represent entropy? Could it also be analogous that the 3 dimensional surface is expanding into a 4th dimension of time?
I haven’t seen you reply to Derek’s question regarding whether it’s space or spacetime that’s expanding, but let me follow up on it. Similar to Derek’s reasoning, I’m assuming that it’s spacetime that expands. If that’s true, then can we actually determine that our space has expanded my measuring the time it takes to go somewhere, as in your example about detecting the hypothetical expansion of the earth’s surface but the increase in the time it takes to walk to work? If our time dimension has also expanded, wouldn’t the time sensors (our wristwatch or the neurons in whatever part of our brain lets us imagine the passing of time) also slow down, giving us the same perceived time interval for the walk to work?
Sorry, occasionally I miss a comment.
Space is expanding, not spacetime; to expand means to increase in size as time goes by, and that’s clearly not something that spacetime (which includes time and cannot, therefore, change over time) can do.
To say that a space is expanding requires that you can look at the space at a given time and ask whether it is expanding or not. For most spacetimes, you cannot even ask this question. Only for those spacetimes for which there exist observers from whose point of view space more or less maintains its shape over time, only changing its size, can this question even be asked. It happens that the visible part of the universe satisfies this criterion to a good approximation. The spacetime of the universe as a whole, if we could ever learn about its parts that lie far beyond the part that we can see, may well not permit this question.
I understand that the Universe is essentially spatially flat. But, growing up, this was far from a known fact, and curved geometries, both closed and open, were (and, to a lesser extent, still are) discussed. There is (at least
one point I was never clear on, however, in terms of curved universes.
We live in a universe of 3 spatial dimensions (absent the extra dimensions of string theory). If the 3-D universe was curved (say, in a Riemannian fashion that made it a closed universe), is that curvature *within* the 3-D space, or does that curvature imply that there is a 4th dimension that the space is curved through (in much the same manner that a sphere is a 2-D surface curved through a 3rd dimension). If the latter, then I suppose the next natural question is how that 4th physical dimension would relate to string theory’s extra dimensions.
Or is it the case that curvature within the 3-D space and curvature through a 4th dimension are somehow mathematically equivalent?
One could, of course, ask the same questions about the curvature of space around a massive body due to gravitation.
The key thing you need to learn is that you can tell that a sphere is curved WITHOUT LEAVING THE SPHERE. Two parallel lines will converge. You can go straight, keep walking and walking, and one day you’ll find you come back to where you started.
It is not the case that a two dimensional sphere, in order to be a sphere, must be embedded in three dimensional space.
Similarly, the universe’s three-dimensional shape might (though we have no evidence for this) be in the shape of a three-dimensional sphere. If it is, THERE IS NO NEED TO IMAGINE PUTTING THIS SPHERE INSIDE OF FOUR DIMENSIONS OF SPACE. You can have a three-dimensional sphere without putting it inside of anything. You just check the parallel lines. You see whether you can go all the way round.
So no, we do not imagine that our three-dimensional universe, if curved, sits inside of a larger space with more dimensions.
For the same reason, the expanding universe is not expanding INTO anything. It’s just getting bigger, and you can tell that without ever going “outside”; there is no outside to go to. If it is in the shape of a sphere, the statement that it is expanding just means that you will find it takes longer and longer before your walk brings you back to where you started.
“It is not the case that a two dimensional sphere, in order to be a sphere, must be embedded in three dimensional space.”
Thank you; I’ve *never* seen that fact mentioned before *anywhere*. I’ve read a number of books, pitched at levels from elementary to advanced, that talk about the open/closed/flat geometries, and none of them bother to mention this simple fact. Actually, they leave quite the opposite impression, with their “rubber sheet” illustrations of curved 2-D spaces.
I am Enlightened.
And hearing this, I am Gratified.
I have seen it said elsewhere, but it is hard to say it clearly. I’m glad my way of phrasing it spoke to you.
Dr. Strassler wrote: “THERE IS NO NEED TO IMAGINE PUTTING THIS SPHERE INSIDE OF FOUR DIMENSIONS OF SPACE.”
Quite by accident, I stumbled across what was undoubtedly stuck in the back of my mind about this. I was watching a bit of random Carl Sagan in “Cosmos” the other day, wherein he explicitly stated that the Universe may have the shape of a three-dimensional sphere curved through a fourth dimension of space. Don’t get me wrong; I quite take your point that the Universe is not expanding into anything; I’ve made that point a number of times to my own audiences. But I wonder whether the two cases (curved through a higher dimension vs. intrinsically curved) are mathematically distinguishable?
He may have said that, but this is clearly not what he meant. I don’t think he meant we should drop Einstein’s notion of the relation between space-time and gravity. If you accept that notion, then, if we lived on a three dimensional sphere inside four dimensions, gravity would have a 1/r^3 law, not the 1/r^2 that we’re used to. (Similarly, if you imagine that we lived on a two-dimensional sphere inside a three dimensional space, the gravitational force law between the sun and the earth would be the three-dimensional force law of 1/r^2, not the 1/r force law you would expect in two dimensions.)
When people talk about the universe being a three-dimensional sphere, they specifically imply there is no fourth dimension of space in which this sphere is embedded. The point is that you can tell the three-dimensional part of the universe is a sphere just by following parallel lines INSIDE the three dimensions and seeing how they diverge and converge and whether they return to a starting point.
By contrast, you can tell the universe is embedded inside MORE space dimensions either by moving off the three-dimensions into the extra ones (which may or may not be practically feasible) or by sending something out into the extra dimensions — such as gravitational fields. The ability of gravitational fields to enter large and flat extra dimensions causes the gravitational force law to be diluted compared to the three-dimensional expectation.
(Sorry for the delay in responding; I forgot where this conversation was on your site, and it took me a while to find it!)
Since I was so informed by your statement that the Universe is NOT embedded in a fourth dimension, let me ask another simplistic question. The last two paragraphs of your article talk about an infinite plane; but I’m wondering if it is possible for the Universe to be flat (as it apparently is), *finite*, and unbounded.
Actually, your article doesn’t mention boundedness, so I hope I’m not confused by the concept. My understanding is that the surface of a 2-D sphere is finite (obviously) but unbounded, while a 2-D hemisphere (for lack of a better example) is finite but bounded at the equator.
(P. S.: I see that you’re considering whether this web site has a future. I want to thank you for everything I’ve learned from this (which has been considerable). Personally, I was looking forward to such eventual topics as electron orbitals, the weak nuclear force, (or, for that matter, the strong nuclear force, which I thought I understood a bit when it was pi mesons and don’t understand at all any more given quark confinement), and what the Pauli exclusion principle means in the context of the entire volume of a neutron star. Whatever you decide, thanks for what you’ve done so far.)
There are definitely manifolds that are flat and unbounded. If you remember the video game Asteroids, where you could go off one edge of the screen and return from another, that was an example of a geometrically flat but unbounded universe. Topologically, that shape is a torus, and to embed it in 3-space it would have to have curvature, like you see with the boundary of a doughnut. But intrinsically it can definitely be flat. People have tried to see evidence in distant sky surveys that would indicate some more interesting topology like that — a guy named Jeff Weeks was one person suggesting that kind of research a while back. But I have the impression the smart money is on infinite-and-unbounded. And I’m not a cosmologist, just a former mathematician, so take what I say with that much of a grain of salt.
Mark, thanks for the reply.
“There are definitely manifolds that are flat and unbounded.” You left off explicit mention of whether a 3-D manifold could be flat, unbounded, and *finite*. Your example is 2-D, so I am left looking for a definitive statement on whether 3-D manifolds can have all 3 properties simultaneously. I’m also aware that a huge radius of curvature can cause the manifold to appear *locally* flat, so I’m also interested in distinguishing that case from a globally-flat case. Thanks for any insight you can provide.
Well, the n-dimensional generalization of the “flat torus” is always flat, so there certainly is at least one flat, unbounded, finite manifold in every dimension. In the context of differential geometry and topology, unbounded finite manifolds are called “closed manifolds”. And I’m thinking these are the only examples, but I’ve really gotten rusty on this. But anyway, the answer is Yes: there is a 3-D manifold that has all three properties. Whether such a manifold is a plausible model for the universe “at any given time” is something a cosmologist, or at least a physicist, would have to answer. But I do think you would be really interested in the book The Shape of Space, by Jeffrey Weeks.
Thanks again, Mark. The Weeks book you recommended is on my list …
(I have a BS in math, myself, but it was a long time ago and I didn’t go the topology direction. My biggest regret is that I didn’t get into tensor calculus …)
When I read about the universe at the beginning of the Big Bang, it is often referred to as a single point that everything came from.
Does that mean it was a purely zero-dimensional thing? If so, did the 3+ dimensions we live in somehow unfold from it? How does that happen? How can dimensions be created?
Thanks for this article. It should have been the first on my list to read. Still I’m confused with words such as hyperspace, multiverse, parallel universes, and alternate realities. I understand to some basic extent the differences between ie., alternate reality and multiverse.