Matt Strassler [February 25, 2013]

The nucleus of an atom forms its tiny core, with a radius 10,000 to 100,000 smaller than that of the atom itself. Each nucleus contains a certain number (which we’ll call “Z”) of protons and a certain number (which we’ll call “N”) of neutrons, clumped together into a ball not much larger than the protons and neutrons themselves. Note that protons and neutrons are often collectively called “nucleons”, and Z+N is often called “A”, the total number of nucleons in a nucleus. [Recall that Z, called the “atomic number”, is also the number of electrons in the atom.]
The typical cartoon drawing of an atom (Figure 1) greatly exaggerates the size of the nucleus, but it does represent the nucleus more or less properly as a loosely combined cluster of protons and neutrons.
The Contents of a Nucleus
How do we know what a nucleus contains? These tiny objects are (and were, historically) simple to characterize because of three facts of nature.
1. a proton and a neutron differ in mass by only about one part in a thousand, so if we’re not being too precise, we can say that all nucleons have essentially the same mass, which we’ll call the nucleon mass, mnucleon;
- mproton ≈ mneutron ≈ mnucleon
(where the “≈” symbol means “is approximately equal to”).
2. the amount of energy required to keep the protons and neutrons together in the nucleus is relatively small, only about one part in a thousand of the mass-energy (E=mc² energy) of the protons and neutrons, so the mass of a nucleus is almost equal to the sum of the masses of its nucleons;
- Mnucleus ≈ (Z+N) × mnucleon
3. an electron’s mass is only 1/1835 as big as a proton’s — so an atom’s mass is almost entirely in its nucleus;
- Matom ≈ Mnucleus
[Implicitly there’s an equally important fourth fact: all atoms of a particular isotope of a particular element are identical, as are all of their electrons, their protons, and their neutrons.]
Since the most common isotope of hydrogen has one electron and one proton,
- Mhydrogen ≈ mproton ≈ mnucleon
the mass Matom of an atom of a particular isotope is, simply Z+N times the mass of a hydrogen atom,
- Matom ≈ Mnucleus ≈ (Z+N) × mnucleon ≈ (Z+N) × Mhydrogen
where these equations are accurate to about 0.1%.
Meanwhile, since neutrons are electrically neutral, the electric charge Qnucleus on a nucleus is just the number of protons times the electric charge (called “e”) of a proton
- Qnucleus = Z × Qproton = Z × e
Unlike the previous equations, this equation is exact, with no corrections.
Summarizing:
- Z = Qnucleus / e
- A = Z + N ≈ Matom / Mhydrogen
These equations are illustrated in Figure 2.
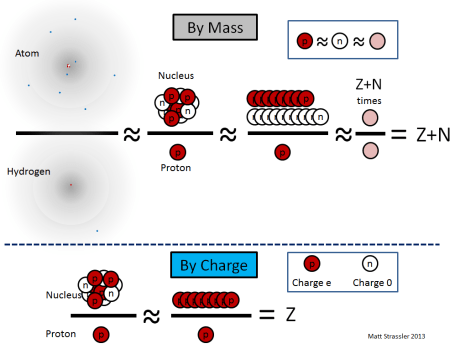
Experimentally, using discoveries of the late decades of the 19th century and the early decades of the 20th, physicists knew how to measure both of the quantities in red: the charge of a nucleus relative to e, and the mass of any atom relative to that of hydrogen. [Here’s one way (article coming soon) to do this and use it to confirm the structure of atoms and their nuclei, in case you’d like to know.] So these quantities were known by the 1910s. However, they were not interpreted properly until 1932, when the neutron (the idea of which had been suggested by Ernest Rutherford in 1920) was identified as an independent particle, by James Chadwick. But once it was understood that neutrons existed, and that the mass of a neutron was almost the same as that of a proton, it instantly became clear how to interpret Z and N as the numbers of protons and neutrons. [It also immediately raised a new puzzle: why do protons and neutrons have almost the same mass? We’ll return to this question in later articles.]
Honestly, physicists of that time period were very lucky, from the scientific point of view, that things were so easy to figure out. The patterns of masses and charges are so simple that most lingering confusions were quickly eliminated once the neutron was discovered. If any one of the four facts of nature I listed hadn’t been true, then it might have taken a long time to work out what was going on inside atoms and their nuclei.

Unfortunately, in other ways it would have been much better if things were more complicated. The timing of this scientific breakthrough could hardly have been worse. The discovery of the neutron and the understanding of the structure of nuclei coincided with the international economic crisis often called the Great Depression, and with the rise of several authoritarian and expansionist governments in Europe and Asia. A race among leading scientific countries to understand and obtain energy and weapons from nuclei quickly began; reactors generating nuclear power were obtained within a mere ten years, and within thirteen, nuclear explosives. Today we live with the consequences.
How Do We Know Nuclei are Small?
It’s one thing to convince ourselves that a particular nucleus of a particular isotope contains Z protons and N neutrons; it’s another altogether to convince ourselves that nuclei are tiny and that the protons and neutrons, rather than being crushed together into a pulp or stirred into a stew, more or less retain their integrity, as the cartoon nucleus suggests. How can we confirm these things?
I’ve mentioned before that atoms are mostly empty. There’s an easy way to see this. Think about a piece of aluminum foil; you can’t see through it. Since it is opaque, you might think the atoms of the aluminum are
- so large that there are no gaps between them, and
- so dense, thick and solid that there’s no way for light to sneak through.
Well, you’d be right about there being no gaps; in a solid there’s hardly any space between one atom and the next. You can see this in the pictures of atoms obtained using special microscopes; the atoms are like little spheres (their edges being the edges of their electron clouds), and they are pretty tightly packed together. But you’d be wrong about atoms being impenetrable.

If atoms were impenetrable, then nothing could get through the aluminum foil… not visible light photons, not X-ray photons, not electrons, not protons, not atomic nuclei. Anything you aimed at the foil would get stuck in the foil or bounce off, just the way a thrown object has to bounce off or stick to a plaster wall (Figure 3). But in fact, high-energy electrons can easily go through a piece of aluminum foil; so can X-ray photons, high-energy protons, high-energy neutrons, high-energy nuclei, and so on. The electrons and the other particles — almost all of them, to be precise — can go through the material without losing any energy or momentum in a collision with something inside one of the atoms. Only a very small fraction of them will hit an atomic nucleus or an electron head on, in which case they may lose a lot of their initial motion-energy. But the majority of the electrons, protons, neutrons, X-rays and the like just sail right through (Figure 4). It’s not like throwing pebbles at a plaster wall; it is like throwing pebbles at a chicken-wire fence (Figure 5).

The thicker you make the foil — for instance, if you stack more and more pieces of foil together — the more likely it becomes that the particles you are firing at the aluminum will hit something, lose energy, bounce back, change direction, or perhaps even stop. The same would be true if you had layer upon layer of chicken-wire fencing (Figure 6). And just as you could figure out, from how far an average pebble could make it through the layered fences, how big the gaps are in the fence, scientists can work out, from the distance traveled by electrons or atomic nuclei through matter, how empty an atom is.
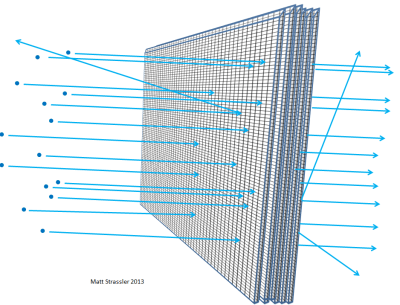
Through experiments of this type, physicists in the early 20th century figured out that nothing inside an atom — neither atomic nuclei nor electrons — can be more than a thousandth of a millionth of a millionth of a meter across, 100,000 times smaller in radius than atoms themselves. (The fact that it is the nuclei that are of this size, and that electrons are at least 1000 times smaller, is something that we learn from other experiments, such as those in which high-energy electrons scatter off each other, or off of anti-electrons [positrons].)
[To be even more precise, I should mention that some of the particles will lose a bit of energy in a process called “ionization”, in which the electric force between the incoming particle and an electron may strip the electron off its atom. This is a long-distance effect, and is not really a collision. The resulting loss of energy is an important effect for incoming electrons, but not for incoming nuclei.]
You might wonder whether the reason the particles are passing through the foil is the same reason that bullets can pass through paper, by pushing the paper out of the way. Maybe the first few particles are just pushing the atoms aside, leaving big holes for the rest of the particles to pass through? The reason we know that’s not the case is that we can do the experiment where the particles pass into and/or out of a container made of metal or glass, inside of which is a vacuum. If, as the particles passed through the container’s walls, they created holes larger than atoms, air molecules would rush in, and the vacuum would be lost. But when an experiment like this is done, the vacuum remains intact!
It’s also not too hard to tell that a nucleus is a loosely organized clump, inside of which the nucleons retain their identity. We can already guess this from the fact that the mass of a nucleus is very nearly the sum of the masses of the protons and neutrons that it contains. This fact is true of atoms and of molecules too — their masses are almost equal to the sum of the masses of their constituents, except for a small correction due to something called “binding energy” [not an essential concept in this article] — and this is reflected in the fact that it is relatively easy to break molecules into their atoms (for example, by heating them so that they bang into each other more forcefully) and to break electrons off of atoms (again by heating.) In a similar way, it is relatively easy to break nuclei into pieces, a process called “fission”, or to assemble nuclei from smaller nuclei or individual nucleons, a process called “fusion”. For example, relatively slow-moving protons or small nuclei crashing into a larger nucleus can break that nucleus apart; there’s no need for the impinging particles to be moving near the speed of light.

To understand that this isn’t inevitable, let me mention that we’ll see that these properties are not true of protons and neutrons themselves. The proton mass is not roughly equal to the sum of the masses of the objects that it contains; there is no way to break the proton into pieces; and to get the proton to do anything interesting requires energies comparable to the mass-energy of the proton itself. Molecules, atoms and nuclei are comparatively simple; the proton and the neutron are extremely complex.
Now that we know a nucleus is tiny, we have to ask an obvious question: why is it so small? [Coming soon]


35 Responses
do not want to check the correctness of the charge of the platinum core, which Chadwick had 78, and in this table is 82 …
https://fhenadzi.wordpress.com corrected table of elements.
It’s great that you are getting ideas from this paragraph as
well as from our dialogue made here.
Magistral, formato de tu blog! ¿Cuanto tiempo llevas bloggeando? haces que leer en tu blog sea entretenido. El uso total de tu web es magnífico, al igual que el material contenido!
Saludos
About the table of elements, new numbers of any elements
http://hfilipen-talentedchildren.blogspot.com
https://natureofchemicalelements.blogspot.com in Russian and in English
Wonderful goods from you, man. I’ve understand your stuff
previous to and you’re just extremely fantastic.
I actually like what you have acquired here, really like what you’re stating and the way
in which you say it. You make it entertaining and you still care
for to keep it wise. I can’t wait to read far more from you.
This is really a terrific site.
The design, supply and installation of driveway gates and garden railings & Automated Gates throughout the UK.
I guess another way to think of it is that an Electron is an indivisible unit of negatively charged Electricity. So a Photon is an indivisible unit of light. The other fundamental particles are indivisible units of “something”. At the end of the day, water is not solid so i don’t see why quanta have to be.
Also, we are so intrinsically entwined into reality with each other that we can not look at it objectively. So, whatever they “really” are is a complete mystery. One could say, we do not really know what anything is !
Particles must just be crystallised energy. That’s how I make sense of the physical side of quantum mechanics.
But what then does ‘crystallized’ mean? Particles are not still, nor solid and those with an internal structure lack the regular, unchanging and ordered internal structure of crystals.
I think it would be helpful to explain why bulk matter and visible light _can’t_ pass through a thin sheet of metal foil, and perhaps also why SEM and AFM imagery shows atoms as if they were little billiard balls. (I know the answers to these questions myself, but the reader that this seems to be pitched at won’t.)
I understand that electron orbitals are clouds. But particles are discrete. I understand that calling them “point like particles” does not mean they are tiny points. I understand that fundamental particles have no structure. But, i have a hard time not thinking of them as solid!
That’s not too much of a problem, the ‘billiard balls’ model works fine at a distance.
But I think the lack of solidity is a big problem in people’s conception of quanta. There seems to be a feeling that these phenomena are somehow ephemeral and not quite real, that they can vanish without warning or break the rules.
But quanta *are* quite solid, you can’t split them or have half of them or make them vanish all of a sudden without consequence. They have (relatively) fixed speeds and masses and move about often as if they were little balls. Most of the ‘weirdness’ is just due to the fact that they don’t occupy a fixed volume of space. Their solidity, to me, has always seemed like everything *but* a solid surface.
But possibly the professor can provide a better mental picture.
In part they seem solid because the interactions that one would think of as collisions happen as you get two particles close enough. If you think of two points with positive electric charge, they’ll push each other apart even though they don’t “touch” directly.
Also, particles are both clouds and points because the positions are probabilistic. The point can be anywhere; it’s just likely to be close to the middle of the cloud of probabilities.
Thanks for this article. I actually had an interesting discussion yesterday over a beer on how the residual of the strong force can have a limited range / become weaker than the electromagnetic force at long distances yet be strong enough to keep nuclei together at short distances. (How geeky is discussing stuff like this over beer… ;)) The gluon is massless so the force associated with it should be infinite in range. I won’t spoil the next article, but the Wikipedia page on the strong force explains it very well.
Thanks Professor, very interesting reading. Though, I still have a hard time trying to visualize what Atoms and subatomic particles are. I can still think of them as being little round billiard balls ! I know that they are not and that they are not solid. So what would be the best way to think of them as ? Would i be right in saying, we observe points in space with individual charges and other characteristics and then name them accordingly ? Cheers
It would be wrong to think of ‘points in space’ with certain properties being labelled as particles. For one thing, no particle is a point in the way we usually think of it. (Electrons are believed to be point particles, but this does not mean they occupy a tiny, point-like area of space.) I have found it useful to think of them as fuzzy clouds that look like solid balls from a distance. This is how electrons are commonly viewed for example: http://chemicalfacts4u.blogspot.co.nz/2011/06/atomic-orbital.html
A very succinct and informative article.