Neutrinos — just like the charged leptons (electron, muon, tau), the up-type quarks (up, charm, top), and the down-type quarks (down, strange, bottom) — come in three types. But there’s more than one way to divide them up. And thanks to the quantum nature of our world, you can only use one way at a time. In this article I’ll explain this remark, and how a very interesting and scientifically crucial phenomenon — neutrino oscillations — arises from this fact.
You probably think of particles as having a definite mass — all electrons have a mass-energy (E=m c2) of 0.000511 GeV — and from one point of view, the three types of neutrinos are no exception. We can classify the three neutrinos by their masses (still largely unknown, see below), and call them, from lightest to heaviest, neutrino-1, neutrino-2 and neutrino-3. We’ll call this the mass-classification, and these types of neutrinos as mass-type.

But another way to classify the neutrinos is by how they are connected with the charged leptons (the electron, the muon and the tau.) [This shows up in my article on what the known particles would look like if the Higgs field were zero.] The best way to understand this is to focus on how the neutrinos are affected by the weak nuclear force, which is reflected in their interactions with the W particle. A W particle is very heavy, and if you make one, it can sometimes decay (see Figure 1) to one of the three charged anti-leptons and one of the three neutrinos. If the W decays to an anti-tau, the neutrino produced in association with it is a tau-neutrino. Similarly, if the W decays to an anti-muon, a muon-neutrino is emitted. (As is crucial in making a neutrino beam, a pion decays through the weak interactions, and positively-charged pions make an anti-muon and a muon-neutrino.) And if the W decays to a positron, out comes an electron-neutrino. We’ll call this the weak-classification, and these neutrinos weak-type, since it is the weak nuclear force that determines their details.
What’s the big deal? We use multiple classifications of people all the time. We talk about people being young, middle-aged and old; or we talk about them being tall, average-height and short. But with people, we can always separate them further, if we choose, into nine categories: young and tall, young and average-height, middle-aged and short, old and short, etc. Yet quantum mechanics prohibits us from doing the same for these neutrino classifications. There is no such thing as a neutrino that is both a muon-neutrino and a neutrino-1; there is no such thing as a tau-neutrino-3. If I tell you a neutrino’s mass (and therefore that it is neutrino-1, -2 or -3) I simply cannot tell you if it is an electron-, muon- or tau-neutrino. In fact, a neutrino of definite mass-type is a mixture, or “superposition”, of the three weak-type neutrinos. Each mass-type neutrino — neutrino-1, neutrino-2 and neutrino-3 — is a precise but different mixture of electron-, muon- and tau-neutrino.
The reverse is also true. If I see a pion decay to an anti-muon and a neutrino, I know immediately that the neutrino emitted was a muon-neutrino — but I can’t know its mass, because it is a mixture of neutrino-1, neutrino-2 and neutrino-3. The electron-neutrino and tau-neutrino are also precise but different mixtures of the three neutrinos of definite mass.
The relation between these mass-types and weak-types is more like (but not exactly like) the relation between classifying highways as “north/south” and “east/west”, (as the US government does, assigning odd numbers to N/S highways and even to E/W roads) versus describing them as “north-east/south-west” or “south-east/north-west”. There might be good reasons to use either one: the N/S-E/W classification is good if you want to focus on latitude and longitude, while NE/SW-SE/NW might be more convenient in the vicinity of a coastline that itself runs from southwest to northeast. But either way, you cannot use both classifications at the same time. A northeastward road is both partly a north road and partly an east road; you cannot say it is one or the other. And a northward road is a mixture of a northeast road and a northwest road. So it is with neutrinos: a mass-type neutrino is a mixture of weak-type neutrinos, and a weak-type neutrino is similarly a mixture of mass-type neutrinos. (Where this breaks down as an analogy is that you could, if you wanted, use a more refined four-category N/S-NE/SW-E/W-SE/NW classification for roads; the analogous option is not available for neutrinos.)
This inability to classify a neutrino as being of definite mass-type and of definite weak-type simultaneously is an example of the “Uncertainty Principle”, similar to the weirdness that makes it impossible to know the position of a particle exactly and simultaneously know the particle’s velocity exactly. If you know one of these quantities perfectly, you have no clear knowledge of the other. Or you can learn something, but not everything, about both. Quantum mechanics tells you exactly how well you can balance your knowledge against your ignorance. By the way, these issues aren’t special to neutrinos. They occur with some other particles too. But they are especially important for the behavior of neutrinos.
A few decades ago, times were simpler. Then it was thought neutrinos might be massless, in which case the weak-type neutrino classification would suffice. And if you look at old papers or at old books for lay-people, you’ll see only the names electron-neutrino, muon-neutrino and tau-neutrino. However, after the discoveries of the 1990s, this no longer suffices.
Now here’s where it starts to get interesting. Suppose you start with a high-energy neutrino of electron-type, so that it is a particular mixture of neutrino-one, neutrino-two and neutrino-three. The neutrino propagates through space, but within it, its three different mass-types travel at very, very slightly different velocities, all of them very close to the speed of light. Why is that? Because the speed of an object depends both on its energy and on its mass, and the three mass-types have different masses. [Click here for the relevant (simple) formulas.] The velocity difference is super tiny for any neutrinos we have a hope of measuring — it’s never been observed — but it has a surprising and big effect anyway!
And here’s where it goes from just interesting to very weird.
This very tiny difference in velocities causes the precise mixture of neutrino-1, neutrino-2 and neutrino-3 that makes an electron-neutrino to change gradually as the neutrino moves through space. And that means that the electron-neutrino that we start with is, after a while, no longer an electron-neutrino, which corresponded to one very particular mixture of the neutrino-1, -2, and -3. The different masses of the three mass-type neutrinos cause the original electron-neutrino, as it travels, to become a mixture of a electron-neutrino with a muon-neutrino and a tau-neutrino. The amount of mixing depends on the differences in velocities, and hence on the energy of the original neutrino and on the difference in the masses (actually the difference between the squares of the masses) of the neutrinos.

Initially the effect increases as the neutrino travels. But curiously, as sketched in Figure 2, this effect doesn’t just grow and grow. It grows, and then it shrinks again, and then grows again, and shrinks, over and over, as the neutrino moves along. This is called neutrino oscillations. How exactly the oscillations happen depends on what the masses of the neutrinos are and how the mass-type neutrinos and the weak-type neutrinos are mixtures of one another.
The effect of the oscillation can be measured because an electron-neutrino, when it collides with a nucleus (which is how neutrinos can be detected) can turn into an electron, but not a muon or tau, while a muon-neutrino can turn into a muon but not an electron or tau. Thus if one starts with a muon-neutrino beam, and some of the neutrinos in the beam, after traveling some distance, strike a nucleus and are converted into an electron, then it means that oscillation is taking place and muon-neutrinos are turning into electron-neutrinos.
There’s one more really important effect that complicates and enriches the story. Because ordinary matter is made from electrons but not from muons and taus, electron-neutrinos have different interactions with ordinary matter than muon- and tau-neutrinos do. These interactions, which occur through the weak nuclear force, are really, really tiny. But if a neutrino passes through a great deal of matter (such as a substantial fraction of the earth or sun) these small effects can add up and have a big impact on the oscillations. Fortunately, we know enough about the weak nuclear force to predict this effect in detail, and to work backwards from what we measure in an experiment to figure out what the neutrinos’ properties must be.
All if this involves quantum mechanics. If it doesn’t seem intuitive to you, relax; it isn’t intuitive to me either. Any intuition I have I learned from the equations.
It turns out that careful measurements of neutrino oscillations are in fact the fastest way to learn about the properties of neutrinos! Nobel prizes have already been won for this work. Indeed, the whole story I’ve been telling you arose out of a classic interplay between experiment and theory that has stretched from the 1960s through to the present. Let me mention a number of important measurements that have been crucial.
For one thing, we can study electron-neutrinos produced in the center of the sun, in its well-understood nuclear furnace. These neutrinos travel outward through the sun and through empty space to earth. It has been found that by the time the neutrinos arrive at the earth, they are just about as likely to be of muon- or tau-type as of electron-type. That by itself is evidence for neutrino oscillation, and the detailed pattern gives us some precise information about the neutrinos.
We also have muon-neutrinos produced in the decay of pions that are in turn produced in cosmic rays. (High energy particles from space hit atomic nuclei high up in the atmosphere; the showers of debris include many pions, many of which decay to muon-neutrinos and anti-muons, or to muon-anti-neutrinos and muons.) Some of these neutrinos (and anti-neutrinos) are detected in our neutrino detectors, and we can see what fraction of them are electron-neutrinos (and anti-neutrinos) as a function of how much earth they traveled through to get to the detectors. Again, this gives us significant insights into how neutrinos behave.
These “solar” and “atmospheric” neutrinos have taught us much about neutrinos in the last twenty years (and the first hint of something interesting goes back nearly 50 years.) And these natural neutrino sources have been supplemented by numerous studies done with neutrino beams, such as the one used in the OPERA experiment, and with neutrinos from ordinary nuclear reactors. Each of these measurements has largely agreed with the standard interpretation of the solar and atmospheric neutrinos, and has allowed more precise measurements of the mixtures of the mass-type and weak-type neutrinos and the differences of the squares of the mass-type neutrinos’ masses.
As you would expect with any group of experiments, there are some small discrepancies from theoretical expectations, but none of them have been confirmed, and most if not all are probably just statistical accidents or experimental problems. So far there is nothing that has been confirmed by multiple experiments that contradicts this understanding of neutrinos and their behavior. But conversely, this picture is new enough and poorly-enough tested that it is possible, though perhaps unlikely, that there are completely different interpretations. Indeed some serious alternatives have been suggested. So clarifying the details of neutrino properties remains an area of active research, one in which a consensus has been emerging but in which some substantial questions remain open — including determining the neutrino masses once and for all.


87 Responses
Considering the different velocities of the component masses and the densities of neutrinos in open space would it be possible for the “mass component” of a neutrino travelling through space to exchange with the mass component of another neutrino before it separates from the original neutrino it was travelling with and what effect would this “coupling action” have on the overall picture of neutrino oscillations.
New to your site. Very interesting. Can you please date your article(s) – or did I miss it?
You could definitely see your skills in the article you write.
The arena hopes for more passionate writers such as you
who are not afraid to say how they believe.
At all times go after your heart.
Hi Matt:
I’m not sure you’re still monitoring your posts, due to your recent move. But, lately, I’ve been reading up on the LNSD and MiniBoone experiments. MiniBoone basically refuted the anomalous LSND results, implying a sterile neutrino, but came up with a small anomaly of their own. In the low energy sector MiniBoone saw some “excess events”, by which I think they meant more electron-antineutrinos than expected. I haven’t heard of any follow-up experiments to resolve this.
As you take these courses, real life scuba diving is carried
out. This training course helps yourself to operate on your diving
skill and much better them each day. They have a great tropical pool, a social clubhouse with free Wi – Fi
and the required bar for divers.
Thank you, thank you, thank you. I just finished an entire book about neutrinos, and not once does the author explain what it means for a neutrino to be associated with another particle. I cannot tell you what a relief it is to have found your article.
It’s awesome for me to have a website, which is helpful designed for my experience.
thanks admin
The Egyptian television and the Middle East News Agency
confirmed this information. I’ll tell you something about yourselves, about the REAL reason you find me “too good to be true,” at least as anything but a fool, deontologically
speaking: The real reason, from beneath all your snarlingly-hysterical cynicism against me, has rather to
do with the fact that all YOU know how to do is SUBCONSCIOUSLY PROJECT your own PETTY SELFISHNESS onto me.
The only thing any of you really care about is YOUR OWN POSITION at any cost to others, while all I have to preoccupy me is THE TRUTH; regardless of how brazenly
and cynically, sneeringly you dare to defy every Sacred Principle for which you claim to
stand, by punishing me for it just because you physically and, of course, no less “legally” can.
One question I have: is the new evidence in favor of sterile antineutrinos, or sterile neutrinos, or both? Is there mainly evidence that only antineutrinos change into sterile neutrinos before changing flavor? Or is there any evidence at all that neutrinos change into sterile neutrinos before changing? (http://www.nature.com/news/2011/110401/full/news.2011.202.html). Is this wierd violation of symmetry o.k. with most physicists?
MiniBooNE’s quest for sterile neutrinos has been a mixed bag. Back in ’07, they announced results that didn’t bode well for sterile neutrinos ( http://www.aps.org/publications/apsnews/200706/miniboone.cfm ), but this was followed in 2010 by results which kept the possibility alive ( http://www.newscientist.com/article/dn19072-sterile-neutrino-back-from-the-dead.html ). Resolving these (and other) inconsistencies is one reason that the experiment’s successor, MicroBooNE is being planned.
As for the three neutrino flavors cancelling each other out for a net “flavorlessness,” I’m a bit dubious about that. I could easily be mistaken, but it seems to me that the flavor math would need to work a bit more like the color charges of the strong interaction for that to be the case. Wrong symmetry group.
Glen, the clarity of your answers to C. E. Whitehead’s excellent questions was wonderful. I only have a general, mostly non-mathematical, knowledge of physics, and it cleared up some confusion in my mind. But, I have one additional question, besides the one below. Wasn’t the existence of sterile neutrinos conclusively disproven by the results of the Miniboone Project?
For the last several days I had been thinking about oscillating neutrinos being entangled with their interaction particles, when I clicked on this link (http://arxiv.org/abs/1006.2372), and saw that the idea had already been studied two years ago in 2010. I was thinking that the entanglement would be such that the net quantity of each neutrino flavor is exactly zero, at any given instant, throughout the Universe. Thus neutrino flavors would be conserved like many other quantities in physics; such as electric charge, which is supposed to have a net value of zero throughout the Universe. Could this be a possibility?
No, sterile neutrinos are not ruled out — experiments NEVER rule out things so definitively. They rule out certain types of sterile neutrinos with certain types of interactions. “Conclusive disproof” can be made for showing that another experiment is wrong, but for ideas, most experiments can only constrain them, not exclude them.
Neutrino flavor is known not to be conserved; that’s what neutrino oscillations are all about. You start with a bunch of electron neutrinos produced in the sun, but by the time they get to earth you have roughly equal mixtures of electron, muon and tau neutrinos.
Just realized the oscillation the author of the above article was talking about was oscillation into a hypothetical 4th type of neutrino, dubbed a sterile neutrino. So, the MinBooNE experiment basically disproved the existence of this exotic neutrino, that data in the LSND experiment seemed to suggest might exist.
According to this post on Cosmic Variance http://blogs.discovermagazine.com/cosmicvariance/2007/04/11/miniboone-neutrino-result-guest-blog-from-heather-ray/ , neutrino oscillation was not observed in the MiniBooNE experiment. To quote from the article: “The MiniBooNE neutrino data set agrees with the no neutrino oscillation hypothesis, in the range of reconstructed neutrino energy from 475 MeV to 3 GeV. ” So, could it be that neutrino oscillation doesn’t occur above a certain energy level? I know that the evidence for neutrino oscillation is on solid ground for lower energy neutrinos from the sun and other experiments that did not probe such high energies.
Matt, I’ve published my speculative theory on a personal website; http://starflight1.freeyellow.com/Multigeneration.html You mention that the electron neutrino is not the carrier of weak electric charge. There was a Scientific American article, if I remember correctly, that said it had weak charge. I’ll try to find that article. I believe that’s what made me feel justified to use the analogy with electric charge.
Intuitively, it also seemed logical to me that since the weak force only extends to about 10 to the minus 16 centimeters, that perhaps the synthesis of weak magnetic pole charges, or weak monopoles, at relatively modest energies, was much more likely than with the infinite range electromagnetic field. My thinking was that you only had to rein in, and rearrange, a dipole field from a small finite distance, rather than an infinite distance. Sort of like an exercise in Origami, or those Transformer toys that kids play with, changing them from one object to another.
I don’t have any issue with the decay of the muon, which preserves it’s ‘muonness’ by the emission of a muon neutrino (a.k.a. weak south monopole), along with an electron and electron antineutrino.
The theory is simplicity itself: The electron neutrino is assumed to carry a quantum of weak charge, which for analogy with the electromagnetic field, I call ‘weak electric charge’. Since the electron neutrino has spin, I assume there is a corresponding ‘weak magnetic dipole field’ enveloping it, and extending to 10 to the minus 16 cm. At sufficient energy it’s assumed that the weak magnetic dipole field can be split into an isolated pair consisting of a weak north and a weak south monopoles. Or, alternatively, pairs of weak north-antinorth, or weak south-antisouth monopoles could be created. The key point here is that in this pair creation there is no net weak magnetic charge, it always adds up to zero. Thus it constitutes a conservation law, just like so many others in physics – energy, momentum, spin, charge, etc.
Neutrino oscillation also does not conflict with this theory, provided that at any given instant the number of muon neutrinos (a.k.a. weak south monopoles), from a given source – sun, star, reactor, is exactly equal to the number of tau neutrinos (a.k.a. weak north monopoles). Such correlation would be entirely possible with Quantum Mechanics. For example it’s known that in lab experiments where the spin of two photons are correlated, that no matter how far apart they are, when one is measured, the other will instantly have the correct correlated spin, even if they are on opposite sides of the Universe.
Science doesn’t work by somebody saying: “Look, here I have this cool idea!” Rather, a scientific theory should make verifiable predictions.
In fact, you have made a verifiable prediction above: you predict that any given reaction will produce the same number of muon and tauon neutrinos. I say that this prediction is blatantly false. For example, a muon decays into an electron; as a side effect, it also produces a muon neutrino, an electron antineutrino, and no tauon neutrinos. Likewise, a tauon may decay into an electron or a muon (producing an appropriate neutrino-antineutrino pair). It can also decay into a negatively charged pion (with or without more neutral pions and/or pairs of negative and positive pions), plus a tauon neutrino – with no electron or muon neutrinos. No muon/tauon symmetry here.
For people interested in neutrino oscillation, as I am, there’s a really good site that serves as a kind of clearing house for this remarkable phenomena: http://www.hep.anl.gov/ndk/hypertext/ It seems to cover most of the experiments ever done to detect neutrino oscillation, or planned for the future.
Matt, thanks for the explanation on neutrino masses and providing the link to the Particle Data Book. For what it’s worth, here is the link to my short, speculative paper on the ‘weak’ magnetic monopole idea, not to be confused with the neutrino’s magnetic moment, which is entirely different. http://starflight1.freeyellow.com/Multigeneration.html The particle interaction referred to in the paper is on page 115 of “Introduction to High Energy Physics” by Donald Perkins.
I noticed that you mentioned String Theory among the 75 papers you have authored. I was extremely excited when I first read about the extra dimension spin-off of String Theory, by Arkani-Hamed, Divali, and Dimopoulos in 1998. Since then, the idea has evolved greatly with hundreds of papers. I especially was interested in the Randall-Sundrum variants. Have you done any papers on the extra dimension(s) ideas?
No coatnmilps on this end, simply a good piece.
Shoudn’t it be possible to work backwards from the measured amount of oscillation of solar and reactor neutrinos to estimate the masses of the electron, muon, and tau neutrinos? And have such estimates been published anywhere?
It turns out the neutrino oscillations only tell us the differences of the squares of the neutrino masses — which isn’t quite enough information. We need a different type of measurement to actually get the mass of one of the neutrinos, which then (knowing the differences from oscillations) will tell us the other two.
This information lies at the core of all the measurements and is widely published. A review of the subject (very extensive) is found in the Particle Data Book 13th chapter: http://pdg.lbl.gov/2012/reviews/rpp2012-rev-neutrino-mixing.pdf . See figure 13.6 (difference of mass squared of tau- and muon- neutrinos), Table 13.7, and discussion following equation 13.81. You can also look at the references they cite. You’ll see that much is known, much remains to be known, and very active efforts are continuing to close the gaps in our knowledge.
I thought of a simple idea to explain the origin of the two higher generation neutrinos. If one thinks of the electron neutrino as the carrier of ‘weak’ electric charge, then there may also exist ‘weak’ magnetic charge. Assuming this ‘weak’ magnetic field had two poles ‘weak’ north and ‘weak’ south – one would correspond to the muon neutrino, the other to the tau neutrino. This assumes that such pole charges can exist in isolation like the hypothetical Dirac monopole. Thus the limit of two, and only two, extra neutrino flavors, barring the existence of the sterile neutrino.
One fallout of this idea, (assuming ‘weak’ magnetic charge is conserved), is that the decay of particles carrying the higher generation flavors (strangeness, charm, topness, beauty), would conserve those flavors via a muon or tau neutrino (or their antiparticle) among the decay products, rather than those flavors simply disappearing. More recently, this made me wonder if a process like this could be masquerading as neutrino oscillation or disappearance. I also took into account spin conservation.
I submitted a paper, discussing the original ‘weak’ magnetic pole idea, but not including the oscillation/disappearance idea, to two separate journals in 1994, but neither published it. I studied a total of 10, flavor changing decay, bubble chamber photographs, from Brookhaven in which one unit of strangeness was dissapated. Six on initial inspection appeared to have some momentum disparity. On one of these, a Lambda decay, I carefully measured the initial particle track angles and worked up the numbers. The visible decay products showed a momentum discrepancy based on the method of analysis used.
I’m planning to publish the paper shortly on my own website: http://starflight1.freeyellow.com This will include all diagrams and the way the measurement of momentum was carried out.
Good luck. You’re going to need it, since nature isn’t possibly going to agree with these ideas. You would do better to study the Standard Model and the particle data book at lot more carefully before launching your website, but I doubt you will pay attention to reason.
The reason your idea fails on line one is that the electron neutrino is NOT the carrier of weak electric charge, first of all; and second, if the muon neutrino were to weak magnetic charge (which is well understood) as the electron neutrino is to weak electric charge, then the decays of muons (which are extremely well understood) would be completely different from what they are measured to be. Electrons and muons differ only in their mass; similarly for their neutrinos, which is why neutrino oscillations are possible.
One other note: my problem with neutrinos for “dark matter” is they are too fast maybe for some instances; however they are a possible candidate’; perhaps there is more than neutrinos though.
That is the biggest objection, and is completely valid for accounting for galactic DM halos or the structure of clusters. Most neutrinos would be far too energetic to remain gravitationally bound to such a localized region. However, a small portion of neutrinos would be “cold neutrinos” (neutrinos associated with the tail-end of the beta decay energy spectrum, near the predicted value for beta particle energies without neutrinos carrying away energy) which would not have this problem (and which would be even more difficult to detect than “hot” neutrinos since they really aren’t energetic enough to participate in subsequent weak interactions). The big question is whether there would be enough of them to make a significant contribution, and, if so, how much.
So you are saying that neutrinos are pretty unique! However, I do note that someone has supposedly created “majroana particles” — which according to the information here are “quasi particles” like the “holes” in matter created by the flow of electrons (the holes IMO get a net positive charge and act thus as postively-chared particles): http://news.yahoo.com/mysterious-particle-found-decades-searching-130005728.html Back to the role of neutrinos (if there is one) in “dark energy;” there do in fact seem to be other explanations for things like the “velocity anomaly” in the local galaxies; see: http://arxiv.org/abs/0708.2449 — but it’s stuff like this that makes the idea of “repulsive gravity” attractive and I still wonder if having opposite-directioned spins and being otherwise identicle is important)
Don’t get too excited about creating Majorana quasi-particles in the lab; aside from the fact that this doesn’t actually tell us anything about neutrinos (solid-state physicists make all sorts of quasi-particles in the lab all the time, with no implications for particle physics), the Majorana quasi-particles they made this time don’t even move.
(That last sentence should end, “as I understand things.” Sorry.)
Hmm, I thought that neutrinos’ and antineutrinos’ spins/chiralties had already been measured some way (see http://www.lbl.gov/Publications/YOS/Mar/neutrinos-2.html : “neutrinos always spin left and antineutrinos always spin right. “Spin” isn’t Newtonian rotation, however, it’s a quantum number”), but apparently the measurements depend on whether or not the sterile neutrino exists. This I do not know.
Next and final question is: do other particles are their own antiparticle and that hence apparently get a Majorana mass (as neutrinos and antineutrinos may get) have chiralties that are opposite (for the particle and its antiparticle)?
Incidentally, regarding Villata’s repulsive energy, I do wonder about the neutrinos as a candidate for this, simply because neutrinos’ density/mass/number is consistent with what is currently expected for dark energy, as I understand thins.
Neutrino chirality has indeed been measured, and neutrinos are always left-handed, and anti-neutrinos are always right-handed. In general, the Standard Model describes most particles as being a superposition of chiralities, but that does not seem to apply to neutrinos (unless sterile neutrinos exist, but these are currently considered hypothetical in the absence of firm experimental evidence) since the weak force won’t interact with right-handed neutrinos or left-handed anti-neutrinos. This is a pretty complicated topic, and it is rather easy to get pretty deep into the weeds. The relationship between chirality and particles and anti-particles quickly gets caught up in discrete symmetries (charge conjugation C and parity P operators, which a change in chirality corresponding to a parity operation, but the relation between matter and anti-matter requiring both C and P).
The only other non-composite particles that I can think of off the top of my head that are considered their own anti-particles (and I could easily be forgetting something) are the photon, but, being massless, it is a rather special case, and the Z boson, which, since it couples to the Higgs field, would be a mix of LH and RH chirality.
Regarding Villata’s ideas, I don’t really see a mechanism for neutrinos to provide cosmological expansion pressure. Vacuum energy (which we know to exist) seems a much better candidate for explaining dark energy. On the other hand, neutrinos have long been a popular candidate for making up at least some small portion of dark matter.
A couple of corrections: your statement about the Z isn’t right, because massive spin-one particles have three spin-states, not two, and those are helicity states, not chirality states. Chirality is a property of fermions; helicity applies to every particle with non-zero spin. (I really try to avoid this level of technical detail here; please consider moving discussions of this type to the Technical Zone part of the website, as this scares off non-experts.)
Thanks for the correction, Prof. Strassler. I had a sneaking feeling I was overlooking something when I brought up the Z.
I hadn’t really paid attention to the Technical Zone. I’ll definitely have to check it out.
That’s really my fault; I haven’t developed it properly.
That’s not a problem. I know your day job keeps you pretty busy.
Thanks. So matter and antimatter necessarily are opposed in terms of chirality? (That’s my understanding; no need to reply unless it’s wrong.)
In general, no, although that happens to be the case with neutrinos (assuming that sterile neutrinos don’t exist). For a little more insight, take a look at the URL I referenced earlier and note the role that chirality plays in the Higgs interaction.
Thanks once more; I met “dark energy,” you are correct. (I am very bad with terminology, very bad.) I do have a question, neutrinos and antineutrinos, the type we are talking about have different chiralities. Do they also have different helicities (these are, IMO, slightly different things, though both refer to spins)? No hurry to answer. Thanks.
That is a wonderful question. For massless particles, helicity and chirality are the same. For particles with mass (which seems to be the case with neutrinos), it is always theoretically possible to “boost” into a reference frame where the particle’s helicity reverses, but chirality remains invariant regardless of reference frame. So, for particles with mass, helicity depends upon reference frame.
Flip Tanedo (a grad student at Cornell) has a wonderful blog post discussing the differences and similarities of helicity and chirality. I highly recommend it, along with all of his articles. They provide a lovely crash-course on the Standard Model in very accessible terms.
The link you provided explained the Higgs far better than any post on this site I have encountered. Many thanks, I think I now have some solid grasp on how the many massless fundamental particles became the fewer massive ones.
One more question: are antineutrinos very abundant? I assume that, unlike other antimatter, they are. If so, what does anyone think of the theory that antimatter such as antineutrinos is repelling other matter, and that this, instead of so-called “dark matter” is what causes the universe’s accelerated expansion? (see phys.org/news/2012-01-repulsive-gravity-alternative-dark-energy.html). Personally I find this an attractive theory.
Anti-neutrinos are fairly abundant, and are produced in some of the more common types of beta decay reactions.
Be careful not to conflate “dark matter” and “dark energy.” They are two very different concepts.
Experimentally, there is currently no evidence that gravitational interaction with anti-matter is any different than with normal matter. It is always attractive. (Work is currently underway at CERN to verify this by performing experiments with anti-hydrogen.) Nor would we expect otherwise from a theoretical basis in terms of how anti-matter pops out of the Dirac equation. Villata is incorrect (or at the very least well outside of the mainstream in his interpretation of general relativity) in stating that general relativity predicts that matter and anti-matter would repulse one another.
O.k. thanks; the explanation that the neutrinos oscillated, not decayed, makes sense of course (“decay” is the of wording in some online articles; that’s how I got confused here). The math looks interesting; I suppose that V approaches C but is never C unless the mass is 0,so it is approaching C as the mass approaches 0. The rest of the math looks interesting, but Calculus is still not easy for me, so I’ll need time to go through it (I can make sense of the basic equations for waves but I am sure I can slowly work through this). One more question for you: the neutrino flavors have different chiralities, no, there are only two allowed, one for the neutrino, one for the antineutrino, and any others would not interact via the weak force? But they all have different weak force interactions, different wavelengths associated with them when they are involved in a reaction? Is this it? Thanks much to you for your quick reply?
Only left-handed neutrinos and right-handed anti-neutrinos couple to the weak force. Right-handed neutrinos or left-handed anti-neutrinos (if they exist) do not, and would be what are referred to as sterile neutrinos and would be non-interacting (except through gravity).
Hi, I am not a physicist nor even a physics student, but I am working on an online article that deals with neutrino mixing and mass and am trying to get this right:
1). Are you saying that the composite or superposition is not like the directions North and East being related to North Northeast and East Northeast, because while you have the components of all three distinct particles they do not mix but change flavor; thus there are only three discrete possibilities?.
2). I am assuming then that something somehow determines what “flavor” of interaction the composite or superposition of three neutrino weak interaction flavors has at any given time.What force/particle determines the flavor, according to current theory? Or is this still an unknown?
3), Apparently it seems here for there to be three mass types, there must also be three weak-interaction flavors, a kind of symmetry? Is this a correct assumption here?
4). Are each of the weak-interaction flavors associated with particular mass types. so when you say that the neutrino we “observe” changes flavors, what you mean is that it changes weak type interaction but in doing so can signal a change in mass, even though we cannot measure the mass at that point?
5). This discussion apparently does not take into account the proposed sterile neutrinos, which do not interact via the weak force? Yet apparently neutrinos can also change into sterile neutrinos and/or vice versa? So are there really at least four component neutrinos here, with the sterile neutrino having no weak interaction but still being a component, or should the sterile neutrino, if it exists, be discounted here, since it does not interact via the weak force?
5). If sterile neutrinos don’t interact via the weak force, but only via gravity, how dophysicists propose that they change into other flavors of neutrinos?
6), I do note that matter with mass can speed up and slow down, that is change speed, that is any particle with mass does not have only one particular speed that it can travel at; but you’re saying that it nevertheless, depending on its mass, slows down at different rates and so forth? This makes sense, but I just want to verify this.
7). These neutrinos that interact differently via the weak force get a Dirac mass right? Now suppose that neutrinos get decay into antineutrinos or vice versa, whichever way (and get a Majorana mass thus). Do the neutrino and antineutrino in this case differ only in their helicities, but not in terms of their interaction with the weak force?
(Thanks, and sorry to ask so many questions at once! Let me know if you want me to redo these and ask these questions separately.)
I can take a stab at these. Hopefully, Prof. Strassler will catch any areas where I go astray.
What Prof. Strassler was attempting to express with the road direction analogy is that the difference between neutrino flavors and masses has to do with coordinate systems. (Here, “coordinate system” means something a bit more abstract than conventional spatial coordinates, but rather “directions” in an abstract vector space of states.) Neutrinos can only be created or detected in the coordinate system corresponding to flavor, with each flavor being a mixture of mass coordinates (just as a northeasterly road can be described as a mix of north and east). But the mathematical description of neutrinos travelling through free space has to be done in terms of the mass coordinate system. Just as the flavor states can be expressed as a combination of mass states, the mass states can be expressed as a combination of flavor states. Once the neutrino is detected, we are forced to snap back to the flavor coordinates, pinning the particle to be a specific flavor, which might not be the same flavor that it was when it was produced, depending upon how far it traveled as a free particle.
As the neutrino travels, it is a mixture of all flavors, with the probability of detecting it in any one flavor varying sinusoidally, with the rate of variation being different for each flavor type. There isn’t really a force involved in picking a particle flavor. It is just the statistical probabilities inherent in quantum mechanics. The only place where a force comes into play is during the creation or absorption of the neutrino, which is through the weak nuclear force mediated by a W or Z boson. During that interaction, one flavor type is “picked” based upon the quantum probabilities.
That is correct. When the idea of neutrino oscillation was first conceived, only two neutrino types were known, the electron and muon neutrinos, so it was assumed that there would be two corresponding mass types. When the tau lepton and its corresponding neutrino were discovered, the idea was extended to encompass three mass types. The math and experiment both seem to bear out this symmetry.
Each flavor type is a mixture of all three mass types. Keep in mind that I’m talking about combinations of quantum probability amplitudes. I’m not saying that “an electron neutrino is x% mass 1, y% mass 2, and z% mass 3.” Instead, this is to say that “an electron neutrino wavefunction is x% mass 1, y% mass 2, and z% mass 3, so the probability of it being mass 1 is |x|^2, etc.”
If sterile neutrinos exist (and that is a big if), it will be found by an experimental determination that there is still a deficit in accounting for neutrinos, even taking into account oscillation. (For the technically inclined, that would mean that the PMNS matrix would be found to not be unitary.) That would mean that the mathematics for describing neutrino oscillation would have to be modified to take into account the probability of a neutrino oscillating into an undetectable sterile state.
For the uninitiated, the weak nuclear force only interacts with left-handed neutrinos or right-handed anti-neutrinos. If neutrinos with the opposite chirality exist, they would not interact with anything at all except via gravity. Since they don’t interact with the weak force, they only way that they could come into existence would be via oscillation. There is some experimental evidence for a deficit in detected neutrinos which could be explainable via sterile neutrinos, but the evidence really isn’t conclusive. This is one of the things that the Nucifer experiment will be looking into.
Remember that flavor oscillation isn’t via the weak force. Neutrino creation and detection is via the weak force, but not oscillation. If sterile neutrinos exist, the PMNS mixing matrix can be modified to account for oscillation into and out of those states.
Massive particles can certainly change speed. Remember that the speed of a massive particle depends upon its kinetic energy. Neutrino mass is so small that it doesn’t take much kinetic energy for it to move very near the speed of light, and such high speeds are the typical assumption for neutrino calculations. That said, it is certainly possible to conceive of “boosting” into a reference frame where a neutrino is moving slowly or even at rest, but, by and large, such reference frames would be moving pretty fast relative to just about everything else in the universe.
There is likely some population of “cold” neutrinos out there with such low kinetic energy that they move rather slowly, and these are considered as candidates for at least some portion of dark matter. Unfortunately, we don’t have a way of detecting them, since there is a minimum energy threshold needed for neutrino detection. It isn’t very viable to create a detector on the scale of Super Kamiokande out in space and accelerate it to relativistic velocities in the hope that it will collide with cold neutrinos.
And if you want a taste of the math, here are how the calculation are done for the case of two flavors (as was done before the discovery of the tau neutrino. The three flavor case is similar, but involves a 3×3 matrix. This is excerpted from a rather lengthy blog post that I’m working up on the topic.
Neutrino Oscillation: Two Flavors
The neutrino flavors that we know from weak interactions (the weak eigenstates) are linear combinations of underlying mass eigenstates, where the mass eigenstates (denoted as ν1 and ν2) are the free particle solutions to the wave equation. We cannot assume a priori that the mass eigenstates and flavor eigenstates are equivalent. If they are, as we shall see momentarily, oscillation cannot take place. If they are not, then these mass eigenstates cannot be directly observed in their pure form, only weak eigenstates (via the weak interaction). The weak eigenstates are related to the mass eigenstates by a simple unitary (length preserving) matrix:
This matrix relationship is simply a more compact representation of the following two equations:
In other words, the weak eigenstates are coherent linear superpositions of the mass eigenstates. Here,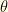 is referred to as the “mixing angle.” Note that this is simply a change in basis, completely analogous to rotating a coordinate system in an ordinary 2-D Cartesian coordinate system.
is referred to as the “mixing angle.” Note that this is simply a change in basis, completely analogous to rotating a coordinate system in an ordinary 2-D Cartesian coordinate system.
This relationship can also be inverted to give the mass eigenstates as superpositions of the flavor eigenstates:
We assume that the mass eigenstates for the free neutrino as a function of time are simply plane waves:
Suppose we have a weak decay producing an electron neutrino at time t=0. That neutrino expressed in terms of the mass eigenstates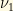 and
and  would be:
would be:
Combining this with the time-dependent representations of the mass eigenstates, and taking the direction of the neutrino’s motion to be along the z-axis, we see that the time evolution of the neutrino wavefunction is given by:
Now, looking at the beta particle energy distribution which prompted this whole neutrino business, we see that the peak is far from the cutoff (where the neutrino energy is zero), so, by and large, neutrinos are not “cold.” With their infinitesimally small mass, the bulk of the energy involved in neutrino production goes into their kinetic energy rather than rest mass. As a consequence, neutrinos can be expected to have velocities approaching (but not quite reaching) the speed of light in both the laboratory and center-of-mass reference frames. (Consideration of “cold” low-velocity neutrinos is important in the context of discussions of neutrinos as a dark matter candidate, but we will touch more upon this later.) This assumption is born out by measurements of neutrino velocities performed in the wake of the OPERA “superluminal” neutrino fiasco, including those performed by the OPERA team once they found and corrected their hardware problem. So, for mathematical simplicity, we can make the very good assumption that . This allows us to change our equation from being in terms of time into one in terms of distance by noting that
. This allows us to change our equation from being in terms of time into one in terms of distance by noting that 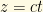 , so
, so 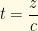 .
.
Furthermore, we know from the energy-momentum relation from special relativity the following:
For the reasons discussed above, we may assume that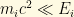 , so we can approximate the radical by taking the first two terms of its Taylor series expansion:
, so we can approximate the radical by taking the first two terms of its Taylor series expansion:
Therefore:
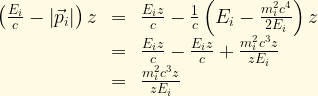
So, our expression for the wave function as a function of distance now becomes:
where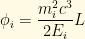 , which is simply the phase of mass eigenstate i at a distance L.
, which is simply the phase of mass eigenstate i at a distance L.
Now, expressing the mass eigenstates in terms of the weak eigenstates:
Remember that I mentioned earlier that oscillation would not occur if the flavor eigenstates and mass eigenstates were identical. That becomes very clear in this expression. That equivalence would mean that , which would result in the term for the muon neutrino going to zero.
, which would result in the term for the muon neutrino going to zero.
Likewise, it is evident at this point if all of the neutrino eigenstates have identical masses, that would mean that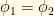 , meaning that the mass eigenstates would retain their relative phases. Again, the muon neutrino term would vanish.
, meaning that the mass eigenstates would retain their relative phases. Again, the muon neutrino term would vanish.
If the masses are different, the wave function no longer remains purely an electron neutrino. We can calculate the probability of a flavor change by taking the projection of our wave function against the muon neutrino basis component and taking the absolute square:
Where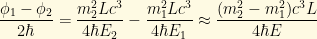
(Yeah, I had to dredge up quite a few trig identities that I’ve not used in decades. Thank goodness for Wolfram Alpha.)
Thus we find that the two-flavor oscillation probability as a function of distance L is:
where
The two-flavor survival probability is then:
The wavelength for flavor oscillation is then given by:
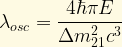
(A quick double-check of this result via dimensional analysis shows that this reduces to units of length. Wee!)
As many have said here before, forgive my ignorance, but how would you go about passing the weak-vs-mass type incongruities to the leptons? They’re particles with well defined masses and no mixing I’m told, but is this just an artifact of the way we arbitrarily give the incongruities to the neutrinos?
This is indeed an artifact. For example, in the case of the quarks, we tend (by convention) to put the incongruities in the down-type quarks and not the up-type quarks, but we could do it the other way and it wouldn’t matter. In the case of the charged leptons and neutrinos, we could do it the other way too. But it would turn out to be inconvenient in the case of doing calculations of neutrino physics… mainly because the neutrino masses are so small compared to accessible energies that their oscillation phenomena are dramatic, while effects in the charged leptons at current energies would be very minimal. So it is just convention to put the incongruities in one place rather than the other, but the practical justification for this choice is very clear.
On the question of the separation of the neutrino components due to varying velocities — you mention that with current experiments the separation isn’t big enough to measure. But I imagine for astronomically-generated neutrinos it’d be a different story. Are the neutrino masses known well enough to estimate how much (say) the Supernova 1987A neutrino components should have been separated when they arrived at Earth?
Mike Richmond has a good pedagogical presentation on the limits http://spiff.rit.edu/classes/phys200/lectures/sn1987a_2/sn1987a_2.html
If you jump to near the end you’ll see an actual paper on the subject. Limits on the electron neutrino mass from the duration of the neutrino burst are about 26 eV.
So we probably know (today) that neutrino masses are so small (probably all less than 1 eV) that there would be no measurable separation.
Insignificant nit-pick: In the US, North-South highways are given odd numbers, and East-West highways are given even numbers, at least for Interstate and US highways. You have it backwards in the analogy given in the article. Other than that, though, great analogy.
thanks for catching that!
Matt thank you for taking the time to answer our questions. We must seem like ignorant undergraduate students. I’m sure you are very busy since the holidays are over, but it’s very cool what you are doing! I’m sorry if I’m just restating when you are writing. Putting things in my own words is one way I learn.
I started reading about mixed states. In the definition of a mixed state, we don’t know which state the particle is in. It’s not even a super-position of states, because even that’s a definite state. (Is this correct? I’m not sure.) We can calculate the probability it’s in each state, but not know for certain. So for an electron neutrino, we wouldn’t know which mass it had BECAUSE it’s a mixture of those states. Likewise if we determined its mass, we wouldn’t know which type of neutrino it was: electron-type, muon-type, or tau-type. Like you said in the article, it’s like the uncertainty principle but for mass/flavor instead of momentum/position.
I’ve confused you, with wording: a “mixed state” is not what’s involved here, just a “super-position”.
Technical jargon: An electron-neutrino is a superposition of the three mass-type neutrinos; similarly, any mass-type neutrino is a superposition of the three weak-type neutrinos. The mass of the electron-neutrino is not well-defined, not because it is in a mixed state, but because it is a superposition of states that have well-defined but distinct masses.
Now, why did this confusion arise?
Part of my technical problem in running this website is that I have different audiences with different levels of experience and expectations. The term “super-position” doesn’t mean anything to a non-expert, but “mixture” does, as a word in English. So I chose (with some trepidation) to use the word “mixture” to replace the technical term “super-position”, to convey the intuitive idea of a blending together of two or more states. Of course the only way to fully understand what I mean by this is to learn the math, but still, the term at least conveys a certain idea.
However, in the term “mixed state” — which most non-experts never come across — the word “mixed” is used in its Physics-ese meaning. Much more technical and precise, and different, as you say, from superposition.
I apologize that this choice of mine causes some confusion here, but I still don’t see a good alternative for my pedagogical choice at the moment.
A superposition of states is still an ordinary quantum state, where the state is as precisely specified as is possible in quantum mechanics. A system is in a mixed state if quantum information is missing.
Thanks for clearing that up!
“The reverse is also true. If I see a pion decay to an anti-muon and a neutrino, I know immediately that the neutrino emitted was a muon-neutrino — but I can’t know its mass, because it is a mixture of neutrino-1, neutrino-2 and neutrino-3. The electron-neutrino and tau-neutrino are also precise but different mixtures of the three neutrinos of definite mass.”
If each of the weak-type neutrinos is a precise mixture of the three mass-type neutrinos, and the mass-type neutrinos each has a definite mass, doesn’t that mean that each weak-type neutrino has a definite mass? So, if we knew precisely the masses of each of the mass-type neutrinos we’d know the masses of the weak-type neutrinos?
No. This is quantum mechanics. The electron neutrino is a mixture of the three masstype states, which means it has all three masses with different probabilities. (Even that statement is not quite correct.) It does not have a definite mass: it doesn’t get an average of the three masses . If it did, there would be no oscillations.
Right, like the famed cat – each weak-type neutrino has a wave function that describes its mass. Is that correct?
This goes back to that Mass and Energy article. The three neutrinos 123 have the same energy, but different masses. So they have different momentums. Particles are also waves, so they have different wavelengths (which is related to their momentums). Their crests would thus not coincide. Since the amplitude of the wave is the probabiltiy you find it, the probability of getting any one combonation of neutrinos 123 would change the further you move from the source, and its type would change. Is this correct?
Essentially, yes.
A question regarding neutrino oscillations: Do the oscillations occur such that the heavier neutrino component becomes lighter and the lighter component becomes heavier so as to keep the neutrino from “separating” or “falling apart”, if you will allow me to use that phraseology? And if a beam of one type of neutrino were traveling unimpeded through space, do the oscillations occur in a coherent or in-phase manner, or is it rather random?
Neutrino oscillations are a coherent phenomenon. And if the distance traveled is long enough, the different components of the neutrino will separate in space because the heavier and lighter neutrinos have slightly different velocities. But this is actually quite a subtle point, still being argued in the literature, which doesn’t arise in real experiments due to the small neutrino masses. See for example http://arxiv.org/abs/arXiv:1006.2372
As always, you are truly a good teacher. You made such a complicate issue an easy read. At least, it becomes easier for me to realize some questions which might never come to my mind before. Again, the issue is the nitty-gritty of semantic meanings of some terms used in physics, such as, oscillation, entity, classification, etc.. Let me use an analogy to ask my questions.
Case 1 — Mr. A (one person) has multiple personalities.
A1 — a nice guy.
A2 — a murder.
A3 — a cry baby.
Case 2 — there are “three” gentlemen.
Mr. B — a nice guy.
Mr. C — a murder.
Mr. D — a cry baby.
In case 1, Mr. A can oscillate among A1, A2 and A3. We can call this oscillation type I or OC (I).
In case 2, there is also an oscillation mechanism among Mr. B, Mr. C and Mr. D. We can call this oscillation type II or OC (II).
Question 1 — Is there any foundational difference between the case 1 and the case 2, if those gentlemen are neutrinos? If the answer of this question is a “definitely No”, then, no further question is needed. Is this what you mean “the conflict classification”? Note: my personal opinion, the conflict classification as you described will not make case 1 and case 2 becoming indistinguishable.
Question 2 — Can OC (I) be identical to OC (II), (in their internal mechanism)?
Case 3 — there exist one “uncertainty principle” which makes the OC (I) and OC (II) indistinguishable although the case 1 and the case 2 are different in essence. We can call this type oscillation the type III or OC (III).
Case 4 — the oscillation was observed as book-keeping data, without concerning its internal mechanism. We can call this type of oscillation the type (book-keeping) or OC (bk).
Question 3 — can the term “oscillation” be used for all these four types of oscillation without any confusion?
Hi, very nice article. There is one point that I don’t understand. I thought that in relativity the mass squared commute with the hamiltonian. How come that it does not commute with the interaction terms giving all these weird oscillations?
thank you
Technical answer: Often one can write the Hamiltonian as a free part H0 and an interacting part H’. [This is not always true, but if there are nice particle states this is almost always the case.] Then H0 commutes with the masses (which means that particles that are not interacting with other particles will propagate with a definite mass) but H’ and H0 do not in general commute. So I think you were thinking of the free Hamiltonian. (Particle states are NOT exact eigenstates of the full Hamiltonian, a fact which has all sorts of important implications in quantum field theory. In fact, if they were eigenstates, then how could they ever decay?!)
“these issues aren’t special to neutrinos. They occur with some other particles too. But they are especially important for the behavior of neutrinos.”
By “these issues”, do you just mean that the Uncertainty Principle (discussed in the preceding paragraph) applies to other particles too, or are you saying that other types of particles can also (in principle) oscillate between types in this way (for example, that electrons could oscillate into muons or taus)?
If it’s only neutrinos that have these two conflicting classifications (mass vs. weak) and the resulting oscillation between types, is anything known/speculated about why they’re unique in this way?
Other types of particles do oscillate in this way, yes. In fact it is very common among composite particles made from quarks and anti-quarks. But this is a long story.
Similarly, conflicting classifications are very common too (but it’s a bit complicated.) For example, there is one conflict among the quarks. If we assert that we don’t want to have these conflicting classifications for the up-type quarks, then the down-type quarks have them; if we try to remove the conflict for the down-type quarks, then the up-type quarks have them. [In fact, we could remove the conflict from the neutrinos and give it to the charged leptons, if we wanted.] And EVERYTHING is known about why this happens; it’s a simple argument using linear algebra and counting. The effect is strange, but completely understood.
Conventionally, the conflict of mass-type versus weak-type is assigned to the neutrinos and the down-type quarks — but that’s an arbitrary choice.
The conflict of mass-type and weak-type in the quarks is essential in nature. This is why for instance, top quarks can decay to strange quarks by emitting a W particle even though at first glance you might think a W particle would only interact with a top quark and a bottom quark. The subtlety is that the top quark emits a W particle to become a weak-type bottom quark, but a weak-type bottom quark is a mixture of a mass-type bottom quark, a mass-type strange quark and a mass-type down quark. And so a mass-type top quark = weak-type top quark (remember we removed the conflict for the up, charm and top quarks) can decay to a mass-type strange quark. Similarly bottom quarks can decay to charm quarks, which would be impossible if all weak-type quarks and mass-type quarks were the same — so without this conflict there would be more stable particles than we observe.
Question: Is there any better language for describing this? With neutrinos, as you describe, you can say “electron neutrino” (i.e., weak-type) or “neutrino-1” (i.e., mass type), which makes it obvious which you’re talking about, and highlights the fact that the two are not the same; for quarks has any language developed that does the same?
There really isn’t another language, and the reason is partly accidental. It turns out that the mass-type quarks and weak-type quarks (the scientific lingo is “mass eigenstates” and “weak eigenstates”) are very similar — to within 20% — and so the names can be retained without being confused. More precisely, if we define the up, charm and top quark mass eigenstates (ordered from smallest to largest mass) to be exactly the same as the up, charm and top quark weak eigenstates (which is the usual convention, though not required), then the down, strange and bottom quark mass eigenstates, defined as objects with definite mass from smallest to largest, differ only slightly from the down, strange and bottom quark weak eigenstates, defined as those objects that a W boson will create when interacting with an up, charm or top quark.
The neutrino eigenstates, by contrast, are much more scrambled. Again, we choose (by convention) the electron, muon and tau (organized from smallest to largest mass) to have the same mass and weak eigenstates. Then the neutrino weak eigenstates (electron-neutrino, muon-neutrino, tau-neutrino) that you get when a W boson interacts with an electron, a muon or a tau are not anything close to the three neutrino mass eigenstates organized from smallest to largest mass… and so there is therefore no motivation to call the lightest neutrino the electron-neutrino mass eigenstate, in contrast to the down quark mass eigenstate which differs from the down quark weak eigenstate by only 20%.
Why the mass and weak eigenstates of quarks are so similar, while those of neutrinos are so different, isn’t known. Many theorists (including me) have speculated about it, but there’s no experimental evidence one way or another.
Hi, great article. One thing I didn’t understand: the three mass components of an electron-neutrino travel at slightly different speeds, and you say this causes the electron neutrino to oscillate into a mixture of all three weak types. But over time, would not the three components separate out in space(due to their different speeds), so that after travelling a large enough distance, one would find three mass-neutrinos at different points in space?
A final question, is would an initial mass-type neutrino oscillate into a superposition of other stuff?
Eventually, yes, they would separate… but this is a subtle subject involving the notion of quantum decoherence.. I’d have to review some fairly detailed literature to make sure I made correct statements about this. For all current experiments this doesn’t play a role, but certainly my presentation relies on some approximations whose validity at some point will break down.
An initial mass-type neutrino would not oscillate in empty space, but could still oscillate in matter, since its electron-type part would behave differently in matter than its muon- and tau-type parts, meaning that it would become a mixture of different mass-types. But this doesn’t ever arise, because the only way to make neutrinos in practice is through the weak interactions, so we always end up starting with a weak-type neutrino.