In my role as a teacher and explainer of physics, I have found that the ambiguities and subtleties of language can easily create confusion. This is especially true when well-known English words are reused in scientific contexts, where they may or may not be quite appropriate.
The word “particle”, as used to describe “elementary particles” such as electrons and quarks and photons, is arguably one such word. It risks giving the wrong impression as to what electrons etc. are really like. For this reason, I sometimes replace “particle” with the word “wavicle”, a word from the 1920s that has been getting some traction again in recent years. [I used it in my recent book, where I also emphasized the problems of language in communicating science.]
In today’s post I want to contrast the concepts of particle, wave and wavicle. What characterizes each of these notions? Understanding the answer is crucial for anyone who wants to grasp the workings of our universe.
Why “Wavicle”?
What I like about the word “wavicle” is this.
- First, as a speaker of English or a related language, you may think you know what the word “particle” means. By contrast, you’re probably sure that you don’t know what “wavicle” means. And that’s a good thing! Since electrons’ and photons’ properties are quite unfamiliar, it’s better to bring as few preconceptions along as possible when one first seeks to understand them.
- Second, the word “wavicle” suggests that electrons and photons are more like waves than like dots. That’s true, and important, as we’ll see both today and in the next couple of posts.
Normally the word “particle” in English refers to a little ball or grain, such as a particle of sand or dust, and so an English speaker is imediately tempted to imagine an “elementary particle” as though it were roughly the same thing, only insanely small. But that’s not what electrons are like.
Wavicles are different from particles in several ways, but perhaps the most striking is this: The behavior and the energy of a wavicle are far more sensitive to the wavicle’s surroundings than would be the case for an ordinary particle. That is certainly true of electrons, photons and quarks. Let me show you what I mean.
Side Remark: Is the word “wavicle” really needed?
[An aside: Some might complain that the word “wavicle” is unnecessary. For example, one might propose to use “quantum particle” instead. I’m not convinced that’s any clearer. One could also just use the word “quantum”, the name that Einstein initially suggested. That potentially causes problems, because any vibration, not just waves, may be made from quanta. Well, terminology is always subject to debate; we can discuss this further in the comments if you like.]
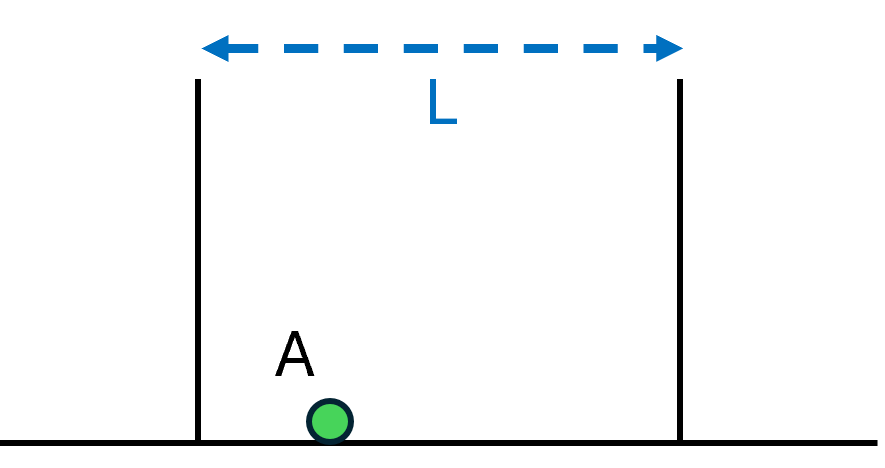
A Stationary Particle in a Constrained Space
Let’s imagine a flat surface bounded by two walls a distance L apart, as in Fig. 1, and place a particle at point A, leaving it stationary. Since the particle is sitting on the ground and isn’t moving, it has the lowest energy it can possibly have.
Why does the particle have its lowest possible energy?
- It’s stationary. If it were to start to move, it would then have additional motion energy.
- It’s at the lowest possible point. If it were lifted up, it would have more energy stored: if it were then released, gravity would convert that stored energy to motion-energy.
How much energy does it have? It has only its internal energy E=mc2, where m is the particle’s mass (specifically, its rest mass), and c is the cosmic speed limit, often called “the speed of light”.
Notice that the particle’s energy doesn’t depend on how far apart the walls are. If we doubled or halved the distance L between the walls, the particle wouldn’t care; it would still have the same energy.
The energy also doesn’t depend on the particle’s distance from the wall. If we placed the particle at point B instead, it would have the same energy. In fact there are an infinite number of places to put the particle that will all have this same, minimal amount of energy.
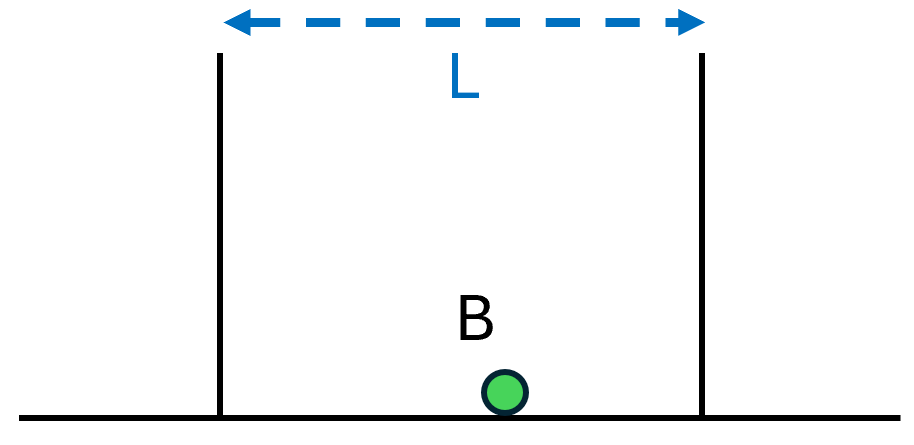
Such are the properties of a stationary particle. It has a location. It has an energy, which depends only on its local environment and not on, say, faraway walls.
Side Remark: Doesn’t gravity from the walls affect the particle and its energy?
Yes, it does, so my statements above are not exactly true. To be pedantic yet again: the walls have extremely tiny gravitational effects on the particle that do depend on the particle’s location and the distance L. But I have a more important point to make that is independent of these effects, so I’m going to ignore them.
Side Remark: Can all this about “lowest possible energy” really be true? Aren’t speed and energy perspective-dependent?
Total energy, like speed, is indeed a relative concept. So to be pedantically precise: the particle isn’t moving relative to us, and therefore, from our perspective, it has the lowest energy it can possibly have. That’s enough for today; we’ll be sticking with our own perspective throughout this post.
A Standing Wave in a Constrained Space
Waves, in contrast to tiny particles, are often exceedingly sensitive to their size and shape of their containers.
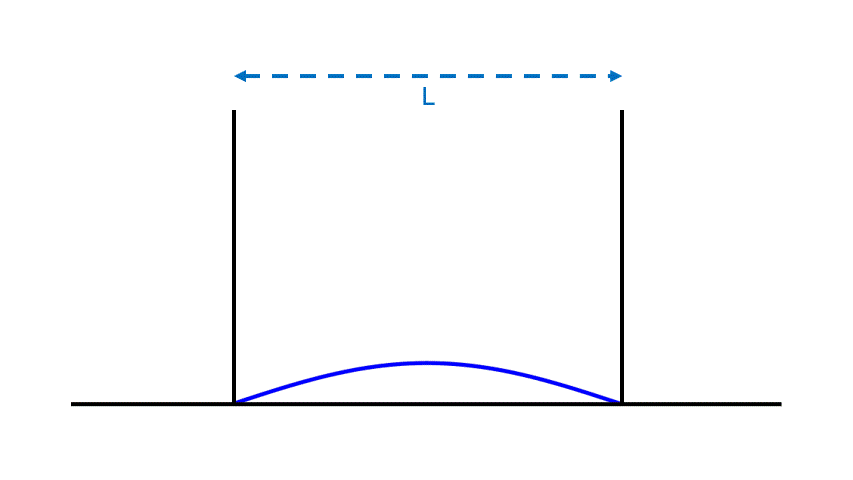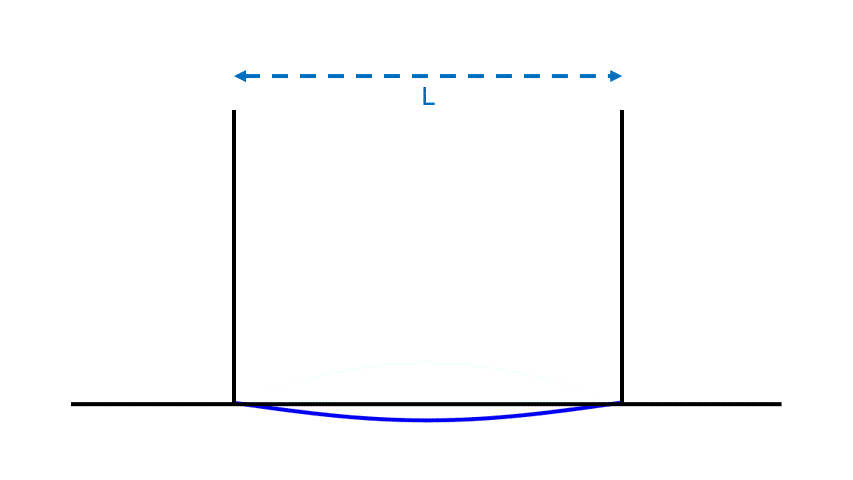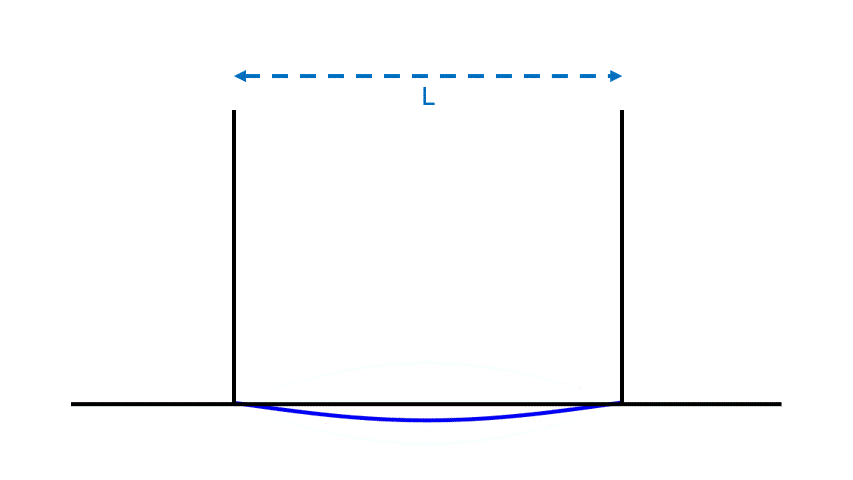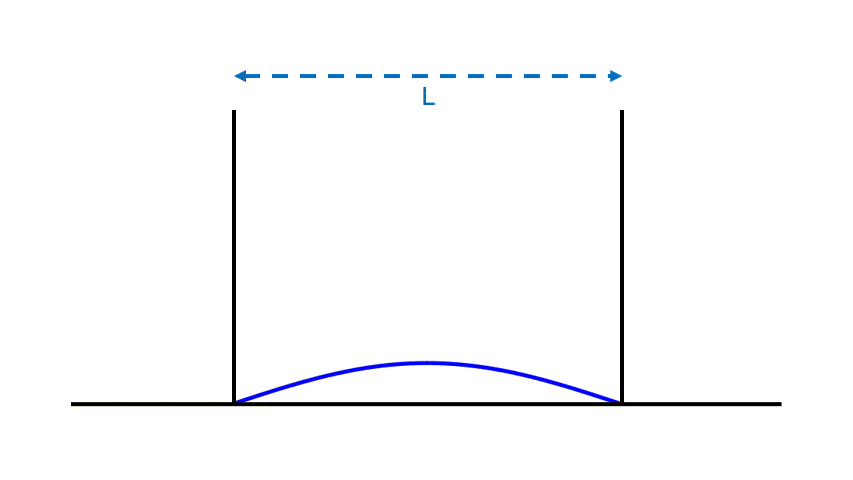
Although we often encounter waves that travel from place to place — ocean waves, earthquake waves, and light waves in empty space — there also stationary waves, known as standing waves, that don’t go anywhere. They stand still, just waving in place, going through a cycle of up-and-down-and-up-again over and over. A famous example of a standing wave would be that on a plucked string, sketched in Fig. 3.

The number of cycles performed by the wave each second is called its frequency. Crucially, if the string’s length is shortened, the frequency of the string’s vibration increases. (This is the principle behind playing guitars, violins, and similar instruments, which play higher musical notes, at higher frequencies, when their strings are made shorter.) In short, the standing wave on a string is sensitive to the length of the string.
More generally, a standing wave has several important properties:
- It has a frequency; the number of back-and-forth cycles per second. In general, if the wave’s container grows wider, the frequency decreases.
- It has a wavelength — the distance between highpoints on the wave — which will increase if the container widens. (I won’t discuss wavelength here, as it doesn’t play a role in what follows.)
- It has an amplitude (or “height”) — which describes how far the wave extends away from its midpoint during each cycle. Unlike frequency and wavelength, which are determined in part by the container’s size, the amplitude is independent of the container and is adjustable. For instance, for the string in Fig. 3, the amplitude (the vibrating string’s maximum extension in the vertical direction) depends on how firmly the string was plucked, not on the string’s length.
For instance, if we take the two walls of Fig. 1 a distance L apart, and we put a simple standing wave there, we will find that the frequency decreases with L, the wavelength increases with L, and the amplitude and energy depend on how “high” the wave is, which has nothing to do with L.
Unlike particles, waves have neither a definite location nor a determined energy.
- A standing wave has no definite location; it is inevitably spread out.
- A standing wave has an adjustable energy; if one increases or decreases the wave’s amplitude, its energy will similarly increase or decrease. (For instance, plucking a guitar string harder puts more energy into the vibration of the string, and leads to a standing wave with a larger amplitude and energy — one which will in turn create a louder sound.)
Particles, meanwhile, have neither frequency, amplitude nor wavelength.
A Standing Wavicle in a Constrained Space
Wavicles differ from both waves and particles. Like a wave, a wavicle is spread out, and can have a definite frequency, unlike a particle. But unlike a wave, a wavicle’s amplitude and energy are not adjustable, and so, like a particle, it can have a definite, fixed energy.
In particular, thanks to a formula that Max Planck guessed and Albert Einstein correctly reinterpreted, a wavicle’s energy and frequency are precisely proportional; if you know one, you know the other. The formula?
- E = f h
where E is the wavicle’s energy, f its frequency, and h is called Planck’s constant. (I sometimes refer to this constant as the cosmic certainty limit, in parallel to c being the cosmic speed limit; but that’s a personal quirk of mine.)
Photons, electrons and quarks are all wavicles, and they share many properties. There is, however, a crucial difference between them: the rest mass of a photon is zero, while that of an electron or quark is positive. This difference affects how their frequency and energy depend on L when they form standing waves in a box. (The differences between the standing waves for these two types of wavicles are shown in this article.)
Let’s look at photons first, and then at electrons.
Photon in a Box
If a photon is trapped in a box, forming a standing wave much like a standing wave on a guitar string, then the minimum frequency of that photon is set by the size of the box L and the cosmic speed limit:
- f = c / L
(Here I’m slightly over-simplifying; since the box is really three-dimensional, not one-dimensional as I’ve drawn it, the formula is slightly more elaborate. See below for the more complete math formulas if you want them.)
But the energy of the photon is also determined, because of the formula E = f h, which implies
- E = h c / L
Therefore, as L shrinks, E rises: the smaller the box, the larger the frequency and energy of the photon.
If the box’s size goes to infinity, the photon’s frequency and energy both go to zero. This reflects the fact that light on its own, isolated from other objects such as a box, cannot form a standing wave. In empty space, light and the photons that make it up are always traveling waves; they can only stand when inside a container.
Click here for more complete formulas for a photon in a box
A three-dimensional, the box has a length, width and height , and the photon’s frequency is
If the box is a cube with sides of equal length , then
The relation is still true, so
I claimed earlier that the energy of a wave is adjustable, while that of a wavicle is not. In this context, that means that the energy of a laser beam can be adjusted, but the energy of the individual photons that make up the laser beam cannot be. How does this work?
Let’s combine N photons of frequency f together. Then we get a wave of frequency f, with energy N times larger than that of a single photon.
- E = N f h
And thus, by adjusting N, making the wave’s amplitude larger, we can adjust the energy E if the wave. (How big might N be? HUGE. If you turn a laser pointer on for one second, the wave emitted by the pointer will typically have N somewhere in the range of a million billion or more.)
By contrast, a single photon corresponds to N = 1. Nothing else can be adjusted; if the photon has frequency f, its energy is fixed to be f h. That energy cannot be changed without also changing f.
Electron in a Box
An electron, unlike a photon, can be a standing wave (and thus stationary) even outside a box. This is a point I emphasized in this post, where I described a type of standing wave that can exist without walls, i.e., without a container.
Such an electron, sitting still and isolated out in empty space, has energy
- E = mc2
where m is the electron’s mass. But since it is a wavicle, E = f h; and so [as discussed further in the book, chapter 17] its frequency is
- f = E / h = m c2 / h
Again, the idea that an electron has a frequency makes sense only because it is a wavicle; were it really a particle, we would be hard pressed to understand why it would have a frequency.
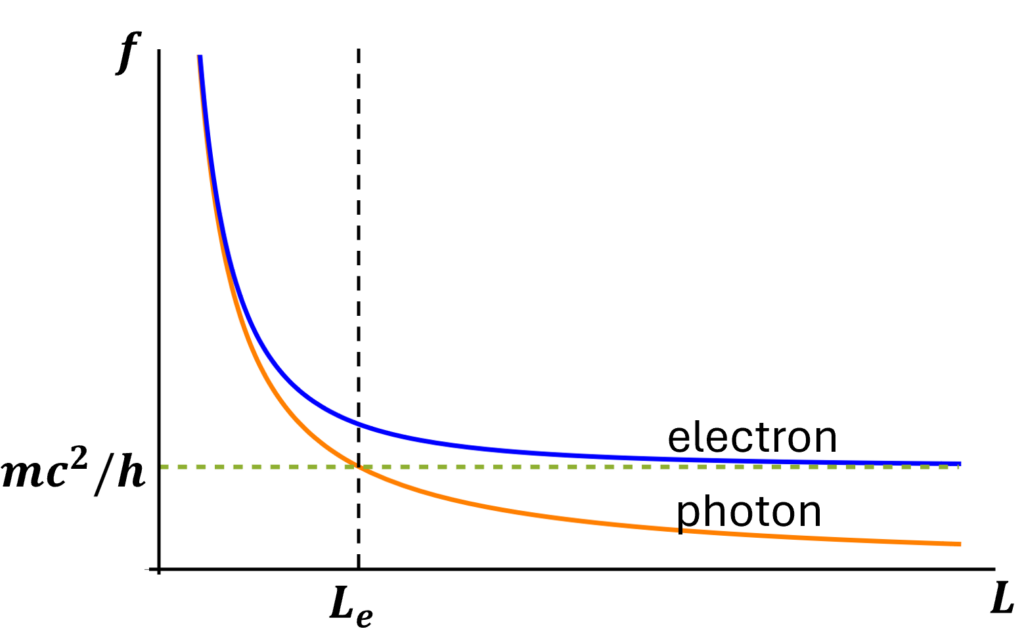
When the electron is placed inside a box of length L, its energy and frequency increase, just as is the case for a photon. However, whether the increase is large or small depends on whether the box is larger or smaller than a certain length, known as the electron’s Compton wavelength Le . That length is
- Le = h / m c = 2 x 10-12 meters
This distance is much smaller than an atom but much larger than a proton or neutron; specifically, it is about a hundredth of the radius of an atom, and about a thousand times larger than the radius of a proton.
Much depends upon the relation between L and Le.
- In a small box, where L is much less than Le , the effect of the box on the electron’s frequency and energy can be very large. In particular, it can make E much bigger than mc2 !!
- In a large box, where L is much greater than Le, then E will be only slightly bigger than mc2.
This behavior of the frequency (and thus the energy) of an electron, as a function of L, is shown in Fig. 5, along with the different behavior of the frequency for a photon. (These two types of behavior of frequency as a function of box size were also shown in this article.) We’ll come back to this in a later post, when we see how it is relevant for atoms.
Click here for the more complete formulas for an electron in a box
Compare the following with the complete formulas for a photon, given above. The electron’s frequency in a box whose sides have different lengths is
If the box is a cube whose sides have equal length , then
The relation is still true, so
Thus if , then
is very slightly larger than
, whereas if
then
, just as for a photon.
Something similar is true for the up and down quarks, and indeed for any “elementary particle” that has a non-zero rest mass. This has relevance for protons and neutrons, a point to be addressed in a later post.
One last point about electrons. If the box is huge — if L is much, much greater than Le — then the electron can exist for a very long time as a localized standing wave, occupying only a small part of its box. This allows it to behave more like the particle in Fig. 1, tightly localized at a point, than like the wave of Fig. 4, which entirely fills the box. (Again, see this post on unfamiliar standing waves.) In that circumstance, the electron won’t have the lowest energy it can possibly have — to reach that low enerrgy would require filling the entire box — but its energy will still exceed mc2 by only a minuscule amount.
This illustrates another crucial fact: wavicles with rest mass can sometimes be much more particle-like than wavicles without rest mass, with an approximate location as well as an almost definite energy. It’s another reason why scientists initially thought electrons were particles (in the usual sense of the word) and were slow to understand their wave-like properties.
A Comparison
To sum up, particles don’t have frequency, and waves don’t have their energy tied to their frequency; it’s having both frequency and specific associated energy that makes wavicles special. A key feature of a wavicle is that when you make it stationary and put it in a box, its frequency and energy generally increase; the smaller the box, the greater the effect. As seen in Fig. 5, the increase is particularly dramatic if the box is comparable to or smaller than the particle’s Compton wavelength.
To help you remember the differences, here’s a table summarizing the properties of these objects.
| stationary particle | standing wave | standing wavicle | |
| location | definite | indefinite | indefinite |
| energy | definite, container-independent | adjustable | definite, fixed by frequency |
| frequency | none | container-dependent | container-dependent |
| amplitude | none | adjustable | fixed by frequency & container |
A stationary particle, standing wave, and standing wavicle, placed in an identical constrained space and with the lowest possible energy that they can have, exhibit quite different properties.
The Old and New(er) Quantum Physics
Niels Bohr was one of the twentieth century’s greatest physicists and one of the founders of quantum physics. Back in the late 1920s and early 1930s, in his attempt to make sense of the confusions that quantum physics generated among the experts, he declared that electrons are both wave and particle — that depending upon context, sometimes one must view an electron as a wave, and sometimes one must view it as a particle. (This “wave-particle duality” lies at the heart of what came to be called the “Copenhagen interpretation of quantum physics.”)
But this was back in the days before quantum field theory, when quantum physics was very new. The quantum theory of the 1920s did indeed treat electrons as particles — with positions, yet described by a wave-function. It didn’t treat photons in the same way. It was only later, in the middle of the century, that quantum field theory came along. Quantum field theory put electrons and photons on exactly the same footing, treating both as wavicles, described by a single, overall wave-function. (Important! be sure not to confuse wavicles with the wave-function; they are completely different beasts!!)
This quantum field theory viewpoint didn’t really fit with Bohr’s vision. But it’s quantum field theory that agrees with experiment, not the quantum physics of Bohr’s era. Nevertheless, Bohr’s interpretation persisted (and still persists) in many textbooks and philosophy books. I learned about it myself at the age of sixteen in a class on the philosophy of science. That was several years before I learned the mathematics of quantum field theory and began to question Bohr’s thinking.
From the perspective of quantum field theory, as I’ve outlined here, a wavicle does have features of both waves and particles, but it also lacks features of both waves and particles. For this reason, I would personally prefer to say that it is neither one. I don’t think it’s useful to say that it is both wave and particle, or to say that it is sometimes wave and sometimes particle. It’s simply something else.
But this is something we could debate, and perhaps some readers will disagree with me. I’m happy to discuss this in the comments.
That said, however, I do want to emphasize strongly that using “wavicle” does not in any way help resolve the most confusing issues with quantum physics. Adopting “wavicle” does not make it any easier to understand, for instance, the quantum double slit experiment or the issue of entanglement’s “spooky action at a distance”. I do think quantum field theory has the advantage of removing certain unnecessary confusions, making it somewhat easier to state the problems of quantum physics. But this makes them no easier to resolve.
Such issues, however, are a topic for another time.



51 Responses
What are the practical differences between a wavicle and a particle bouncing back and forth between the walls, rather than just sitting there?
Well, there are many possible answers to that question. Here is one: a particle could only follow a single path at once, whereas a wavicle could be moving in multiple directions and be bouncing of the left and right walls simultaneously (see the first plot, left hand side, of https://profmattstrassler.com/2024/03/19/yes-standing-waves-can-exist-without-walls/) , or off the ceiling and the front simultaneously. So the wavicle has many more things that it can do. This can be used in quantum experiments and technology.
Ah, that was interesting! If a density matrix allows for local measurements (with reduced matrixes) then that seem to work for me if observation is relativistically consistent. (As we discussed earlier, “Answering Mermin’s challenge…”.) I rather have general relativistic patches with different vacua, which is what I thought the S matrix allowed.
[Since the interaction picture with its density matrixes is also consistent with unitarity I expect that physics carries over to it if it most generally applies for Feynman path integrals, but perhaps not always cleanly so. With phase transitions and possibly permanent domain walls in between the different vacua AFAIU.]
But as you say, that’s my internal discussion, not something to discuss here.
https://www.nature.com/articles/s41598-020-72817-7
Stuckey, W.M., Silberstein, M., McDevitt, T. et al. Answering Mermin’s challenge with conservation per no preferred reference frame. Sci Rep 10, 15771 (2020). https://doi.org/10.1038/s41598-020-72817-7
You have already responded that it takes too much time to read it. And that is all right, my own time has been taken so I haven’t responded post haste.
I should add, if you think the Born rule doesn’t carry over to QFT, that it is relativity that enforces it. (But not to ensure a cosmic speed limit but a cosmic spin state. YMMV.)
How does string theory fit into this wavicle picture?
It seems that strings (1 dimensional particles) are a step back to “ordinary” QM and that the superior string theory abandons the field aspect of QFT.
String theory itself isn’t a step back to QM; just the most common technical approaches to calculation are. String field theory exists and is a generalization of field theory, but it is hard to work with.
Even in particle physics, you can formulate many calculations in QFT in terms of a sort of QM if you want; in fact that’s what I did for my Ph.D. thesis. But again, that’s a technical point, not a conceptual one. You start with QFT as the basic definition of the theory, you derive what you want to calculate, and then you rewrite it as a QM-like problem.
Note also that in both particle and string physics, when you use this QM-like approach, your time coordinate is proper time, not universal time. You’re not literally going back to quantum mechanics; you have a fully relativistic theory, and you are treating photons and electrons on the same footing, which is not true for 1920s quantum mechanics.
So if you see how this works in QFT, then it becomes clear how it works in string theory — and it is very much parallel.
I almost forgot:
“The electron’s frequency in a box whose sides have different lengths L_x, L_y, L_z is
f = \sqrt{(mc^2/h)^2+ c^2/L_x^2 + c^2/L_y^2+c^2/L_z^2}”
I think you mean f = 1/\sqrt{(mc^2/h)^2+ c^2/L_x^2 + c^2/L_y^2+c^2/L_z^2} here.
Not so; when L is infinite, frequency is proportional to mass, and as L goes to zero, frequency goes to infinity.
How should I think about mass distribution in a field? I had first year QM in college, but have not thought about it much until I ran across your posts. (And I have a copy of your book that I’ve started.)
I expect the mass to appear distributed across the field based on probabilities of finding a particle based on the wave (rather the wave squared). Are there experiments that show mass distributed in this way? I’m expecting not since gravity is so weak. However mass appears in many other ways than gravitational force.
I might be confusing wavicle and wave function here?
Yes, you are in danger of that… of confusing field and wave function. when you say, “I expect the mass to appear distributed across the field based on probabilities of finding a particle based on the wave (rather the wave squared)”, you have the wrong expectation, because you’re thinking of a field as related to a wave function, and having something to do with probability. This isn’t the case.
Classical fields are just what you learned in first-year physics: the electric field, for instance. It’s a vector at each point in space. The wave function in a field theory is a function that tells you the probability that the field takes on a particular shape. There are an infinite number of possible shapes for the electric field, each one itself described by three functions . The wave function is then a function of this function,
. The wave function is then a function of this function, ![\Psi[\vec E(x,y,z)]](https://s0.wp.com/latex.php?latex=%5CPsi%5B%5Cvec+E%28x%2Cy%2Cz%29%5D&bg=ffffff&fg=000&s=0&c=20201002) — it is not a function of space, but a function of three functions on space.
— it is not a function of space, but a function of three functions on space.
The space of functions is infinite dimensional — for instance, it takes an infinite number of Fourier coefficients to specify a function. Therefore the wave function is a function on an infinite dimensional space: the probabilities it specifies are not in ordinary three-dimensional space, but rather in the gigantic space of all possibilities.
When it comes to mass distributions in a particular quantum state of a field, the wave function does not tell you the mass distribution, but rather the probability that the field has a particular mass distribution, as opposed to some other one. Just as a wave function of a particle tells you the probability of finding the particle in this place or that when you do a measurement, the wave function of a field tells you the probability of finding it taking this shape or that shape when you do a measurement. The mass distribution depends on the field’s shape (and how it’s changing, too, so it’s a bit more complicated than I’ve made it sound.)
If the field were classical, then you could specify its shape and talk about distributions in, say, energy and momentum. But it’s quantum, so its shape is not unique and, in any given state, is described by this above-mentioned huge wave function.
And sure, any quantum experiment on fields — even the standard double-slit experiment — shows this is true.
In some specific states, the mass distribution may be more or less known. For example, if I set up an empty room with a salt crystal in it, the salt crystal (and its possible mass distributions) is described by a wave function that only has probability for the corresponding fields to form something like a salt crystal in something like that location. So then all the parts of the wave function have the mass distribution corresponding, approximately, to that of a salt crystal.
But this is a non-generic situation in field theory. In general the wave function represents a superposition of many different field configurations with many different mass distributions. Averages won’t help. Just as the average position of a particle may not have any probability at all (as when a particle in a double well has an average position at zero, but spends no time there), the same is true for fields; the average mass distribution may be a distribution that no part of the wave function actually realizes.
p.s. even though this does not address field theory in a quantitative and precise way, it may help you build more intuition. https://profmattstrassler.com/articles-and-posts/particle-physics-basics/fields-and-their-particles-with-math/
While we wait for an expert answer, I note that field fluctuations (and by extension, I assume wavicles) do seem to have mass energy distributions, implying that you may be on the correct track.
This because it is widely accepted that the cosmic filaments of gas and galaxies ultimately derives from fluctuations in the inflaton field, as do the related imprints in the cosmic microwave background. [Related description of current research in simple format here: https://www.youtube.com/watch?v=OHdUFPAK7f0&ab_channel=SixtySymbols .] The mass energy fluctuations translates to (radiation and) gas density and momentum fluctuations during the hot big bang, which in turn breaks as caustics and become affected by gravity so produce a filament like “cosmic web” (of mostly dark matter). The first part agrees with (inflation and) cosmic background observations, the latter part agrees with cosmological simulations that agree with observations.
Torbjorn’s reply on this matter adds another layer of complexity to the question: if there is only one wave function of the universe and it covers many possible shapes for the fields and spacetime, how come we only see one? The answer is that we’re inside the wave function, and quantum physics, while not predicting which world we will observe, predicts that we will observe at most one.
I didn’t mean to add complexity. Here I thought the “wavefunction of the universe” was questioned as to make sense, since it e.g. suggests many-world theory and in the Wheeler–DeWitt form doesn’t include time?
In more practical terms, the inflation fluctuations happens in a general relativity setting, so there is only one spacetime to work with (unless we want to contemplate quantum gravity, which is another bag of Schrödinger’s cats).
The wave function of the universe is a controversial notion, sure, but if you want a continuous equation for the whole universe that has a consistent set of solutions, that’s the only option you have (so far.) (A density matrix might also be considered instead, but that’s way off topic.)
I think one thing that makes me a bit reluctant to use a term like “wavicle” in popularization is that it makes it hard to distinguish the “quantum” part from the “field theory” part. That is, I kind of want to be able to say something like “this is how a particle/field behaves in classical physics, this is how it behaves in quantum physics”. But this may just not be a good thing to try to do in general, certainly a persistent message from “wise QFT folks” is that past a certain point you can’t really separate these things.
I’m not sure what you mean. Classical field theory has waves. There is no relation E = h f that fixes the energy of a wave; you can make it whatever you like. It’s just like any wave that you’re familiar with: the water waves, sound waves, and waves on fabric or string that we’ve all experienced.
Quantum field theory has wavicles, out of which its waves are built. For wavicles, the relation E = h f applies, and the amplitude and energy of a such a wave is not adjustable. Such a thing is never encountered (consciously) in ordinary experience.
It seems hard for to imagine that one could confuse these two things; one is perfectly familiar and intuitive, the other completely bizarre and counter-intuitive.
I guess one way to say it is that I find it more useful to describe moving from classical to quantum as a change in how observations and dynamics work rather than a change in what kinds of objects exist. In part, because it makes it a bit easier to talk about QM and QFT in the same context, as quantum theories that modify their classical counterparts in related ways by changing how we talk about the particles/waves respectively in those theories.
I don’t think what you’re doing is incorrect or anything, it helps you state certain kinds of things clearly (especially when you’re focused specifically on describing QFT, as you were in the book). I’m just not sure that it’s something I could use consistently, because it feels like there are certain kinds of things I’d like to talk about that are harder to talk about in that language. But as mentioned above, it may be that the kinds of things I want to say are misleading, and not being able to say them as easy is an advantage. 😛
I’m actually not disaagreeing with you about that. Wavicles are not a panacea or a global phenomenon that you have to talk about (in contrast to wave functions or Hilbert spaces, which are part of the structure of quantum theory.)
But when you’re going from classical to quantum, you need to do it correctly.
Classical, non-relativistic particles become the quantum physics of 1920s. There are no wavicles there. That’s all fine, as long as you remember that’s only an approximation to the world. [and as long as you make clear what multiparticle wave functions are and aren’t.]
You can also learn a lot from coupled spins that have no other motion across space. Those aren’t wavicles either… and if the spin is large, there’s a classical limit that you can compare to.
However, classical relativistic particles can only be described using field theory; nothing else is consistent. Classical fields and their waves become quantum fields and their wavicles. There isn’t any real alternative, at least not an easy one. (When people say “second quantization”, or confuse fields and some notion of quantized wave-functions, they’ve usually misunderstood how field theory works.)
This is the real world, in the sense that quantum field theory provides the only description of nature that even comes close to explaining how the cosmos works. That’s why “wavicle” is such an important term — not that it takes over for the classical-quantum transition, but that wavicles are the fundamental ingredients out of which we and everything around us are made, according to current theory.
It’s easy to combine the particle and wavicle discussions. You start with 1920s quantum physics and its classical antecedent. Then you build a string out of a set of particles coupled by identical springs, taking the number of balls and springs to be fairly big, or even infinite. Do this both classically and quantum mechanically, and you’ll see exactly how waves emerge in the classical regime and wavicles emerge in the quantum regime, even though you built the whole thing from particles — it’s just the harmonic oscillator all over again.
So I’m not suggesting that you should use the term “wavicle” as some sort of general quantum notion. Wavicles are specific; they are the quanta of waves, so if you don’t have waves in the classical regime, you may not have wavicles. [That said, electrons and other fermionic “particles” are wavicles, but have no classical limit. And some interacting quantum field theories may not have wavicles (cf. “conformal field theory.”) So there isn’t some entirely general story for wavicles either; there’s lots of nuance and detail. ]
p.s. I’m hardly out on a limb here. Nobel Prize winner Frank Wilczek uses “wavicles” in popularization; I learned it from him. Neil de Grasse Tyson uses it, hardly a slouch when it comes to popularization. Before publication, my book was read by a number of famous physicists (Nima Arkani-Hamed [Breakthrough Prize], Martin Rees [Royal Astronomer], Michael Peskin [Author of the most popular quantum field theory book of its day]) and not only did they endorse the book, not one of them raised a question with me about the use of “Wavicle”. Nor has anyone among my colleagues since the book came out.
Two questions on this.
In Pilot Wave Theory, is th particle involved seen as a ‘true’ particle, with no wavelength and a definite location?
Second, if we drop an electron into a large box, you say its energy will lower as it fills the whole box. I assume this will involve the emission of photons? Does this mean that an electron ejected from nay confinement to ’empty space’ will emit energy? Is this a known or observed effect?
Question 1: note my answer to Anthony Way above, it is somewhat relevant. Yes, in pilot wave theory, the electron is a particle, not a wavicle. But this gets uglier when you are trying to discuss multiple particles at once, and worse, particles that can be created or destroyed, and I’ve never seen that clarified.
I have also never seen a treatment of Pilot Wave Quantum Field Theory, nor have I ever been able to imagine how it would work for an interacting field, or how it would be useful. In such a theory, there would be a field with a definite value everywhere, and a wave moving in an infinite dimensional space that guides it. Somehow this would have to be constructed for multiple, interacting fields located in a potentially curved spacetime. Moreover, all this would have to be done while preserving known symmetries of quantum field theory, which often tell you that a physical system can be described using two different sets of fields or even different spacetimes. I have no idea how you would construct Pilot Wave QFT to satisfy all those criteria, and I’m deeply skeptical that it would be possible.
Without a complete proposal, I don’t see the point in the pilot wave approach. Maybe pilot wave thinking can make one feel better about particles moving according to an uncertainty principle. But we know that quantum mechanics, for which pilot wave theory was developed, is not a complete theory of nature. No one has given any argument, to my knowledge, as to why a pilot wave approach to QFT would both make us feel better about fields and uncertainty and preserve all the excellent properties of standard QFT. In fact I can think of many nice properties of QFT that a pilot wave approach would break.
In that negative context, it would still be possible to study how pilot wave approaches treat wavicles by using quantum mechanics itself to build a quantum field theory of phonons on a lattice. I don’t think it would be hard, but it would be time-consuming.
Question 2: If the electron moves from one state with energy E1 to another state with lower energy E2, then the extra energy will be dissipated somehow. There are often multiple options for how the dissipation occurs, but for electrons, photon emission is usually the quickest and easiest way. And yes, it is regularly observed. Indeed one can understand the emission of photons as an electron goes from a highly excited state in an atom down to the ground state as an example of this very phenomenon. Other examples can be observed in artificial contexts, such as quantum dots.
However, the way you phrased your final question was confusing. “Does this mean that an electron ejected from any confinement to ’empty space’ will emit energy? Is this a known or observed effect?” Here you are conflating multiple steps (and I did some of this in the post, to keep it shorter.)
First, something has to provide energy to the electron so that it can be ejected. In the example here, something has to squeeze the box, and that takes energy, some of which is transferred to the electron.
Second, the electron has to find a way to move from a state inside the box to a state that is no longer within the box. This requires the electron interact with something, perhaps just atoms in the walls of the box, or perhaps with an incoming photon if the box is transparent to light. The new state may not be the lowest energy state available to the electron, but it will have slightly lower energy than the first one, and so, yes, something will have to carry off the excess energy. That could be an emitted photon. But the energy could also be absorbed by atoms of the box, or by the atoms in the floor and walls outside the box.
Third, the now-escaped electron probably has more energy than the ground state of an electron outside the box. For it to become stationary, it must lose that excess energy. It can lose that energy as it interacts with walls and other objects outside the box, causing a garden-variety form of dissipation in which photons will often be emitted; this is a particle-physics form of friction, in which interactions bring the electron to a standstill. It only works if there’s enough stuff around for the electron to interact with, and it may take a long time; and if L is infinite, the electron may instead just wander off and never come to a standstill, still carrying that excess energy.
So you see there are a lot of mildly interesting details hidden under the hood — necessarily hidden, in order to make the main point of the post in a succinct fashion.
I can see my second question was poorly written. To be more specific, we saw in earlier posts that an electron whose box vanishes will not immediately rush off at light speed to fill all the available space. It is a ‘standing wave’ that doesn’t need walls.
What say then that I take an electron in a box and remove\enlarge that box. Can I do this in a way that the box is removed faster than the electron standing wave can propogate through space, so that at some point the electron is no longer interacting with the box or anything else external, but has not yet filled all possible space in whatever larger box it may find itself in?
An electron in a larger box has a lower energy, so one moving from a small to larger box must release that energy somehow. But is it bound to do so only by interaction with the box or can it, ‘by itself’ release energy as its spreads to fill a sufficiently large box?
For the second paragraph, yes, you can move the edges of the box at any speed up to light speed, while the electron will spread out at a speed that you can guess from Newtonian analogues to quantum physics. If the box is much larger to start with than the electron’s Compton wavelength, then the excess energy of the electron, relative to mc^2, is small, and it is nothing but the quantum analogue to 1/2 mv^2. (If the box is smaller instead, then you need a relativistic version of this conversation, but that’s much more complicated.) That “v” speed tells you how quickly the electron will spread out. How fast is v? If the box is large, then the energy of the electron minus mc^2 is approximately h^2 / (2 m L^2), and so v = h / m L [and so v/c = h/(mcL) = L_e / L.] This is just the uncertainty principle all over again, which a single wavicle automatically satisfies.
Now, if you make the box much larger or take the box away altogether, then the **ground state** energy of the electron decreases… i.e., the lowest possible energy that the electron can have. But that by itself doesn’t necessarily reduce the energy of the electron. Depending on what the electron can interact with, it will lose energy by emitting photons. For example, if the box is large but still nearby, then at some point the electron will interact with the box, at which point it can emit photons and start losing its excess energy. If the box is infinite and the electron has nothing to interact with, however, then energy-momentum conservation may assure that it keeps its energy — a spreading-out electron may continue to spread out indefinitely, and has more energy than an electron which fills the entire box — in this case, the entire universe.
Note that the excess energy may be extremely tiny!! The excess energy is 1/2 mc^2* (L_e/L)^2, so if the box is a meter across, the excess energy is of order 10^{-24} of the electron’s mc^2, or less than 10^{-18} eV. That’s why this really doesn’t matter; at macroscopic scales, you’d never observe the photon emitted in this process.
First, you are a master of explaining the near inexplainable. It is a pleasure to be drawn back into a re-reading of your thoughts.
Second, I am trying to reconcile your Wavicle Interpretation with Ruth Kastner’s Transactional Interpretation so let me pose an observation. If a wavicle had a simultaneously defined position and movement (momentum) then it would also have a definite path (continuous trajectory) thru space-time from here to there. But, since a wavicle does not have both a simultaneous position and momentum, does this suggest that wavicles also do not traverse a continuous trajectory at least in space-time?
Thanks for your kind remarks! Hopefully I can live up to them today.
The whole tenor of your question, and the assumptions behind it, are very pre-quantum-field-theory.
You are still treating position and momentum as though they are on the same footing. That is largely true in quantum mechanics, where one ignores special relativity, treats an electron as an object whose properties are position and momentum, and skirts the issue of photons. It is somewhat less true in quantum field theory, where the basic objects are fields, and whatever answer one gives has to hold at very high energy where any masses are irrelevant.
In pre-quantum physics, a wave in a field, such as a sound wave, never has a trajectory, and we don’t expect it to. In quantum field theory, a wavicle never has a trajectory either. It can only have an approximate one. That’s just the starting point, independent of any interpretations we might then impose on how to think about how quantum physics works. The main difference between a wave and a wavicle is that the latter has a normalization condition — given its shape, you can’t arbitrarily increase or decrease its amplitude. It’s not that the former has no trajectory and the latter has one.
You asked “does this suggest that wavicles also do not traverse a continuous trajectory at least in space-time?” This can be interpreted two ways and I’m not sure which one you meant. Are you focused on the question as to whether it might have a discontinuous trajectory? or on whether it has no trajectory at all? Either way, I would say the question is moot; a wavicle does not have a trajectory, and can only have an approximate trajectory, and even then, only if it has rest mass or is trapped in something like an optical fiber. This is directly related to my recent discussion about standing waves of two types: see https://profmattstrassler.com/2024/03/19/yes-standing-waves-can-exist-without-walls and the posts that it links to. I point out there (and in the book) that a stationary electron is a standing wave; this just follows from the equations of quantum field theory. Generally, as one can work out with simple mathematics, an electron can be microscopically delocalized (spread out by much more than a bacterium) but still macroscopically localized (much smaller than a millimeter.) Now, if the electron is stationary relative to you, and if I travel smoothly past you, I will see the electron moving on a (straight) trajectory. But that trajectory is, again, macroscopically localized but microscopically delocalized. If we try to localize the trajectory to something truly atomic size or smaller, the electron wavicle will resist our efforts to do so. (See today’s post.)
The same is true of a photon in an optical fiber. On the macroscopic scale, there’s no question the photon travels in and along the fiber. But on the scale of the fiber, it is spread out.
So I do not think I have answered your question, but I am not sure that it is the question you should be asking. As for Kastner’s interpretation, I am not very familiar with it, but I don’t think it is relevant to the basic question of what wavicles are. You are again at risk of conflating issues that have to do with wave functions, and probabilities for entire systems, with wavicles, which are little waves in three dimensional space. (https://profmattstrassler.com/2024/04/25/why-a-wave-function-cant-hurt-you ) Quantum mechanics, especially one-particle quantum mechancis, and the extensive philosophical discussion around it, help makes this conflation possible and easy. In my view, quantum field theory makes it clear that one should avoid it.
Could you expand on the role of the Heisenberg Uncertainty Principle in quantum field theory? Are saying that position and momentum do not apply to wavicles or that position and momentum are not mutually exclusive complementary variables?
In QFT the uncertainty principle tells you that the value of a field, and the rate at which the value of field is changing, cannot simultaneously be known. That’s what takes the place of position and momentum.
This does, in turn, affect the properties of wavicles. Nevertheless, it would never occur to a person thinking about waves to ask what a wave’s trajectory is unless one is already in a sort of geometric-optics regime, where waves can be seen to follow a rough path — and even then one would not expect a wave’s trajectory to be perfectly sharp. Knowing that electrons are wavicles, one can similarly stop worrying about why an electron has no definite trajectory; no wave of any sort has such a thing.
Even ordinary waves already have a sort of uncertainty principle built in: you cannot know where a wave is going and where it is simultaneously. Just try to make a big spike in the water; then you know, for a moment, where the spike is, but instantly thereafter it rushes out in all directions. Conversely, if you want to know where a wave is going, make a nice sine wave heading in a definite direction; but then it’s spread out everywhere. Now, this is about position and velocity; but for a wavicle, which has a definite mass unlike a general wave, the relation between velocity and momentum is clear, and so a wavicle has a position-momentum relation in those circumstances where the wavicle’s motion approaches a path.
Now what you’re asking is the relation between the statement in the first paragraph and the statements in the 2nd and 3rd. It is not very direct, and is little discussed. I ought to find a way to make it clearer, so that I can answer your question more precisely; I’ll think about it.
“Hmm” (the sound of me thinking). And I am thinking I need to read WIAIS a second time, for it usually takes me 3 readings to approximate understanding.
But as a parting wondering thought: Since, as you say, the wave-like functions of wavicles are different from ordinary space-time waves might we need to consider domains outside of space-time? Could resolving the conundrums of double slits and entanglement require challenging our universe assumptions, as did Copernicus?
Anyway, I look forward to when you “find a way to make clearer” the relation between uncertainty and trajectories.
Again, there are three types of waves moving around here.
(a) Ordinary waves that we encounter every day in sound and water, part of ordinary life and existing in spacetime.
(b) Wavicles, the gentlest ripples, carrying the lowest energy that a wave of that frequency can have; these are inherently part of quantum physics, but they exist in ordinary spacetime — in fact, certain ordinary waves (including light) are made from wavicles.
(c) “wave functions” also called “probability waves”, which are not themselves physical objects, in contrast to ordinary waves and to wavicles, in that they do not carry energy, electric charge, momentum, etc. — and they do not exist in ordinary spacetime, but rather in the space of possibilities. They are essential, in quantum physics, in describing the behavior of entire systems of objects.
“Could resolving the conundrums of double slits and entanglement require challenging our universe assumptions, as did Copernicus?” The confusions about the double slit experiment — i.e. how does an electron seem to interfere with itself, in a wavelike fashion, and yet manage to collide with only one atom, unlike an ordinary wave which would hit the whole screen at once…? — are very much about (c), not (b). If you treat the screen of atoms as well as the electron through a single wave-function, then the question has an answer, but one that is unsatisfying and drives you inexorably to the Everett “many-worlds” view of quantum physics. If you try to do something else, you get an incomplete description of the physics. Either way, a naive notion that quantum physics describes objects that simply move and interact in spacetime seems clearly too glib. So in that sense we already challenge our “universe assumptions”; many theorists, myself included, expect that space is emergent, not fundamental, and the same may even be true of time.
“If you try to do something else, you get an incomplete description of the physics.”
FWIW: Or you get statistical descriptions (as implied by the Born rule). Which I didn’t like because of the “just so” modeling until I found the relativistic based “conservation per no preferred reference frame” model we have discussed before. That can as well be considered unsatisfying by experts, but if relativistic spin observation effects are as paradoxical as time dilation and length shortening observational effects they seem in principle “satisfying enough”.
Well, Einstein would have argued that a statistical description is incomplete, and I don’t yet see a reason to disagree with him. What’s a reference for the model you’re referring to?
Like you, I find Many-Worlds incomprehendible: A new world every time every wavicle in the universe transfers energy? More comprehendible by me is the pre-space-time and emerging space-time of RE Kastner’s Transactional Interpretation, but I expect that my re-reading of WIAIS will expand my universe understanding even more.
Many thanks!
Well, just to warn you, you won’t find anything about that kind of subject! No Everett, no Bohr, no Kastner, no Rovelli, no Bohm. I very specifically skirted all of the complications of interpretations of quantum physics in this book — because they are BOTH extremely confusing AND almost completely unnecessary for the main points I was trying to make.
My goal in this book is to give you a clear vision of everything else — everything you need to know about the basics of how the universe works *except* for the confusing aspects of quantum physics. A book on that subject would be a many-year project on its own, and I have not even figured out how I would construct it yet.
Re: “just to warn you, you won’t find anything about that kind of subject!”
Sorry, too late, I have already started the re-read. But thanks for the heads up; that better orients my expectations.
I was a little disappointed that you never used the word “wavicle” in your conversation with Sean Carroll. Is there a reason you didn’t? Maybe you use it with laypeople but not physicists?
In general I like wavicle in order to emphasize that everything is waves. An electron is always a wave, a standing wave, that can act like a “particle” in interactions.
Have you tried to use it everywhere, like at physics conferences and talking with your physicist colleagues? Would they be willing to accept wavicle instead of particle?
Thanks for the book, I found a number of interesting concepts in it after contemplating it and your blog posts for a while.
It’s already a couple of months back… so I’m not entirely sure. One reason is that Sean didn’t ask about it, so it didn’t come up. But also, as you note, physicists already use “particle” to mean “wavicle” and, as experts, we all know what we mean. We all know that electrons have E=hf and that the word “particle” is a misnomer, but we stick with it. That doesn’t mean it’s wise, but it’s what we do. So it wasn’t a conversation where either of us felt it was exceptionally necessary, as long as it was clear what “particles” like electrons are actually like — namely, stationary electrons are standing waves.
Now, terminology within a scientific field does not change rapidly, or lightly. For instance, “Higgs boson” is clearly a terrible name; no other particle is named after a person. But attempts to call it the “H boson” has so far failed. Why? Habits built over decades are hard to break. All the existing papers call it the “Higgs boson”. Some people always object to changing terminology, arguing that words don’t have to be perfect when every expert knows what they do and don’t mean. Other people want to call the H boson by some other name. Etc. Someday the terminology may change, but no one person or small group of people make it happen. It is a large-scale sociological shift.
Sean Carroll himself would prefer to call “Dark Energy” by the name “Dark Smooth Tension”. I agree with him. And yet I use the same phraseology as everyone else, because there’s no groundswell of opinion to make the change.
Similarly, if “wavicle” takes over someday, it will not be because I insisted on using it at conferences. Just like all my other colleagues, I have been saying and writing “particle” in physics conferences and papers for three decades and I’m not going to change that overnight. Nor would anyone else. My standing up and beating a drum for this terminology change will have absolutely no effect whatsoever. Frank Wilczek, similarly, uses it in certain contexts, but not in papers or at conferences. Nevertheless, even though Frank made no effort to convince me to use the term, his use of it outside of professional contexts convinced me of its merits, and so I adopted it also. Perhaps in twenty years all the young people, having read my book and Frank’s books, will agree that it is better. But it’s not up to me. And in my view, making a crusade out of it would surely backfire.
Terminology can follow usage (or not), perhaps “wavicle” can shock people out of the QM “duality” frame once in a while.
Re the Higgs field, we do speak of fermion fields so perhaps the higgson field could one day be an acceptable compromise?
I understand the reluctance against the exceptional. But it can also be done en masse, for instance astronomy and biology has no compunction against promoting personal names for object naming. E.g. Kapteyn’s star or the tapeworm Acanthobothrium zimmeri after science popularizer Carl Zimmer.
Matt, this is really great stuff. Thanks for taking the time to do all this. This makes me want to buy your book.
Great! And there’s more to come…
Making things more precise but necessarily complicated, my interpretation of the above is that all of the wavicles making up the box to confine the electron and photon will interact with everything in the system via the force/Boson and matter/Fermion fields. But this can be considerably simplified to a single photon or electron interacting with the walls of the container as you’ve done here. At the very least, the incoming and outgoing photon reflected off a wall isn’t the same as one another?
Yes, if we want a complete description of the enormous number of wavicles that make up the walls of the box, as well as the wavicle inside the box, we will have a much more complicated discussion. But it’s too early to think it over. Hold the thought until after we’ve discussed atoms and protons, probably early next week. Only then can we hope to think about how macroscopic objects work in this language.
I want to make sure my understanding is clear. I like the word wavicle…a lot. I think it makes certain concepts much clearer. Looking at an atom, when an electron jumps from a higher orbital, to a lower orbital, it loses energy by firing off a photon. Howrever, wouldn’t the lower orbital be analogous to a smaller box? Causing the energy to increase? What am I convoluting here?
Unless, we are talking about total energy, in other words, the energy fired off by the electron jumping to a lower energy level, decreases the TOTAL energy, but incurs increased “wavicle” energy being in a smaller box
Similar to how an object changes “orbit” around a massive body, in that it must decrease its TOTAL energy to transition to a lower orbit, although it’s Kinetic energy in the lower orbit is higher.
You are absolutely right on the second try; the effect on the wavicle’s energy is a form of kinetic energy (even though the wavicle may not be going anywhere!). The wavicle gains kinetic energy simply because the box is smaller. But there can be other sources of energy, such as that of electric attraction, which counter this; that’s what happens in an atom.
More on this in coming days.
Joseph, your orbit example is good in that the electron drops further into the “energy well” of the nucleus, which is the “same” in that the object drops further into the “gravity well” of the massive body.
That’s right, and there will be a more precise discussion of this coming up soon.
I like the terminology “wavicle”. Sometimes analogies lose relevance, and you must simply learn a new idea. This happens in language translation: Sometimes the best approach is to force your reader to learn a new word in the foreign language rather than suffer a poor translation.
I agree that this is a somewhat analogous situation.