This year marks a half-century since the discovery that a quantum field theory, now known as QCD (quantum chromodynamics), could be the underlying explanation for the strong nuclear force. That’s the force that holds quarks and gluons inside of protons and neutrons, and keeps protons and neutrons clumped together in atomic nuclei. This major step in theoretical physics occurred just a couple of years after it was discovered that a similar quantum field theory for the weak nuclear force (which includes W bosons, a Z boson and a Higgs boson) is mathematically consistent.
With these two breakthroughs came the sudden and unexpected triumph of quantum field theory, emerging as the basic mathematical and conceptual language for understanding the cosmos. It came after two decades in which most experts were convinced that quantum field theory was inconsistent, and only a stepping stone to something deeper.
This week I am in New York City attending two attached scientific meetings, both focused on QCD and other quantum field theories that share its key property, known as “confinement.” One meeting is hosted by New York University, and the other, the Annual Meeting of the Simons Collaboration on Confinement and QCD Strings, by the Simons Foundation. Many luminaries who have spent time on this subject are here together, ranging from David Gross, who co-invented the subject (and was a winner of the 2004 Nobel Prize), to brilliant graduate students who are hoping to reinvent it.
Why Does QCD Confine?
To say that “QCD confines” is to say that its force traps quarks and gluons inside particles such as protons and neutrons, collectively referred to as hadrons. [I have previously described this effect here, where I explain that it’s not quite true that a quark can’t ever come out of a proton, even though it can never be on its own.] But as I’ll describe in a moment, what’s really trapped, more fundamentally, are some of QCD’s own fields.
We physicists are all convinced that this is true. No quark or gluon has ever been observed outside a proton, neutron, or other hadron. Meanwhile, numerical simulations (known as “lattice QCD”, in which a tiny chunk of the cosmos is modeled in the computer as a small grid of points) show overwhelming evidence that quarks cannot exist on their own. Furthermore, we have a number of examples of theories with “supersymmetry” (more symmetry than that of QCD itself) in which there are multiple lines of mathematical evidence that quarks in those theories are confined. But no one can start with the math of QCD and prove, using mathematical and conceptual arguments alone without numerical simulation, that QCD predicts confinement.
Why The Electric Field and Electric Force Satisfy an Inverse Square Law
The mechanism of confinement is most easily explained by imagining a world slightly different from our own. It all goes back to an idea encountered already in first-year physics classes, known as Gauss’s law.
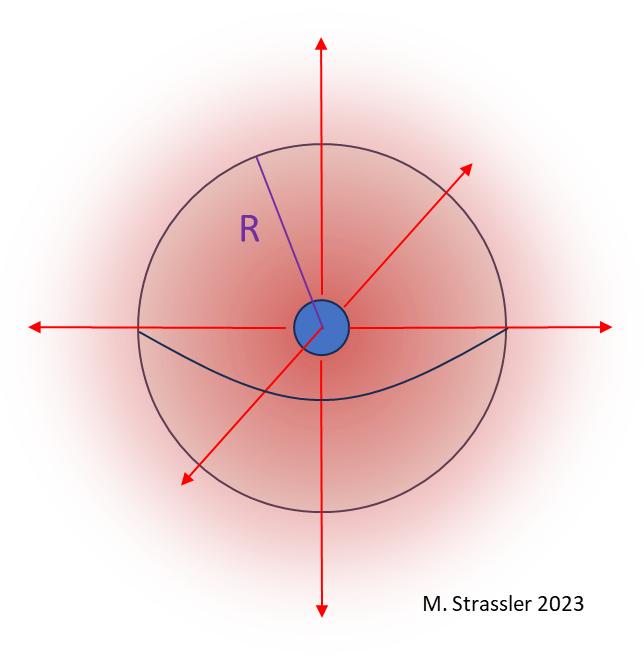
Gauss’s law explains why electrical forces satisfy an inverse square law — why, as the distance r between two electrically charged objects increases, the force between them declines as the square of the distance (F is proportional to 1/r2). The argument goes as follows: according to Gauss’s law, the electric field passing through a surface surrounding an electrically charged object, times the area of the surface where the field is non-zero, is proportional to the electric charge of that object. For instance, consider a ball of charge Q; its electric field will arrange itself in a spherically symmetric way, as illustrated in Figure 1. Now suppose we surround the ball with an imaginary sphere of radius R, and thus of surface area 4πR2. Then Gauss’s law states that the electric field passing through the imaginary surface is equal to the charge of the proton divided by the area of the imaginary sphere
- Electric field at the radius R equals Q / 4πR2
from which it immediately follows that if a charged object is at a distance r from the ball, the force exerted by the ball on that object falls as 1/r2.
If Electric Fields Confined
But now imagine that there were something about empty space that abhorred an non-zero electric field. More precisely, imagine that having a non-zero electric field anywhere in space would cost enormous amounts of energy. What would happen to the electric field around the ball? The field could not be zero, because then Gauss’s law would not be satisfied. On the other hand, its non-zero electric field would no longer spread out freely, because of the huge energy cost. What’s the poor field to do?
One possible answer: the field could form a narrow tube, as in Figure 2. We call this a flux tube. The existence of the tube still costs energy, but the cost is much smaller than if the non-zero field were spread out everywhere.
Let’s see what Gauss’s law says about this possibility. We can still draw an imaginary sphere as we did before, but across most of the sphere, the electric field is zero. Only where the tube intersects the sphere, in a region whose area equals the cross-sectional area A of the tube, would the electric field be non-zero. Thus Gauss’s law would then say
- Electric field within the tube at radius R equals Q / A
Since the cross-sectional area of the tube doesn’t depend on the size R of the imaginary sphere, the electric field in the tube doesn’t either — which means that an electrically-charged object inside the tube would feel a constant force, one that doesn’t decrease as the object moves away from the ball. Such an object could not ever escape from the ball, because no matter where it were placed, even many millions of miles away from the ball, an undiminished force would pull it back. This inability to escape is confinement.
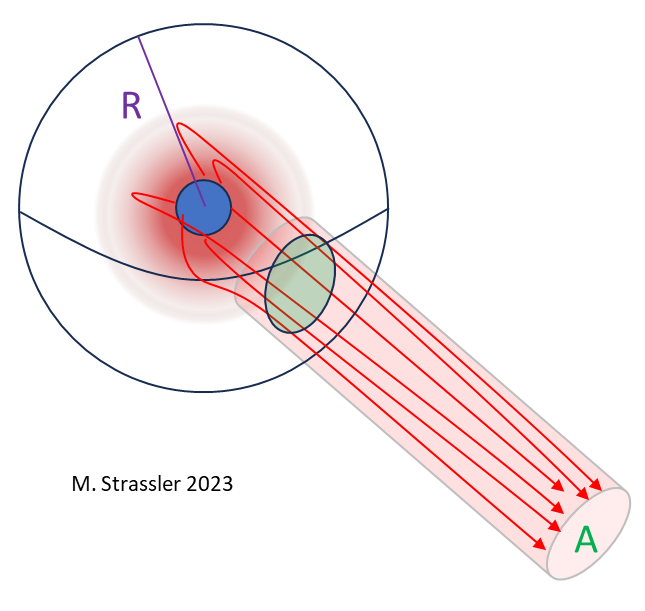
Importantly, what you see from Fig. 2 is that it is not just charged objects that are confined. What is really confined, first and foremost, is the non-zero electric field itself, trapped within a flux tube. The confinement of electrically charged objects is an automatic secondary consequence of this primary fact.
You might ask why the tube doesn’t collapse to zero size or expand to infinite size. The tube can’t grow too wide because that would increase the cost for energy space from the electric field’s presence. But it can’t become too narrow either, because the energy inside the tube grows like the square of the electric field. That means that there will always be some A for which these effects balance.
Confinement Happens in Nature, for Sure
The non-zero electric field found around electrons and protons most certainly isn’t confined. Nevertheless, confinement of other non-zero fields is observed in nature.
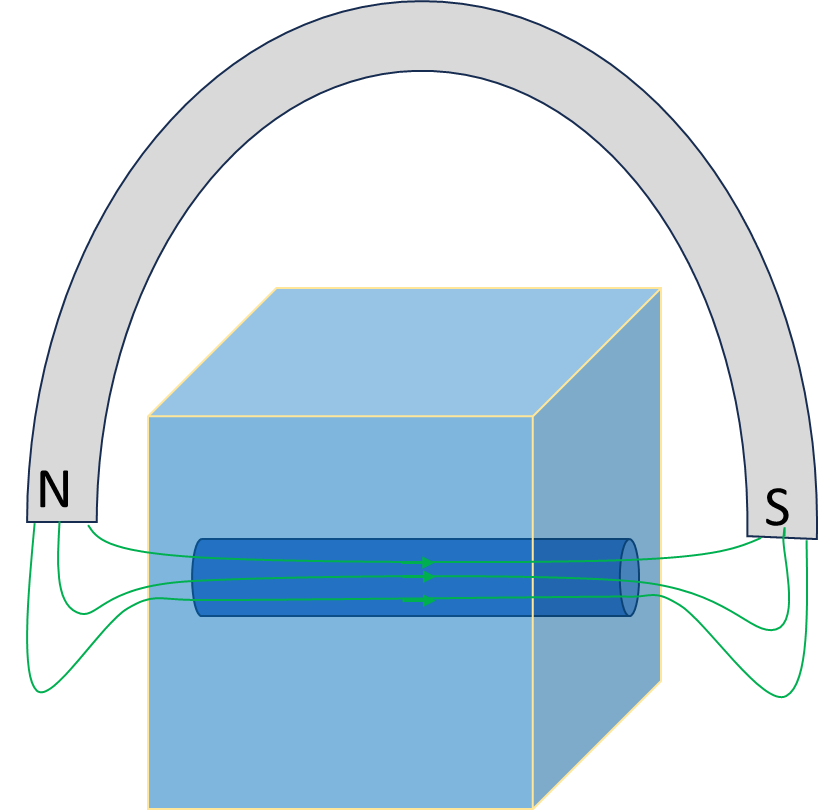
Non-zero magnetic field inside a Type II superconductor is confined; see Figure 3 for a rough illustration of such a flux tube inside a superconductor. These tubes, widely observed in experiments, are called “Abrikosov vortices”; Abrikosov was one of the awardees of the 2003 Nobel Prize. We do understand why a superconductor abhors the presence of a magnetic field; it’s a phenomenon known as the Meissner effect. [It is caused by the condensation of pairs of electrons known as Cooper pairs, which directly prevents a non-zero magnetic field from spreading out within the material of the superconductor.]
Meanwhile, the QCD analogue of the electric field, referred to as the chromo-electric field, is similarly confined into what are usually called QCD flux tubes or QCD strings. [I discussed the relation between QCD strings and string theory here; see especially Figures 3 and 4 of that post.] These tubes stretch between quarks, as in Figure 4, and that’s why quarks are confined. We can’t directly observe the flux tubes in experiments, as they’re far too short and thin, but there is considerable evidence for them. But we do not know exactly why they form — why empty space abhors a chromo-electric field. The fact that it does so has been dubbed a “Dual Meissner effect.” [Electric and magnetic fields are said to be related by “duality”, and so an effect that forces non-zero magnetic field into a tube is dual to one that has the same effect on non-zero electric field; the terminology has been extended to the chromo-electric field, as though empty space itself is a sort of dual chromo-superconductor.]

A proof that nonzero chromo-electric field must bind into tubes has remained elusive for fifty years. Not motivated? A million dollars goes to the clever person who figures it out. So get to work!



25 Responses
In the section “If electric fields confined” you state:
“But now imagine that there were something about empty space that abhorred an non-zero electric field.”
and
“The tube can’t grow too wide because that would increase the cost for energy space from the electric field’s presence.”
I was wondering what this energy cost for the electric field in empty space actually is, that balances the square of the electric field inside the tube. Is there a name for this effect?
There is an analogous effect, called the Meissner effect inside a superconductor, which abhors a non-zero magnetic field. Since electric currents can flow continuously without the addition of energy in a superconductor — the flow is, in a sense, frictionless — the presence of a magnetic field will cause current to spiral around the field lines, which in turn changes the magnetic field. The electric current will build up until the magnetic field in the material is canceled completely or trapped inside of tubes, called Abrikosov vortices.
Because the effect in question involves electric fields instead of magnetic fields, it is usually called the “dual Meissner effect” (reflecting a mathematical transformation that exchanges electric and magnetic effects and is called “electromagnetic duality”). The Meissner effect is caused by the free creation of electric current; the dual Meissner effect would presumably be caused by the free creation of magnetic current.
But where, you will then rightly ask, are the magnetic monopoles that carry the magnetic current, analogous to the electrons that carry electric current?! This is probably taking the analogy too far; there probably are no such objects. The magnetic currents are presumably an effect of the very strong forces that are found in QCD. Or perhaps even the idea of magnetic currents is taking the analogy too far. In any case, if anyone fully understood this top to bottom, they would be a million dollars richer: https://www.claymath.org/millennium/yang-mills-the-maths-gap/
I’m a bit confused about the “electric field flux tube” example. You make the statement that a charged particle wouldn’t be able to escape by traveling along the flux tube because the elecrtic field would be undiminished. But why couldn’t the charged particle move perpendicular to the flux tube, to get outside of it, where the electric field is zero (is it in this example?) In particular it seems like in the flux tube example, the electric field would be non-conservative, because the line integral along the path that goes from R to A along the flux tube, then leaves the flux tube, then goes back to A along a path outside of the flux tube, would be nonzero. Am I missing something here?
Fair question, as my explanation of this phenomenon is not complete. The point is that the flux tube emanating from the original particle has to end somewhere, on another particle; if not, the energy of the system is infinite.
If a QCD flux tube cannot break, then it must have ends, one on the quark I drew and one on an anti-quark that I did not draw. (See figure 3 of this post; note the valence quarks) If you try to move the quark and antiquark apart, the flux tube sticks to them; after all, it emerges from them. Without the quark, there’s no flux tube; and there is no quark without a flux tube emerging from it. This unbreakable connection (which follows from Gauss’s law, i.e. from gauge invariance) is why you cannot move the particle perpendicular to the flux tube — the tube is attached to it.
Real QCD flux tubes do break, because quarks have low mass; see this post. But you will see than even in this case, the quarks and anti-quarks can never be on their own; they’re always combined with other quarks and anti-quarks.
(The same ideas apply for gluons but they are a bit more subtle than I can cover right now.)
Matt, Can you explain how a numerical method Lattice QCD can show quark cannot exist by itself (confinement?). What happens numerically? Thanks.
The actual numerical method in a theory with no low-mass quarks is to take a ultra-high-mass stationary quark and a similar antiquark, place them a short distance apart, and separate them gradually. Thus, one measures the force (or really, the potential energy) as a function of the distance R between the quark and anti-quark. Linear growth of the energy with distance proves that moving the anti-quark infinitely far away, leaving the quark on its own, would require infinite energy. The flux tube between the quark and anti-quark can be observed, hence Figure 4.
When the theory has low-mass quarks as well, then the situation is more complicated because of the physics I described here. One only sees the flux tube in an intermediate regime where the quark and anti-quark are far enough apart to make a short tube but not so far apart that the tube snaps. Once the distance is large enough, a low-mass quark and its anti-quark are easily created from the vacuum, using the available energy in the tube; and these can attach themselves to the ultra-high-mass anti-quark and quark respectively, breaking the tube and reducing the energy between the quark and anti-quark to a finite value.
Since the latter case is the real world, strict “confinement of quarks”, as occurs in the former case, is an idealization that is not seen in nature. Real quarks can indeed be pulled out of protons, though they still never appear on their own, and indeed that’s why jets of hadrons form at the Large Hadron Collider. Nevertheless, confinement of flux seems to be true, though hard to prove and to demonstrate definitively even using lattice QCD.
“But we do not know exactly why they form — why empty space abhors a chromo-electric field.”
Schrodinger’s equation for an electron in a Hydrogen atom gives discrete, quantized energy gaps: how does one understand from this why empty space abhors continuous energy levels around a +q?
It’s not really related. Schrodinger’s equation is an approximation to quantum field theory, and it works quite well for an electron around a proton because electromagnetic forces are weak. But around a quark inside a proton, the strong nuclear force becomes very strong, and so Schrodinger’s equation simply doesn’t work. You need the full power of quantum field theory, as evidenced in the numerical simulations which lead to Figure 4. The whole system is far more complicated.
I should add — you still get discrete, quantized energy gaps: there’s a proton, then a Delta, then a whole host of other excited states. Or if you link a quark and an antiquark with a string, you get the pion, the rho, and then yet again a whole host of excited states of various energies and spins. But the calculation goes far beyond the Schroedinger equation.
If the solutions to Schrodinger’s equation didn’t require a physical interpretation as to why nature behaved this way at the time, then why do we need to understand why empty space abhors a chromo-electric field today via the solutions to QCD?
I suppose this is to do with the social dynamics of the physics community and how professional physicists within it have their different methods for interpreting and solving physics problems.
On the contrary: Schrodinger’s equation did most definitely require a physical interpretation. It requires that the electric field between an electron and a proton spreads out as in Figure 1, and is not confined into tubes as in Figure 2. The issue has nothing to do with social dynamics; it has to do with what electric fields in atoms actually do. (There was no need to worry about what chromo-electric fields do, since, within atoms, they are only relevant inside of protons and of neutrons.)
This artcle was very educational! I had sloppily thought of flux tubes as “strings” (no, not that theory) but this was so much more physically motivated.
Re superconductors it is true that they tend to display the Meisner effect, but to differing degree. Type II superconductors allow isolated field penetration. (Which by the way are not penetration by “tubes” but “vortices”.) But they all seem to rely on Cooper pairs, even though some condensation mechanisms may be “unconventional” (not lattice phonon driven).
I think the site filter rejects too short comments.
Spelling: Meissner.
An Abrikosov vortex IS a flux tube — it is both. It is a flux tube in that it contains magnetic field lines. It is a vortex in that the tube is maintained by flowing electric current on its outer surface — current that can flow freely since it is a superconductor. In fact, this fact is necessary by Ampere’s law! It would also be true of any solenoid in which current flows without resistance.
Do flux tubes have anything to do with quantum entanglement?
Again, I ask, could the flux tube cross-sectional area vary as in the Maxwell-Boltzmann distribution? I ask this because you mentioned the forces that are in play with confinement is the electric and magnetic, but what cause these fields?
So, if the vaccum ~ energy, then can you make the assumption that the fundamental mechanism could be “temperature”, i.e. the Maxwell–Boltzmann statistics? So, in the center of every massive particle there is a void, empty space, extremely cold because there are no particles due to the blockage created, inward flux is so high that it creates a wall of extremely high temperature hence creating the cold void in the center. So the “force” is derived from the conservation of energy, the hot particles/space tending to occupy the cold void.
Quantum entanglement isn’t a force (an interaction) but denotes correlations.
I thought we know from renormalization that QCD is asymptotically free, i.e. that the interaction strength increases with the distance. Why is that not enough to prove confinement?
Because what asymptotic freedom proves is that ***as long as the coupling constant is weak, one can confirm that it increases with distance.*** Once it becomes strong, one can prove nothing. There are plenty of asymptotically free theories that do *not* show confinement.
When you say “But no one can start with the math of QCD and prove” do you mean no one has so far or that there is a proof that it can’t be proven?
No one can prove it *yet*…
“Meanwhile, the QCD analogue of the electric field, referred to as the chromo-electric field, is similarly confined into what are usually called QCD flux tubes or QCD strings.”
So, can this thread of thinking be extended to gravity, (quantum gravity?)?
BTW: why do you assume the area of the flux tubes to be constant? Is that in line with the classic quantization approach to define quantum theory?
Could the flux tube cross-sectional area vary as in the Maxwell-Boltzmann distribution?
Tx.
Dr.Strassler:
The potential of an electric field goes KQ/R
The potential of the gravitational field goes GM/R
And it’s this characteristic that lets us “pull stuff apart” being held together by these fields that follow a 1/R^2 force law. Also, doesn’t this characteristic of 1/R^2 law keep the curl zero, which makes these fields conservative (path independent)
What would the potential of the strong force look like?
The constant force comes from a linear potential: energy is proportional to R. (Strictly speaking, in QCD the force is 1/R^2 at short distance and constant at long distance, so the potential goes from 1/R to R, with the cross-over at R of order R_proton. See for example https://www.researchgate.net/figure/The-heavy-quark-potential-in-lattice-units-The-short-distance-points-have-been_fig5_2028089 .
Figure 7, perhaps?
Really deserves another article.